Pada tahun 2018, kami mengadakan tiga kontes Yandex.Blitz - dalam pembelajaran mesin, pengembangan ponsel, dan front-end. Kompetisi ketiga diadakan baru - baru ini - selamat kepada para pemenang! Sementara itu, kami ingin kembali ke yang kedua, di mana tugas diusulkan di persimpangan algoritma dan perangkat lunak penulisan untuk Android / iOS. Calon untuk posisi pengembang seluler di Yandex akan mendapat manfaat dari pengalaman dalam memecahkan masalah tersebut. Baca analisis terperinci dari beberapa di antaranya. Dan jika Anda tidak berpartisipasi dalam Blitz, maka lebih baik untuk terlebih dahulu mencoba menyelesaikannya sendiri .

Tugas "pasokan gas"
| Masuk | Kesimpulan | Batas waktu | Batas memori |
|---|
| input standar atau input.txt | output standar atau output.txt | 15 detik | 15 megabita |
Nika sedang mengembangkan aplikasi untuk para manajer puncak di sebuah perusahaan gas besar untuk membantu mereka merencanakan produksi.
Perusahaan sedang mempertimbangkan bidang n yang d 1 ... d i ... d n kilometer jauhnya dari pipa dan dapat menghasilkan v 1 ... v i ... v n unit gas. Lisensi terpisah dijual untuk setiap bidang - lisensi adalah s 1 ... s i ... s n .
Untuk menghubungkan bidang dengan jalan raya, Anda perlu membangun jaringan pipa. Seorang kontraktor yang dapat meletakkan berbagai jenis pipa membantu perusahaan ini. Panjang pipa berbeda satu sama lain (l 1 ... l i ... l m ) dan harga (p 1 ... p i ... p m ). Mereka dapat digabungkan satu sama lain sesuka Anda.
Perusahaan memiliki koin k dan ingin mendapatkan gas sebanyak mungkin.
Berapa banyak yang dapat dihasilkan perusahaan jika memberikan pesanan optimal kepada kontraktor?
Pipa mungkin lebih panjang dari jarak dari lapangan ke pipa.
Baris pertama berisi bilangan bulat k ≤ 10 5 .
Baris kedua berisi bilangan bulat n ≤ 15.
Baris n berikutnya berisi tiga bilangan bulat d i ≤ 100, v i ≤ 100 dan s i ≤ 100.
Angka-angka dipisahkan oleh spasi.
Baris berikutnya berisi bilangan bulat m ≤ 15.
Baris m berikutnya berisi dua bilangan bulat l i ≤ 100 dan p i ≤ 100. Angka-angka dipisahkan oleh spasi.
Satu-satunya baris dengan jawabannya.
Contohnya
| Masuk | Kesimpulan |
116
3
58 7 50
81 71 56
52 57 31
3
47 9
1 25
18 61 | 57 |
Parsing
Untuk memulainya, mari kita tentukan notasi. Biarkan ada kelas objek Setoran (setoran) dengan parameter $ inline $ Dd_ {i} $ inline $ (keterpencilan) $ inline $ Dv_ {i} $ inline $ (volume produksi) dan $ inline $ Ds_ {i} $ inline $ (biaya lisensi). Objek indeks jenis ini akan menjadi variabel i. Ada juga kelas objek Pipeliner dengan parameter $ inline $ PPl_ {j} $ inline $ (panjang pipa yang dapat dibangun oleh kontraktor) dan $ inline $ PPp_ {j} $ inline $ (harga pipa ini), indeks melalui j. Para peserta blitz berkali-kali bertanya apakah satu jenis pipa dapat digunakan dua kali. Diasumsikan tidak, dan contoh ini jelas menunjukkan. Jadi dengan ketentuan tugas ini, menerima $ inline $ D_ {i} = {0, 1} $ inline $ (pilih bidang atau tidak) dan $ inline $ PP_ {j} = {0, 1} $ inline $ (pilih kontraktor atau tidak), Anda dapat membuat tugas pemrograman linier:
$ sebaris $ \ jumlah \ limit_ {i} D_ {i} * Dv_ {i} \ max rightarrow \\ \ jumlah \ limit_ {i} D_ {i} * Ds_ {i} + \ sum \ limit_ {j} PP_ { j} * PPp_ {j} \ leq k \\ \ jumlah \ limit_ {i} D_ {i} * Dd_ {i} \ leq \ jumlah \ limit_ {j} PP_ {j} * PPl_ {j} \\ D_ { i} = {0, 1}, PP_ {j} = {0, 1} $ inline $
Ini dapat diselesaikan, misalnya, dengan metode simpleks. Namun, berdasarkan ketentuan tugas, kami diharuskan untuk mengembalikan hanya volume produksi maksimum (yaitu, nilai fungsi tujuan) dan tidak diharuskan untuk menunjukkan bidang mana dan kontraktor mana yang harus dipilih. Bersama dengan pembatasan dalam kondisi tersebut, masalahnya dapat diselesaikan dengan metode pemrograman dinamis dengan membangun tabel dp [panjang] [uang], di mana panjang adalah panjang pipa, uang adalah uang. Setelah konstruksi tabel yang benar, cukup untuk menemukan nilai maksimum di dalamnya, yang akan menjadi jawabannya. Kendala memori tugas cukup untuk membangun.
Tugas "Menara dan AI"
| Masuk | Kesimpulan | Batas waktu | Batas memori |
|---|
| input standar atau input.txt | output standar atau output.txt | 1 detik | 64 megabita |
Artem mengembangkan kecerdasan buatan memainkan game mobile yang kompetitif. Aturan mainnya sederhana.
Sebelum para pemain ada n menara dengan ketinggian c 1 ... c i ... c n . Pada gilirannya, pemain dapat memecahkan salah satu menara sehingga diperoleh beberapa menara yang lebih kecil. Pemain takut menjadi bingung di menara, sehingga mereka menyetujui batasan: setelah pemisahan, dua menara dengan ketinggian yang sama tidak boleh diperoleh. Misalnya, menara dengan ketinggian 7 dapat dibagi menjadi (1, 2, 4), tetapi tidak menjadi (1, 3, 3). Tinggi selalu bilangan bulat.
Kehilangan orang yang tidak memiliki menara yang bisa dihancurkan.
Artem memiliki teman yang sangat cerdas yang bermain optimal - dengan kecerdasan artifisial Artemlah yang berjuang. Untuk mengevaluasi pekerjaan AI, Artyom perlu tahu apakah robot harus menang jika kedua pemain bertindak optimal. Bantu dia dengan ini.
Manusia selalu berjalan dulu. Dia akan bermain dengan game AI k.
Baris pertama berisi bilangan bulat k <500.
Ini diikuti oleh k blok dari dua garis.
Baris pertama dari setiap blok adalah bilangan bulat 0 <n ≤ 50.
Baris kedua dari setiap blok memiliki n bilangan bulat 0 <c i ≤ 50. Angka-angka dipisahkan oleh spasi.
k baris, yang masing-masing berisi benar atau salah, tergantung pada apakah seseorang memenangkan permainan.
Contohnya
| Masuk | Kesimpulan |
2
1
4
2
1 1 | salah
salah |
Parsing
Game menara yang diusulkan adalah permainan akhir yang adil untuk dua pemain di mana tidak mungkin untuk menggambar.
Oleh karena itu, kemenangan pemain tertentu dalam permainan ditentukan oleh kondisi permainan dan urutan gerakan kedua pemain. Bagi pembaca yang terbiasa dengan teori permainan, jelas bahwa salah satu permainan yang sama dari dua pemain sebenarnya setara dengan permainan "dia", yang berarti permainan kami juga.
Berikut ini adalah deskripsi singkat tentang dia-sebuah game ( tautan ke sumber - klik di atasnya untuk ulasan terperinci):
Ada beberapa tumpukan, masing-masing memiliki beberapa batu. Dalam satu gerakan, pemain dapat mengambil jumlah batu yang tidak nol dari satu tumpukan dan membuangnya. Karenanya, kerugian terjadi ketika tidak ada lagi gerakan yang tersisa, mis. semua tumpukan kosong.
Jadi, keadaan permainan "dia" secara unik dijelaskan oleh satu set bilangan alami yang tidak teratur. Dalam satu gerakan, itu diperbolehkan untuk secara ketat mengurangi salah satu angka (jika sebagai hasilnya angka menjadi nol, maka akan dihapus dari set).
Solusi untuk permainan nim adalah menemukan jumlah xor dari ukuran tumpukan, dan hanya jika jumlah ini bukan nol, kita dapat dengan jelas menyatakan bahwa kita berada dalam keadaan menang.
Lebih lanjut, teorema Sprag-Grandi datang ke bantuan kami, yang menyatakan bahwa status U dari setiap permainan yang sama dari dua pemain dapat dikaitkan dengan segelintirnya-permainan ukuran X. Segera setelah fungsi yang menentukan pemetaan keadaan permainan kami kepadanya adalah sebuah permainan, solusi untuk masalahnya akan berkurang untuk menyelesaikannya - game yang sudah dikenal.
Tugas “Indikasi Penilaian”
| Masuk | Kesimpulan | Batas waktu | Batas memori |
|---|
| input standar atau input.txt | output standar atau output.txt | 1 detik | 64 megabita |
Galya sedang mengembangkan agregator peninjauan. Dia memutuskan untuk menunjuk peringkat lembaga dengan bantuan bintang berujung tujuh.
Sistem rendering input menerima persegi panjang tinggi h dan lebar w, sudut kiri atas yang terletak di titik (x, y). Bintang harus ditarik sesuai dengan aturan berikut:
- Ukuran bintang ditentukan oleh lebar atau tinggi persegi panjang - yaitu lebih kecil. (Lihat gambar.)
- Jika salah satu dimensi dari persegi panjang lebih besar dari dimensi yang sesuai dari bintang, bintang harus dipusatkan pada dimensi itu.
- Bintang itu menunjuk ke atas.
Sistem rendering mengharapkan koordinat simpul bintang dari kode Gali. Bantu Gale untuk menghitungnya.
Untuk membangun bintang berujung tujuh, Galya mengambil garis luar sosok yang diperoleh dengan menghubungkan simpul heptagon biasa melalui satu. Dalam sistem koordinat, sumbu X diarahkan dari kiri ke kanan, sumbu Y dari atas ke bawah. Program Gali tidak crash, menerima nilai lebar dan tinggi yang salah sebagai input.
Satu baris berisi bilangan bulat x, y, w dan h, dipisahkan oleh spasi.
Contoh: entri 150 0 50 100 menunjukkan persegi panjang dengan lebar 50 poin, tinggi 100 poin dan dengan sudut kiri atas pada titik (150, 0).
Satu-satunya garis yang berisi 28 angka yang dipisahkan oleh spasi adalah koordinat simpul bintang, mulai dari atas dan kemudian searah jarum jam. Angka harus dibulatkan ke bilangan bulat terdekat. Lihat contoh output dan ilustrasi masalah sebelum melanjutkan dengan solusi.
Contoh: output dari tiga titik (1, 2), (3, 4), (5, 6) akan terlihat seperti ini: 1 2 3 4 5 6.
Contohnya
| Masuk | Kesimpulan |
0 0 100 100 | 50 1 65 21 90 21 85 45 100 64 78 75 72 99 50 88 28 99 22 75 0 64 15 45 10 21 35 21 |
Catatan
Akurasi yang diperlukan adalah 10 digit signifikan.
Sistem koordinat: Sumbu X diarahkan dari kiri ke kanan, Sumbu Y dari atas ke bawah:
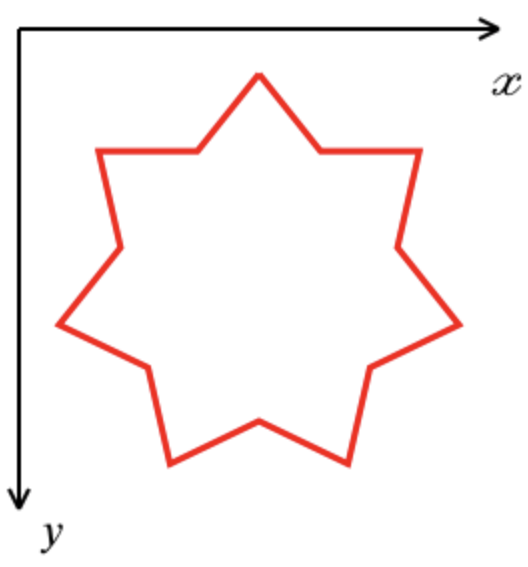
- Urutan vertex yang diharapkan:
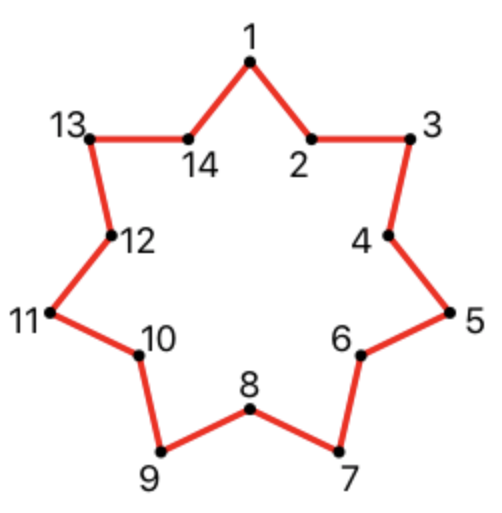
Contoh bintang bertulis:
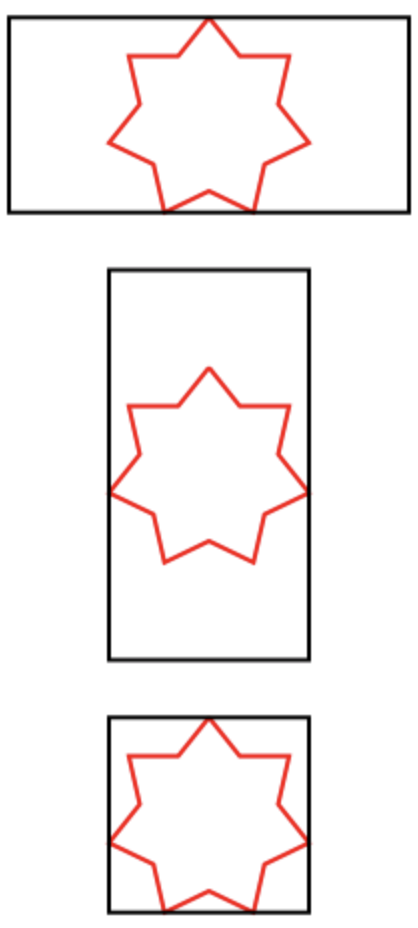
Parsing
Solusi untuk masalah ini dikurangi menjadi tiga tahap: untuk membangun bintang referensi dengan orientasi yang diinginkan dalam ruang, skala poin yang dihasilkan, menghitung dan menerapkan offset.
Membangun bintang
Cara termudah adalah dengan membangun bintang bertuliskan dalam lingkaran dengan jari-jari satuan berpusat di titik asal. Titik-titik simpul eksternal dihitung menggunakan trigonometri trivial, tetapi dengan yang internal tugasnya sedikit lebih rumit. Mereka dapat ditemukan setidaknya dalam dua cara. Cara yang lebih mudah adalah dengan menemukan persimpangan segmen yang menghubungkan simpul luar. Yang lebih rumit adalah menemukan rumus untuk menghitung jari-jari lingkaran bertulis dari jari-jari lingkaran terbatas. Cara termudah untuk melakukan ini adalah pertama, misalnya, untuk bintang berujung 5, dan digeneralisasikan ke bintang berujung N dengan celah sembarang antara simpul yang terhubung.
Scaling
Dalam semua kasus, ukuran diberikan di mana kita perlu menyesuaikan bintang. Jadi, kita perlu mengukur titik yang diperoleh sehingga jarak dari kiri ke kanan tidak melebihi lebar yang ditentukan, dan jarak dari tertinggi ke terendah tidak melebihi ketinggian yang ditentukan. Kami mengambil faktor penskalaan untuk membawa lebar dan tinggi ke nilai yang diinginkan, dan pilih yang lebih kecil. Karena kami dengan hati-hati membangun bintang referensi dengan pusat di titik asal, cukup dengan mengalikan koordinat dari setiap titik dengan koefisien yang dipilih.
Offset
Hal terakhir yang tersisa adalah memindahkan titik kami sehingga bintang berada dalam bingkai yang diberikan. Data input semua opsi dapat direduksi menjadi kotak pembatas dengan koordinat yang diberikan dari sudut kiri atas. Semuanya sederhana di sini: kita mengambil titik tertinggi dari hasil yang diperoleh pada tahap terakhir, mempertimbangkan perbedaan koordinat y dengan koordinat y dari sudut kiri atas, dan menggeser semua poin secara vertikal dengan nilai yang diperoleh. Kami melakukan hal yang sama dengan koordinat x, hanya mengambil bukan titik paling atas, tetapi yang paling kiri. Ada satu sentuhan terakhir: pusatkan bintang pada persegi panjang ini.
Tindakan lebih lanjut tergantung pada koefisien apa yang kami pilih pada tahap sebelumnya:
- jika diskalakan pada ketinggian - kita mengambil perbedaan antara lebar persegi panjang dan jarak dari kiri ke titik paling kanan;
- jika diberi skala lebar - kita mengambil perbedaan antara tinggi persegi panjang dan jarak dari titik tertinggi ke titik terendah.
Bagilah nilai yang diperoleh dengan 2 dan geser titik sesuai dengan pengukuran yang sesuai. Jawaban diterima.
Tugas "Rotasi dan penskalaan lingkaran"
| Masuk | Kesimpulan | Batas waktu | Batas memori |
|---|
| input standar atau input.txt | output standar atau output.txt | 1 detik | 64 megabita |
Vika sedang mengembangkan editor grafis untuk smartphone dan tablet. Dia ingin memberi pengguna kesempatan untuk memutar lingkaran di layar dengan dua jari dan mengubah ukurannya, seperti ini:
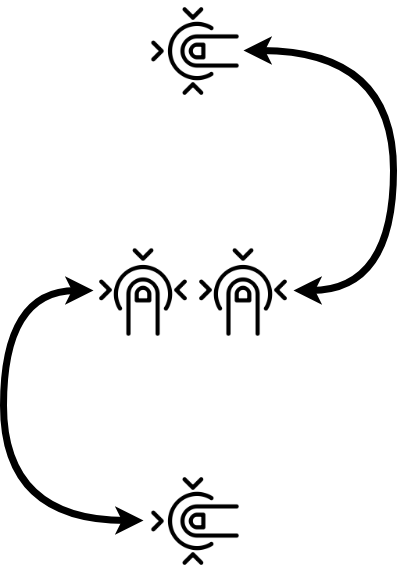
Angka tersebut berputar pada sudut yang sama dengan ruas yang menghubungkan jari-jari berputar. Ukuran gambar berubah proporsional dengan panjang segmen. Pertama, gambar diputar, dan kemudian ukurannya diubah. Awalnya, lingkaran memiliki koordinat (x, y) dan jari-jari r. Daftar acara sentuh yang menggambarkan gerakan pengguna diberikan. Bantu Vika menghitung koordinat akhir dari pusat lingkaran dan jari-jarinya. Lingkaran berputar relatif ke titik (a, b).
Deskripsi acara sentuh berisi id jari, koordinat dan jenis acara. Jari pertama yang dilampirkan pengguna menerima id 0, yang kedua - id 1, dan seterusnya.
Contoh:
0 337 490 ACTION_DOWN - ini berarti bahwa dengan jari 0 pada titik (337, 490) peristiwa ACTION_DOWN terjadi.
Acara sentuh adalah dari jenis berikut:
- ACTION_DOWN - pengguna menerapkan jari pertama ke layar pada titik tertentu.
- ACTION_POINTER_DOWN - pengguna menerapkan jari kedua ke layar pada titik tertentu.
- ACTION_MOVE - pengguna telah menggerakkan jarinya ke titik tertentu.
- ACTION_POINTER_UP - pengguna memindahkan jari kedua ke titik yang ditentukan dan melepaskannya.
- ACTION_UP - pengguna memindahkan jari pertama ke titik yang ditentukan dan melepaskannya.
- ACTION_CANCEL - gerakan yang dibatalkan pengguna.
Baris pertama berisi angka x, y, dan r, dipisahkan oleh spasi. Baris kedua berisi angka a dan b, dipisahkan oleh spasi. Beberapa baris berikutnya berisi acara sentuhan berurutan.
Satu-satunya garis dengan koordinat dan jari-jari. Angka dipisahkan oleh spasi.
Contoh
| Masuk | Kesimpulan |
252 194 78
445.559
0 337.490 ACTION_DOWN
1.599.490 ACTION_POINTER_DOWN
1.576.564 ACTION_MOVE
1.552.590 ACTION_MOVE
0 407.375 ACTION_MOVE
1 505 615 ACTION_MOVE
1 482 620 ACTION_MOVE
0 477 360 ACTION_MOVE
1.435.616 ACTION_MOVE
1.411.607 ACTION_MOVE
0 547 386 ACTION_MOVE
1 364 548 ACTION_POINTER_UP
0 571 387 ACTION_UP | 831 704 73 |
Catatan
Saat menampilkan hasilnya, perlu untuk membulatkan semua nilai floating-point ke nilai integer sesuai dengan aturan pembulatan matematika.
Parsing
Terlepas dari kenyataan bahwa gerakan itu tampak rumit, ia dapat dibagi menjadi dua komponen: rotasi dan penskalaan. Untuk memutar angka, kita perlu menghitung sudut rotasi, yang dapat diperoleh dengan menggunakan rumus berikut:
a = atan2 (prevTouchX2 - prevTouchX1, prevTouchY2 - prevTouchY1) - atan2 (currentTouchX2 - currentTouchX1, currentTouchY2 - currentTouchY1).
Setelah menerima sudut rotasi, Anda perlu memutar gambar itu sendiri, yang mengurangi untuk mengubah setiap titik gambar dengan sudut rotasi. Setelah kami memutar angka, kita perlu skala itu. Menskalakan angka cukup sepele. Penting untuk mengingat jarak antara jari pertama dan kedua saat menerima acara ACTION_POINTER_DOWN untuk jari kedua, setelah itu, dengan melacak jarak antara dua jari pertama, Anda dapat menghitung koefisien yang digunakan untuk mengukur skala gambar.
Tugas "Konstruksi Jalan"
| Masuk | Kesimpulan | Batas waktu | Batas memori |
|---|
| input standar atau input.txt | output standar atau output.txt | 1 detik | 64 megabita |
Dalam gim seluler, karakter utama membangun basis di planet yang jauh. Dia mulai dengan perimeter - menara yang dihubungkan oleh dinding laser langsung. Arsitek dari kantor pusat mengiriminya sebuah rencana yang menunjukkan n menara dengan koordinat (x 1 , y 1 ) ... (x i , y i ) ... (x n , y n ). Dari sudut pandang pertahanan dasar, tidak masuk akal untuk menempatkan tiga atau lebih menara tetangga pada satu garis lurus. Arsitek staf, kadang-kadang, memposisikan menara dengan cara ini, sehingga pemain sendiri harus menghapus menara perantara tambahan.
Setelah selesai dengan perimeter, sang pahlawan mulai melengkapi pangkalan dari dalam. Dia ingin membangun jalan k antara menara - jalan dapat menghubungkan dua menara yang tidak berdekatan, tetapi tidak dapat melintasi jalan atau dinding lain. Sebanyak jalan yang Anda inginkan dapat keluar dari satu menara.
Pahlawan memiliki robot jalan p. Untuk memilih rencana pembangunan jalan yang optimal, pahlawan memerintahkan mereka untuk memilah-milah semua opsi yang mungkin. Robot mulai bekerja secara simultan dan berulang-ulang pada saat yang sama membawa opsi unik untuk lokasi jalan. Jika sebelum iterasi berikutnya ternyata ada pilihan yang lebih sedikit daripada robot, maka robot ekstra dibebaskan dan dikirim ke dapur untuk memasak makan malam. Robot yang tersisa menyelesaikan opsi terakhir dan mematikan.
Jika ternyata Anda dapat membuka jalan di luar pangkalan, pahlawan menyatakan pangkalan tidak aman dan terbang menjauh dari planet ini.
Berapa banyak robot yang akan bekerja di dapur?
Baris pertama berisi tiga bilangan bulat 4 ≤ n ≤ 10 7 , 1 ≤ k ≤ n dan bilangan prima 105 <p <11 × 104. Angka-angka dipisahkan oleh spasi.
N baris berikutnya berisi dua bilangan bulat 0 <x i , y i <109. Angka-angka dipisahkan oleh spasi.
Satu-satunya baris dengan jawabannya. Jika pangkalan tidak aman, cetak −1.
Contoh 1
| Masuk | Kesimpulan |
4 1 101363
0 0
1 0
1 1
0 1 | 101361 |
Ada dua cara untuk membuka satu-satunya jalan: (0, 0) - (1, 1) dan (1, 0) - (0, 1). Dua robot akan terlibat di dalamnya, dan sisanya akan pergi ke dapur: p - 2 = 101 361.
Contoh 2
| Masuk | Kesimpulan |
4 1 101363
1 0
2 0
0 1
1 2 | -1 |
Di sini Anda dapat membangun jalan antara (1, 0) - (0, 1), dan ini berada di luar pangkalan. Pahlawan mengenali markas sebagai tidak aman, jawabannya adalah −1.
Contoh 3
| Masuk | Kesimpulan |
4 1 101363
0 0
1 0
2 0
0 1 | 101363 |
Menara (0, 0), (1, 0) dan (2, 0) berada di garis yang sama, sehingga pahlawan tidak akan membangun menara tengah (1, 0). Tidak ada jalan yang bisa diaspal, oleh karena itu, semua robot akan segera pergi ke dapur: p = 101 363.
Parsing
Kami membagi solusi masalah menjadi tiga langkah.
Langkah pertama adalah menentukan untuk input data vertex mengatur apakah poligonnya cembung, dan jika demikian, berapa banyak simpul nyata yang dimilikinya. Poligon adalah cembung jika semua simpulnya terletak di satu sisi garis yang mendukung setiap tepi. Untuk setiap triple dari simpul yang berdekatan $ sebaris $ (x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1}) $ inline $ membangun beberapa vektor $ inline $ ab = ((x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i})) dan bc = ((x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1})) $ inline $ , dan hitung tanda ekspresi ab.x bc.y - bc.x ab.y. Jika ekspresi adalah 0, maka simpul terletak pada satu garis lurus dan, sesuai dengan kondisi masalah, menara yang berdiri di simpul tengah menghilang, mengurangi jumlah total menara. Jika untuk semua tiga kali lipat simpul tanda produk adalah 0 atau selalu sama, maka lanjutkan ke langkah kedua, jika tidak, kami menganggap basis tidak aman dan mencetak jawaban -1.
Langkah kedua. Jumlah cara untuk membangun k disjoint diagonal di dalam cembung N-gon adalah $ inline $ V = 1 / (k + 1) {N-3 \ pilih k} {N + k-1 \ pilih k} $ inline $ , tetapi kita perlu menghitung ekspresi p - V mod p, di mana p adalah bilangan prima.
Bayangkan N! bagaimana $ inline $ a * p ^ e $ inline $ , di mana faktor umum terbesar adalah a, dan p gcd (a, p) = 1.
$ sebaris $ {n \ pilih r} = (n!) / (r! (nr)!) = a_ {1} * p ^ {e_ {1}} / a_ {2} * p ^ {e_ {2} } * a_ {3} * p ^ {e_ {3}} = (a_ {1} / a_ {2} * a_ {3}) * p ^ {e_ {1} -e_ {2} -e_ {3} } $ inline $
Jika $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ inline $ , maka ekspresi dapat dibagi oleh p dan jawaban dalam masalah adalah p.
Untuk kasus $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ inline $ = 0 jawabannya adalah $ inline $ a_ {1} / a_ {2} * a_ {3} $ inline $ mod p.
Dalam perhitungan, kami memperhitungkan bahwa b mod p = (a mod p) (b mod p) mod p, dan $ inline $ k ^ {- 1} $ inline $ mod p = $ inline $ (k) ^ {p-2} $ inline $ mod p untuk prime p.
Langkah ketiga. Untuk menghitung ekspresi $ inline $ e_ {1} -e_ {2} -e_ {3} $ inline $ bayangkan n! sebagai 1 2 ... p (p + 1) ... 2p (2p + 1) ..., sedangkan (p + 1) ... (2p-1) mod p = 1 2 ... (p-1 ) = (p-1)! .. Total, n mod p = ( $ inline $ (p-1)! ^ k $ inline $ k (n mod p)!) mod p, di mana k = lantai (n / p).
Tugas “Penjadwal Super Sederhana”
| Masuk | Kesimpulan | Batas waktu | Batas memori |
|---|
| input standar atau input.txt | output standar atau output.txt | 10 detik | 224 megabyte |
Ada n tugas yang harus dilakukan pada prosesor smartphone. Implementasinya membutuhkan t 1 ... t i ... t n satuan waktu, dan pada awal satuan ke-i, tugas ke-i harus diselesaikan.
Agar tepat waktu, tugas dapat dilakukan dalam beberapa utas, namun, setiap utas baru menghasilkan beban yang meningkat pada baterai. Pada aliran pertama, satu unit energi dikonsumsi per satuan waktu, pada yang kedua setengah unit energi, pada yang ketiga setengah kali lebih banyak dari pada yang kedua, dll.
Tugas dapat dibagi menjadi unit waktu: pertama, sebagian selesai, kemudian beralih ke yang lain, lalu kembali ke yang pertama. Anda tidak dapat melakukan tugas yang berbeda di utas yang berbeda secara bersamaan.
Penjadwal menerima tugas satu per satu; Setelah menerima tugas, ia segera mengalokasikan slot waktu untuk itu. Setelah tugas didistribusikan, penjadwal tidak dapat mentransfernya ke slot lain.
Berapa banyak energi yang dibutuhkan untuk menyelesaikan semua tugas jika didistribusikan secara optimal?
Baris pertama berisi bilangan bulat 1 <n ≤ 3 × 10 3 .
Baris n berikutnya berisi dua bilangan bulat 0 ≤ t i ≤ 10 4 dan 0 ≤ d i ≤ 10 4 . Angka dipisahkan oleh spasi.
Satu-satunya baris dengan jawabannya. Akurasi - delapan tempat desimal.
Contoh
| Masuk | Kesimpulan |
5
2 2
1 1
3 4
1 10
1 2 | 10.25000000 |
Parsing
Karena, sesuai dengan kondisi masalah, cukup bagi kita untuk menghitung hanya jumlah energi yang dikonsumsi, kita dapat menggunakan metode solusi dengan menghitung jumlah energi yang dikonsumsi untuk setiap unit waktu. Ketika merencanakan tugas, kami mengambil nilai minimum dari energi yang dikonsumsi k = 1 dan, mulai dari batas waktu tugas, kami memilah-milah semua slot interval waktu.
Jika konsumsi energi slot kurang dari koefisien (k) dan slot waktu ini tidak digunakan saat merencanakan tugas, maka kami menempati slot ini untuk menyelesaikan tugas dengan meningkatkan koefisien slot oleh K. Ketika kami mencapai awal periode waktu, kita perlu meningkatkan koefisien k sebesar 1,5 kali dan ulangi pencarian slot waktu, mulai dari tenggat waktu dan hingga tugas sepenuhnya direncanakan. Setelah menyelesaikan perencanaan semua tugas, hanya menghitung konsumsi energi total dengan menambahkan koefisien yang diperoleh dari setiap unit waktu.
Tugas Objek Destructible
| Masuk | Kesimpulan | Batas waktu | Batas memori |
|---|
| input standar atau input.txt | output standar atau output.txt | 2 detik | 64 megabita |
2D- . , : n- (x 1 , y 1 )...(x i , y i )...(x n , y n ). — , . . , — , .
, [0 1 2 3 4], 1 3 1 3, [1 2 3] [0 1 3 4].
, . . , , .
, ?
n ≤ 500. n x y. .
. — .
Contoh 1
| Kesimpulan |
4
100 100
200 100
200 200
100 200 | 0.000000 |
Contoh 2
| Kesimpulan |
6
167 84
421 84
283 192
433 298
164 275
320 133 | 326.986753 |
, , . « » : — . : , ( ) .
, ? ( , , ). : , , , . , , ( ) . even-odd rule: . — , ( ) , — .
, , — , . (, , ):
- ( );
- : , - ;
- ( , 10-5 );
- even-odd rule — ;
- : 180 .
«DNA»
| Kesimpulan | | |
|---|
| input.txt | output.txt | 8 | 128 |
, . , , . n . , . : A, T, G C. . .
n. n . . 6⋅10 6 .
. . . . . , .
( , ):
5
TTT
GAAGCT
CAAT
AGA
AGGCA
:
2 TTT
6 AGA
28 AGA
30 AGA
57 CAAT
86 AGA
100 GAAGCT
190 TTT
191 TTT
196 AGA
219 TTT
232 AGA
271 TTT
284 TTT
285 TTT
298 TTT
320 TTT
330 TTT
331 TTT
342 TTT
373 AGA
397 AGA
488 AGA
509 AGA
524 AGA
565 TTT
574 AGA
605 AGA
625 CAAT
630 AGA
681 CAAT
718 TTT
719 TTT
744 AGGCA
754 AGA
784 AGA
808 TTT
821 CAAT
833 AGA
861 CAAT
879 AGA
921 AGA
955 AGA
, . — , — . , . . , .
, .
«QR Quest»
| Kesimpulan | | |
|---|
| input.txt | output.txt | 1 | 64 |

t, . t n i , .
t , .
Contoh 1
| Kesimpulan |
4
8 10 1 9 2 6 7 8
14 2 0 11 10 4 1 0
6 6 4 1 10 0 11 6
11 4 3 4 14 8 12 5 | 0
13
15
5 |
Contoh 2
| Kesimpulan |
4
9 10 6 2 12 11 7 2
3 10 1 14 13 13 1 1
6 8 8 5 3 2 6 4
5 11 5 5 3 1 10 7 | 3
9
2
7 |
, . QR- , . - .
Total delapan angka dimasukkan - koordinat sel dalam tabel ini, yaitu 4 pasang dengan koordinat kolom dan baris. Itu perlu untuk menebak operasi apa yang dilakukan dengan sel-sel ini dan dari tabel mana sel tambahan.
Dengan menggunakan manipulasi sederhana, orang dapat memverifikasi bahwa ini adalah xor-sum untuk empat sel tabel A, B, dan C, yang dialamatkan oleh indeks a 0 ... a 7 :
R = A [a 0 , a 1 ] ^ B [a 2 , a 3 ] ^ B [a 4 , a 5 ] ^ C [a 6 , a 7 ].