Bukti tempat di mana simetri tidak bisa ada

Prestasi matematika utama adalah hipotesis Zimmer yang ditemukan oleh tim peneliti yang kecil.

Untuk kisi-kisi dalam dimensi simetri yang lebih tinggi, tidak selalu mungkin untuk mentransfer ke dimensi di bawah peringkat

Keberhasilan Robert Zimmer dapat didefinisikan dalam banyak hal. Sebagai presiden Universitas Chicago sejak 2006, ia menjadi berita utama, menemukan jumlah sembilan angka untuk pendanaan dan menerbitkan artikel untuk mendukung kebebasan berbicara di kampus. Tetapi sebelum menjadi presiden universitas, ia adalah seorang ahli matematika. Dan lama setelah dia meninggalkan penelitian serius, rencana penelitian yang dia luncurkan akhirnya memberikan hasil.

Setahun yang lalu, tiga matematikawan membuktikan hipotesis Zimmer terkait dengan keadaan di mana ruang geometris memiliki simetri dari jenis tertentu. Bukti mereka telah menjadi salah satu pencapaian matematika terbesar dalam beberapa tahun terakhir. Ini mengakhiri pertanyaan yang muncul sebelum Zimmer selama aktivitas mentalnya yang intens pada akhir 1970-an dan awal 1980-an.

"Saya akan mengatakan bahwa saya pergi tidur selama lima tahun dengan memikirkan tugas ini, setiap malam, jadi saya terobsesi dengan hal itu, dan sangat menyenangkan untuk menyaksikan bagaimana orang menyelesaikannya," kata Zimmer.

Biasanya, semakin besar ruang dimensi geometris, semakin banyak simetri di dalamnya. Ini bisa dibayangkan dengan mempelajari lingkaran yang ada pada bidang dua dimensi dan bola memanjang dalam tiga dimensi: ada lebih banyak cara untuk memutar bola daripada ada cara untuk memutar lingkaran. Dimensi bola tambahan membuat simetri tambahan.

Dugaan Zimmer mengacu pada simetri dari jenis khusus yang dikenal sebagai kisi tingkat tinggi. Dia bertanya apakah pengukuran ruang geometris membatasi penggunaan simetri jenis ini. Para penulis karya baru - Aaron Brown dan Sebastian Hurtado-Salazar dari University of Chicago dan David Fisher dari Indiana University - menunjukkan bahwa dengan jumlah pengukuran yang kurang dari simetri spesifik tertentu tidak diamati. Dengan demikian, mereka membuktikan kebenaran hipotesis Zimmer.


Robert Zimmer, sekarang presiden Universitas Chicago, mengembangkan hipotesis yang dinamai menurut namanya hampir 40 tahun yang lalu

Pekerjaan mereka menjawab satu pertanyaan penting dan lama, membuka cara-cara baru untuk mempelajari banyak hal lain. Ini juga mengungkapkan sifat intrinsik ruang geometris. Simetri adalah salah satu sifat paling sederhana dari ruang tersebut. Karya baru mengatakan bahwa simetri bisa ada di ruang-ruang dari satu jenis, dan tidak bisa di yang lain. Prestasi ini dicapai setelah beberapa dekade downtime.

"Hipotesanya terlihat seperti itu bisa membuat orang sibuk untuk waktu yang sangat lama," kata Amy Wilkinson, seorang ahli matematika di University of Chicago, yang menyelenggarakan konferensi tahun ini pada bukti ini. "Dan mereka secara relatif menghancurkan pertanyaan ini."

Simetri yang memuaskan

Simetri adalah salah satu konsep geometris pertama yang ditemukan anak-anak dalam matematika. Dengan tangan mereka sendiri, mereka belajar bahwa Anda dapat memutar, membalik dan menggeser formulir, dan pada akhirnya mendapatkan bentuk yang sama dengan yang mereka mulai. Mempertahankan bentuk objek sebagai hasil dari perubahan merespons dengan kepuasan internal tertentu - ini adalah petunjuk dari tatanan yang lebih dalam di Alam Semesta.

Matematikawan memiliki bahasa formal mereka sendiri untuk mempelajari simetri. Ini memberi mereka kesempatan untuk berdiskusi secara ringkas tentang berbagai simetri yang berlaku dalam ruang geometris tertentu.

Sebuah kotak, misalnya, memiliki delapan simetri - delapan cara untuk membalik atau memutarnya, kembali mendapatkan kotak. Lingkaran dapat diputar berapa pun derajatnya; dia memiliki jumlah simetri yang tak terbatas. Matematikawan mengumpulkan semua simetri objek geometris yang diberikan, atau ruang, dan mengemasnya menjadi "kelompok".

Grup menarik dengan sendirinya. Mereka sering muncul sebagai hasil dari mempelajari ruang geometrik tertentu, tetapi kadang-kadang mereka muncul dalam konteks yang sama sekali tidak terkait dengan geometri. Misalnya, grup dapat membentuk set numerik (misalnya, ada simetri tertentu dalam menambahkan 5 atau mengurangi 5 dari angka).

"Kelompok, pada prinsipnya, dapat muncul sebagai simetri dari hal-hal yang sama sekali berbeda," kata Zimmer.

Ada bentuk simetri yang lebih eksotis daripada yang kita pelajari di sekolah. Pertimbangkan, misalnya, simetri kisi-kisi. Kisi yang paling sederhana adalah kisi dua dimensi. Di pesawat, kisi-kisi dapat digeser ke atas, bawah, kiri, kanan oleh sejumlah kotak, dan mendapatkan kisi yang terlihat persis sama dengan aslinya. Anda juga dapat merefleksikan grid melalui sejumlah sel individual. Ruang dengan parut memiliki jumlah simetri parut yang tak terbatas.



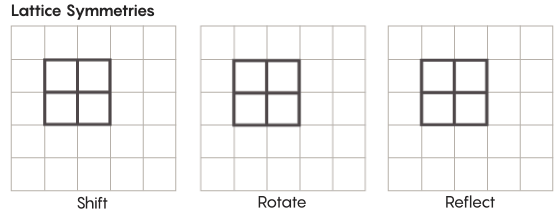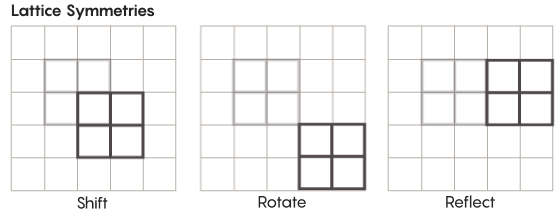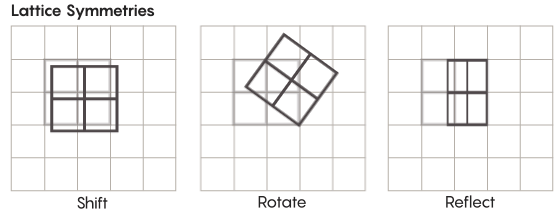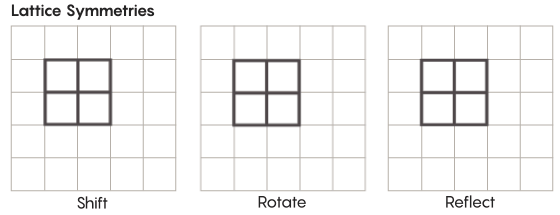
Kisi dapat ada dalam berbagai dimensi. Dalam ruang tiga dimensi, sebuah kisi dapat terdiri dari kubus, bukan kotak. Dalam empat atau lebih dimensi, tidak mungkin menyajikan kisi, tetapi ia bekerja dengan cara yang sama; matematikawan dapat menggambarkannya dengan tepat. Kelompok yang menarik bagi hipotesis Zimmer termasuk kisi "peringkat lebih tinggi", atau kisi di ruang tertentu dengan dimensi yang lebih tinggi. "Kisi aneh ini akan sangat indah, jika itu bisa dilihat, bahkan jika itu tidak diberikan kepada saya," kata Khurtado-Salazar. "Tampaknya bagiku memandangnya akan sangat menyenangkan."

Pada abad ke-20, matematikawan menemukan kelompok-kelompok ini dalam berbagai kondisi - tidak hanya dalam geometri, tetapi juga dalam teori bilangan, logika, dan ilmu komputer. Membuka kelompok baru, adalah logis untuk mengajukan pertanyaan - ruang seperti apa yang memiliki rangkaian simetri seperti itu?

Kadang-kadang kelompok jelas tidak mungkin mencocokkan ruang. Orang dapat dengan cepat memahami bahwa kelompok simetri lingkaran tidak dapat diterapkan pada kotak. Putar persegi 10 derajat dan Anda tidak akan mendapatkan persegi asli. Tetapi campuran kelompok dengan jumlah simetri dan ruang yang tak terbatas dengan banyak dimensi membuat sulit untuk menentukan penerapan kelompok.

"Ketika pindah ke grup yang lebih kompleks dalam dimensi yang lebih banyak," kata Zimmer, "masalah ini menjadi sangat rumit."

Koneksi tidak langsung

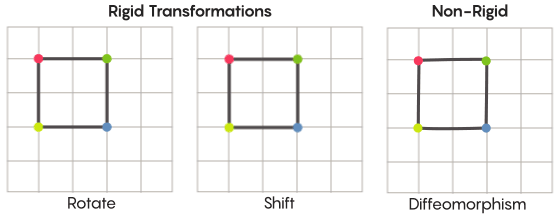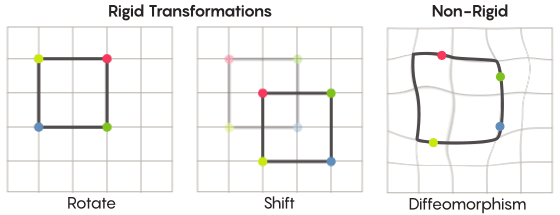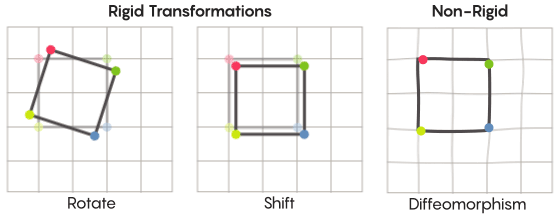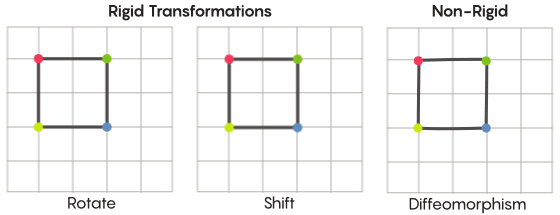
Membayangkan simetri, kita membayangkan rotasi seluruh bentuk - misalnya, persegi diputar 90 derajat. Tetapi pada tingkat dasar, simetri tergantung pada titik bergerak. Transformasi ruang simetris berarti Anda harus mengambil setiap titik dan memindahkannya ke titik lain. Dalam pengertian ini, rotasi 90 derajat persegi sebenarnya berarti Anda harus mengambil setiap titik persegi dan memutarnya 90 derajat sehingga tidak berada di tepi dari mana Anda memulai.


David fisher

Masalah poin bergerak dapat dipecahkan secara lebih kurang. Transformasi simetris yang paling akrab - refleksi dari kuadrat relatif terhadap diagonal atau rotasinya 90 derajat - sangat ketat. Ketat dalam arti bahwa mereka tidak mencampuradukkan poin. Titik-titik yang merupakan simpul sebelum refleksi tetap menjadi simpul setelah (mereka hanya menjadi simpul yang berbeda), dan titik-titik yang membentuk tepi lurus, setelah refleksi, masih membentuk tepi lurus (hanya berbeda).

Ada jenis transformasi simetris yang kurang ketat dan lebih fleksibel, dan mereka menarik dalam konteks hipotesis Zimmer. Dalam transformasi seperti itu, poin mengubah organisasi mereka lebih kuat; mereka tidak perlu mempertahankan koneksi mereka sebelumnya satu sama lain setelah transformasi. Misalnya, Anda dapat memindahkan setiap titik persegi dengan tiga unit panjang sepanjang garis bujur - ini memenuhi persyaratan dasar dari transformasi simetris, yaitu, cukup menggeser setiap titik di ruang ke tempat lain. Aaron Brown, co-penulis bukti, menggambarkan bagaimana ini transformasi bentuk lebih mungkin terlihat dalam konteks bola.

“Anda bisa mengambil kutub utara dan selatan dan memelintirnya ke arah yang berlawanan. Maka jarak antar titik akan meningkat, ”kata Brown.

Dalam kasus kisi-kisi, alih-alih hanya memindahkannya di sepanjang pesawat, Anda dapat menekuknya, merentangkannya di beberapa tempat, dan menekannya di tempat lain, sehingga mesh yang bertransformasi tidak lagi tumpang tindih dengan yang asli. Transformasi semacam itu kurang ketat, dan disebut difeomorfisme .



Zimmer punya alasan bagus untuk menggunakan versi simetri yang tidak terlalu ketat ini dalam hipotesisnya. Kisi-kisi khusus dari peringkat tertinggi yang berkaitan dengan hipotesis ini pertama kali dipelajari pada 1960-an oleh Grigory Alexandrovich Margulis , yang menerima Hadiah Fields atas karyanya. Margulis membuat deskripsi lengkap tentang ruang apa yang bisa ditransformasikan menggunakan kisi-kisi tingkat tinggi ini, jika hanya transformasi ketat yang diizinkan.

Hipotesis Zimmer menjadi kelanjutan alami dari karya Margulis. Ini dimulai dengan daftar ruang di mana kisi-kisi peringkat atas dapat bekerja - Margulis menemukan daftar ini - dan menanyakan apakah daftar ini berkembang jika kisi-kisi diizinkan memiliki transformasi yang kurang ketat.

Dalam karya baru, tiga matematikawan membuktikan bahwa melemahkan definisi simetri tidak mengubah ruang lingkup simetri kisi-kisi tingkat tinggi. Bahkan jika kisi-kisi diperbolehkan memiliki transformasi yang sangat tidak teratur - untuk bergeser, membengkokkan, meregangkan - kisi-kisi tersebut masih memiliki batasan ketat pada ruang lingkupnya.

“Setelah menambahkan fleksibilitas pada pernyataan masalah, secara intuitif, tentu saja, tampaknya grid dapat bertindak lebih luas. Oleh karena itu, ternyata mengejutkan bahwa pada kenyataannya jawabannya akan "tidak" - dalam beberapa kasus mereka tidak bisa, "kata Fisher.

Matematikawan telah membangun korespondensi yang tepat antara dimensi ruang dan dimensi, atau pangkat, dari kisi-kisi, untuk kisi-kisi yang dapat memainkan peran simetri dalam ruang yang diberikan. Secara umum, mereka menunjukkan bahwa semakin tinggi pangkat kisi, semakin banyak pengukuran yang dibutuhkan untuk ruang yang dapat menampungnya. Bahkan dengan fleksibilitas yang cukup besar dalam mentransformasikan ruang, transformasi kisi peringkat tinggi terbatas pada dimensi yang lebih tinggi.

"Ini menunjukkan bahwa ada sesuatu yang sangat mendasar dalam struktur ruang, yang menyiratkan kemampuan mereka untuk mengakomodasi transformasi seperti itu," kata Wilkinson.

Hipotesis Zimmer hanyalah langkah pertama menuju program yang lebih besar. Setelah mengatasinya, rekan penulis dari karya tersebut memberlakukan batasan kasar pada ruang di mana kisi-kisi peringkat tinggi dapat diubah. Fase selanjutnya, yang lebih ambisius dari pekerjaan ini adalah konsentrasi pada ruang-ruang tempat kisi-kisi dapat ada - dan kemudian klasifikasi semua cara berbeda untuk mengubah kisi-kisi ruang-ruang ini.

“Pada akhirnya, program harus dapat mengklasifikasikan semua metode ini. Ada banyak pertanyaan menarik di luar pendirian sederhana dari fakta keberadaan tempat-tempat tertentu di mana kisi-kisi tidak dapat beroperasi, “kata Zimmer.