🙅🏾 🕹️ 📞 Julia dan potret fase sistem dinamis 🏗️ 👇🏻 ♋️

Kami terus menguasai bahasa tujuan umum yang muda dan menjanjikan, Julia . Tetapi sebagai permulaan, kita membutuhkan kemungkinan aplikasi yang sangat sempit - untuk menyelesaikan masalah fisika yang khas. Ini adalah taktik yang paling nyaman untuk menguasai instrumen: untuk mendapatkan bantuan, kita akan memecahkan masalah yang mendesak, secara bertahap meningkatkan kompleksitas dan menemukan cara untuk membuat hidup kita lebih mudah. Singkatnya, kami akan memecahkan grafik diff dan membangun.

Untuk memulai, unduh paket grafis Gadfly , dan segera versi lengkap pengembangnya, sehingga berfungsi baik dengan Julia 1.0.1 kami. Kami mengendarai notebook REPL, JUNO atau Jupyter kami:

using Pkg pkg"add Compose#master" pkg"add Gadfly#master"

Bukan opsi yang paling nyaman, tetapi sambil menunggu pembaruan PlotlyJS , Anda dapat mencoba demi perbandingan.

Anda juga membutuhkan alat yang ampuh untuk menyelesaikan persamaan diferensial

 ]add DifferentialEquations #

Ini adalah paket paling luas dan didukung yang menyediakan banyak metode untuk menyelesaikan diffurs. Sekarang lanjutkan ke potret fase.

Solusi persamaan diferensial biasa seringkali lebih nyaman untuk digambarkan dalam bentuk yang tidak biasa $y ^ 1 (t), ..., y ^ L (t)$ , dan dalam ruang fase sepanjang sumbu di mana nilai-nilai dari masing-masing fungsi ditemukan diplot. Selain itu, argumen t termasuk dalam grafik hanya secara parametrik. Dalam kasus dua ODE, grafik seperti itu - potret fase sistem - adalah kurva pada bidang fase dan oleh karena itu sangat jelas.

Osilator

Dinamika Osilator Harmonik $\ gamma$ dijelaskan oleh sistem persamaan berikut:

d o t x = y d o t y = - o m e g a^{2} x + g a m m a y

$\ dot {x} = y \\ \ dot {y} = - \ omega ^ 2x + \ gamma y$

dan terlepas dari kondisi awal (x0, y0), ia datang ke keadaan keseimbangan, titik (0,0) dengan sudut defleksi nol dan kecepatan nol.

Di $\ gamma = 0$ solusi mengambil karakteristik bentuk osilator klasik.

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end

Mari kita menganalisis kodenya. Fungsi menerima nilai frekuensi dan parameter pelemahan, serta kondisi awal. Fungsi nested syst () mendefinisikan sistem. Agar itu berubah, mereka menggunakan perkalian matriks satu baris. Fungsi resol () , mengambil sejumlah besar parameter, sangat fleksibel dikonfigurasi untuk menyelesaikan masalah, tetapi kami hanya menunjukkan metode solusi - Runge-Kutta 4 ( ada banyak lainnya ), kesalahan relatif, dan fakta bahwa tidak semua titik harus disimpan, tetapi hanya setiap keempat . Matriks respons disimpan dalam variabel sol , apalagi, sol.t berisi vektor waktu, dan sol.u memecahkan sistem pada waktu-waktu ini. Semua ini dengan tenang digambarkan dalam Plot , dan untuk Gadfly Anda harus menyelesaikan jawaban dalam matriks yang lebih nyaman. Kami tidak perlu waktu, jadi kami hanya mengembalikan solusi.

Mari kita membangun potret fase:

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2])

Di antara fungsi-fungsi tingkat tinggi, broadcast(f, [1, 2, 3]) sangat penting bagi kami, yang secara bergantian mengganti nilai-nilai array [1, 2, 3] ke dalam fungsi f . Rekor pendek f.([1, 2, 3]) . Ini berguna untuk memvariasikan frekuensi, parameter atenuasi, koordinat awal dan kecepatan awal.

Tersembunyi di bawah spoiler

 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #

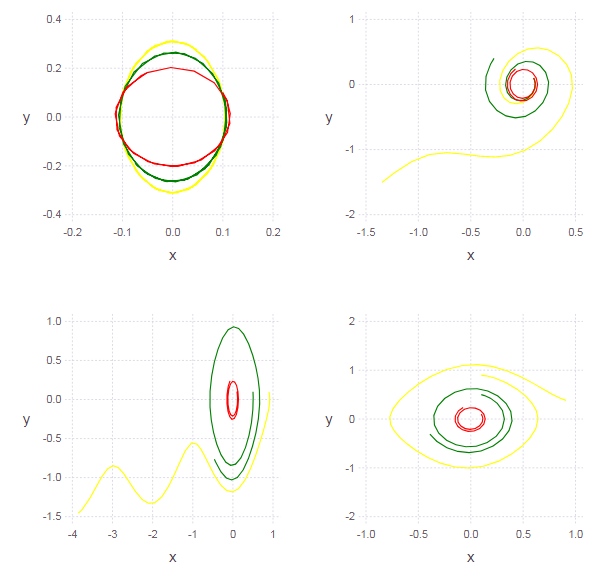
Sekarang kami menganggap bukan osilasi kecil, tetapi osilasi amplitudo sewenang-wenang:

d o t x = y d o t y = - s i n (o m e g a x) + g a m m a y

$\ dot {x} = y \\ \ dot {y} = - sin (\ omega x) + \ gamma y$

Diagram fase dari solusi bukanlah elips (yang menunjukkan nonlinier dari osilator). Semakin sedikit kita memilih amplitudo osilasi (yaitu, kondisi awal), semakin sedikit nonlinier akan muncul (oleh karena itu, osilasi kecil dari pendulum dapat dianggap harmonis).

Tersembunyi di bawah spoiler

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) )

Brusselator

Model ini menggambarkan reaksi kimia autokatalitik tertentu di mana difusi berperan. Model ini diusulkan pada tahun 1968 oleh Lefebvre dan Prigozhin.

d o t u_{1} = - (m u + 1) u_{1} + u_{1}^{2} u_{2} + 1 d o t u_{2} = m u u_{1} - u_{1}^{2} u_{2}

$\ dot {u} _1 = - (\ mu + 1) u_1 + u ^ 2_1u_2 + 1 \\ \ dot {u} _2 = \ mu u_1-u ^ 2_1u_2$

Fungsi tidak dikenal $u_1 (t), \, u_2 (t)$ mencerminkan dinamika konsentrasi produk antara dari suatu reaksi kimia. Parameter model $\ mu$ konsentrasi awal katalis (zat ketiga) masuk akal.

Secara lebih rinci, evolusi potret fase brusselator dapat diamati dengan melakukan perhitungan dengan berbagai parameter $\ mu$ . Dengan kenaikannya, node pertama-tama akan secara bertahap bergeser ke titik dengan koordinat (1, $\ mu$ ) hingga mencapai nilai bifurkasi $\ mu$ = 2. Pada titik ini, ada restrukturisasi kualitatif potret, yang dinyatakan dalam kelahiran siklus batas. Dengan peningkatan lebih lanjut $\ mu$ hanya perubahan kuantitatif dalam parameter siklus ini terjadi.

Tersembunyi di bawah spoiler

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) )

Cukup untuk hari ini. Lain kali, kami akan mencoba mempelajari cara menggunakan paket grafik lain untuk tugas-tugas baru, sementara secara bersamaan mengetik tangan kami di sintaks Julia. Dalam proses penyelesaian masalah, perlahan-lahan mulai ditelusuri, bukan karena pro dan kontra itu langsung ... melainkan, fasilitas dan ketidaknyamanan - percakapan terpisah harus dikhususkan untuk ini. Dan, tentu saja, saya ingin melihat sesuatu yang lebih serius pada habra saya daripada permainan saya dengan fungsi - karena itu, saya mendesak para ahli hukum untuk menceritakan lebih banyak tentang proyek yang lebih serius, ini akan membantu banyak orang, dan khususnya, dalam mempelajari bahasa yang indah ini.

Julia dan potret fase sistem dinamis

Osilator

Brusselator

More articles: