👨🏽‍⚕️ 🌺 ♻️ Julia dan persamaan diferensial parsial 🕴🏻 🙇🏼 🤵

Pada contoh model fisik paling khas, kami akan menggabungkan keterampilan bekerja dengan fungsi dan berkenalan dengan visualizer PyPlot yang cepat, nyaman dan indah, yang menyediakan semua kekuatan Python Matplotlib. Akan ada banyak gambar (tersembunyi di bawah spoiler)

Kami memastikan bahwa semuanya bersih dan segar di bawah tenda:

Di bawah tenda

]status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.13.0+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Kalau tidak, kita akan mendapatkan semua yang kita butuhkan untuk hari ini

 julia>] pkg> add PyCall pkg> add LaTeXStrings pkg> add PyPlot pkg> build PyPlot #     build #    -      ,    pkg> add Conda #    Jupyter -    pkg> add IJulia #      pkg> build IJulia #     build

Sekarang untuk tugas!

Bawa persamaan

Dalam fisika, istilah transfer dipahami sebagai proses yang tidak dapat diubah, sebagai akibatnya perpindahan spasial (transfer) massa, momentum, energi, muatan, atau sejumlah fisik lainnya terjadi dalam sistem fisik.
Persamaan transportasi satu dimensi linier (atau persamaan adveksi) - persamaan diferensial parsial paling sederhana - ditulis sebagai

f r a c p a r t i a l U (x, t) p a r t i a l t + c f r a c p a r t i a l U (x, t) p a r t i a l x = P h i (U, x, t)

$\ frac {\ partial U (x, t)} {\ partial t} + c \ frac {\ partial U (x, t)} {\ partial x} = \ Phi (U, x, t)$

Untuk solusi numerik dari persamaan transport, Anda dapat menggunakan skema perbedaan eksplisit:

f r a c h a t U_{i} - U_{i} t a u + c f r a c U_{i} - U_{i - 1} D e l t a = f r a c P h i_{i - 1} + P h i_{i} 2

$\ frac {\ hat {U} _i-U_i} {\ tau} + c \ frac {U_i-U_ {i-1}} {\ Delta} = \ frac {\ Phi_ {i-1} + \ Phi_i} {2}$

dimana $\ hat {U}$ - nilai fungsi grid pada lapisan waktu atas. Sirkuit ini stabil dengan nomor Courant. $K = c \ tau / \ Delta <1$

Transfer nonlinier

f r a c p a r t i a l U (x, t) p a r t i a l t + (C_{0} + U C_{1}) f r a c p a r t i a l U (x, t) p a r t i a l x = P h i (U, x, t)

$\ frac {\ partial U (x, t)} {\ partial t} + (C_0 + UC_1) \ frac {\ partial U (x, t)} {\ partial x} = \ Phi (U, x, t )$

Sumber garis (transfer penyerapan): $\ Phi (U, x, t) = - BU$ . Kami menggunakan skema perbedaan eksplisit:

U_{i}^{j + 1} = k i r i (1 - f r a c h_{t} B 2 - f r a c h_{t} C_{0} h_{x} - f r a c h_{t} C_{1} h_{x} U_{i}^{j} k a n a n) U_{i}^{j} + U_{i - 1}^{j} k i r i (f r a c h_{t} C_{0} h_{x} - f r a c h_{t} B 2 + f r a c h_{t} C_{1} h_{x} U_{i}^{j} k a n a n)

$U ^ {j + 1} _i = \ kiri (1- \ frac {h_tB} {2} - \ frac {h_tC_0} {h_x} - \ frac {h_tC_1} {h_x} U ^ j_i \ kanan) U ^ j_i + U ^ j_ {i-1} \ kiri (\ frac {h_tC_0} {h_x} - \ frac {h_tB} {2} + \ frac {h_tC_1} {h_x} U ^ j_i \ kanan)$

 using Plots pyplot() a = 0.2 b = 0.01 ust = x -> x^2 * exp( -(xa)^2/b ) #   bord = t -> 0. #  #    - function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt b0 = 0.5B*dt c0 = C0*dt/dx c1 = C1*dt/dx print("Kurant: $c0 $c1") x = [i for i in range(0, length = Nx, step = dx)]#         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[:,1] = ust.(x) U[1,:] = bord.(t) for j = 1:Nt-1, i = 2:Nx U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j] end t, x, U end t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 ) plot(X, Ans0[:,1], lab = "t1") plot!(X, Ans0[:,10], lab = "t10") p = plot!(X, Ans0[:,40], lab = "t40") plot( p, heatmap(t, X, Ans0) ) #

Hasil

Mari tingkatkan penyerapan:

 t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,10]) p = plot!(X, Ans0[:,40]) plot( p, heatmap(t, X, Ans0) )

Hasil

 t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100, tlmt = 0.4 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,20]) plot!(X, Ans0[:,90])

Hampir jatuh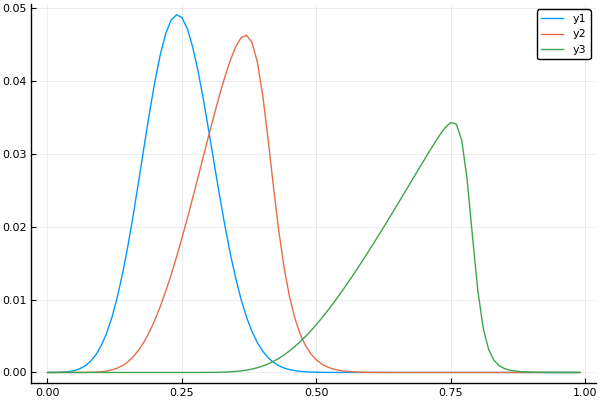

heatmap(t, X, Ans0)

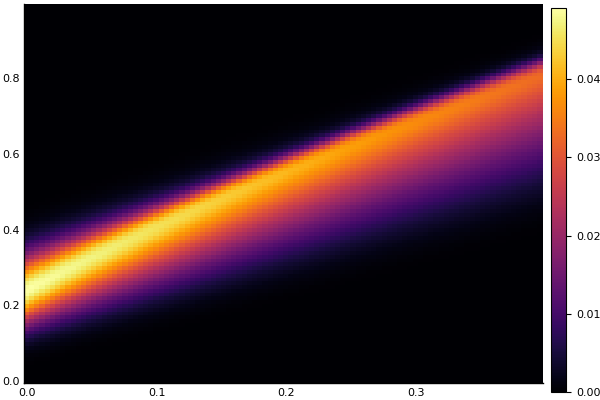
Persamaan panas

Persamaan panas diferensial (atau persamaan difusi panas) ditulis sebagai berikut:

f r a c p a r t i a l T (x, t) p a r t i a l t + D f r a c p a r t i a l^{2} U (x, t) p a r t i a l x^{2} = p h i (T, x, t)

$\ frac {\ partial T (x, t)} {\ partial t} + D \ frac {\ partial ^ 2 U (x, t)} {\ partial x ^ 2} = \ phi (T, x, t )$

Ini adalah persamaan parabola yang mengandung turunan pertama sehubungan dengan waktu t dan yang kedua sehubungan dengan koordinat spasial x. Ini menggambarkan dinamika suhu, misalnya, batang logam pendingin atau pemanas (fungsi T menggambarkan profil suhu sepanjang koordinat x sepanjang batang). Koefisien D disebut koefisien konduktivitas termal (difusi). Ini bisa berupa konstan atau tergantung, baik secara eksplisit pada koordinat, dan pada fungsi yang diinginkan D (t, x, T) itu sendiri.

Pertimbangkan persamaan linier (koefisien difusi dan sumber panas tidak tergantung suhu). Perbedaan perkiraan persamaan diferensial menggunakan skema Euler eksplisit dan implisit, masing-masing:

f r a c T_{i, n + 1} - T_{i, n} t a u = D f r a c T_{i - 1, n} - 2 T_{i, n} + T_{i + 1, n} D e l t a^{2} + p h i_{i, n} f r a c T_{i, n + 1} - T_{i, n} t a u = D f r a c T_{i - 1, n + 1} - 2 T_{i, n + 1} + T_{i + 1, n + 1} D e l t a^{2} + p h i_{i, n}

$\ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ {i-1, n} -2T_ {i, n} + T_ {i + 1 , n}} {\ Delta ^ 2} + \ phi_ {i, n} \\ \ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ { i-1, n + 1} -2T_ {i, n + 1} + T_ {i + 1, n + 1}} {\ Delta ^ 2} + \ phi_ {i, n}$

 δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # -     startcond = x-> δ(x-0.45) - δ(x-0.55) #   bordrcond = x-> 0. #    D(u) = 1 #   Φ(u) = 0 #    #      LaTex    Tab # \delta press Tab -> δ function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)") x = [i for i in range(0, length = Nx, step = dx)] #         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[: ,1] = startcond.(x) U[1 ,:] = U[Nt,:] = bordrcond.(t) for j = 1:Nt-1, i = 2:Nx-1 U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j]) end t, x, U end t, X, Ans2 = linexplicit( tlmt = 0.005 ) plot(X, Ans2[:,1], lab = "t1") plot!(X, Ans2[:,10], lab = "t10") p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme") plot( p, heatmap(t, X, Ans2) )

Hasil

Kami menggunakan skema implisit dan metode sapuan

 function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n") x = [i for i in range(0, length = Nx, step = dx)] t = [i for i in range(0, length = Nt, step = dt)] U = zeros(Nx, Nt) η = zeros(Nx+1) ξ = zeros(Nx) U[: ,1] = startcond.(x) U[1 ,:] = bordrcond.(t) U[Nt,:] = bordrcond.(t) for j = 1:Nt-1 b = -1 - 2k*D( U[1,j] ) c = -k*D( U[2,j] ) d = U[1,j] + dt*Φ(U[1,j]) ξ[2] = c/b η[2] = -d/b for i = 2:Nx-1 a = -k*D( U[i-1,j] ) b = -2k*D( U[i,j] ) - 1 c = -k*D( U[i+1,j] ) d = U[i,j] + dt*Φ(U[i,j]) ξ[i+1] = c / (ba*ξ[i]) η[i+1] = (a*η[i]-d) / (ba*ξ[i]) end U[Nx,j+1] = η[Nx] for i = Nx:-1:2 U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i] end end t, x, U end plot(X, Ans2[:,1], lab = "ex_t1") plot!(X, Ans2[:,10], lab = "ex_t10") plot!(X, Ans2[:,40], lab = "ex_t40") plot!(X, Ans3[:,1], lab = "non_t1") plot!(X, Ans3[:,10], lab = "non_t10") plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")

Perbandingan sirkuit

Persamaan panas nonlinier

Solusi yang jauh lebih menarik dapat diperoleh untuk persamaan panas nonlinier, misalnya, dengan sumber panas nonlinier $\ phi (x, T) = 10 ^ 3 (T-T ^ 3)$ . Jika Anda mengaturnya dalam bentuk ini, Anda mendapatkan solusi dalam bentuk front termal, merambat di kedua sisi zona pemanasan primer

 Φ(u) = 1e3*(uu^3) t, X, Ans4 = linexplicit( tlmt = 0.005 ) plot(X, Ans4[:,1], lab = "ex_t1") plot!(X, Ans4[:,10], lab = "ex_t10") plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")

Depan termal

Solusi yang lebih tak terduga juga dimungkinkan dengan nonlinier dari koefisien difusi juga. Misalnya, jika Anda mengambil $D (x, T) = T ^ 2$ , a $\ phi (x, T) = 10 ^ 3T ^ {3,5}$ , maka seseorang dapat mengamati efek pembakaran medium, terlokalisasi di wilayah pemanasan utamanya (S-mode pembakaran “dengan eksaserbasi”).
Pada saat yang sama, kami akan memeriksa bagaimana skema implisit kami bekerja dengan nonlinier dari kedua sumber dan koefisien difusi

 D(u) = u*u Φ(u) = 1e3*abs(u)^(3.5) t, X, Ans5 = linexplicit( tlmt = 0.0005 ) t, X, Ans6 = nonexplicit( tlmt = 0.0005 ) plot(X, Ans5[:,1], lab = "ex_t1") plot!(X, Ans5[:,10], lab = "ex_t10") p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation") p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") #      plot(p1, p2)

Mode S

Persamaan gelombang

Persamaan Gelombang Hiperbolik

f r a c p a r t i a l^{2} U (x, t) p a r t i a l t^{2} = c^{2} f r a c p a r t i a l^{2} U (x, t) p a r t i a l x^{2}

$\ frac {\ partial ^ 2 U (x, t)} {\ partial t ^ 2} = c ^ 2 \ frac {\ partial ^ 2 U (x, t)} {\ partial x ^ 2}$

menggambarkan gelombang linear satu dimensi tanpa dispersi. Misalnya, getaran string, suara dalam cairan (gas) atau gelombang elektromagnetik dalam ruang hampa (dalam kasus terakhir, persamaan harus ditulis dalam bentuk vektor).

Skema perbedaan paling sederhana yang mendekati persamaan ini adalah skema lima poin eksplisit

f r a c U_{i}^{n + 1} - 2 U_{i}^{n} + U_{i}^{n - 1} t a u^{2} = c^{2} f r a c U_{i + 1}^{n} - 2 U_{i}^{n} + U_{i - 1}^{n} h^{2} x_{i} = i h, t_{n} = t a u

$\ frac {U ^ {n + 1} _i-2U ^ {n} _i + U ^ {n-1} _i} {\ tau ^ 2} = c ^ 2 \ frac {U ^ n_ {i + 1} -2U ^ n_i + U ^ n_ {i-1}} {h ^ 2} \\ x_i = ih, \, t_n = \ tau$

Skema ini, yang disebut "salib", memiliki urutan keakuratan kedua dalam waktu dan koordinat spasial dan tiga lapis waktu.

 #     ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 ) #    ϕ(x) = 0 c = x -> 1 #     function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 ) dx = L/N; dt = T/K; gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx; print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt") u = zeros(N,K); x = [i for i in range(0, length = N, step = dx)] #      u[:,1] = ψ.(x); u[:,2] = u[:,1] + dt*ψ.(x); #     fill!( u[1,:], 0); fill!( u[N,:], ϕ(L) ); for t = 2:K-1, i = 2:N-1 u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t]; end x, u end N = 50; #     K = 40; #    a = 0.1; #    L = 1; #   T = 1; #   t = [i for i in range(0, length = K, stop = T)] X, U = pdesolver(N, K, L, T, a) #    plot(X, U[:,1]) plot!(X, U[:,40])

Hasil

Untuk membangun permukaan, kami akan menggunakan PyPlot sebagai lingkungan Plots, tetapi secara langsung:

Grafik permukaan

 using PyPlot surf(t, X, U)

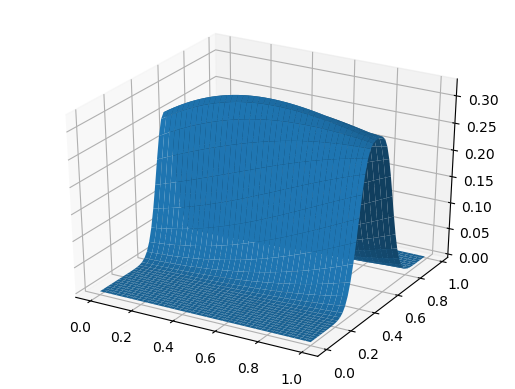
Dan untuk hidangan penutup, gelombang menyebar dengan cepat tergantung pada koordinat:

 ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2 c = x -> x>0.5 ? 0.5 : 1 X, U = pdesolver(400, 400, 8, 1.5, 1) plot(X, U[:,1]) plot!(X, U[:,40]) plot!(X, U[:,90]) plot!(X, U[:,200], xaxis=("  ", (0, 1.5), 0:0.5:2) )

Hasil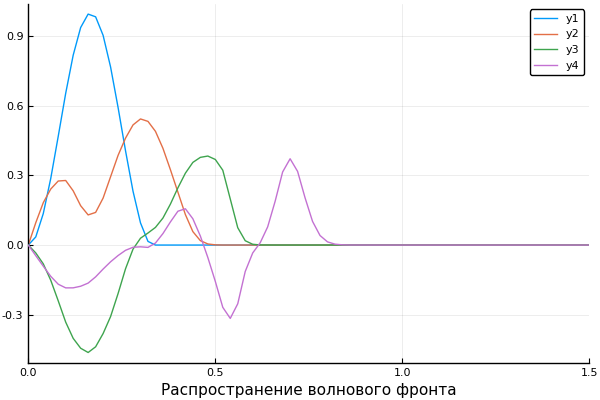

 U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ] #    surf(U2) #

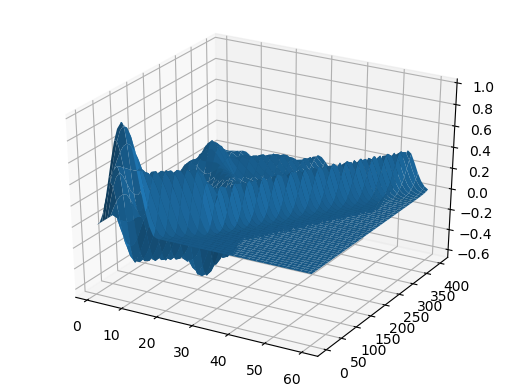
heatmap(U, yaxis=(" ", (0, 50), 0:10:50))

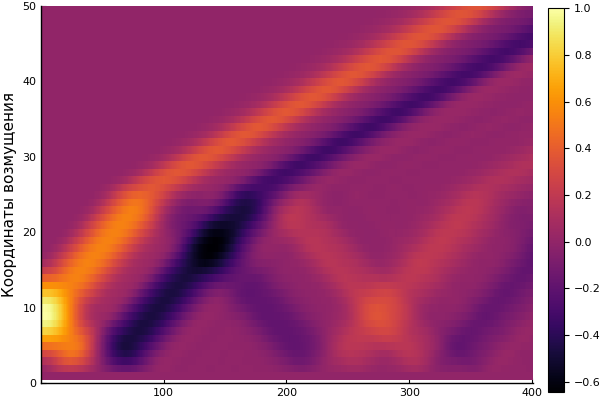
Cukup untuk hari ini. Untuk ulasan lebih rinci:
Tautan PyPlot ke github , contoh Plot lain yang digunakan sebagai lingkungan, dan memo berbahasa Rusia yang bagus oleh Julia .

Julia dan persamaan diferensial parsial

Bawa persamaan

Transfer nonlinier

Persamaan panas

Persamaan panas nonlinier

Persamaan gelombang

More articles: