Sebuah auto-encoder variasional (auto-encoder) adalah model generatif yang belajar untuk menampilkan objek dalam ruang tersembunyi yang diberikan.

Pernah bertanya-tanya bagaimana model variational auto-encoder (VAE) bekerja? Ingin tahu bagaimana VAE menghasilkan contoh-contoh baru seperti set data yang dilatihnya? Setelah membaca artikel ini, Anda akan mendapatkan pemahaman teoritis tentang cara kerja internal VAE, dan Anda juga dapat menerapkannya sendiri. Lalu saya akan menunjukkan kode VAE yang bekerja dilatih pada set digit tulisan tangan, dan kami akan bersenang-senang, menghasilkan digit baru!

Model Generatif

VAE adalah model generatif - ini memperkirakan kepadatan probabilitas (PDF) dari data pelatihan. Jika model seperti itu dilatih dalam gambar alami, maka itu akan menetapkan nilai probabilitas tinggi untuk gambar singa, dan nilai rendah untuk gambar omong kosong acak.

Model VAE juga tahu cara mengambil contoh dari PDF yang terlatih, yang merupakan bagian paling keren, karena dapat menghasilkan contoh baru yang mirip dengan dataset asli!

Saya akan menjelaskan VAE menggunakan set nomor tulisan tangan MNIST . Data input untuk model adalah gambar dalam format $$$\ mathbb {R} ^ {28 × 28}$. Model harus menilai kemungkinan seberapa banyak input tampak seperti digit.

Tugas pemodelan gambar

Interaksi antara piksel adalah tugas yang sulit. Jika piksel tidak saling bergantung satu sama lain, maka Anda perlu mempelajari PDF dari setiap piksel secara independen, yang mudah. Pilihannya juga sederhana - kami mengambil setiap piksel secara terpisah.

Namun dalam gambar digital, ada ketergantungan yang jelas antara piksel. Jika Anda melihat awal dari empat di setengah kiri, Anda akan sangat terkejut jika setengah kanan adalah penyelesaian nol. Tapi kenapa?

Ruang tersembunyi

Anda tahu bahwa setiap gambar memiliki satu nomor. Pintu masuk ke $$$\ mathbb {R} ^ {28 × 28}$jelas tidak mengandung informasi ini. Tapi itu pasti di suatu tempat ... "suatu tempat" ini adalah ruang tersembunyi.



Anda dapat menganggap ruang tersembunyi sebagai $$$\ mathbb {R} ^ {k}$di mana setiap vektor berisi $$$k$potongan informasi yang diperlukan untuk membuat gambar. Misalkan dimensi pertama berisi angka yang diwakili oleh digit. Dimensi kedua mungkin lebar. Yang ketiga adalah sudut, dan sebagainya.

Kita bisa membayangkan proses menggambar seseorang dalam dua langkah. Pertama, seseorang menentukan - secara sadar atau tidak - semua atribut nomor yang akan ditampilkan. Selanjutnya, keputusan-keputusan ini ditransformasikan menjadi stroke di atas kertas.

VAE mencoba mensimulasikan proses ini: untuk gambar yang diberikan $$$x$kami ingin menemukan setidaknya satu vektor tersembunyi yang dapat menggambarkannya; satu vektor berisi instruksi untuk menghasilkan $$$x$. Merumuskannya dengan rumus probabilitas total , kita dapatkan $$$P (x) = \ int P (x | z) P (z) dz$.

Mari kita masuk akal ke dalam persamaan ini:

• Integral berarti bahwa kandidat harus dicari di semua ruang tersembunyi.
• Untuk setiap kandidat $$$z$kami mengajukan pertanyaan: apakah mungkin untuk menghasilkan $$$x$menggunakan instruksi $$$z$? Cukup besar $$$P (x | z)$? Misalnya, jika $$$z$mengkodekan informasi tentang angka 7, maka gambar 8 tidak mungkin. Namun, gambar 1 dapat diterima karena 1 dan 7 serupa.
• Kami menemukan yang bagus. $$$z$? Hebat! Tapi tunggu sebentar ... berapa harganya $$$z$mungkin? $$$P (z)$cukup besar? Pertimbangkan gambar dari angka terbalik 7. Pencocokan ideal adalah vektor tersembunyi yang menggambarkan tampilan 7, di mana ukuran sudut diatur ke 180 °. Namun demikian $$$z$Ini tidak mungkin, karena biasanya angka tidak ditulis pada sudut 180 °.

Tujuan pelatihan VAE adalah untuk memaksimalkan $$$P (x)$. Kami akan membuat model $$$P (x | z)$menggunakan distribusi Gaussian multidimensi $$$\ mathcal {N} (f (z), \ sigma ^ 2 \ cdot I)$.

$$$f (z)$dimodelkan menggunakan jaringan saraf. $$$\ sigma$Merupakan hiperparameter untuk mengalikan matriks identitas $$$I$.

Ingat itu $$$f$- inilah yang akan kami gunakan untuk menghasilkan gambar baru menggunakan model yang terlatih. Tumpang tindih distribusi Gaussian hanya untuk tujuan pendidikan. Jika kita menggunakan fungsi Dirac delta (mis., Deterministik $$$x = f (z)$), maka kita tidak akan bisa melatih model menggunakan gradient descent!

Keajaiban ruang tersembunyi

Pendekatan ruang tersembunyi memiliki dua masalah besar:

1. Informasi apa yang dimiliki setiap dimensi? Beberapa dimensi mungkin berhubungan dengan elemen abstrak, seperti gaya. Meskipun mudah untuk menginterpretasikan semua dimensi, kami tidak ingin menetapkan label ke kumpulan data. Pendekatan ini tidak skala ke set data lainnya.
2. Ruang tersembunyi bisa membingungkan ketika ada korelasi antara dimensi. Misalnya, nomor yang ditarik sangat cepat secara bersamaan dapat menyebabkan munculnya stroke sudut dan lebih tipis. Mendefinisikan dependensi ini sulit.

Pembelajaran mendalam datang untuk menyelamatkan

Ternyata setiap distribusi dapat dihasilkan dengan menerapkan fungsi yang agak rumit untuk distribusi Gaussian multidimensi standar.

Pilih $$$P (z)$sebagai distribusi Gaussian multidimensi standar. Demikian dimodelkan oleh jaringan saraf $$$f$dapat dibagi menjadi dua fase:

1. Lapisan pertama memetakan distribusi Gaussian ke dalam distribusi sebenarnya di ruang tersembunyi. Kami tidak dapat menafsirkan pengukuran, tetapi itu tidak masalah.
2. Lapisan selanjutnya akan ditampilkan dari ruang tersembunyi di $$$P (x | z)$.

Jadi bagaimana kita melatih makhluk buas ini?

Formula untuk $$$P (x)$tidak larut, oleh karena itu, kami memperkirakannya dengan metode Monte Carlo:

1. Seleksi $$$\ {z_i \} _ {i = 1} ^ n$ dari sebelumnya $$$P (z)$
2. Perkiraan dengan $$$P (x) \ approx \ frac {1} {n} \ sum_ {i = 1} ^ n P (x | z_i)$

Hebat! Jadi coba saja banyak yang berbeda $$$z$dan mulai pesta propagasi bug!

Sayangnya sejak itu $$$x$sangat multidimensi, untuk mendapatkan perkiraan yang masuk akal, banyak sampel diperlukan. Maksud saya jika Anda mencoba $$$z$, lalu bagaimana peluang mendapatkan gambar yang terlihat seperti $$$x$? Omong-omong, ini menjelaskan mengapa $$$P (x | z)$harus menetapkan nilai probabilitas positif untuk gambar yang mungkin, jika tidak model tidak akan dapat belajar: pengambilan sampel $$$z$akan menghasilkan gambar yang hampir pasti berbeda dari $$$x$, dan jika probabilitasnya adalah 0, maka gradien tidak akan dapat diperbanyak.

Bagaimana cara mengatasi masalah ini?

Potong jalan!

Sebagian besar sampel $$$z$tidak ada yang akan ditambahkan dari seleksi ke $$$P (x)$- Mereka terlalu jauh melampaui perbatasannya. Sekarang, jika Anda tahu sebelumnya ke mana harus mengambilnya dari ...

Bisa masuk $$$Q (z | x)$. Diberikan $$$Q$akan dilatih untuk menetapkan nilai probabilitas tinggi $$$z$yang cenderung menghasilkan $$$x$. Sekarang Anda dapat membuat penilaian menggunakan metode Monte Carlo, dengan mengambil sampel jauh lebih sedikit $$$Q$.

Sayangnya, masalah baru muncul! Alih-alih memaksimalkan $$$P (x) = \ int P (x | z) P (z) dz = \ mathbb {E} _ {z \ sim P (z)} P (x | z)$kami memaksimalkan $$$\ mathbb {E} _ {z \ sim Q (z | x)} P (x | z)$. Bagaimana mereka terkait satu sama lain?

Kesimpulan variasi

Kesimpulan variasional adalah topik dari artikel yang terpisah, jadi saya tidak akan membahasnya di sini secara rinci. Saya hanya bisa mengatakan bahwa distribusi ini terkait dengan persamaan ini:

$$

$$log P (X) - \ mathcal {KL} [Q (z | x) || P (z | x)] = \ mathbb {E} _ {z \ sim Q (z | x)} [log P (x | z)] - \ mathcal {KL} [Q (z | x) || P (z)]$$

$$$\ mathcal {KL}$adalah jarak Kullback - Leibler , yang secara intuitif menilai kesamaan dari dua distribusi.

Sebentar lagi, Anda akan melihat cara memaksimalkan sisi kanan persamaan. Dalam hal ini, sisi kiri juga dimaksimalkan:

• $$$P (x)$dimaksimalkan.
• seberapa jauh $$$Q (z | x)$dari $$$P (z | x)$- Nyata a priori tidak diketahui - akan diminimalkan.

Arti dari sisi kanan persamaan adalah bahwa kita memiliki ketegangan di sini:

1. Di satu sisi, kami ingin memaksimalkan seberapa baik $$$x$harus diterjemahkan dari $$$z \ sim Q$.
2. Di sisi lain, kami ingin $$$Q (z | x)$( encoder ) mirip dengan yang sebelumnya $$$P (z)$(Distribusi Gaussian multidimensi). Ini dapat dilihat sebagai regularisasi.

Meminimalkan perbedaan $$$\ mathcal {KL}$dilakukan dengan mudah dengan pemilihan distribusi yang tepat. Kami akan mensimulasikan $$$Q (z | x)$sebagai jaringan saraf, output yang merupakan parameter dari distribusi Gaussian multidimensi:

• rata-rata $$$\ mu_Q$
• matriks kovarians diagonal $$$\ Sigma_Q$

Lalu divergensi $$$\ mathcal {KL}$menjadi analitis, yang bagus untuk kita (dan untuk gradien).

Bagian decoder sedikit lebih rumit. Pada pandangan pertama, saya ingin menyatakan bahwa masalah ini tidak dapat diselesaikan dengan metode Monte Carlo. Tapi sampelnya $$$z$dari $$$Q$tidak akan mengizinkan gradien untuk disebarkan $$$Q$, karena pemilihannya bukan operasi yang dapat dibedakan. Ini adalah masalah, sejak itu bobot lapisan mengeluarkan $$$\ Sigma_Q$dan $$$\ mu_Q$.

Trik parameterisasi baru

Kita bisa ganti $$$Q$transformasi parametrized deterministik dari variabel acak nonparametrik:

1. Sampel dari distribusi Gaussian standar (tanpa parameter).
2. Mengalikan Sampel dengan Root Square $$$\ Sigma_Q$.
3. Menambah hasilnya $$$\ mu_Q$.

Akibatnya, kami memperoleh distribusi yang sama dengan $$$Q$. Sekarang operasi pengambilan berasal dari distribusi Gaussian standar. Akibatnya, gradien dapat merambat melalui $$$\ Sigma_Q$dan $$$\ mu_Q$karena sekarang ini adalah jalur deterministik.

Hasil? Model akan dapat mempelajari cara menyesuaikan parameter $$$Q$: dia akan berkonsentrasi pada yang baik $$$z$yang mampu menghasilkan $$$x$.

Menyatukan semuanya

Model VAE mungkin sulit dipahami. Kami telah memeriksa di sini banyak bahan yang sulit dicerna.

Izinkan saya merangkum semua langkah untuk mengimplementasikan VAE.



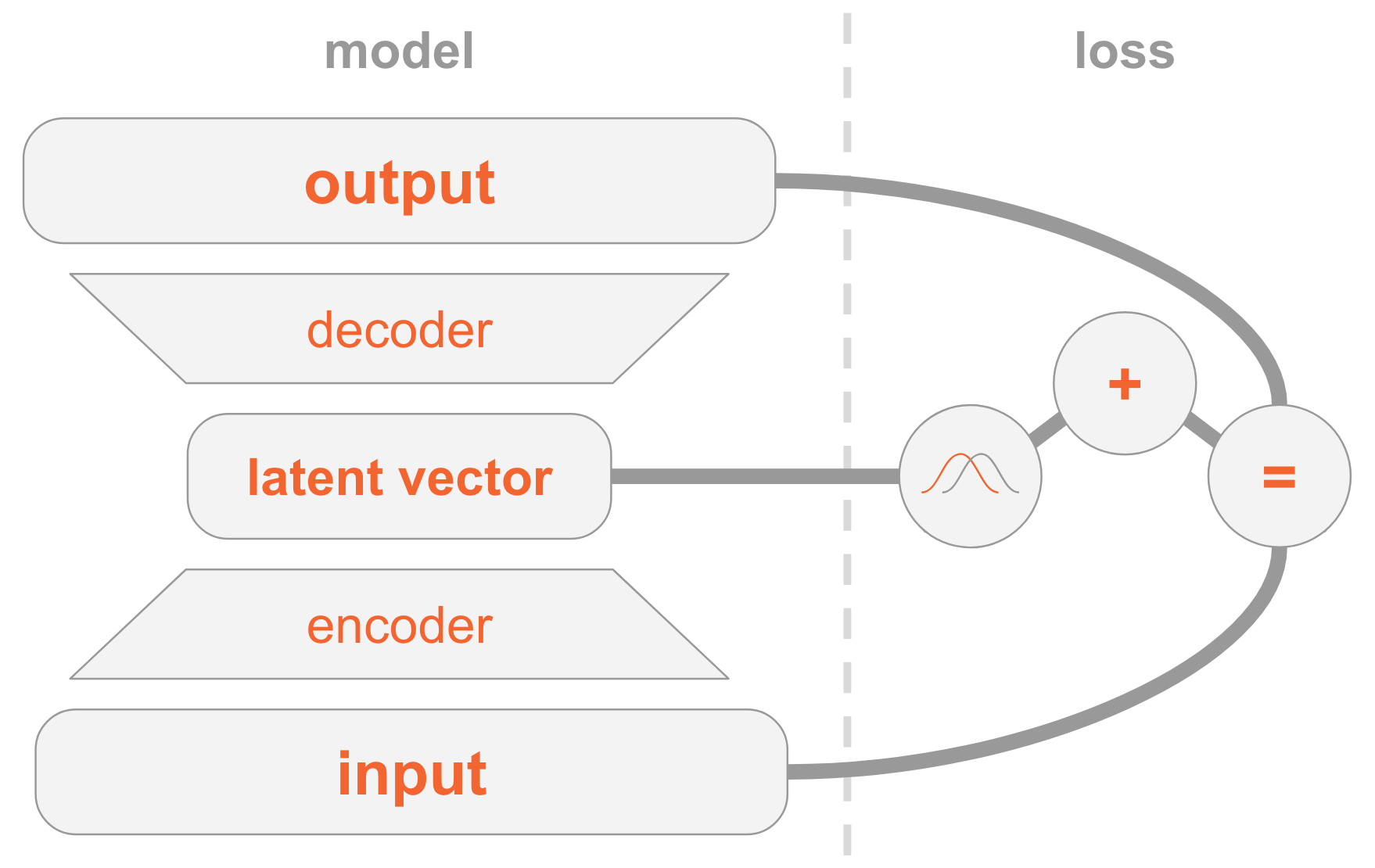
Di sebelah kiri kami memiliki definisi model:

1. Gambar input ditransmisikan melalui jaringan encoder.
2. Encoder menyediakan parameter distribusi $$$Q (z | x)$.
3. Vektor tersembunyi $$$z$diambil dari $$$Q (z | x)$. Jika encoder terlatih dengan baik, maka dalam banyak kasus $$$z$berisi deskripsi $$$x$.
4. Decoder decode $$$z$ke dalam gambar.

Di sisi kanan, kami memiliki fungsi kerugian:

1. Kesalahan pemulihan: output harus sama dengan input.
2. $$$Q (z | x)$harus mirip dengan yang sebelumnya, yaitu, distribusi normal standar multidimensi.

Untuk membuat gambar baru, Anda dapat langsung memilih vektor tersembunyi dari distribusi sebelumnya dan mendekodekannya menjadi gambar.

Kode kerja

Sekarang kita akan mempelajari VAE lebih terinci dan mempertimbangkan kode kerja. Anda akan memahami semua detail teknis yang diperlukan untuk mengimplementasikan VAE. Sebagai bonus, saya akan menunjukkan trik yang menarik: cara menetapkan peran khusus ke beberapa dimensi vektor tersembunyi sehingga model mulai menghasilkan gambar angka yang ditunjukkan.

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline 

Saya mengingatkan Anda bahwa model dilatih tentang MNIST - satu set angka tulisan tangan. Input gambar datang dalam format $$$\ mathbb {R} ^ {28 × 28}$.

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10 

Selanjutnya, kita mendefinisikan hyperparameters.

Jangan ragu untuk bermain dengan nilai-nilai yang berbeda untuk mendapatkan gambaran tentang bagaimana mereka memengaruhi model.

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 } 

Model

Model ini terdiri dari tiga subnet:

1. Mendapat $$$x$(gambar), mengkodekannya menjadi distribusi $$$Q (z | x)$di ruang tersembunyi.
2. Mendapat $$$z$di ruang tersembunyi (representasi kode dari gambar), menerjemahkannya ke dalam gambar yang sesuai $$$f (z)$.
3. Mendapat $$$x$dan menentukan angka dengan perbandingan dengan lapisan 10-dimensi, di mana nilai ke-i mengandung probabilitas angka ke-ke-10.

Dua subnet pertama adalah dasar dari VAE murni.

Yang ketiga adalah tugas bantu yang menggunakan beberapa dimensi tersembunyi untuk menyandikan angka yang ditemukan dalam gambar. Saya akan menjelaskan alasannya: sebelumnya kita membahas bahwa kita tidak peduli informasi apa yang berisi setiap dimensi ruang tersembunyi. Sebuah model dapat belajar kode informasi apa pun yang dianggapnya berharga untuk tugasnya. Karena kita terbiasa dengan kumpulan data, kita tahu pentingnya dimensi, yang berisi jenis digit (yaitu nilai numeriknya). Dan sekarang kami ingin membantu model dengan memberikan informasi ini kepadanya.

Untuk jenis digit tertentu, kami langsung menyandikannya, yaitu, kami menggunakan vektor ukuran 10. Sepuluh angka ini dikaitkan dengan vektor tersembunyi, jadi ketika mendekodekan vektor ini menjadi gambar, model akan menggunakan informasi digital.

Ada dua cara untuk menyediakan model vektor pengkodean langsung:

1. Tambahkan sebagai input ke model.
2. Tambahkan sebagai label, sehingga model itu sendiri akan menghitung perkiraan: kita akan menambahkan subnet lain yang memprediksi vektor 10-dimensi, di mana fungsi kerugian adalah entropi silang dengan vektor koding forward forward yang diharapkan.

Pilih opsi kedua. Mengapa Nah, saat pengujian Anda dapat menggunakan model dalam dua cara:

1. Tentukan gambar sebagai input dan tampilkan vektor tersembunyi.
2. Tentukan vektor tersembunyi sebagai input dan hasilkan gambar.

Karena kami ingin mendukung opsi pertama, kami tidak dapat memberikan model digit sebagai input, karena kami tidak ingin mengetahuinya selama pengujian. Karena itu, model harus belajar memprediksinya.

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits 

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers']) 

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss) 

Pelatihan

Kami akan melatih model untuk mengoptimalkan dua fungsi kerugian - VAE dan klasifikasi - menggunakan SGD .

Pada akhir setiap zaman, kami memilih vektor tersembunyi dan menerjemahkannya ke dalam gambar untuk mengamati secara visual bagaimana kekuatan generatif model meningkat dari zaman. Metode pengambilan sampel adalah sebagai berikut:

1. Secara eksplisit mengatur dimensi yang digunakan untuk mengklasifikasikan berdasarkan digit yang ingin kita hasilkan. Misalnya, jika kita ingin membuat gambar angka 2, maka kita mengatur pengukuran $$$[0010000000]$.
2. Pilih secara acak dari dimensi lain dari distribusi normal multidimensi. Ini adalah nilai untuk angka yang berbeda yang dihasilkan di era ini. Jadi kita mendapatkan ide tentang apa yang dikodekan dalam dimensi lain, misalnya gaya tulisan tangan.

Arti langkah 1 adalah bahwa setelah konvergensi, model harus dapat mengklasifikasikan gambar dalam gambar input dengan pengaturan pengukuran ini. Namun, mereka juga digunakan dalam fase decoding untuk membuat gambar. Artinya, subnet decoder tahu: ketika pengukuran sesuai dengan angka 2, itu harus menghasilkan gambar dengan nomor ini. Karena itu, jika kita mengatur pengukuran secara manual ke angka 2, kita akan mendapatkan gambar yang dihasilkan dari gambar ini.

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples) 

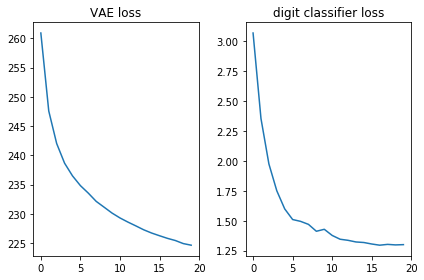
Mari kita periksa bahwa kedua fungsi kerugian terlihat baik, yaitu, mereka menurun:

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout() 

Selain itu, mari kita tampilkan gambar yang dihasilkan dan melihat apakah model benar-benar dapat membuat gambar dengan angka tulisan tangan:

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples) 

Kesimpulan

Sangat menyenangkan melihat bahwa jaringan distribusi langsung yang sederhana (tanpa kerumitan mewah) menghasilkan gambar yang indah hanya dalam 20 era. Model cepat belajar menggunakan pengukuran khusus untuk angka: di era ke-9, kita sudah melihat urutan angka yang kita coba hasilkan.

Setiap zaman menggunakan nilai acak yang berbeda untuk dimensi lain, sehingga gayanya berbeda antara era, tetapi serupa di dalamnya, setidaknya dalam beberapa. Misalnya, pada tanggal 18, semua angka lebih gemuk dibandingkan dengan tanggal 20.

Catatan

Artikel ini berdasarkan pengalaman saya dan sumber-sumber berikut:

• Kesimpulan variasi dan pembelajaran mendalam: sintesis baru
• Panduan Variasi Auto Coder