Institut Teknologi Massachusetts. Kursus Kuliah # 6.858. "Keamanan sistem komputer." Nikolai Zeldovich, James Mickens. Tahun 2014
Keamanan Sistem Komputer adalah kursus tentang pengembangan dan implementasi sistem komputer yang aman. Ceramah mencakup model ancaman, serangan yang membahayakan keamanan, dan teknik keamanan berdasarkan pada karya ilmiah baru-baru ini. Topik meliputi keamanan sistem operasi (OS), fitur, manajemen aliran informasi, keamanan bahasa, protokol jaringan, keamanan perangkat keras, dan keamanan aplikasi web.
Kuliah 1: “Pendahuluan: model ancaman”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 2: "Kontrol serangan hacker"
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 3: “Buffer Overflows: Exploits and Protection”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 4: “Pemisahan Hak Istimewa”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 5: "Dari mana sistem keamanan berasal?"
Bagian 1 /
Bagian 2Kuliah 6: “Peluang”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 7: “Kotak Pasir Klien Asli”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 8: “Model Keamanan Jaringan”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 9: "Keamanan Aplikasi Web"
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 10: “Eksekusi simbolik”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 11: “Bahasa Pemrograman Web / Web”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 12: Keamanan Jaringan
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 13: "Protokol Jaringan"
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 14: "SSL dan HTTPS"
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 15: “Perangkat Lunak Medis”
Bagian 1 /
Bagian 2 /
Bagian 3Kuliah 16: “Serangan Saluran Samping”
Bagian 1 /
Bagian 2 /
Bagian 3 Ok teman, mari kita mulai. Jadi, hari ini kita akan berbicara tentang serangan melalui saluran samping, masalah umum yang melekat pada semua jenis sistem. Dalam arti luas, serangan melalui saluran samping terjadi dalam situasi di mana Anda tidak berpikir bahwa beberapa informasi mampu mengungkapkan informasi tentang sistem Anda.
Biasanya, Anda memiliki beberapa komponen yang membuat koneksi antara pengguna dan server. Pada saat yang sama, Anda berpikir bahwa Anda tahu tentang segala sesuatu yang melewati kawat ini yang menghubungkan dua pelanggan, Anda tahu tentang semua bit yang saling dipertukarkan oleh pengguna dan server, dan ini aman. Tetapi sering terjadi bahwa beberapa informasi masih diungkapkan oleh pengguna atau server. Contoh yang dijelaskan dalam kuliah hari ini menjelaskan situasi di mana sinkronisasi pesan antara pengguna dan server mengungkapkan beberapa informasi tambahan yang tidak akan Anda ketahui, hanya dengan mengamati bit stream antara pelanggan ini.
Bahkan, ada saluran sisi kelas yang jauh lebih luas yang bisa Anda khawatirkan. Orang-orang belajar tentang penampilan saluran samping di tahun 40-an, ketika mereka menemukan bahwa jika Anda mulai mengetik karakter pada teletype, maka elektronik teletype akan mulai memancarkan radiasi frekuensi radio. Dalam hal ini, Anda dapat menempatkan osiloskop di sebelahnya dan mengamati bagaimana frekuensi sinyal radio berubah tergantung pada simbol apa yang dicetak oleh operator teletype. Dengan demikian, radiasi RF adalah contoh klasik dari saluran samping yang membuat Anda khawatir.
Ada banyak contoh lain yang diperhatikan oleh masyarakat, seperti konsumsi listrik. Ini adalah saluran sisi lain yang dapat Anda khawatirkan, karena komputer Anda akan menggunakan jumlah energi yang berbeda tergantung pada apa yang dihitungnya.
Contoh saluran samping adalah suara, karena kebocoran informasi juga dimungkinkan. Misalnya, orang mendengarkan printer dan, berdasarkan suara yang mereka buat, mereka dapat mengetahui karakter apa yang dicetaknya. Ini sangat mudah untuk printer dot matrix yang menghasilkan suara yang sangat menjengkelkan selama pencetakan.
Secara umum, ini adalah sesuatu untuk dipikirkan. Dalam ceramah hari Senin, Kevin juga menyebutkan beberapa saluran sampingan menarik yang ia bahas dalam penelitiannya. Tetapi kita akan melihat saluran samping spesifik yang dipelajari David Bramley dan Dan Bone. Dalam karya mereka, yang diterbitkan sekitar 10 tahun yang lalu, mereka menulis bahwa mereka dapat mengekstrak kunci kriptografi server web Apache dengan mengukur waktu tanggapan yang berbeda terhadap berbagai paket input dari klien yang tidak bersahabat. Dalam kasus khusus ini, mereka "berburu" untuk kunci kriptografi. Bahkan, banyak serangan melalui saluran samping menargetkan kunci kriptografi sebagian karena cukup sulit untuk mendapatkan sejumlah besar data melalui saluran tersebut. Dan kunci kriptografi adalah salah satu situasi ketika sejumlah kecil bit dikeluarkan, yaitu, selama serangan, penyerang dapat mengekstraksi sekitar 200 - 256 bit informasi. Tetapi hanya berdasarkan pada 200 bit ini, mereka dapat memecahkan kunci kriptografi server web ini.
Jika Anda mencoba masuk ke semacam basis data yang penuh dengan nomor jaminan sosial, Anda perlu "menggabungkan" banyak bit informasi darinya. Itu sebabnya sebagian besar serangan saluran samping fokus pada mendapatkan rahasia kecil seperti kunci kriptografi atau kata sandi. Tetapi secara umum, ini berlaku untuk banyak situasi lain.
Dalam materi kuliah, hal keren lainnya dijelaskan - ini semua bisa dilakukan melalui jaringan. Anda mungkin menyadari bahwa mereka harus melakukan banyak pekerjaan dengan hati-hati untuk menangkap perbedaan terkecil dalam informasi waktu ini. Setiap permintaan yang mereka kirim ke server berbeda dari permintaan lain dengan 1-2 mikrodetik, yang merupakan periode yang sangat singkat. Karena itu, Anda harus sangat berhati-hati, karena jaringan kami tidak memungkinkan kami untuk menangkap perbedaan sementara dan menentukan bahwa server telah memproses permintaan Anda untuk 1-2 mikrodetik lebih lama dari yang seharusnya.
Akibatnya, tidak jelas apakah serangan seperti itu dapat diatur dalam jaringan yang sangat "berisik", karena informasi yang berguna harus dipisahkan dari tingkat kebisingan. Orang-orang ini adalah yang pertama menunjukkan bahwa Anda benar-benar dapat melakukan ini melalui jaringan Ethernet dengan server di satu ujung jaringan dan klien di ujung lainnya. Mereka membuktikan bahwa memang mungkin untuk mengukur perbedaan-perbedaan ini sebagian dengan rata-rata, sebagian dengan trik lain.
Rencana untuk sisa kuliah ini adalah sebagai berikut - pertama kita selami rincian dari algoritma kriptografi kunci publik RSA yang digunakan orang-orang ini. Kami tidak akan mengevaluasi dari sudut pandang keamanan, tetapi kami akan melihat bagaimana penerapannya, karena ini adalah implementasi dari algoritma yang sangat penting untuk menggunakan saluran samping.
Bramley dan Bone meneliti berbagai detail implementasi untuk memahami kapan hal-hal tertentu berjalan lebih cepat atau lebih lambat. Jadi pertama-tama kita perlu mencari tahu bagaimana cryptosystem RSA diimplementasikan, dan kemudian kita akan kembali dan mencari tahu bagaimana menyerang semua struktur ini yang tersedia di RSA.
Mari kita mulai dengan meninjau RSA di tingkat tinggi. RSA adalah cryptosystem kunci publik yang cukup banyak digunakan. Kami menyebutkan orang-orang ini beberapa minggu yang lalu ketika kami berbicara tentang sertifikat. Sekarang kita akan melihat bagaimana cara kerjanya.
Biasanya, ada 3 hal yang perlu Anda khawatirkan - ini adalah pembuatan kunci, enkripsi dan dekripsi. Di RSA, cara untuk membuat kunci adalah dengan memilih 2 bilangan bulat besar, dilambangkan dengan p dan q. Dalam artikel mereka, orang-orang ini menulis tentang p dan q masing-masing dengan ukuran 512 bit. Ini biasanya disebut RSA 1024-bit, karena produk bilangan prima ini adalah bilangan bulat 1000-bit. Saat ini, ini mungkin bukan pilihan yang baik untuk ukuran kunci RSA, karena memecahnya adalah tugas yang relatif mudah bagi penyerang. Jadi jika 10 tahun yang lalu 1000 bit sepertinya jumlah yang masuk akal, hari ini ketika membangun sebuah sistem, Anda harus memilih 2000, 3000 atau bahkan 4000 bit kunci RSA. Jadi ukuran kunci RSA berarti ukuran bilangan prima ini.
Kemudian, untuk kenyamanan, kita akan berbicara tentang angka n, yang merupakan produk dari bilangan prima ini n = pq, dan angka ini disebut modul. Jadi sekarang kita tahu cara membuat kunci, atau setidaknya bagian dari kunci, kita harus mencari cara untuk mengenkripsi dan mendekripsi pesan.
Dan cara kita akan mengenkripsi dan mendekripsi pesan didasarkan pada peningkatan kekuatan angka modulo. Tampaknya sedikit aneh, tetapi kami akan mencari tahu dalam hitungan detik. Jadi, jika Anda ingin mengenkripsi pesan m, Anda harus mengonversinya ke pesan oleh mod n. Nilai e adalah gelar, dalam sedetik kita akan mencari tahu bagaimana memilihnya. Beginilah cara kita mengenkripsi pesan.
Yaitu, kami hanya menerima pesan ini sebagai bilangan bulat dan menaikkannya menjadi kekuatan. Sebentar lagi kita akan melihat mengapa ini berhasil, tetapi untuk sekarang, kami akan menyatakan semua pesan terenkripsi ini dengan huruf C.
Kemudian, untuk mendekripsinya, kita harus menemukan eksponen lain yang menarik, yang memungkinkan kita untuk mengambil pesan terenkripsi C, menaikkannya ke daya d modulo, dan sebagai hasilnya, secara ajaib mendapatkan pesan yang didekripsi m.
Jadi, prinsip umum adalah menggunakan satu eksponen untuk mengenkripsi pesan dan eksponen lain untuk mendekripsi.
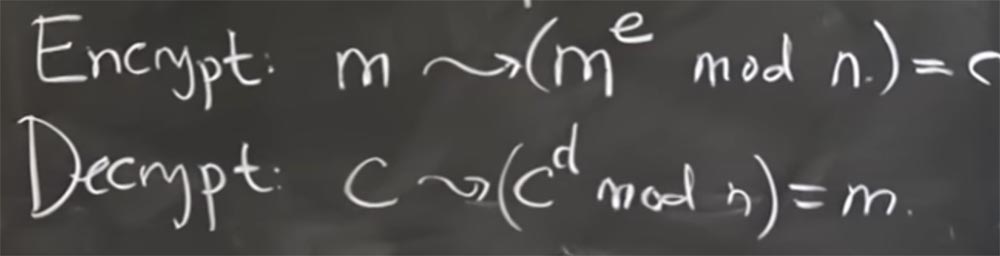
Secara keseluruhan, tampaknya agak sulit untuk memahami bagaimana kita akan menghasilkan dua angka ajaib yang entah bagaimana mengembalikan kita pesan aslinya. Tetapi jika Anda melihat bagaimana modul eksponensial atau multiplikasi nomor ini bekerja, maka Anda akan mengerti segalanya.
Jika kita mengambil X dan menaikkannya ke daya yang sama dengan fungsi φ dari n, maka ini akan menjadi 1 modulo n:
X
φ (n) = 1 mod n
Fungsi phi ini untuk pilihan n khusus kita cukup sederhana, sama dengan φ = (p-1) (q-1).
Maka produk dari eksponen terbuka, yang lebih besar dari 1 tetapi kurang dari φ (n), oleh eksponen rahasia d, akan sama dengan:
ed = ɑφ (n) +1, dengan ɑ adalah konstanta.
Dengan demikian, dimungkinkan untuk mendekripsi pesan dengan benar, karena ada algoritma yang cukup sederhana jika Anda mengetahui nilai φ (n) untuk menghitung d dengan mempertimbangkan e atau e dengan memperhitungkan d.
Pemirsa: Apakah 1 modulo n tidak sama dengan 1?
Profesor: ya, saya membuat kesalahan di sini, kesetaraan akan terlihat seperti ini:
X
φ (n) mod n = 1 mod n, yaitu nilai X dalam derajat fungsi "fi" dari n modulo n sama dengan modulity n kesatuan.
Ini pada dasarnya berarti bahwa untuk RSA kita harus memilih beberapa nilai e, yang akan menjadi nilai enkripsi kita. Kemudian dari e kita akan menghasilkan d berdasarkan rumus de = 1 mod φ (n), maka d = 1 / e mod φ (n).
Ada beberapa algoritma Euclidean yang dapat Anda gunakan secara efektif untuk perhitungan ini. Tetapi untuk melakukan ini, Anda harus mengetahui ini φ (n), yang membutuhkan faktorisasi, yaitu, faktorisasi angka kita n menjadi faktor p dan q.
Jadi, RSA adalah sistem di mana kunci publik adalah pasangan: eksponen enkripsi e dan angka n, dan pasangan d dan n adalah kunci pribadi yang dirahasiakan. Jadi siapa pun dapat meningkatkan kekuatan untuk mengenkripsi itu untuk Anda. Tetapi hanya Anda yang tahu nilai d ini dan oleh karena itu Anda dapat mendekripsi pesan tersebut. Dan sampai Anda mengetahui faktorisasi dari faktor-faktor P dan Q, atau N ini, sama dengan produk P dan Q, Anda tidak tahu apa φ = (p-1) (q-1).
Akibatnya, menghitung nilai d ini adalah tugas yang agak sulit. Inilah yang dimaksud dengan algoritma RSA tingkat tinggi.
Sekarang kita sudah terbiasa dengan prinsip-prinsip RSA, saya ingin memikirkan 2 hal. Ada trik tentang cara menggunakannya dengan benar dan ada jebakan yang muncul saat menggunakannya. Ada banyak cara untuk mengimplementasikan kode untuk eksponensial ini dan melakukannya secara efisien. Ini adalah tugas yang agak luar biasa, karena kita berurusan dengan bilangan bulat 1000-bit, di mana Anda tidak bisa hanya menjalankan instruksi perkalian. Mungkin akan memakan waktu lama untuk menyelesaikan operasi ini.
Karena itu, hal pertama yang ingin saya sebutkan adalah berbagai perangkap RSA. Salah satunya adalah multiplisitas. Misalkan kita memiliki 2 pesan: m
0 dan m
1 . Saya akan mengenkripsi mereka, mengubah m
0 menjadi m
0 e mod n, dan m1 menjadi m
1 e mod n. Masalah yang mungkin terjadi, atau lebih tepatnya, bukan masalah, tetapi kejutan yang tidak menyenangkan bagi seseorang yang menggunakan RSA adalah bahwa sangat mudah untuk mengenkripsi produk m
0 dengan m
1 , karena Anda cukup mengalikan 2 digit ini: m
0 e mod n * m
1 e mod n.
Jika Anda mengalikannya, Anda akan mendapatkan produk (m
0 m
1 )
dan modul. Ini adalah enkripsi yang benar dengan penggunaan RSA yang disederhanakan untuk nilai m
0 m
1 . Ini bukan masalah besar saat ini, karena Anda dapat dengan mudah membuat pesan terenkripsi ini, tetapi Anda tidak dapat mendekripsi pesan itu. Namun, ada kemungkinan bahwa sistem umum akan memungkinkan Anda untuk mendekripsi pesan tertentu. Yaitu, jika memungkinkan Anda untuk mendekripsi pesan yang Anda buat, maka mungkin dengan mengikuti jalur sebaliknya, Anda dapat mengetahui apa pesan-pesan ini adalah m
0 dan m
1 .
Fakta ini tidak boleh diabaikan, karena mempengaruhi sejumlah protokol menggunakan RSA. Ada satu properti yang akan kita gunakan sebagai mekanisme pertahanan di akhir kuliah kita.
Perangkap kedua, atau properti RSA, yang harus Anda perhatikan adalah determinisme, atau determinabilitas. Dalam implementasi dasar yang dijelaskan sebelumnya, jika Anda mengambil pesan dan mengenkripsi pesan, mengubahnya menjadi mod, maka ini adalah fungsi pesan deterministik. Karena itu, jika Anda mengenkripsi lagi, Anda akan mendapatkan enkripsi yang sama persis.
Ini bukan properti yang diinginkan, karena jika saya melihat bahwa Anda mengirim beberapa pesan yang dienkripsi menggunakan RSA dan saya ingin tahu apa itu, mungkin sulit bagi saya untuk mendekripsi. Tetapi saya dapat mencoba hal-hal yang berbeda, akibatnya saya melihat bahwa Anda mengirim pesan ini.
Kemudian saya akan mengenkripsi dan melihat apakah Anda mendapatkan teks terenkripsi yang sama. Dan jika demikian, maka saya akan mengetahui bahwa Anda telah mengenkripsi. Karena semua yang saya butuhkan untuk mengenkripsi pesan adalah kunci publik yang dapat diakses publik, yang merupakan sepasang angka (n, e).
Jadi ini tidak terlalu bagus, dan Anda mungkin harus berhati-hati dengan properti ini saat menggunakan RSA. Dengan demikian, primitif jenis ini sulit digunakan secara langsung.
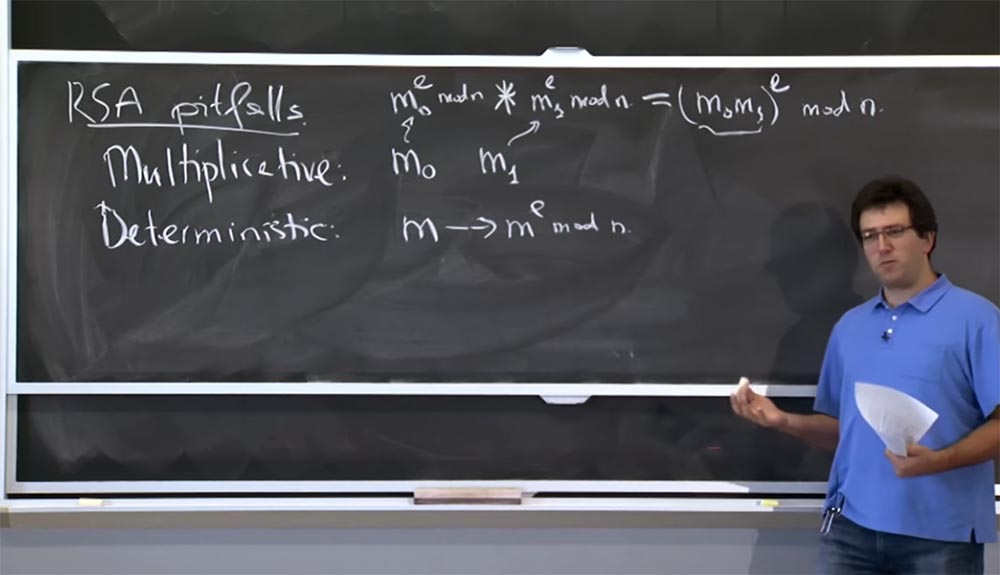
Dalam praktiknya, untuk menghindari masalah serupa dengan RSA, orang menyandikan pesan dengan cara tertentu sebelum enkripsi. Alih-alih langsung mengangkat pesan ke kekuatan, mereka mengambil semacam fungsi pesan dan menaikkannya ke modul daya:
(f (m))
e mod n.
Fungsi f ini, yang umum digunakan saat ini, disebut OAEP - Optimal Asymmetric Encryption with Addition. Ini adalah sesuatu yang dikodekan dengan dua properti menarik.
Pertama, ini membawa keacakan. Anda dapat menganggap f (m) sebagai menghasilkan pesan 1000-bit yang akan Anda enkripsi. Bagian dari pesan ini akan menjadi pesan Anda di sini di tengah-tengah kotak ini. Tentu saja, Anda bisa mendapatkannya kembali ketika mendekripsi. Jadi, ada 2 hal menarik yang ingin Anda lakukan: di sebelah kanan Anda menempatkan beberapa jenis keacakan, nilai r. Ini memberikan bahwa jika Anda mengenkripsi pesan beberapa kali, Anda akan mendapatkan hasil yang berbeda setiap kali, sehingga enkripsi tidak akan lagi ditentukan.
Untuk mengatasi properti multiplikasi ini dan jenis masalah lainnya, di sebelah kiri Anda memiliki pad pad, yang merupakan urutan tipe 1 0 1 0 1 0. Anda dapat memilih urutan yang lebih baik, tetapi secara kasar, ini adalah semacam urutan yang dapat diprediksi, yang Anda menyisipkan di sini dan kapan pun Anda mendekripsi pesan, Anda memastikan bahwa urutan ini masih ada. Multiplicativeness akan menghancurkan bit pad ini, dan kemudian akan menjadi jelas bagi Anda bahwa seseorang mengacaukan pesan Anda dan membuangnya. Jika bit-bit ini tetap di tempatnya, ini membuktikan bahwa tidak ada yang memalsukan pesan Anda dan Anda dapat menerimanya, karena itu dienkripsi dengan benar oleh seseorang.
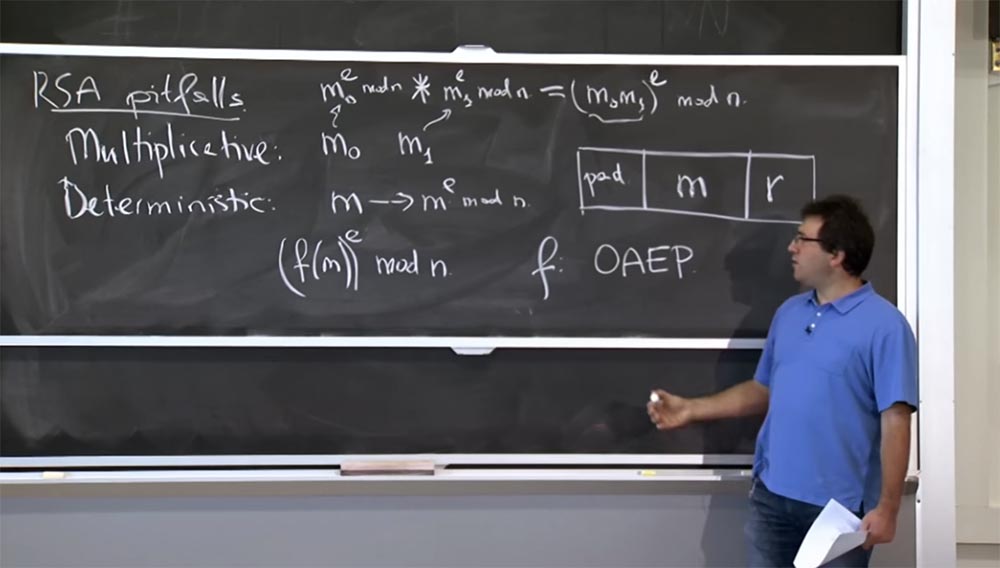Audiens: jika seorang penyerang tahu seberapa besar nilai pad, dapatkah ia menetapkan 1 ke bagian paling bawah dari urutan dan kemudian mengalikan nilai itu?
Profesor: ya, mungkin. Ini agak rumit, karena keacakan ini akan berlanjut. Jadi desain spesifik dari OAEP ini sedikit lebih rumit daripada yang saya gambarkan. Tapi bayangkan ini adalah perkalian bilangan bulat bukan multiplikasi, keacakan memperluas lebih jauh, sehingga Anda dapat membuat skema OAEP di mana ini tidak akan terjadi.
Ternyata Anda seharusnya tidak menggunakan matematika RSA ini secara langsung, dalam praktiknya Anda harus menggunakan semacam perpustakaan yang mengimplementasikan semua hal ini untuk Anda dengan cara yang benar, dan menggunakannya sebagai parameter enkripsi dan dekripsi.
Namun, perincian yang dibahas di atas akan bermanfaat bagi kami, karena kami sebenarnya sedang mencoba mencari cara untuk menghancurkan atau menyerang implementasi RSA yang ada.
Secara khusus, serangan yang dijelaskan dalam artikel kuliah akan memanfaatkan fakta bahwa server akan menguji add-on pading ini ketika menerima pesan. Jadi ini adalah bagaimana kita akan mempertimbangkan waktu yang diperlukan server untuk mendekripsi. Kami akan mengirim pesan yang dibuat dengan hati-hati, tetapi pesan itu tidak dibuat dari pesan asli dan enkripsinya. Kami akan membuat nilai integer terenkripsi yang menyeluruh.
Server akan mencoba mendekripsi dan akan mendapatkan semacam absurditas, yang mana pad pad kemungkinan besar tidak akan dipasangkan, dan server akan segera menolak pesan ini. , , , , : RSA, , . , . , .
, , RSA. , , , . , , , 1000 . e .
, . , 1000 . 1000- , 1000 1000 n, . RSA , .
4 , . , . , CRT. . . , , , , [ = a
1 ] mod p [ = a
2 ] mod q, q – , .
, [ =
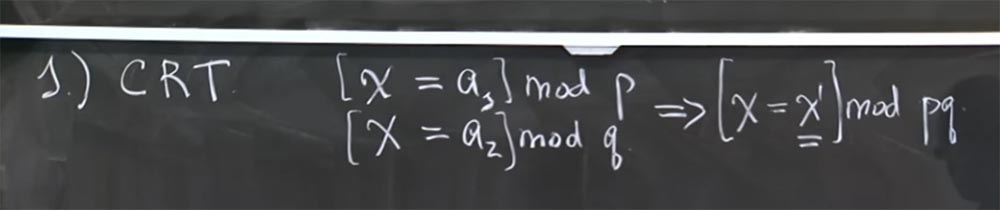
1 ] mod pq.
1 , .
1 , mod pq a
1 a
2 mod p q.
, ? , , n, p q.
, mod pq, mod p mod q. , , mod pq. , ? , , ?
: , ?
: , , , . , p q, n 1000 , p q 500 , . , , — , , . — . , , . 1000 512 , 2 . , 4 . [ = a
1 ] mod p [ = a
2 ] mod q , 4 . 2 RSA , .
, .
, Sliding windows, « ». . , .
, - , 500 , mod p mod q, d. c d? , c d . d , 500, . , , . , « ». .
c
2x , : (c
x )
2 :
c
2x = (c
x )
2c
2x , 2 , cx, . , , c
2x+1 :
c
2x+1 = (c
x )
2 x
.
, , , . , , , . , .
« », ? , . , , « » c
2x+1 = (c
x )
2 x .
, , , – , c
2x+1 c
2x , c. , , . , .
, :
1
3
7
...
31
. , , , .
,
32x+y , 5 , 32- ,
y .
32 . , , , , c . «» .
29:00
Kursus MIT "Keamanan Sistem Komputer". Kuliah 16: Serangan Melalui Saluran Samping, Bagian 2Versi lengkap dari kursus ini tersedia di sini .Terima kasih telah tinggal bersama kami. Apakah Anda suka artikel kami? Ingin melihat materi yang lebih menarik? Dukung kami dengan melakukan pemesanan atau merekomendasikannya kepada teman-teman Anda,
diskon 30% untuk pengguna Habr pada analog unik dari server entry-level yang kami temukan untuk Anda: Seluruh kebenaran tentang VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps dari $ 20 atau bagaimana membagi server? (opsi tersedia dengan RAID1 dan RAID10, hingga 24 core dan hingga 40GB DDR4).
VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps hingga Desember secara gratis ketika membayar untuk jangka waktu enam bulan, Anda dapat memesan di sini .Dell R730xd 2 kali lebih murah? Hanya kami yang memiliki
2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV dari $ 249 di Belanda dan Amerika Serikat! Baca tentang
Cara Membangun Infrastruktur Bldg. kelas menggunakan server Dell R730xd E5-2650 v4 seharga 9.000 euro untuk satu sen?