Kursus MIT "Keamanan Sistem Komputer". Kuliah 16: Serangan Melalui Saluran Samping, Bagian 2

Institut Teknologi Massachusetts. Kursus Kuliah # 6.858. "Keamanan sistem komputer." Nikolai Zeldovich, James Mickens. Tahun 2014

Keamanan Sistem Komputer adalah kursus tentang pengembangan dan implementasi sistem komputer yang aman. Ceramah mencakup model ancaman, serangan yang membahayakan keamanan, dan teknik keamanan berdasarkan pada karya ilmiah baru-baru ini. Topik meliputi keamanan sistem operasi (OS), fitur, manajemen aliran informasi, keamanan bahasa, protokol jaringan, keamanan perangkat keras, dan keamanan aplikasi web.

Kuliah 1: “Pendahuluan: model ancaman” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 2: "Kontrol serangan hacker" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 3: “Buffer Overflows: Exploits and Protection” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 4: “Pemisahan Hak Istimewa” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 5: "Dari mana sistem keamanan berasal?" Bagian 1 / Bagian 2
Kuliah 6: “Peluang” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 7: “Kotak Pasir Klien Asli” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 8: “Model Keamanan Jaringan” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 9: "Keamanan Aplikasi Web" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 10: “Eksekusi simbolik” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 11: “Bahasa Pemrograman Web / Web” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 12: Keamanan Jaringan Bagian 1 / Bagian 2 / Bagian 3
Kuliah 13: "Protokol Jaringan" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 14: "SSL dan HTTPS" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 15: “Perangkat Lunak Medis” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 16: “Serangan Saluran Samping” Bagian 1 / Bagian 2 / Bagian 3

Audiens: bagaimana menentukan x dan y terlebih dahulu?

Profesor: untuk ini, Anda harus melihat peserta dalam representasi biner. Misalkan saya mencoba menghitung nilai c ^1011010 , derajatnya juga dapat terdiri dari jumlah bit yang lebih besar. Jika kita ingin melakukan kuadrat ulang, maka kita perlu melihat bit terendah - ini dia 0.



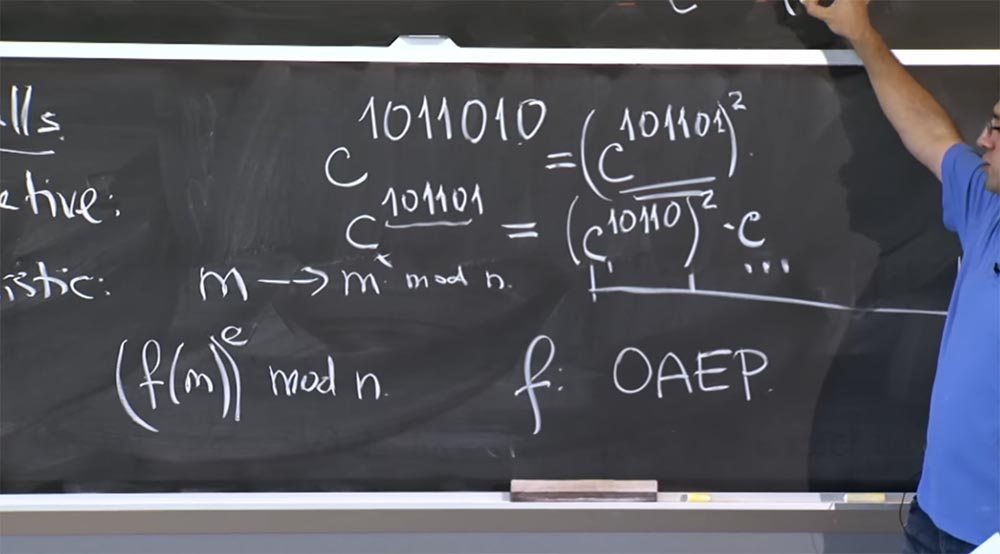
Dengan demikian, kita mendapatkan persamaan c ^1011010 = (c ¹⁰¹¹⁰¹ ) ²

Selanjutnya, kita perlu menghitung c ¹⁰¹¹⁰¹ , di sini kita tidak dapat menggunakan aturan ini, karena ini bukan 2x - itu akan menjadi x plus 1. Oleh karena itu, kita menulis persamaan ini:

c ¹⁰¹¹⁰¹ = (c ¹⁰¹¹⁰ ) ² c, karena awalan ini 101101 = 10110 +1.

Oleh karena itu, kita mengalikan kuadrat dengan c, jadi kami menggunakannya untuk kuadrat ulang.

Untuk "sliding windows" kita perlu menangkap lebih banyak bit dari ujung bawah. Jika Anda ingin melakukan trik di sini dengan "jendela geser" alih-alih mengekstraksi satu dari sini, maka dengan memperhitungkan tabel besar ini, kami dapat mengambil 3 bit sekaligus, menempel pada c7. Jika kita mengambil 3 bit pertama dari sebuah gelar, kita mendapatkan c ¹⁰¹¹⁰¹ = (c ¹⁰¹ ) ⁸ c ¹⁰¹ .

Dalam hal ini, kami benar-benar memiliki jumlah perhitungan yang sama untuk (c ¹⁰¹ ) ⁸ , tetapi Anda dapat melihat nilai c ¹⁰¹ dalam tabel. Dan bagian dalam bentuk (c ¹⁰¹ ) ⁸ mengatakan bahwa Anda akan menggunakan "jendela geser" untuk menghitung nilainya.



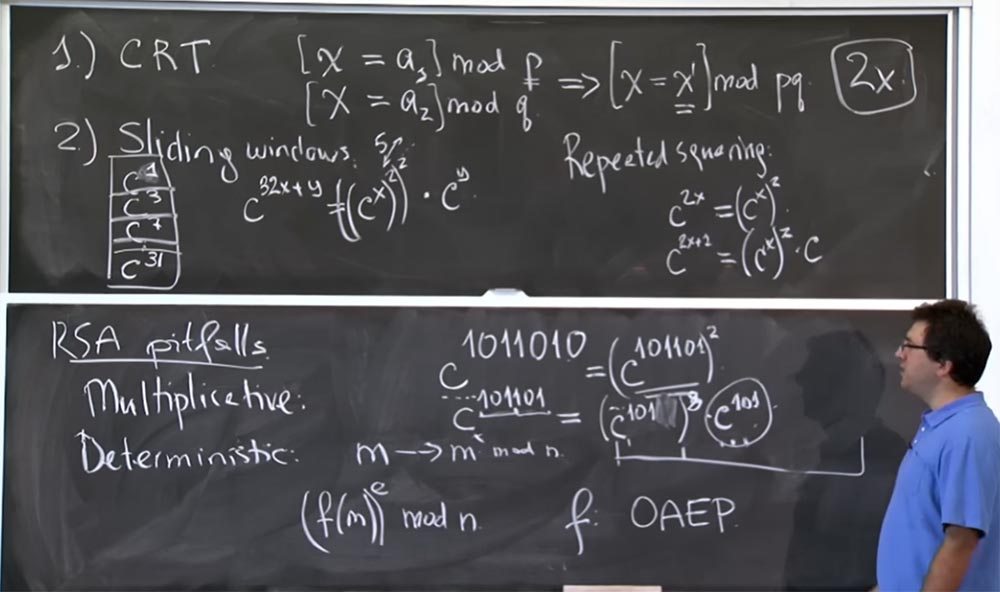
Ini menghemat banyak waktu, karena memungkinkan untuk menggunakan nilai pra-dikalikan. 10 tahun yang lalu diyakini bahwa tabel nilai hingga 32 derajat adalah rencana optimal dalam hal efisiensi komputasi, karena ada beberapa jenis kompromi di sini, kan? Anda menghabiskan waktu membuat tabel ini, tetapi itu tidak boleh terlalu besar jika Anda tidak akan sering menggunakan beberapa catatan. Misalkan jika Anda membuat tabel nilai hingga c ⁵⁰⁰ derajat, tetapi Anda tidak akan menggunakan eksponen dengan nilai lebih dari 128, maka buang saja waktu Anda.

Hadirin: apakah ada alasan untuk tidak membuat meja sebesar itu sebelumnya? Yaitu, untuk menghitung nilai-nilai sejumlah derajat yang dapat dielakkan dalam perhitungan?

Profesor: jika Anda tidak ingin melakukan perhitungan volumetrik terlebih dahulu ... well, ada dua hal. Salah satunya adalah bahwa Anda harus memiliki kode untuk memeriksa apakah catatan yang diperlukan dalam tabel penuh atau tidak, dan ini mungkin akan mengurangi akurasi memprediksi cabang-cabang proses CPU. Pada saat yang sama, dalam kasus umum, prosesor akan bekerja lebih lambat, karena harus memeriksa apakah catatan yang diperlukan ada di dalam tabel. Hal kedua, yang agak menjengkelkan, bisa jadi bocoran entri tabel melalui berbagai saluran samping, yaitu melalui pola akses cache. Jadi, jika Anda memiliki beberapa proses lain yang berjalan pada prosesor yang sama, Anda dapat melihat alamat cache mana yang dihapus dari cache atau diperlambat karena seseorang memiliki akses untuk merekam c ³ atau untuk merekam c ³¹ . Dan semakin besar tabel ini, semakin mudah untuk menentukan bit eksponen mana yang digunakan untuk membuat kunci RSA.

Tabel raksasa ini dapat memberi tahu alamat cache mana yang hilang untuk prosesor, yaitu, menunjukkan bahwa proses enkripsi harus memiliki akses ke entri ini dalam tabel. Pada gilirannya, ini memberitahu Anda bahwa urutan bit yang diberikan muncul dalam eksponen kunci pribadi Anda. Oleh karena itu, saya berasumsi bahwa secara matematis Anda dapat mengisi tabel ini sebanyak yang diperlukan, tetapi dalam praktiknya Anda tidak ingin hasilnya berubah menjadi ukuran raksasa. Selain itu, Anda tidak akan dapat menggunakan entri tabel besar secara efektif. Jauh lebih bermanfaat untuk menggunakan catatan dari tabel yang relatif kecil berulang kali, misalnya, untuk menghitung c ⁷ Anda dapat menggunakan nilai c ³ dua kali dan seterusnya.

Jadi, berikut adalah optimasi RSA dengan mengkuadratkan kembali dan metode “sliding window”. Saya tidak tahu apakah mereka masih menggunakan ukuran "jendela geser" ini, tetapi dalam hal apa pun itu mempercepat proses perhitungan, karena jika tidak, Anda harus membuat kuadrat setiap bit eksponen dan kemudian dikalikan dengan setiap bit. Oleh karena itu, jika Anda memiliki eksponen 500-bit, maka Anda harus menyelesaikan 500 kotak dan sekitar 256 perkalian dengan c. Dengan "sliding windows" Anda masih harus membuat 512 kotak, karena ini tidak dapat dihindari, tetapi jumlah perkalian dengan c akan berkurang dari 256 menjadi sekitar 32 karena penggunaan entri dari tabel.

Ini adalah rencana optimalisasi umum, yang mempercepat proses perhitungan sekitar satu setengah kali. Ini adalah optimasi yang cukup sederhana. Ada dua trik pintar dengan angka yang membuat proses multiplikasi lebih efisien.

Yang pertama adalah transformasi Montgomery, sebentar lagi kita akan melihat mengapa ini sangat penting bagi kita. Optimalisasi ini mencoba memecahkan masalah bagi kami, yaitu setiap kali kami melakukan perkalian, kami mendapatkan angka yang terus tumbuh dan tumbuh dalam urutan yang meningkat. Secara khusus, di kedua “jendela geser” dan dalam mengkuadratkan kembali, Anda sebenarnya mengalikan 2 angka bersamaan ketika Anda menaikkan c ke kekuatan y.

Masalahnya adalah bahwa jika data input c ^x dan c ^y untuk perkalian, katakanlah, masing-masing 512 bit, maka ukuran hasil perkalian akan menjadi 1000 bit. Setelah itu, Anda mengambil hasil 1000-bit ini dan sekali lagi mengalikannya dengan sesuatu seperti 512 bit, itu menjadi ukuran 1500, 2000, 2500 bit dan semuanya tumbuh dan tumbuh.

Namun, Anda tidak menginginkan ini, karena perkalian meningkatkan urutan angka yang dikalikan. Karena itu, kita harus menjaga ukuran angka kita sekecil mungkin, pada dasarnya sama dengan 512 bit, karena semua perhitungan ini adalah mod p atau mod q.

Kita dapat mengurangi angka ini, katakanlah, kita ingin menghitung (((c ^x ) ² ) ² ) ² . Apa yang bisa Anda lakukan adalah, misalnya, menghitung cx modulo p, lalu kuadratkan lagi modulo p dan sekali lagi kuadrat modulo p. Metode ini relatif baik, karena memungkinkan kita untuk menjaga ukuran angka kita dalam 512 bit, yaitu, sekecil yang kita dapat. Ini bagus dalam arti mengurangi ukuran angka yang perlu kita kalikan, tetapi pada kenyataannya, operasi dengan modul ini p secara signifikan “meningkatkan biaya” perhitungan.



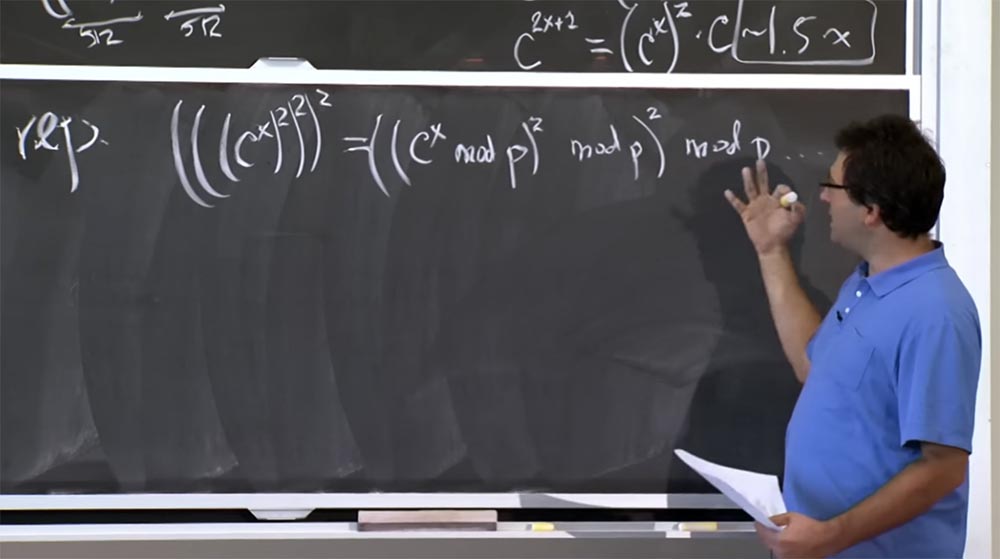
Karena cara Anda mendapatkan mod p ada di divisi. Dan pembagian lebih buruk daripada multiplikasi. Saya tidak akan mencantumkan algoritma untuk pembagian, tetapi sangat lambat. Biasanya Anda mencoba menghindari operasi divisi bila memungkinkan, karena ini bukan pemrograman yang mudah. Faktanya adalah bahwa Anda perlu menggunakan semacam algoritma perkiraan, metode Newton dan sejenisnya, dan semua ini akan memperlambat proses perhitungan.

Perkalian jauh lebih menguntungkan, tetapi menggunakan mod p atau operasi mod q untuk mengurangi ukuran angka akan lebih mahal daripada perkalian. Saya akan menunjukkan kepada Anda cara untuk menghindari ini dan bagaimana melakukan perhitungan cepat menggunakan transformasi Montgomery.

Ide dasarnya adalah untuk merepresentasikan bilangan bulat yang akan Anda gandakan dalam bentuk transformasi Montgomery. Ini sebenarnya sangat mudah. Untuk melakukan ini, kita cukup gandakan nomor kita dengan nilai magis tertentu R. Setelah sedetik aku akan memberitahumu apa itu. Tapi pertama mari kita cari tahu apa yang terjadi ketika kita memilih nilai sewenang-wenang dari R.

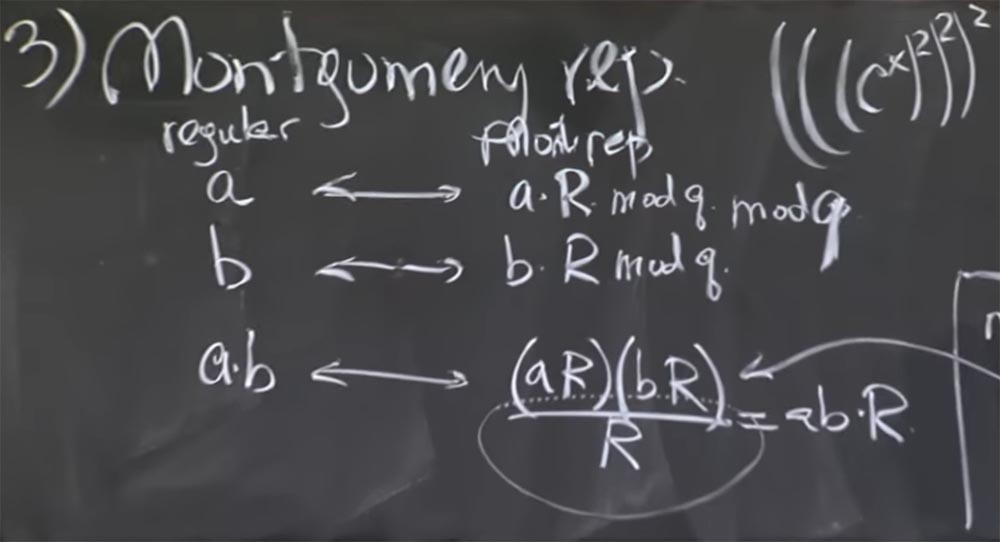
Jadi, kita mengambil 2 angka, a dan b, dan mengubahnya menjadi representasi Montgomery, mengalikan masing-masing dengan R. Kemudian produk dari a dan b dalam transformasi Montgomery akan terlihat seperti ini:

ab <-> (aR) (bR) / R = abR

Artinya, Anda kalikan aR dengan bR dan dapatkan produk ab dengan R kuadrat. Sekarang kami memiliki dua Rs, ini sedikit menyebalkan, tetapi Anda dapat membaginya dengan R. Sebagai hasilnya, kami mendapatkan produk ab oleh R. Ini agak tidak jelas mengapa kami perlu melipatgandakan angka ini sekali lagi. Pertama mari kita cari tahu apakah ini benar, dan kemudian kita akan mengerti mengapa ini akan lebih cepat.
Ini benar dalam arti sangat mudah. Jika Anda ingin mengalikan beberapa angka, maka Anda perlu mengalikannya dengan nilai R ini dan mendapatkan transformasi Montgomery. Setiap kali kita mengalikan 2 angka ini, kita harus membaginya dengan R, dan kemudian melihat bentuk transformasi dari bentuk abR. Kemudian, ketika kita selesai mengkuadratkan, mengalikan, dan semua hal ini, kita akan kembali ke bentuk normal, hasil normal, cukup membaginya dengan R untuk yang terakhir kalinya.



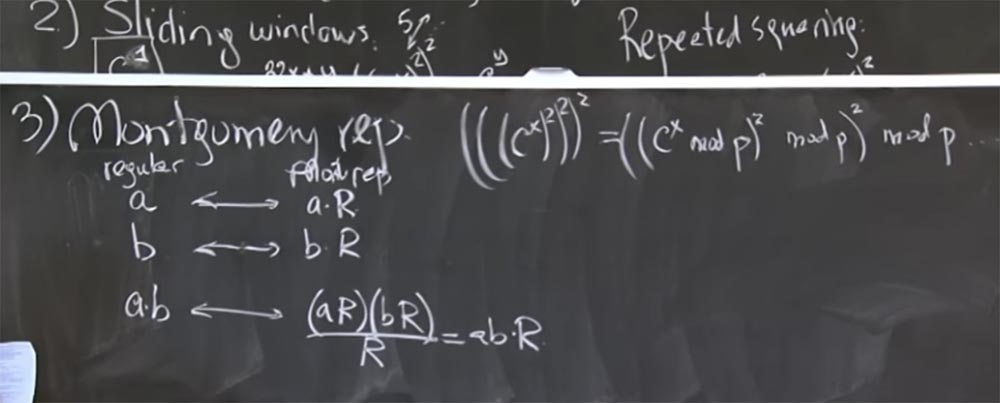
Sekarang pertimbangkan bagaimana memilih nomor yang paling cocok untuk R untuk membuat pembagian dengan R operasi yang sangat cepat. Dan hal paling keren di sini adalah jika pembagian oleh R sangat cepat ketika jumlahnya kecil, dan kita tidak perlu melakukan mod q ini terlalu sering. Secara khusus, aR, katakanlah, juga akan memiliki ukuran sekitar 500 bit, karena semua ini sebenarnya adalah mod p atau mod q. Jadi, aR adalah 500 bit, bR juga akan menjadi 500 bit, sehingga produk (aR) (bR) akan menjadi 1000 bit. R juga akan menjadi angka 500-bit yang nyaman, ukuran p. Dan jika kita bisa membuat operasi divisi cukup cepat, maka hasil ab juga akan menjadi sekitar angka 500-bit, sehingga kita dapat berkembang biak tanpa perlu divisi tambahan. Membagi dengan R jauh lebih menguntungkan dan memberi kita hasil yang kecil, yang menghindari penggunaan mod p dalam kebanyakan situasi.

Jadi apa nomor R aneh yang saya bicarakan ini sepanjang waktu? Ini memiliki nilai 2 hingga 512 derajat:

R = 2 ⁵¹²

Ini akan menjadi 1 dan sekelompok nol, sehingga mudah untuk dikalikan dengan angka seperti itu, karena itu cukup dengan hanya menambahkan sekelompok nol pada hasilnya. Pembagian juga bisa sederhana jika bit paling tidak signifikan dari hasilnya adalah nol. Jadi jika Anda memiliki nilai dari tumpukan bit yang disertai dengan 512 nol, maka membaginya dengan 2 hingga 512 derajat akan sangat sederhana - Anda hanya menjatuhkan nol di sisi kanan, dan ini adalah operasi pembagian yang sepenuhnya benar.

Masalah kecilnya adalah bahwa kita sebenarnya tidak memiliki angka nol di sisi kanan ketika Anda melakukan perkalian ini. Kami memiliki angka 512-bit nyata menggunakan semua 512 bit.

Produk dari (aR) oleh (bR) juga merupakan bilangan real dari urutan 1000 bit, jadi kita tidak bisa hanya menjatuhkan bit yang paling tidak signifikan. Tetapi pendekatan yang masuk akal didasarkan pada fakta bahwa satu-satunya hal yang membuat kita khawatir adalah nilai dari mod p. Dengan demikian, Anda selalu dapat menambahkan beberapa p ke nilai ini tanpa mengubah setara mod p-nya. Sebagai hasilnya, kita dapat menambahkan beberapa nilai p sehingga semua bit yang paling tidak signifikan menjadi nol. Mari kita lihat beberapa contoh sederhana. Saya tidak akan menulis 512 bit di papan tulis, tetapi saya hanya akan memberikan contoh singkat.

Misalkan dalam situasi kita R = 2 ⁴ = 10000. Ini adalah ukuran yang jauh lebih kecil daripada yang sebenarnya. Mari kita lihat bagaimana transformasi Montgomery ini bekerja. Kami mencoba menghitung mod q, di mana q = 7. Dalam bentuk biner q = 7 adalah (111).

Misalkan lebih jauh kita melakukan beberapa perkalian (aR) (bR), dan dalam representasi biner hasilnya adalah 11010, yaitu, ini akan menjadi nilai produk (aR) (bR). Bagaimana kita membaginya dengan R?

Jelas, tidak semua empat bit paling signifikan adalah nol, jadi kita tidak bisa hanya memisahkannya, tetapi kita dapat menambahkan jumlah yang merupakan kelipatan q. Secara khusus, kita dapat menambahkan 2 kali dalam q, dengan 2q = 1110 dalam representasi biner. Sebagai hasil dari penambahan, kami mendapatkan 101000, saya harap saya melakukan semuanya dengan benar.



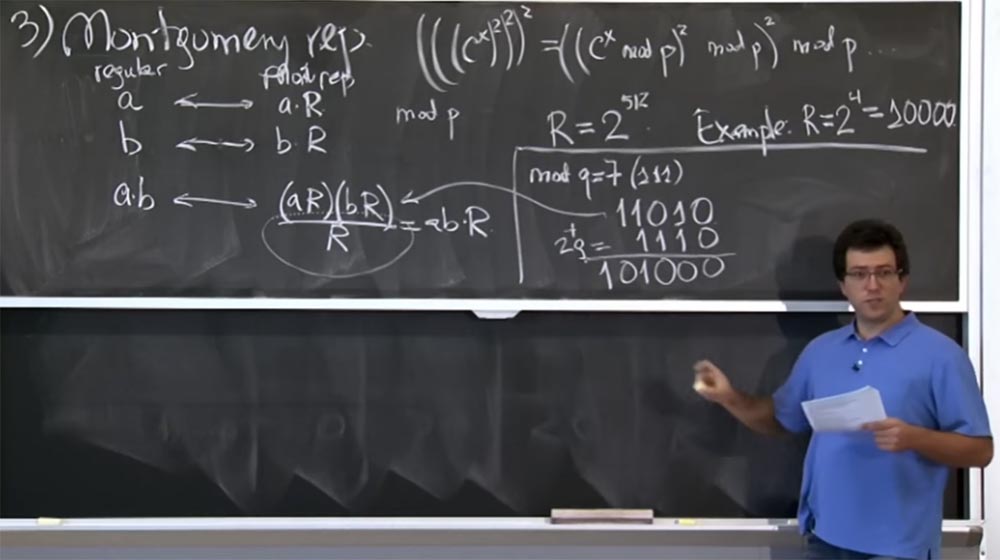
Jadi kami mendapat jumlah (aR) (bR) + 2q. Faktanya, kami tidak peduli +2q, karena yang kami pedulikan hanyalah nilai mod q. Sekarang kita lebih dekat ke tujuan, karena kita memiliki tiga nol di sebelah kanan. Sekarang kita dapat menambahkan beberapa q lagi. Katakanlah saat ini akan menjadi 8q, yang akan menjadi 111000. Sekali lagi, tambahkan baris kami dan dapatkan 1100000. Sekarang kita memiliki yang asli (aR) (bR) + 2q + 8q = 1100000. Akhirnya, kita dapat dengan mudah membagi hal ini menjadi R, hanya menjatuhkan empat nol rendah.



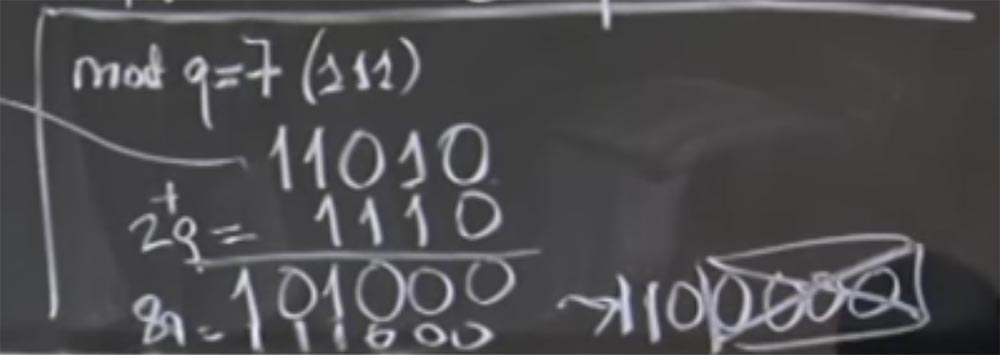Pemirsa: produk (aR) (bR) akan selalu berakhir dengan 1024 nol?

Profesor: tidak, dan saya akan menjelaskan apa yang bisa menjadi kebingungan. Katakanlah angka a adalah 512 bit, kita mengalikannya dengan R dan mendapat angka 1000-bit. Dalam hal ini, Anda benar, aR adalah angka di mana bit tinggi adalah a, dan bit rendah semuanya nol. Tapi kemudian kita jalankan mod q untuk membuatnya lebih kecil. Oleh karena itu, ukuran 1024 bit dalam kasus umum adalah kecelakaan, karena angka ini hanya memiliki nol rendah selama konversi pertama, tetapi setelah Anda melakukan beberapa penggandaan, itu akan menjadi bit acak.

Agar tidak menyesatkan Anda, saya harus menulis mod q di sini setelah aR dan setelah bR - di sini saya menambahkannya - dan menghitung mod q ini segera setelah Anda melakukan konversi untuk mengurangi nilai.



Konversi awal agak melelahkan, atau paling tidak semahal modulasi konvensional dalam multiplikasi. Yang keren adalah Anda membayar harga ini satu kali ketika Anda melakukan konversi Montgomery, dan kemudian, alih-alih mengubahnya kembali pada setiap langkah perhitungan, Anda hanya menyimpannya dalam bentuk tampilan Montgomery.
Ingat bahwa untuk meningkatkan daya yang memiliki 512 bit, Anda harus melakukan lebih dari 500 perkalian, karena kita harus melakukan setidaknya 500 kotak dan beberapa lagi. Jadi Anda melakukan mod q dua kali dan kemudian mendapatkan banyak operasi divisi sederhana jika Anda tetap dalam bentuk angka yang mewakili ini. Dan pada akhirnya, Anda melakukan pembagian dengan R untuk kembali ke formulir ini ab.

Jadi, alih-alih melakukan mod q 500 kali untuk setiap langkah perkalian, Anda lakukan mod q dua kali dan kemudian terus melakukan pembagian ini dengan R dengan biaya minimal.
Hadirin: ketika Anda menambahkan beberapa q dan kemudian membaginya dengan R, apakah kita memiliki sisanya?
Profesor: sebenarnya mod q berarti sisanya ketika Anda membaginya dengan q. Sederhananya, x + yq mod q = x. Dalam hal ini, ada properti lain yang bermanfaat - bahwa semua modul adalah bilangan prima. Ini sama benarnya dengan fakta bahwa jika Anda memiliki (x + yq / R) mod q, maka itu sama dengan x / R mod q.



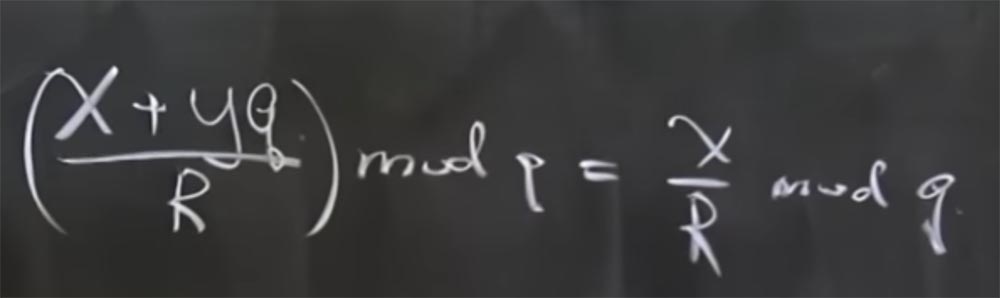
Alasan untuk berpikir demikian adalah karena tidak ada operasi pembagian nyata dalam aritmatika modular, itu hanya inversi. Bahkan, ini berarti bahwa jika kita memiliki (x + yq) dikalikan dengan R terbalik yang dihitung dengan mod q, maka itu sama dengan jumlah dua produk: produk x dari R terbalik dengan mod q dan produk yq oleh R terbalik dengan mod q. Selain itu, istilah terakhir dikurangi, karena itu adalah sesuatu yang dikalikan dengan q.



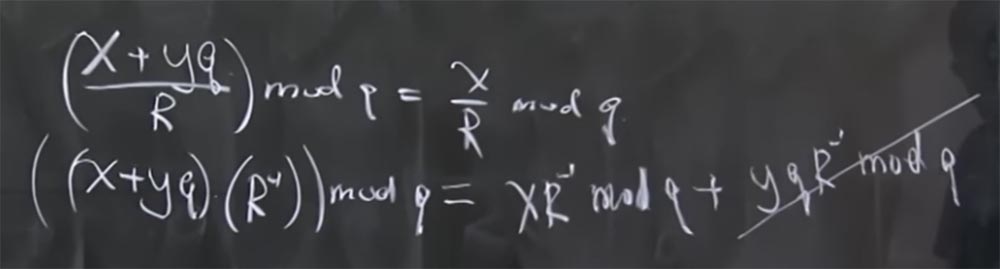
Untuk hal-hal seperti menjumlahkan 2q, 8q, dan seterusnya, ada rumus yang mempercepat proses perhitungan. Saya melakukannya secara bertahap, pertama dihitung 2q, lalu 8q dan seterusnya, tetapi materi kuliah memiliki formula lengkap yang dapat digunakan, saya hanya tidak ingin membuang waktu menulisnya di papan tulis. Ini memungkinkan Anda untuk menghitung berapa kelipatan dari nilai q yang harus Anda tambahkan sehingga semua bit paling signifikan berubah menjadi 0. Kemudian ternyata untuk melakukan pembagian dengan R, Anda hanya perlu menghitung kelipatan ajaib dari q ini, tambahkan, lalu buang yang rendah nol bit, dan ini akan mengembalikan nomor Anda menjadi 512 bit, berapa pun ukuran hasil yang Anda dapatkan.

Tapi ada satu kehalusan. Satu-satunya alasan kita berbicara tentang ini adalah karena sesuatu yang lucu sedang terjadi di sini, yang memungkinkan kita untuk mencari tahu informasi tentang timing. Secara khusus, meskipun kami dibagi dengan R, kami masih tahu bahwa hasilnya akan menjadi sekitar 512 bit. Tetapi masih bisa lebih dari q, karena q bukan angka 512-bit, itu bisa sedikit kurang dari R.

Jadi mungkin setelah kita membuat pembagian yang menguntungkan ini dengan R, kita mungkin perlu mengurangi q lagi, karena kita mendapatkan sesuatu yang kecil, tetapi masih belum cukup kecil. Jadi ada kemungkinan bahwa setelah pembagian ini kita mungkin harus mengurangi q lagi. Dan pengurangan ini dapat digunakan sebagai bagian dari serangan, karena operasi pengurangan menambah waktu perhitungan.



Dan seseorang menemukan - bukan orang-orang ini, tetapi seseorang dalam pekerjaan sebelumnya - bahwa ada kesempatan untuk melakukan sesuatu yang disebut pengurangan ekstra, atau pengurangan tambahan. , . , xd mod q, - x mod q, 2R. .



, x mod q , . , cd.



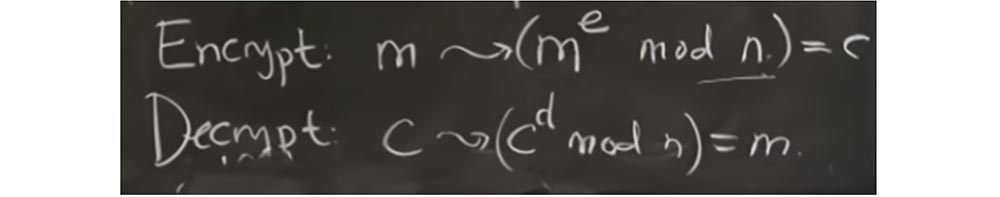
, extra reduction , X , , , q.



, c, extra reduction , c — q. , , q . , extra reduction, , , X mod q , = q + έ, . , . , , , , extra reduction .

: , ?

: , extra reduction? , , , . , . , , extra reduction, , , . , . , , mod q. , , , . , mod q , , .

, . , - , . — , . , - , extra reduction .

, . , OpenSSL, , . , mod q . , , .

, , , , a b. — 512- . , 32- , , 64- ? ?



- ? , , a b .

, , 512 , 64- , 32- . a : a ₁ a ₀ , a ₀ , a ₁ — . b – b ₁ b ₀ .

ab 3- : a ₁ b ₁ , a ₀ b ₀ , a ₁ b ₀ + a ₀ b ₁ . .



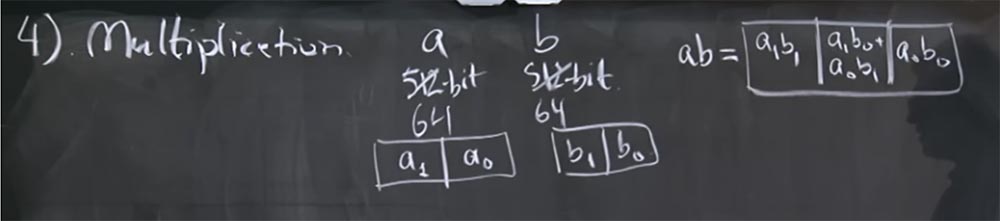
55:00

Kursus MIT "Keamanan Sistem Komputer". 16: « », 3


Versi lengkap dari kursus ini tersedia di sini .

Terima kasih telah tinggal bersama kami. Apakah Anda suka artikel kami? Ingin melihat materi yang lebih menarik? Dukung kami dengan melakukan pemesanan atau merekomendasikannya kepada teman-teman Anda, diskon 30% untuk pengguna Habr pada analog unik dari server entry-level yang kami temukan untuk Anda: Seluruh kebenaran tentang VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps dari $ 20 atau bagaimana membagi server? (opsi tersedia dengan RAID1 dan RAID10, hingga 24 core dan hingga 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps hingga Desember secara gratis ketika membayar untuk jangka waktu enam bulan, Anda dapat memesan di sini .

Dell R730xd 2 kali lebih murah? Hanya kami yang memiliki 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV dari $ 249 di Belanda dan Amerika Serikat! Baca tentang Cara Membangun Infrastruktur Bldg. kelas menggunakan server Dell R730xd E5-2650 v4 seharga 9.000 euro untuk satu sen?