Kursus MIT "Keamanan Sistem Komputer". Kuliah 16: “Serangan Saluran Samping”, Bagian 3

Institut Teknologi Massachusetts. Kursus Kuliah # 6.858. "Keamanan sistem komputer." Nikolai Zeldovich, James Mickens. Tahun 2014

Keamanan Sistem Komputer adalah kursus tentang pengembangan dan implementasi sistem komputer yang aman. Ceramah mencakup model ancaman, serangan yang membahayakan keamanan, dan teknik keamanan berdasarkan pada karya ilmiah baru-baru ini. Topik meliputi keamanan sistem operasi (OS), fitur, manajemen aliran informasi, keamanan bahasa, protokol jaringan, keamanan perangkat keras, dan keamanan aplikasi web.

Kuliah 1: “Pendahuluan: model ancaman” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 2: "Kontrol serangan hacker" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 3: “Buffer Overflows: Exploits and Protection” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 4: “Pemisahan Hak Istimewa” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 5: "Dari mana sistem keamanan berasal?" Bagian 1 / Bagian 2
Kuliah 6: “Peluang” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 7: “Kotak Pasir Klien Asli” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 8: “Model Keamanan Jaringan” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 9: "Keamanan Aplikasi Web" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 10: “Eksekusi simbolik” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 11: “Bahasa Pemrograman Web / Web” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 12: Keamanan Jaringan Bagian 1 / Bagian 2 / Bagian 3
Kuliah 13: "Protokol Jaringan" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 14: "SSL dan HTTPS" Bagian 1 / Bagian 2 / Bagian 3
Kuliah 15: “Perangkat Lunak Medis” Bagian 1 / Bagian 2 / Bagian 3
Kuliah 16: “Serangan Saluran Samping” Bagian 1 / Bagian 2 / Bagian 3

Hadirin: Apakah Anda menggunakan metode Karatsuba?

Profesor: ya, ini adalah metode perkalian pintar yang tidak memerlukan empat tahap perhitungan. Metode Karatsuba diajarkan dalam kursus 0,601, atau bagaimana itu ditunjuk hari ini?

Pemirsa: 042.

Profesor: 042, luar biasa. Ya, ini adalah metode yang sangat bagus. Hampir setiap perpustakaan kriptografi menggunakannya. Bagi Anda yang bukan lulusan lembaga kami - saya katakan ini karena kami memiliki mahasiswa pascasarjana di sini - saya akan menulis tentang metode Karatsuba di papan tulis. Di sini Anda perlu menghitung tiga nilai:

a ₁ b ₁
(a ₁ - a ₀ ) (b ₁ - b ₀ )
a ₀ b ₀

Dengan demikian, Anda melakukan 3 perkalian alih-alih empat, dan ternyata Anda dapat mengembalikan nilai ini ₁ b ₀ + a ₀ b ₁ dari tiga hasil penggandaan ini.



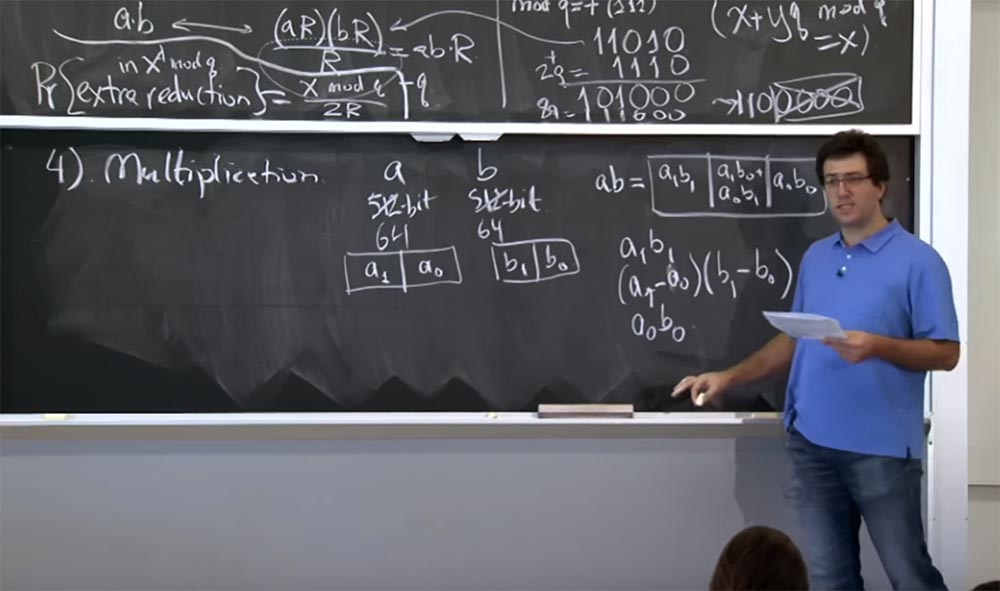
Cara khusus untuk melakukan ini adalah ini ... izinkan saya meletakkannya dalam bentuk yang berbeda.

Jadi, kita akan memiliki:

(2 ⁶⁴ + 2 ³² ) (a ₁ b ₁ ) +
(2 ³² ) (- (a ₁ - a ₀ ) (b ₁ - b ₀ )
(2 ³² + 1) (a ₀ b ₀ )

Ini tidak terlalu jelas, tetapi jika Anda mengerjakan perinciannya, maka pada akhirnya meyakinkan diri Anda bahwa nilai ini dalam 3 baris ini setara dengan ab, tetapi pada saat yang sama mengurangi perhitungan dengan satu penggandaan. Dan cara kami menerapkan ini pada penggandaan yang lebih banyak adalah bahwa Anda terus turun secara rekursif. Jadi, jika Anda memiliki nilai 512 bit, Anda dapat membaginya menjadi 256-bit multiplikasi. Anda melakukan tiga perkalian 256-bit, setiap kali secara rekursif menggunakan metode Karatsuba. Pada akhirnya, perhitungan Anda turun ke ukuran mesin dan dapat diproses dengan instruksi mesin tunggal.



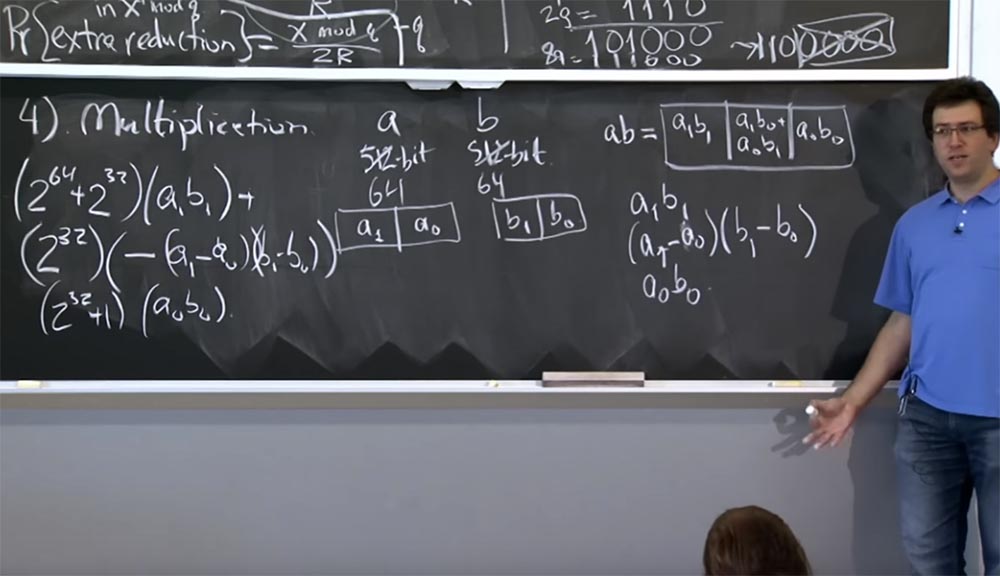
Jadi di mana serangan waktu? Bagaimana orang-orang ini menggunakan perkalian Karatsuba? Ternyata OpenSSL khawatir tentang dua jenis perkalian yang mungkin harus Anda lakukan.
Yang pertama adalah perkalian dua angka besar dengan ukuran yang kira-kira sama. Ini terjadi berkali-kali ketika kita melakukan eksponensial modular, karena semua nilai yang akan kita kalikan akan memiliki ukuran sekitar 512 bit. Oleh karena itu, ketika kita mengalikan c dengan y atau kuadrat, kita mengalikan dua hal dengan ukuran yang kira-kira sama. Dalam hal ini, metode Karatsuba sangat masuk akal, karena mengurangi jumlah angka yang dikuadratkan sekitar 1,58 kali, yang sangat mempercepat proses perhitungan.
Jenis perkalian kedua adalah ketika OpenSSL mengalikan dua angka yang ukurannya berbeda secara signifikan satu sama lain: satu sangat besar dan yang lain sangat kecil. Dalam hal ini, Anda juga bisa menggunakan metode Karatsuba, tetapi itu akan bekerja lebih lambat daripada perkalian primitif. Misalkan Anda mengalikan angka 512-bit dengan angka 64-bit, Anda harus menaikkan setiap bit dari angka pertama menjadi kekuatan 64, menghasilkan perlambatan proses 2n bukannya akselerasi n / 1.58. Oleh karena itu, orang-orang yang menggunakan OpenSSL mencoba melakukan lebih cerdas, dan di sinilah masalahnya dimulai.

Mereka memutuskan bahwa mereka akan secara dinamis beralih antara metode Karatsuba yang efektif dan metode multiplikasi sekolah dasar. Heuristik mereka adalah sebagai berikut. Jika dua angka yang Anda kalikan terdiri dari jumlah kata mesin yang sama, atau setidaknya memiliki jumlah bit yang sama dengan unit 32-bit, maka metode Karatsuba digunakan. Jika dua angka berbeda dalam ukuran satu sama lain, kuadrat atau langsung sederhana, perkalian normal dilakukan.

Dalam hal ini, Anda dapat melacak bagaimana peralihan ke metode perkalian lainnya terjadi. Karena saat peralihan tidak berlalu tanpa jejak, setelah itu akan terlihat apakah sekarang membutuhkan lebih banyak waktu untuk perkalian atau lebih sedikit dari sebelumnya. Para peneliti mengambil keuntungan dari keadaan ini untuk mengatur serangan menggunakan metode penentuan waktu.

Saya pikir saya telah selesai memberi tahu Anda tentang semua trik aneh yang digunakan orang ketika menerapkan RSA dalam praktik. Sekarang mari kita coba menyatukannya dan menggunakannya dalam kaitannya dengan seluruh server web untuk mengetahui bagaimana Anda dapat "mencubit" bit yang menarik bagi kami dari paket jaringan input.

Jika Anda ingat dari kuliah di HTTPS, server web memiliki kunci rahasia. Dia menggunakan kunci rahasia ini untuk membuktikan bahwa dia adalah pemilik yang benar dari semua sertifikat melalui HTTPS atau TLS. Ini disebabkan oleh fakta bahwa klien mengirim beberapa bit yang dipilih secara acak, bit-bit ini dienkripsi menggunakan kunci publik server, dan server mendekripsi pesan ini menggunakan protokol TLS. Dan jika pesan dicentang, maka bit acak ini digunakan untuk membangun sesi komunikasi.

Namun dalam kasus kami, pesan ini tidak akan diperiksa, karena akan dibuat dengan cara khusus, dan ketika ternyata bit tambahan tidak cocok, server akan mengembalikan kesalahan segera setelah selesai mendekripsi pesan kami.

Inilah yang akan kita lakukan di sini. Server - Anda dapat berasumsi bahwa itu adalah Apache dengan SSL terbuka - akan menerima pesan dari klien yang dianggap sebagai teks terenkripsi dengan atau beberapa teks terenkripsi hipotetis yang dibuat klien. Hal pertama yang kita lakukan dengan ciphertext c adalah mendekripsi menggunakan rumus dengan → (c ^d mod n) = m.

Jika Anda ingat optimasi pertama, kami akan menerapkan teorema sisa bahasa Mandarin dan membagi teks kami menjadi dua bagian: satu untuk menghitung dengan mod p, yang lain dengan mod q, dan kemudian menggabungkan hasilnya. Pertama, ambil c dan wakili dalam dua kuantitas: yang pertama disebut c ₀ , itu akan sama dengan mod q, dan yang kedua adalah c ₁ , dan itu akan sama dengan c mod p. Kemudian kita akan melakukan hal yang sama untuk menghitung c untuk d mod p dan c untuk d mod q.



Selanjutnya, kita akan beralih ke tampilan Montgomery karena ini akan membuat perkalian kita sangat cepat. Jadi hal berikutnya yang akan dilakukan SSL dengan nomor Anda adalah menghitung c ₀ ', yang akan sama dengan c ₀ R mod q dan melakukan hal yang sama di sini untuk c1, saya tidak akan menuliskannya karena terlihat sama .

Sekarang kita telah beralih ke bentuk Montgomery, kita akhirnya dapat melakukan penggandaan kita, dan di sini kita akan menggunakan teknik "sliding window". Segera setelah kita mendapatkan c ₀ ', kita membuat kenaikan sederhana ini c ₀ ' menjadi kekuatan d dalam mod q. Dan di sini, karena kita menghitung nilai ini untuk d, kita akan menggunakan "jendela geser" untuk bit eksponen d, dan kita juga akan menggunakan metode Karatsuba atau perkalian yang biasa, tergantung pada ukuran operan kita.



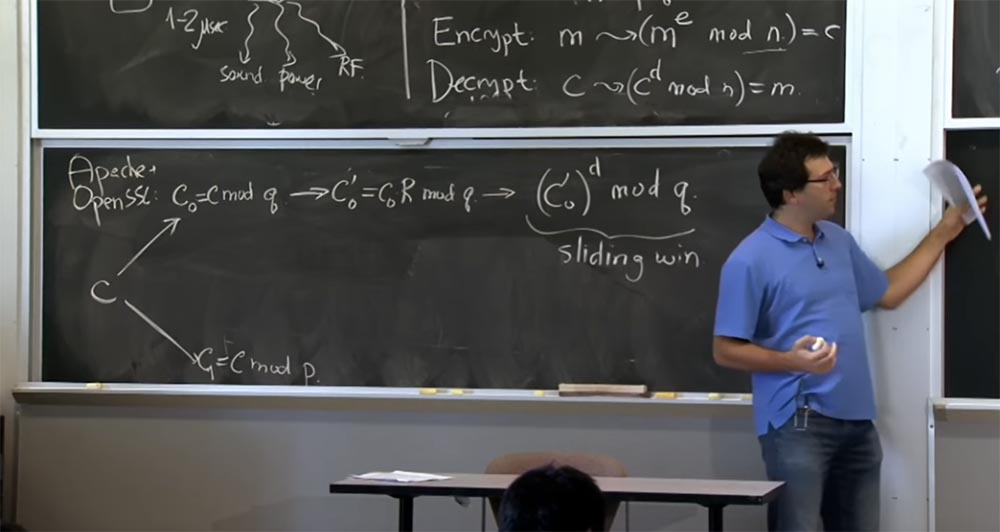
Jadi, jika ternyata nilai ini c ₀ 'dan hasil kuadrat yang diperoleh sebelumnya adalah ukuran yang sama, kami menggunakan metode Karatsuba. Jika c ₀ 'sangat kecil, dan hasil sebelumnya dari perkalian besar, maka kita akan kuadrat dan dikalikan dengan cara biasa. Di sini kita menggunakan "jendela geser" dan metode Karatsuba bukan perkalian normal.



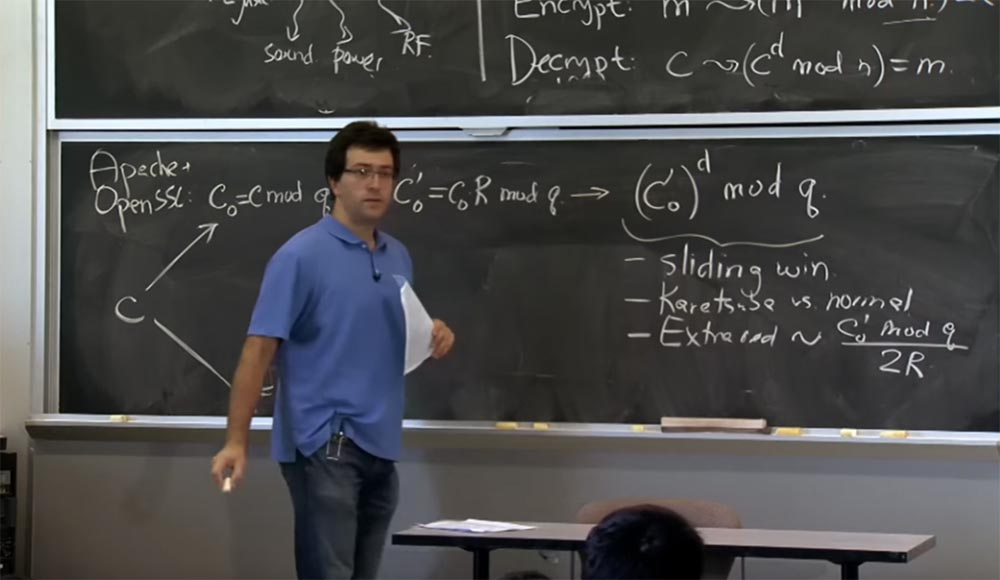
Juga pada tahap ini, pengurangan tambahan muncul. Karena dengan setiap perkalian, pengurangan tambahan akan sebanding dengan apa yang kita naikkan ke kekuatan dengan mod q, yaitu, dengan nilai (c ₀ ') ^d . Di sini, dengan koneksi rumus yang sederhana, kemungkinan pengurangan tambahan akan sebanding dengan nilai c ₀ 'mod q dibagi dengan 2R. Di tempat inilah sedikit muncul yang mempengaruhi waktu.

Faktanya, ada dua kemungkinan efek: menggunakan metode Karatsuba alih-alih perkalian normal dan penampilan singkatan tambahan yang akan Anda lakukan.

Dalam sedetik Anda akan melihat bagaimana itu dapat digunakan. Sekarang, ketika Anda mendapatkan hasil ini untuk mod q dan akan mendapatkan hasil yang serupa untuk mod p, Anda akhirnya dapat menggabungkan kembali kedua bagian ini di bagian atas dan bawah dan menggunakan CRT, teorema sisa Cina.

Dan apa yang Anda dapatkan dari CRT sebagai hasilnya ... maaf, saya pikir kita perlu mengonversi ini kembali dari formulir Montgomery terlebih dahulu. Oleh karena itu, sebelum rekombinasi, kami mengonversi bagian atas ke ekspresi (c ₀ ') ^d / R mod q dan mengembalikan nilai kami cd mod q. Di bagian bawah, kami memperoleh cd mod p.

Sekarang Anda dapat menggunakan CRT untuk mendapatkan nilai c ^d mod n. Maaf untuk font kecil, saya tidak punya cukup papan tulis. Tentang hal yang sama kita dapatkan di sini di bawah ini dengan ₁ , dan kita akhirnya bisa mendapatkan hasil kita, yaitu pesan m.



Jadi, server mengambil paket masuk yang diterimanya, menjalankannya melalui seluruh pipa ini, mengeksekusi dua bagian dari pipa ini, dan berakhir dengan pesan yang didekripsi m sama dengan cd mod m. Lalu dia akan memeriksa padding padding dari postingan ini. Dalam kasus serangan khusus kami, kami membuat sedemikian rupa sehingga penambahan ini tidak akan cocok. Kami memilih nilai c untuk heuristik yang tidak mengenkripsi pesan nyata dengan penambahan padding yang benar.

Dengan demikian, add-on tidak lulus tes, server harus mencatat kesalahan, mengirim pesan kesalahan ke klien dan memutuskan sambungan. Jadi, kami akan mengukur waktu yang diperlukan server untuk menyampaikan pesan kami melalui pipa ini. Apakah Anda memiliki pertanyaan tentang proses memproses pesan oleh server dan menggabungkan semua optimasi ini?

Pemirsa: menurut saya, ada kesalahan dengan indeks besarnya c.

Profesor: ya, Anda benar, saya menambahkan indeks 0, di sini harus c ₀ ^d mod q.



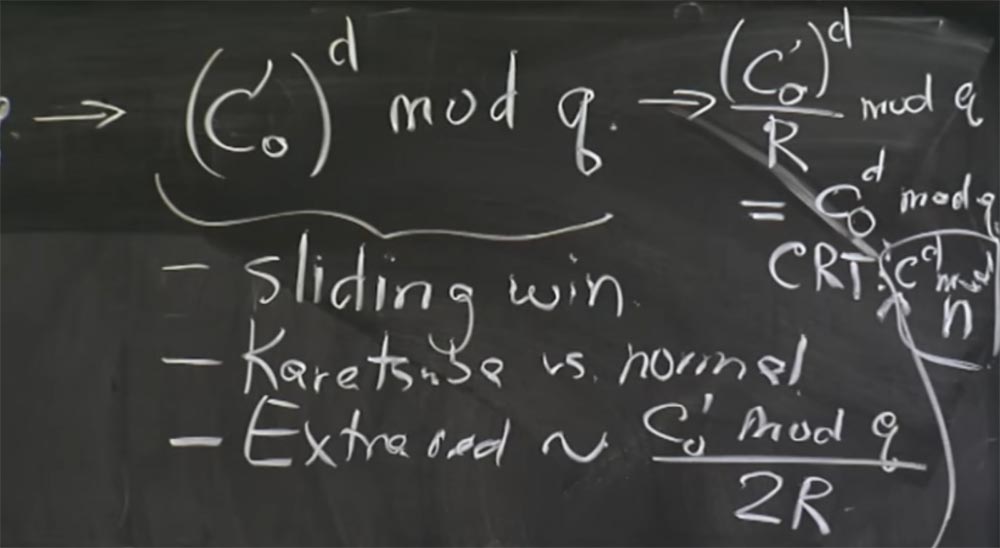Hadirin: ketika Anda membaginya dengan R mod q, apakah tidak ada asumsi tentang berapa q yang harus Anda tambahkan untuk semakin mengurangi bit rendah menjadi nol?

Profesor: ya, Anda benar, pada tahap akhir ini (c ₀ ') ^d / R mod q mungkin ada pengurangan tambahan. Jadi kita harus melakukan pembagian ini dengan R dengan cara yang benar, dan mungkin harus melakukan hal yang sama dengan melakukan pengurangan Montgomery di sini, ketika kita membaginya dengan R, untuk mengubah nilai kembali. Karena pada awal perhitungan tidak jelas persis berapa banyak q yang harus kita tambahkan, kita menggunakan metode seleksi, hancurkan nol yang rendah, lalu buat lagi mod q, dan, mungkin, pengurangan tambahan. Anda benar-benar benar, dalam hal ini pembagian yang sama persis dengan R mod q untuk setiap langkah multiplikasi Montgomery.

Jadi, bagaimana Anda memanfaatkan ini? Bagaimana penyerang bisa memecahkan kunci rahasia server dengan mengukur waktu yang dibutuhkan untuk menyelesaikan operasi? Orang-orang ini memiliki rencana yang didasarkan pada menebak sedikit kunci pribadi pada suatu waktu. Kita dapat mengasumsikan bahwa kunci rahasia adalah eksponen terenkripsi d, karena Anda tahu dan tahu, ini adalah kunci publik. Satu-satunya hal yang tidak Anda ketahui adalah d.



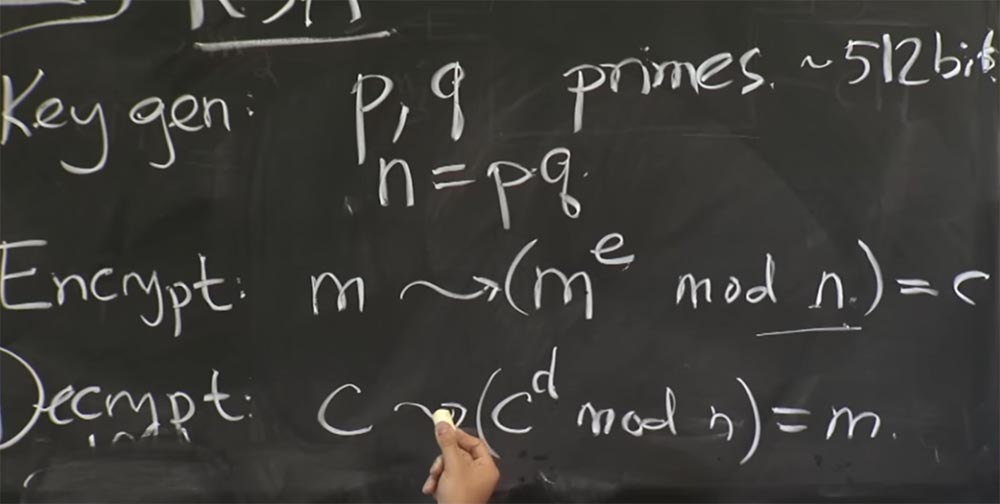
Bahkan, dalam serangan ini, mereka tidak langsung menebak nilai d, karena agak rumit. Sebaliknya, mereka mempertimbangkan q atau p, tidak peduli yang mana dari dua kuantitas ini. Setelah Anda menebak apa yang penting, Anda dapat menghitung n = pq. Kemudian, jika Anda mengetahui nilai-nilai p dan q, Anda dapat menghitung fungsi φ yang telah kita bicarakan sebelumnya. Ini akan memungkinkan Anda untuk mendapatkan nilai d dari nilai e. Jadi, faktorisasi nilai n ini sangat penting, harus dirahasiakan untuk memastikan keamanan RSA.

Jadi sebenarnya, orang-orang ini bermaksud menebak nilai q dengan menganalisis timing pipa ini. Apa yang mereka lakukan untuk ini? Mereka dengan hati-hati memilih nilai awal dari nilai c dan mengukur waktu perjalanannya melalui pipa server.

Secara khusus, ada dua bagian untuk serangan ini, dan Anda harus mengambil beberapa langkah awal untuk menebak beberapa bit pertama. Kemudian, segera setelah Anda memiliki beberapa bit pertama, Anda dapat menebak bit berikutnya. Oleh karena itu, saya tidak memberi tahu Anda secara rinci bagaimana mereka menebak beberapa bit pertama, karena pada kenyataannya jauh lebih menarik untuk mempertimbangkan bagaimana mereka menebak bit berikutnya. Jika kita punya waktu, kita akan kembali ke bagaimana menebak beberapa bit awal dijelaskan dalam artikel kuliah.

Jadi, anggaplah Anda memiliki asumsi g tentang bit apa yang ada dalam nilai q ini. Biarkan nilai ini terdiri dari bit-bit seperti: g = g ₀ g ₁ g ₂ ... dan seterusnya. Sebaliknya, ini bahkan bukan g, tetapi bit q yang asli, jadi izinkan saya menulis ulang seperti ini: g = q ₀ q ₁ q ₂ .... Kami percaya bahwa q ini adalah bit tinggi, dan kami mencoba menebak bit lebih rendah dan lebih rendah. Misalkan kita tahu nilai q hingga bit qj, dan kemudian semua nol mengikuti. Anda tidak tahu apa sisa bitnya.



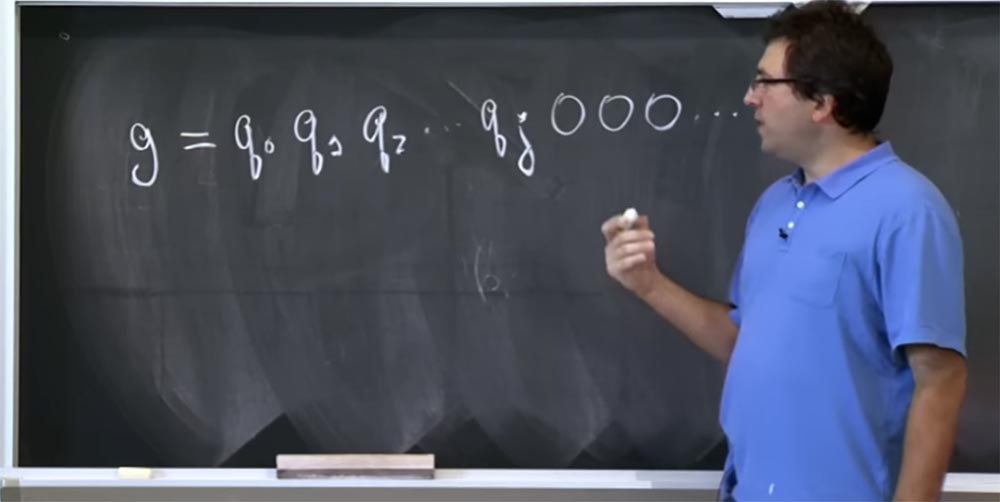
Orang-orang ini mencoba menyuntikkan dugaan ini ke tempat pipa kami ini: (c0 ') d mod q. Karena ini adalah tempat di mana dua jenis optimasi digunakan: metode Karatsub bukan perkalian biasa dan jumlah singkatan tambahan yang berbeda tergantung pada nilai c ₀ '. Sebenarnya, mereka mencoba untuk memperkenalkan dua tebakan berbeda ke tempat pipa ini: yang pertama, yang terlihat seperti g = q ₀ q ₁ q ₂ ... qj 000 ... 0000, dan yang kedua, yang mereka sebut g _tinggi , yang terdiri dari bit tinggi yang sama, tetapi sebaliknya dari semua nol di akhir ada unit yang menunjukkan bit tinggi, diikuti oleh nol lagi:

g = q ₀ q ₁ q ₂ ... qj 100 ... 0000.

Bagaimana ini membantu orang-orang ini memahami apa yang terjadi? Ada dua cara untuk melakukan ini. Misalkan tebakan kita g sama dengan nilai c ₀ '. Kita dapat mengasumsikan bahwa g dan g ini sesuai dengan nilai c ₀ 'yang diberikan pada papan kiri. Sebenarnya, ini cukup sederhana untuk melakukan ini, karena c ₀ 'cukup mudah untuk menghitung mundur dari nilai input terenkripsi c ₀ , Anda hanya mengalikannya dengan R.



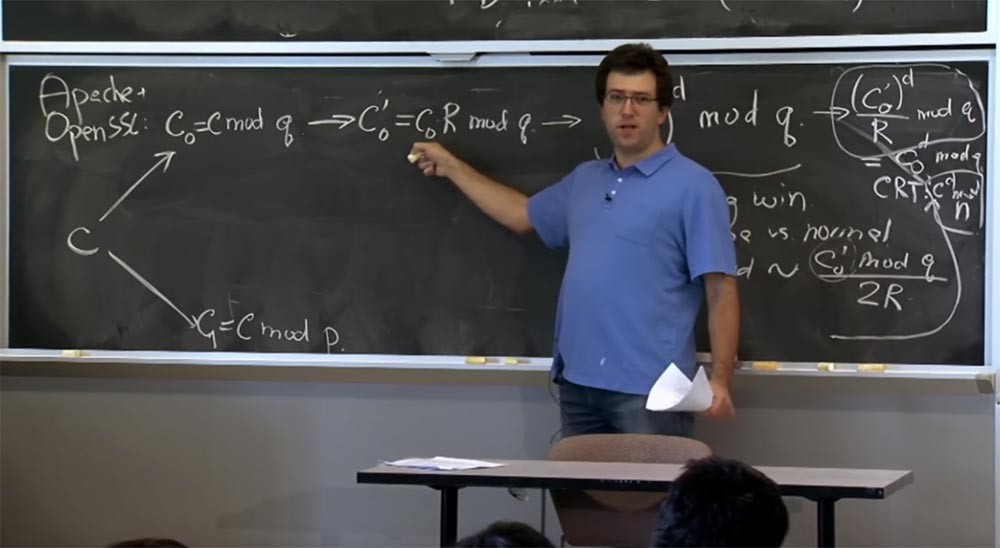
Oleh karena itu, untuk menebak nilai (c ₀ ') ^d , mereka hanya perlu mengambil tebakan mereka, tebakan mereka g, dan pertama-tama membaginya dengan R, yaitu, membagi dengan 512 mod sesuatu di sana. Kemudian mereka akan memperkenalkannya kembali, server akan mengalikannya dengan R dan melanjutkan proses yang dijelaskan dalam skema pipa kami.

Jadi, anggaplah kita mampu menempatkan nilai integer tertentu yang dipilih di tempat yang tepat. Jadi, apa yang akan menjadi waktu perhitungan c ₀ 'to d mod q?



Ada dua opsi yang memungkinkan di mana q cocok dengan gambar ini. Bisa jadi q berada di antara dua nilai g dan g _{tinggi ini} , karena bit q berikutnya adalah 0. Dengan demikian, nilai ini - 0 pertama setelah qj - akan lebih kecil dari q, tetapi nilai ini - 1 setelah q - akan lebih dari q. Ini terjadi jika bit q berikutnya adalah 0, atau ada kemungkinan q berada di atas kedua nilai ini jika bit q berikutnya adalah 1.



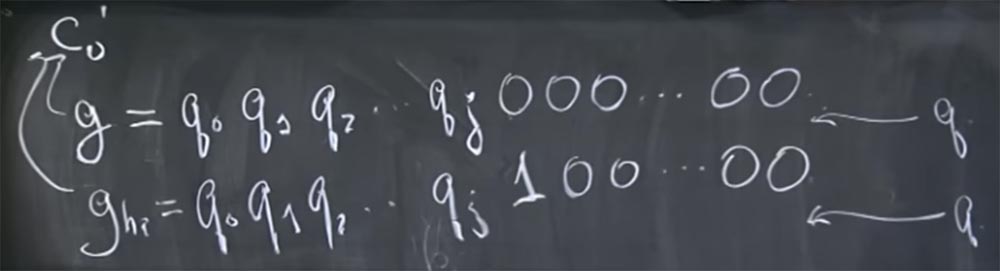
Sekarang kita dapat mengatakan berapa waktu dekripsi dari kedua nilai ini jika q terletak di antara keduanya, atau jika q terletak di atas keduanya.

Mari kita lihat situasi di mana q berada di atas. Dalam hal ini, semuanya hampir sama. Karena kedua nilai ini kurang dari q, nilai hal-hal ini dalam mod q akan kira-kira sama. Mereka sedikit berbeda karena bit ekstra ini, tetapi ukurannya masih kurang lebih sama. Dan jumlah reduksi tambahan, reduksi ekstra, juga mungkin tidak akan banyak berbeda, karena sebanding dengan nilai c0 'mod q. Dan untuk nilai g dan g _tinggi kurang dari q, semuanya hampir sama. Tak satu pun dari mereka akan melebihi q dan tidak akan menyebabkan sejumlah besar pengurangan tambahan, karena untuk q lebih besar dari kedua tebakan ini, jumlah perhitungan dengan metode Karatsuba sehubungan dengan jumlah perhitungan biasa akan tetap sama. Dalam hal hubungan ini, server akan menangani g dan g sama _tinggi . Oleh karena itu, server akan membuat singkatan tambahan yang sama untuk kedua nilai ini. Jadi, jika Anda melihat bahwa server menghabiskan waktu yang sama menanggapi dugaan ini, maka Anda mungkin harus berasumsi bahwa benar-benar ada 1 dalam nilai g _tinggi pada saat ini.



Di sisi lain, jika q terletak di antara kedua nilai ini, maka ada dua kemungkinan hal yang dapat menyebabkan perubahan dan pengaturan waktu. Salah satu hal adalah bahwa karena g _tinggi sedikit lebih besar dari q, jumlah potongan tambahan akan sebanding dengan c 'mod q, yang sangat kecil karena c ₀ ' adalah q ditambah beberapa bit dalam urutan bit ekstra ini dari 100 ... 00 Dengan demikian, jumlah pengurangan tambahan akan lebih terlihat dan semuanya akan mulai terjadi lebih cepat.
, , , , , : «, !». , g c ₀ ' , q, , g _high q, g _high mod q . , . – , , .

c ₀ ' mod q. c ₀ g _high , q, , g q. , . , , . , 32- , .

, 32- , , , . , . 32 , , - . , , 32, , , , .

, , , . , q 1, , q 0, , g _high q , , .

. , . , . , , 1-2 . , , Ethernet.
, . . , 7 . , , -, , ?

: ?

: , , , , , . , .

, , 7 , , 7 . 7 g, 7 g + 1, g + 2 7 g + 400. g, g, , 7 400, ?



: , , ?

: , , , — (c ₀ ') ^d . . , , , mod p. , , . , g, 1, 2, 3, , .

, , – 100…00. , mod p, , mod p . « », , (c ₀ ') ^d , . ?

: , ?

: - , q. , q, , , .

: c ₀ '?

: c ₀ ', c, c ₀ ' R mod n.



, «» , c ₀ = mod q, c ₀ = ((c ₀ ' R ^-1 ) mod n) mod q. R, R. c ₀ ', (c ₀ ') ^d mod q. , , , , R. , R = 2 ⁵¹² . , .

: mod p ?

:yaitu, Anda tidak tahu apa itu, tetapi Anda ingin mendefinisikannya secara acak? Jika Anda berhasil, maka Anda akan melakukan pekerjaan dengan baik! Nah, minggu depan kita akan mulai membahas masalah lain.


Versi lengkap dari kursus ini tersedia di sini .

Terima kasih telah tinggal bersama kami. Apakah Anda suka artikel kami? Ingin melihat materi yang lebih menarik? Dukung kami dengan melakukan pemesanan atau merekomendasikannya kepada teman-teman Anda, diskon 30% untuk pengguna Habr pada analog unik dari server entry-level yang kami temukan untuk Anda: Seluruh kebenaran tentang VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps dari $ 20 atau bagaimana membagi server? (opsi tersedia dengan RAID1 dan RAID10, hingga 24 core dan hingga 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps hingga Desember secara gratis ketika membayar untuk jangka waktu enam bulan, Anda dapat memesan di sini .

Dell R730xd 2 kali lebih murah? Hanya kami yang memiliki 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV dari $ 249 di Belanda dan Amerika Serikat! Baca tentang Cara Membangun Infrastruktur Bldg. kelas menggunakan server Dell R730xd E5-2650 v4 seharga 9.000 euro untuk satu sen?