🙌🏽 🐎 🍢 Julia dan gerakan partikel bermuatan dalam medan elektromagnetik 🖖🏻 🛀🏾 🤴🏻

Kami memperkuat keterampilan memecahkan dan memvisualisasikan persamaan diferensial menggunakan salah satu persamaan evolusi paling umum sebagai contoh, mengingat Scilab tua yang baik dan mencoba untuk memahami jika kita membutuhkannya ... Di bawah gambar yang dipotong (kilobyte untuk tujuh ratus)

Pastikan perangkat lunak baru

julia>] (v1.0) pkg>update #   (v1.0) pkg> status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.14.1+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Mari kita membaca panduan masa lalu

dan lanjutkan ke pernyataan masalah

Pergerakan partikel bermuatan dalam medan elektromagnetik

Pada partikel bermuatan dengan muatan $q$ bergerak dalam EMF dengan kecepatan $u$ pasukan Lorentz bertindak: $\ vec {F} _L = q \ kiri (\ vec {E} + \ kiri [\ vec {u} \ kali \ vec {B} \ kanan] \ kanan)$ . Formula ini valid dengan sejumlah penyederhanaan. Mengabaikan koreksi pada teori relativitas, kami menganggap massa partikel konstan, sehingga persamaan gerak memiliki bentuk: $\ frac {d} {dt} (m \ vec {u}) = q \ kiri (\ vec {E} + \ kiri [\ vec {u} \ kali \ vec {B} \ kanan] \ kanan)$

Mari kita mengarahkan sumbu Y sepanjang medan listrik, sumbu Z sepanjang medan magnet, dan mengasumsikan untuk kesederhanaan bahwa kecepatan partikel awal terletak di bidang XY. Dalam hal ini, seluruh lintasan partikel juga akan terletak di bidang ini. Persamaan gerak akan berbentuk:

\ left \ {\ begin {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ kanan.

$\ left \ {\ begin {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ kanan.$

Tak Terukur: $x ^ * = \ frac {x} {\ lambda}, \, y ^ * = \ frac {y} {\ lambda}, \, \ tau = \ frac {ct} {\ lambda}, \, B ^ * = \ frac {Bmc} {q \ lambda}, \, E ^ * = \ frac {Emc ^ 2} {q \ lambda}$ . Tanda bintang menunjukkan jumlah dimensi, dan $\ lambda$ - ukuran karakteristik sistem fisik yang dipertimbangkan. Kami memperoleh sistem persamaan gerak tak berdimensi dari partikel bermuatan dalam medan magnet:

\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ benar.

$\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ benar.$

Mari kita turunkan urutannya:

\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \ benar.

$\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \ benar.$

Sebagai konfigurasi awal model, kami memilih: $B = 2$ T $E = 5 \ cdot 10 ^ 4$ V / m $v_0 = 7 \ cdot 10 ^ 4$ m / s Untuk solusi numerik, kami menggunakan paket DifferentialEquations :

Kode dan Grafik

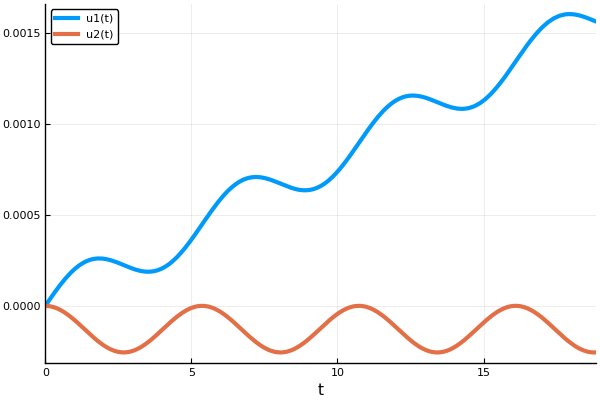
 using DifferentialEquations, Plots pyplot() M = 9.11e-31 # kg q = 1.6e-19 # C C = 3e8 # m/s λ = 1e-3 # m function modelsolver(Bo = 2., Eo = 5e4, vel = 7e4) B = Bo*q*λ / (M*C) E = Eo*q*λ / (M*C*C) vel /= C A = [0. 0. 1. 0.; 0. 0. 0. 1.; 0. 0. 0. B; 0. 0. -B 0.] syst(u,p,t) = A * u + [0.; 0.; 0.; E] # ODE system u0 = [0.0; 0.0; vel; 0.0] # start cond-ns tspan = (0.0, 6pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, Euler(), dt = 1e-4, save_idxs = [1, 2], timeseries_steps = 1000) end Solut = modelsolver() plot(Solut)

Di sini kita menggunakan metode Euler, yang jumlah langkahnya ditentukan. Juga, bukan seluruh solusi sistem disimpan dalam matriks jawaban, tetapi hanya 1 dan 2 indeks, yaitu, koordinat X dan pemain (kita tidak perlu kecepatan).

 X = [Solut.u[i][1] for i in eachindex(Solut.u)] Y = [Solut.u[i][2] for i in eachindex(Solut.u)] plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1)) title!(" ") yaxis!("Y") savefig("XY1.png")#

Periksa hasilnya. Kami memperkenalkan variabel baru, bukan x $\ tilde {x} = x-ut$ . Dengan demikian, transisi dibuat untuk sistem koordinat baru yang bergerak relatif terhadap yang asli dengan kecepatan u ke arah sumbu X :

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matrix} \ benar.

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matrix} \ benar.$

Jika Anda memilih $u = E / B$ dan menunjukkan $\ omega = qB / m$ , maka sistem akan disederhanakan:

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { matrix} \ benar.

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { matrix} \ benar.$

Medan listrik telah menghilang dari persamaan terakhir, dan mereka adalah persamaan gerak partikel di bawah pengaruh medan magnet yang seragam. Dengan demikian, partikel dalam sistem koordinat baru (x, y) harus bergerak dalam lingkaran. Karena sistem koordinat baru ini sendiri bergerak relatif terhadap yang asli dengan kecepatan $u = E / B$ , maka gerak partikel yang dihasilkan akan terdiri dari gerakan seragam sepanjang sumbu X dan rotasi di sekitar lingkaran pada bidang XY . Seperti yang Anda ketahui, lintasan yang terjadi ketika kedua gerakan ini ditambahkan bersama umumnya adalah trochoid . Khususnya, jika kecepatan awal adalah nol, kasus gerak paling sederhana dari jenis ini direalisasikan - sepanjang sikloid .
Mari kita pastikan bahwa kecepatan drift benar-benar sama dengan E / V. Untuk melakukan ini:

kami akan merusak matriks respons dengan menetapkan nilai yang sengaja lebih rendah daripada elemen pertama (maksimum)
kami menemukan jumlah elemen maksimum di kolom kedua dari matriks respons, yang ditunda oleh ordinat
kami menghitung kecepatan drift tanpa dimensi dengan membagi nilai absis maksimum dengan nilai waktu yang sesuai

 Y[1] = -0.1 numax = argmax( Y ) X[numax] / Solut.t[numax]

Keluar: 8.334546850446588e-5

 B = 2*q*λ / (M*C) E = 5e4*q*λ / (M*C*C) E/B

Keluar: 8.33333333333333332e-5
Hingga urutan ketujuh!
Untuk kenyamanan, kami mendefinisikan fungsi yang mengambil parameter model dan tanda tangan grafik, yang juga akan berfungsi sebagai nama file png yang dibuat dalam folder proyek (berfungsi dalam Juno / Atom dan Jupyter). Tidak seperti Gadfly , di mana grafik dibuat berlapis - lapis dan kemudian ditampilkan oleh fungsi plot () , di Plot, untuk membuat grafik yang berbeda dalam satu bingkai, yang pertama dibuat oleh fungsi plot () , dan yang berikutnya ditambahkan menggunakan plot! () . Nama-nama fungsi yang mengubah objek yang diterima di Julia biasanya berakhir dengan tanda seru.

 function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4) Ans = modelsolver(Bo, Eo, vel) X = [Ans.u[i][1] for i in eachindex(Ans.u)] Y = [Ans.u[i][2] for i in eachindex(Ans.u)] plot!(X, Y) p = title!(ttle) savefig( p, ttle * ".png" ) end

Pada nol kecepatan awal, seperti yang diharapkan, kami memperoleh cycloid :

 plot() plotter("Zero start velocity", 2, 4e4, 7e4)

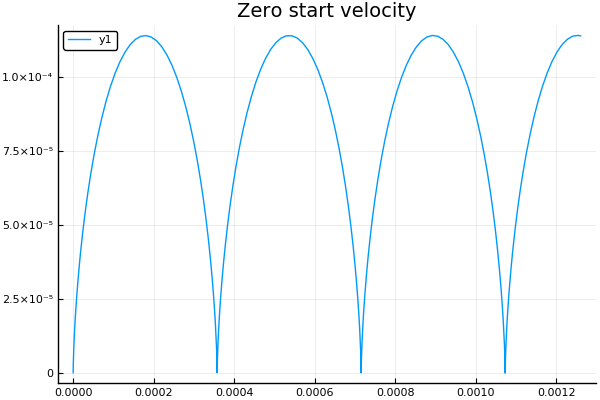
Kami mendapatkan lintasan partikel ketika induksi, intensitas, dan ketika tanda muatan berubah. Biarkan saya mengingatkan Anda bahwa titik berarti eksekusi berurutan fungsi dengan semua elemen array

Terselip

 plot() plotter.("B   ", 0, [3e4 4e4 5e4 6e4] )

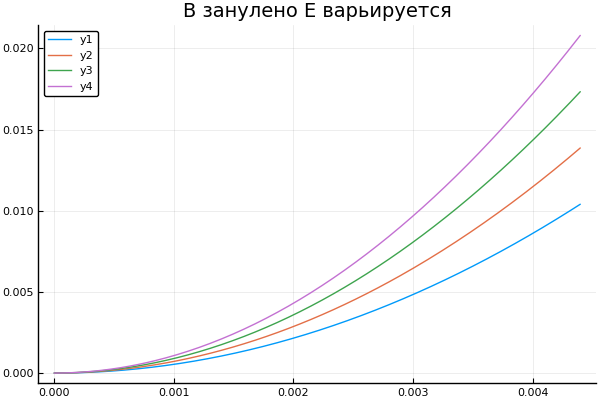
 plot() plotter.("E  B ", [1 2 3 4], 0 )

 q = -1.6e-19 # C plot() plotter.(" ")

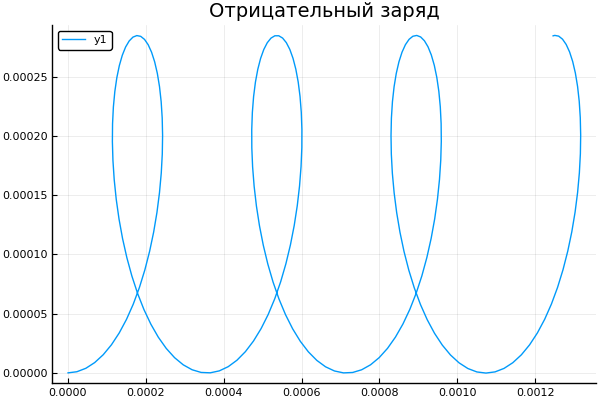
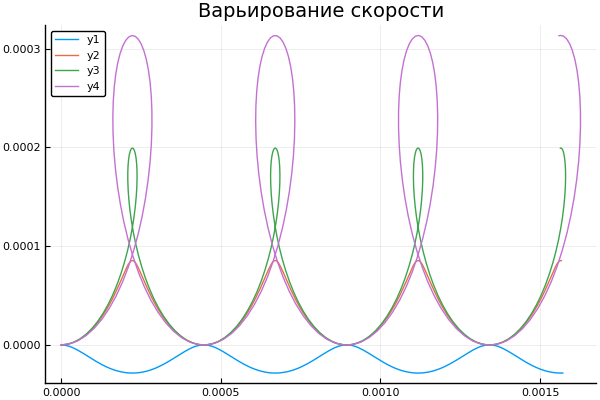
Dan mari kita lihat bagaimana perubahan kecepatan awal memengaruhi lintasan partikel:

 plot() plotter.(" ", 2, 5e4, [2e4 4e4 6e4 8e4] )

Sedikit tentang Scilab

Di Habré sudah ada informasi yang cukup tentang Silab, misalnya 1 , 2 , dan di sini tentang Oktaf karena itu kami akan membatasi diri untuk tautan ke Wikipedia dan ke beranda .

Sendiri, saya akan menambahkan tentang kehadiran antarmuka yang nyaman dengan kotak centang, tombol dan grafik, dan alat pemodelan visual Xcos yang agak menarik. Yang terakhir dapat digunakan, misalnya, untuk mensimulasikan sinyal dalam teknik listrik:

Spoiler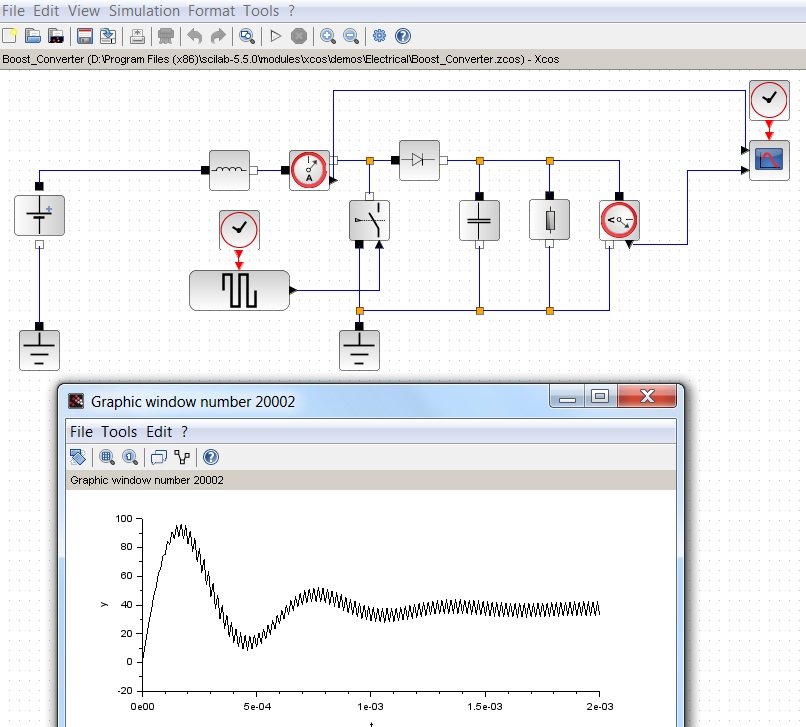

Dan ini adalah panduan yang sangat mudah:

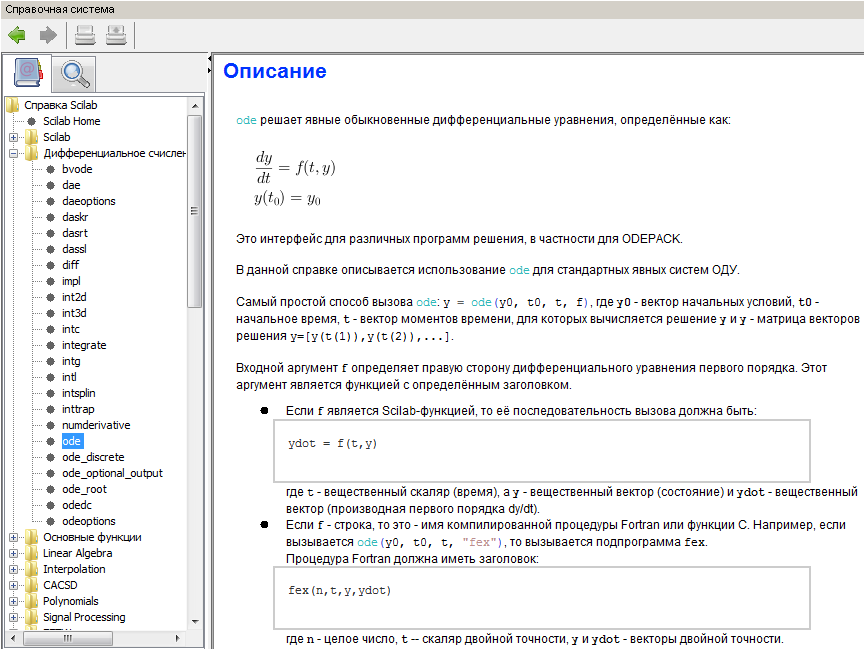
Sebenarnya, tugas kita juga bisa diselesaikan di Scilab:

Kode dan gambar

 clear function du = syst(t, u, A, E) du = A * u + [0; 0; 0; E] // ODE system endfunction function [tspan, U] = modelsolver(Bo, Eo, vel) B = Bo*q*lambda / (M*C) E = Eo*q*lambda / (M*C*C) vel = vel / C u0 = [0; 0; vel; 0] // start cond-ns t0 = 0.0 tspan = t0:0.1:6*%pi // time period A = [0 0 1 0; 0 0 0 1; 0 0 0 B; 0 0 -B 0] U = ode("rk", u0, t0, tspan, list(syst, A, E) ) endfunction M = 9.11e-31 // kg q = 1.6e-19 // C C = 3e8 // m/s lambda = 1e-3 // m [cron, Ans1] = modelsolver( 2, 5e4, 7e4 ) plot(cron, Ans1 ) xtitle ("   ","t","x, y, dx/dt, dy/dt"); legend ("x", "y", "Ux", "Uy"); scf(1)//    plot(Ans1(1, :), Ans1(2, :) ) xtitle (" ","x","y"); xs2png(0,'graf1');//       xs2jpg(1,'graf2');// ,  -

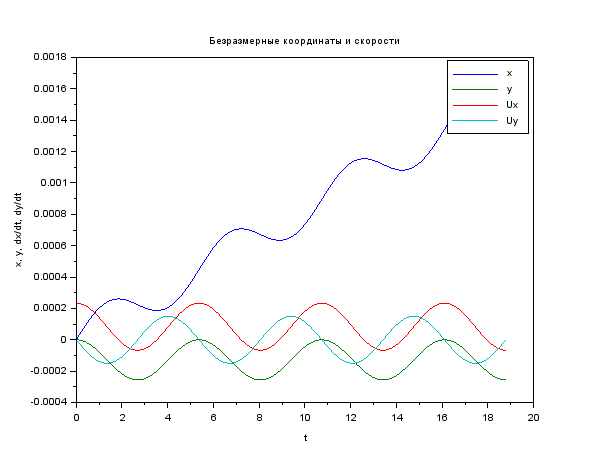
Berikut adalah informasi tentang fungsi untuk memecahkan ode diffurs . Pada prinsipnya, pertanyaan itu muncul

Mengapa kita membutuhkan Julia?

... jika ada hal-hal indah seperti Scilab, Oktaf dan Numpy, Scipy?
Tentang dua yang terakhir saya tidak akan mengatakan - Saya belum mencobanya. Dan secara umum pertanyaannya rumit, jadi mari kita lihat:

Scilab
Pada hard drive akan membutuhkan sedikit lebih dari 500 MB, itu dimulai dengan cepat dan segera ada perhitungan diferensial yang tersedia, grafik, dan yang lainnya. Baik untuk pemula: panduan yang sangat baik (sebagian besar diterjemahkan), ada banyak buku dalam bahasa Rusia. Tentang kesalahan internal telah dikatakan di sini dan di sini , dan karena produk sangat ceruk, komunitasnya lamban, dan modul tambahan sangat langka.

Julia
Ketika paket ditambahkan (terutama sembarang python-a la Jupyter dan Mathplotlib), paket ini tumbuh dari 376 MB menjadi sedikit lebih dari enam gigabytes. Ia juga tidak menggunakan RAM: pada awal 132 MB dan setelah merencanakan jadwal di Jupiter, ia akan dengan tenang mencapai 1 GB. Jika Anda bekerja di Juno , maka semuanya hampir seperti di Scilab : Anda dapat langsung mengeksekusi kode dalam interpreter, Anda dapat mencetak di notepad bawaan dan menyimpannya sebagai file, ada browser variabel, log perintah, dan bantuan online. Secara pribadi, saya marah pada kurangnya clear () , yaitu, saya menjalankan kode, kemudian mulai memperbaiki dan mengganti nama, dan variabel lama tetap (tidak ada browser variabel di Jupiter).

Tetapi semua ini tidak kritis. Scilab sangat cocok untuk pasangan pertama, membuat dahi, kursor, atau menghitung sesuatu di antaranya adalah alat yang sangat improvisasi. Meskipun ada juga dukungan untuk komputasi paralel dan memanggil fungsi sishn / Fortran, yang tidak dapat digunakan secara serius. Array besar membuatnya takut, untuk mengatur multidimensi, Anda harus berurusan dengan semua jenis obskurantisme , dan perhitungan di luar ruang lingkup tugas-tugas klasik dapat membuat semuanya hilang bersamaan dengan OS.

Dan setelah semua rasa sakit dan kekecewaan ini, Anda dapat dengan aman beralih ke Julia untuk mendapatkan di sini juga. Kami akan terus belajar, manfaat dari komunitas sangat responsif, masalah diselesaikan dengan cepat, dan Julia memiliki banyak fitur menarik yang akan mengubah proses pembelajaran menjadi perjalanan yang mengasyikkan!

Julia dan gerakan partikel bermuatan dalam medan elektromagnetik

Pergerakan partikel bermuatan dalam medan elektromagnetik

Sedikit tentang Scilab

Mengapa kita membutuhkan Julia?

More articles: