• Program pendidikan tentang teori probabilitas (artikel pengantar, opsional)
  
• Pengantar sistem persamaan linear
  
• Metode elemen hingga
  
• Minimalisasi bentuk kuadratik dan contoh masalah OLS
  
• Dari Kotak Terkecil ke Jaringan Saraf Tiruan
  

Jadi, artikel lain dari siklus "matematika di jari ". Hari ini kami melanjutkan diskusi tentang metode kuadrat terkecil, tetapi kali ini dari sudut pandang programmer. Ini adalah artikel lain dalam seri ini, tetapi terpisah, karena umumnya tidak memerlukan pengetahuan matematika. Artikel itu disusun sebagai pengantar teori, jadi dari keterampilan dasar itu membutuhkan kemampuan untuk menyalakan komputer dan menulis lima baris kode. Tentu saja, saya tidak akan membahas artikel ini, dan dalam waktu dekat saya akan menerbitkan sekuelnya. Jika saya dapat menemukan waktu yang cukup, maka saya akan menulis buku dari bahan ini. Target audiens adalah programmer, jadi Habr adalah tempat yang tepat untuk masuk. Secara umum, saya tidak suka menulis formula, dan saya sangat suka belajar dari contoh, bagi saya itu sangat penting - tidak hanya untuk melihat coretan di papan sekolah, tetapi untuk mencoba semua yang ada di gigi.

Jadi mari kita mulai. Mari kita bayangkan bahwa saya memiliki permukaan triangulasi dengan pemindaian wajah saya (pada gambar di sebelah kiri). Apa yang harus saya lakukan untuk meningkatkan fitur, mengubah permukaan ini menjadi topeng aneh?



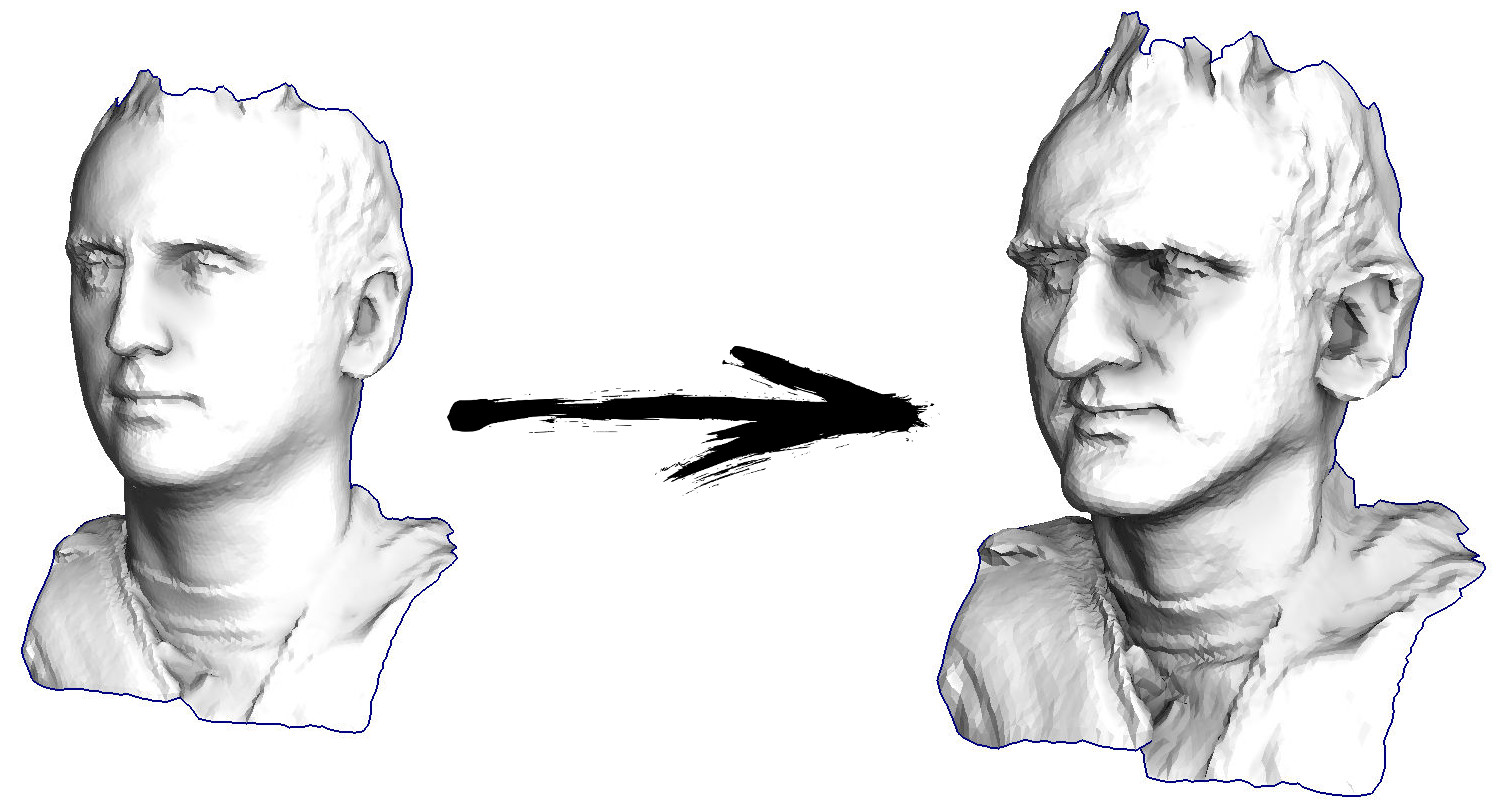
Dalam kasus khusus ini, saya memecahkan persamaan diferensial elips bernama Simeon Demi Poisson . Rekan-rekan programmer, mari kita bermain game: tebak berapa banyak baris yang ada dalam kode C ++ yang memutuskannya? Perpustakaan pihak ketiga tidak dapat dipanggil, kami hanya memiliki kompiler kosong yang kami miliki. Jawabannya ada di bawah potongan.

Bahkan, dua puluh baris kode sudah cukup untuk seorang pemecah masalah. Jika Anda menghitung dengan semuanya, semuanya, termasuk parser dari file model 3D, maka simpan dalam dua ratus baris - cukup ludah.

Contoh 1: perataan data

Mari kita bicara tentang cara kerjanya. Mari kita mulai dari jauh, bayangkan kita memiliki array reguler f, misalnya, dari 32 elemen, diinisialisasi sebagai berikut:



Dan kemudian kita akan melakukan prosedur berikut ini ribuan kali: untuk setiap sel f [i] kita menuliskan nilai rata-rata sel tetangga ke dalamnya: f [i] = (f [i-1] + f [i + 1]) / 2. Untuk membuatnya lebih jelas, berikut ini adalah kode lengkap:

import matplotlib.pyplot as plt f = [0.] * 32 f[0] = f[-1] = 1. f[18] = 2. plt.plot(f, drawstyle='steps-mid') for iter in range(1000): f[0] = f[1] for i in range(1, len(f)-1): f[i] = (f[i-1]+f[i+1])/2. f[-1] = f[-2] plt.plot(f, drawstyle='steps-mid') plt.show() 

Setiap iterasi akan memuluskan data array kami, dan setelah seribu iterasi kami akan mendapatkan nilai konstan di semua sel. Inilah animasi dari seratus lima puluh iterasi pertama:



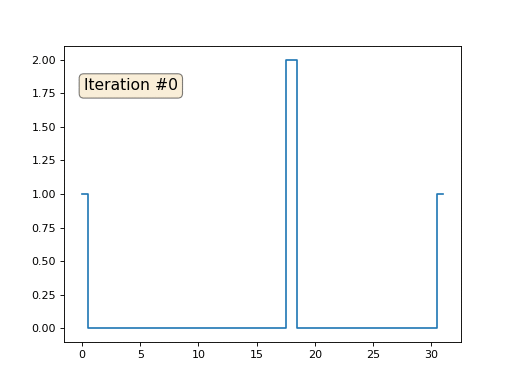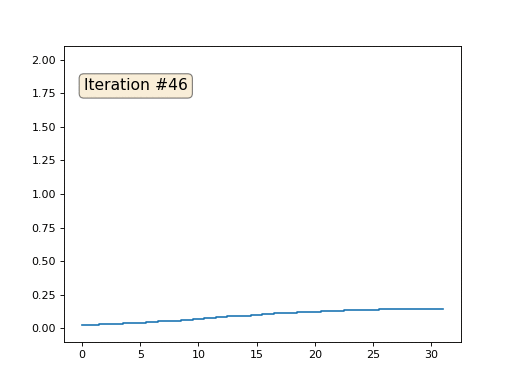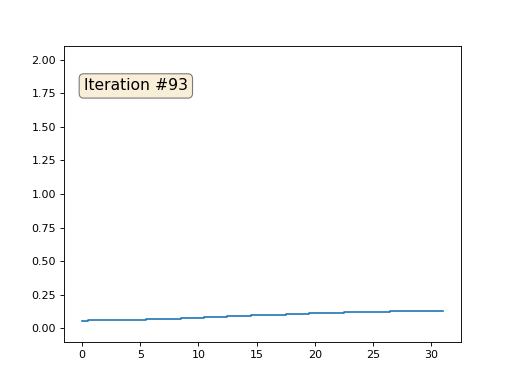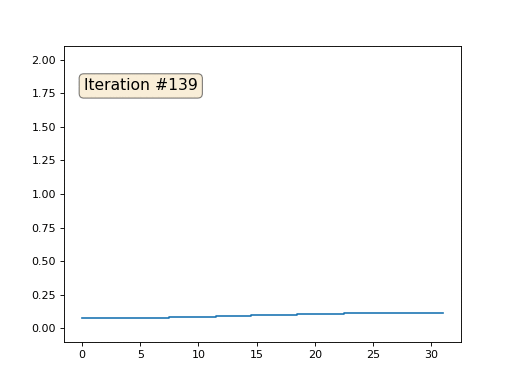
Jika tidak jelas bagi Anda mengapa anti-aliasing terjadi, berhentilah sekarang, ambil pena dan cobalah untuk menggambar contoh, jika tidak masuk akal untuk membaca lebih lanjut. Permukaan triangulasi pada dasarnya sama dengan contoh ini. Bayangkan bahwa untuk setiap simpul kita temukan tetangganya, hitung pusat massa mereka, dan pindahkan simpul kita ke pusat massa ini, dan sepuluh kali lipat. Hasilnya akan seperti ini:



Tentu saja, jika Anda tidak berhenti di sepuluh iterasi, maka setelah beberapa saat seluruh permukaan akan dikompresi ke satu titik dengan cara yang persis sama seperti pada contoh sebelumnya, seluruh array menjadi terisi dengan nilai yang sama.

Contoh 2: meningkatkan / melemahkan fitur

Kode lengkap tersedia di github , tetapi di sini saya akan memberikan bagian yang paling penting, hanya menghilangkan membaca dan menulis model 3D. Jadi, model triangulasi bagi saya diwakili oleh dua array: verts dan wajah. Array verts hanya seperangkat titik tiga dimensi, mereka adalah simpul dari poligon mesh. Array wajah adalah seperangkat segitiga (jumlah segitiga sama dengan wajah. Ukuran ()), untuk setiap segitiga indeks dari array vertex disimpan dalam array. Format data dan bekerja dengannya saya jelaskan secara rinci dalam kuliah saya tentang grafik komputer. Ada juga array ketiga, yang saya hitung dari dua yang pertama (lebih tepatnya, hanya dari array wajah) - vvadj. Ini adalah larik yang untuk setiap simpul (indeks pertama dari array dua dimensi) menyimpan indeks tetangganya (indeks kedua).

 std::vector<Vec3f> verts; std::vector<std::vector<int> > faces; std::vector<std::vector<int> > vvadj; 

Hal pertama yang saya lakukan adalah untuk setiap titik permukaan saya, saya mempertimbangkan vektor kelengkungan. Mari kita ilustrasikan: untuk vertex saat ini, saya beralih pada semua tetangganya n1-n4; maka saya menghitung pusat massa mereka b = (n1 + n2 + n3 + n4) / 4. Nah, vektor kelengkungan akhir dapat dihitung sebagai c = vb, itu tidak seperti perbedaan hingga biasa untuk turunan kedua .



Langsung dalam kode, terlihat seperti ini:

  std::vector<Vec3f> curvature(verts.size(), Vec3f(0,0,0)); for (int i=0; i<(int)verts.size(); i++) { for (int j=0; j<(int)vvadj[i].size(); j++) { curvature[i] = curvature[i] - verts[vvadj[i][j]]; } curvature[i] = verts[i] + curvature[i] / (float)vvadj[i].size(); } 

Nah, maka kita melakukan hal berikut berkali-kali (lihat gambar sebelumnya): kita pindahkan vertex v ke v: = b + const * c. Harap dicatat bahwa jika konstanta sama dengan satu, maka titik kami tidak akan bergerak ke mana pun! Jika konstanta adalah nol, maka simpul diganti oleh pusat massa dari simpul tetangga, yang akan menghaluskan permukaan kita. Jika konstanta lebih besar dari satu (gambar judul dibuat menggunakan const = 2.1), maka titik akan bergeser ke arah vektor kelengkungan permukaan, memperkuat detail. Beginilah tampilannya dalam kode:

  for (int it=0; it<100; it++) { for (int i=0; i<(int)verts.size(); i++) { Vec3f bary(0,0,0); for (int j=0; j<(int)vvadj[i].size(); j++) { bary = bary + verts[vvadj[i][j]]; } bary = bary / (float)vvadj[i].size(); verts[i] = bary + curvature[i]*2.1; // play with the coeff here } } 

Omong-omong, jika kurang dari satu, maka rinciannya akan melemah sebaliknya (const = 0,5), tetapi ini tidak akan setara dengan smoothing sederhana, "kontras gambar" akan tetap:



Harap dicatat bahwa kode saya menghasilkan file model 3D dalam format .obj Wavefront , saya render dalam program pihak ketiga. Anda dapat melihat model yang dihasilkan, misalnya, di penampil online . Jika Anda tertarik pada metode rendering, daripada menghasilkan model, maka baca kursus saya di grafik komputer .

Contoh 3: menambah kendala

Mari kita kembali ke contoh pertama, dan melakukan hal yang persis sama, tetapi tidak akan menulis ulang elemen array di bawah angka 0, 18 dan 31:

 import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. plt.plot(x, drawstyle='steps-mid') plt.show() 

Saya menginisialisasi sisanya, elemen "bebas" dari array dengan nol, dan masih secara iteratif menggantinya dengan nilai rata-rata elemen tetangga. Ini adalah bagaimana evolusi array terlihat seperti dalam seratus lima puluh iterasi pertama:



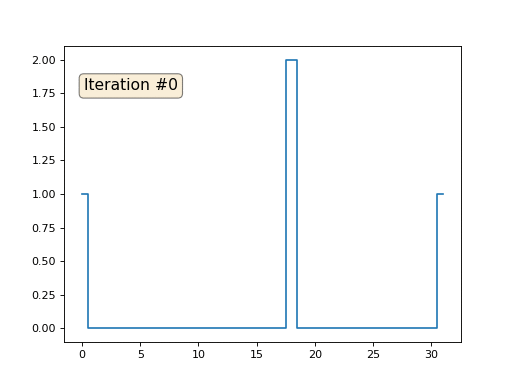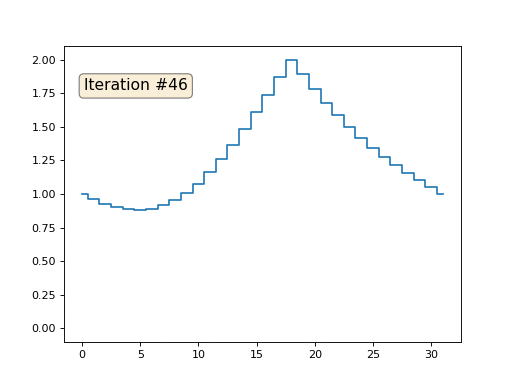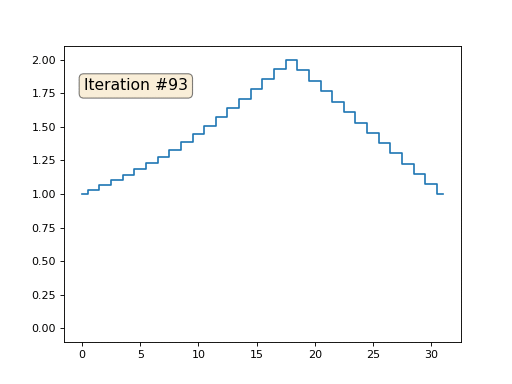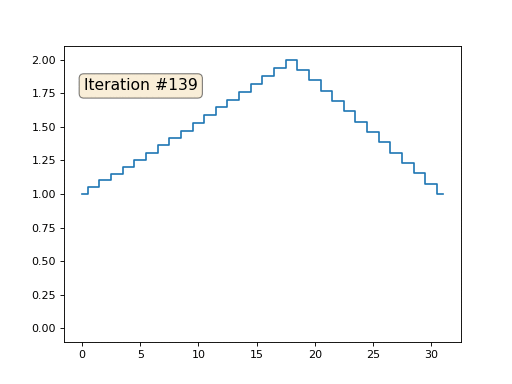
Cukup jelas bahwa kali ini solusinya akan bertemu bukan dengan elemen konstan yang mengisi array, tetapi untuk dua jalur linier. Omong-omong, apakah itu benar-benar jelas bagi semua orang? Jika tidak, maka bereksperimen dengan kode ini, saya secara khusus memberikan contoh dengan kode yang sangat singkat sehingga Anda dapat benar-benar memahami apa yang terjadi.

Penyimpangan liris: solusi numerik sistem persamaan linear.

Mari kita diberi sistem persamaan linear biasa:



Itu dapat ditulis ulang, meninggalkan di setiap persamaan di satu sisi tanda sama dengan x_i:



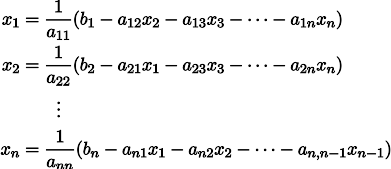
Mari kita diberi vektor yang sewenang-wenang mendekati solusi sistem persamaan (misalnya, nol).

Kemudian, dengan menempelkannya di sisi kanan sistem kami, kita bisa mendapatkan solusi vektor pendekatan yang diperbarui .

Untuk membuatnya lebih jelas, x1 diperoleh dari x0 sebagai berikut:



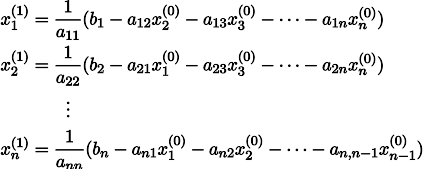
Mengulangi proses k kali, solusi akan didekati oleh vektor

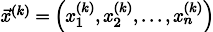
Mari berjaga-jaga, tulis rumus rekursi:



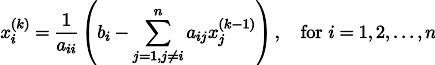
Di bawah beberapa asumsi tentang koefisien sistem (misalnya, jelas bahwa elemen diagonal tidak boleh nol, karena kami membaginya), prosedur ini menyatu dengan solusi yang sebenarnya. Senam ini dikenal dalam literatur sebagai metode Jacobi . Tentu saja, ada metode lain untuk menyelesaikan sistem persamaan linear secara numerik, dan yang jauh lebih kuat, misalnya, metode gradien konjugat , tetapi mungkin metode Jacobi adalah salah satu yang paling sederhana.

Contoh 3 lagi, tetapi di sisi lain

Dan sekarang mari kita lihat lebih dekat loop utama dari Contoh 3:

 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. 

Saya mulai dengan beberapa vektor x awal, dan saya memperbaruinya seribu kali, dan prosedur pembaruannya mencurigakan mirip dengan metode Jacobi! Mari kita menulis sistem persamaan ini secara eksplisit:



Luangkan sedikit waktu, pastikan setiap iterasi dalam kode Python saya hanya satu pembaruan dari metode Jacobi untuk sistem persamaan ini. Nilai x [0], x [18] dan x [31] ditetapkan untuk saya, masing-masing, mereka tidak termasuk dalam set variabel, oleh karena itu mereka ditransfer ke sisi kanan.

Secara total, semua persamaan dalam sistem kami terlihat seperti - x [i-1] + 2 x [i] - x [i + 1] = 0. Ungkapan ini tidak lebih dari perbedaan hingga biasa untuk turunan kedua . Yaitu, sistem persamaan kami hanya menetapkan bahwa turunan kedua harus sama dengan nol di mana-mana (well, kecuali pada titik x [18]). Ingat, saya mengatakan bahwa jelas bahwa iterasi harus bertemu dengan jalur landai? Itulah tepatnya mengapa turunan linier dari turunan kedua adalah nol.

Apakah Anda tahu bahwa kami baru saja menyelesaikan masalah Dirichlet untuk persamaan Laplace ?

Ngomong-ngomong, seorang pembaca yang penuh perhatian seharusnya memperhatikan bahwa, secara tegas, dalam kode saya, sistem persamaan linear diselesaikan bukan dengan metode Jacobi, tetapi dengan metode Gauss-Seidel , yang merupakan semacam optimasi metode Jacobi:

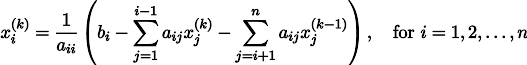
Contoh 4: Persamaan Poisson

Dan mari kita ubah contoh ketiga sedikit saja: setiap sel ditempatkan tidak hanya di pusat massa sel tetangga, tetapi di pusat massa ditambah beberapa konstanta (arbitrer):

 import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1] +11./32**2 )/2. plt.plot(x, drawstyle='steps-mid') plt.show() 

Dalam contoh sebelumnya, kami menemukan bahwa menempatkan di pusat massa adalah diskritisasi operator Laplace (dalam kasus kami, turunan kedua). Artinya, sekarang kami sedang memecahkan sistem persamaan yang mengatakan bahwa sinyal kami harus memiliki turunan kedua yang konstan. Derivatif kedua adalah kelengkungan permukaan; dengan demikian, fungsi piecewise-kuadrat harus menjadi solusi untuk sistem kami. Mari kita periksa pengambilan sampel dalam 32 sampel:



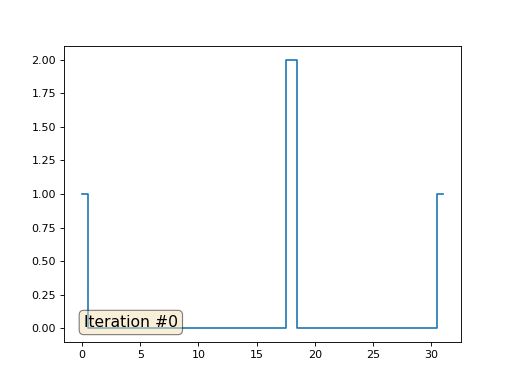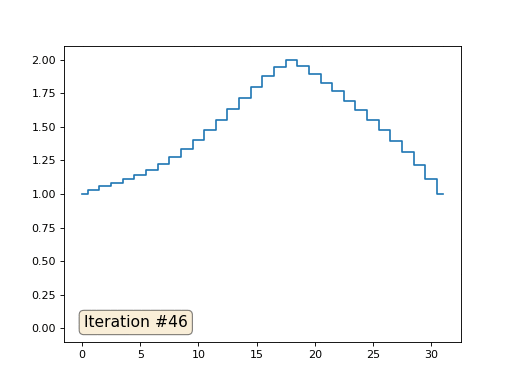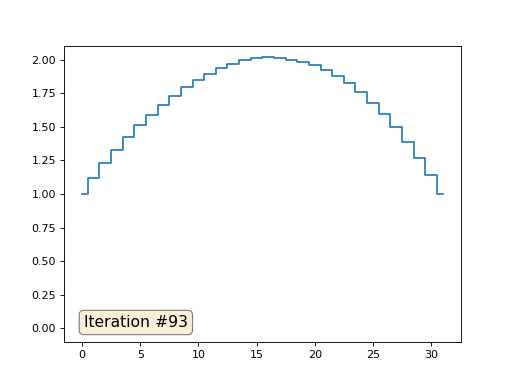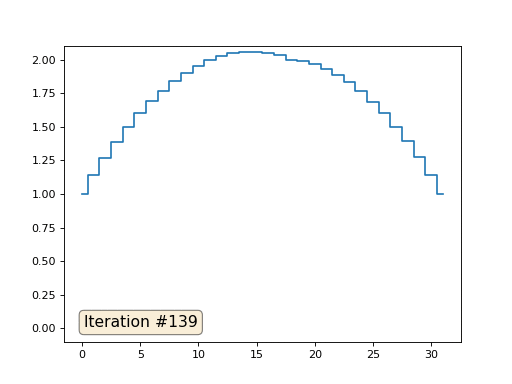
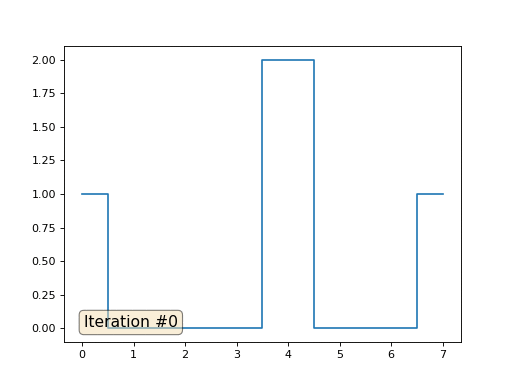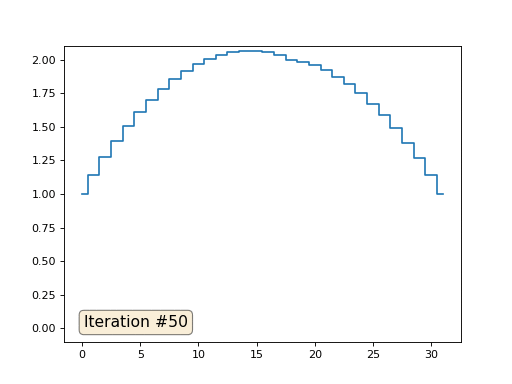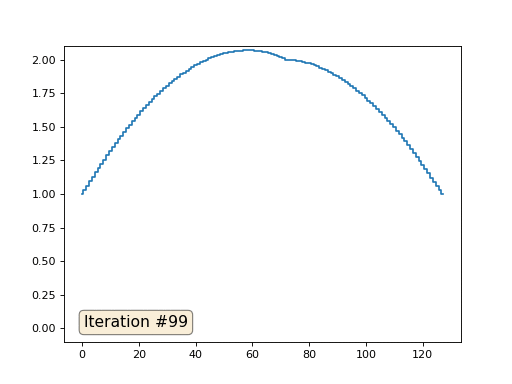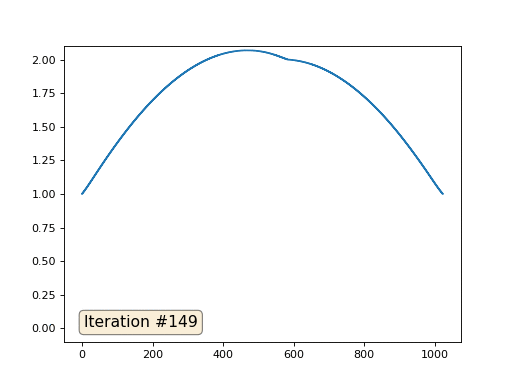
Dengan panjang array 32 elemen, sistem kami menyatu ke solusi dalam beberapa ratus iterasi. Tetapi bagaimana jika kita mencoba array dari 128 elemen? Semuanya jauh lebih menyedihkan di sini, jumlah iterasi harus sudah dihitung dalam ribuan:



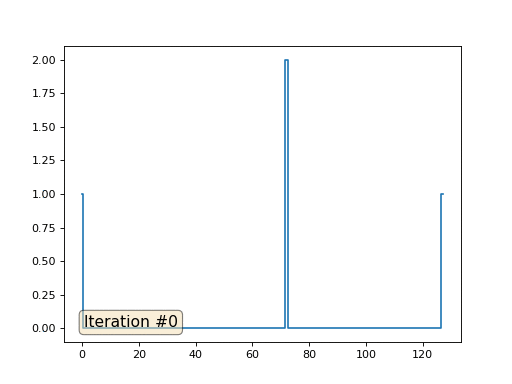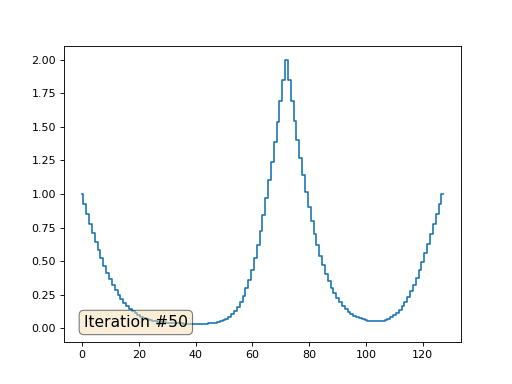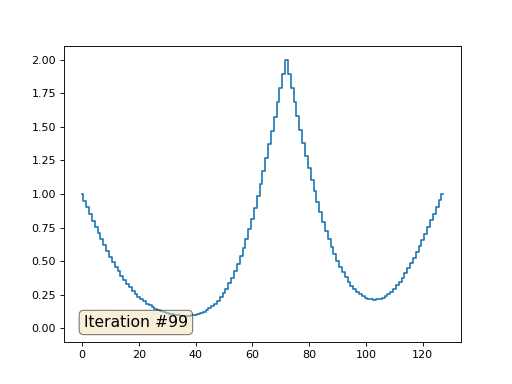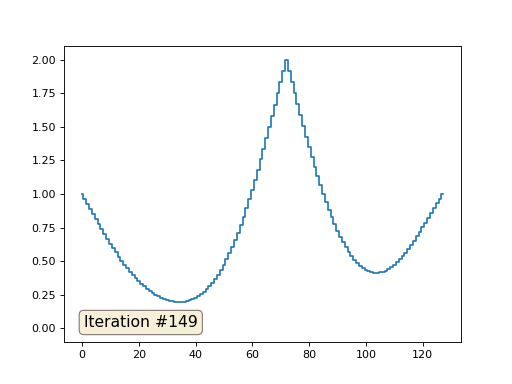
Metode Gauss-Seidel sangat sederhana untuk diprogram, tetapi tidak berlaku untuk sistem persamaan besar. Anda dapat mencoba mempercepatnya, menggunakan, misalnya, metode multigrid . Dalam kata-kata, ini mungkin terdengar rumit, tetapi idenya sangat primitif: jika kita menginginkan solusi dengan resolusi seribu elemen, pertama kita dapat menyelesaikannya dengan sepuluh elemen, mendapatkan perkiraan kasar, kemudian menggandakan resolusi, menyelesaikannya lagi, dan seterusnya, hingga kita mencapai hasil yang diinginkan. Dalam praktiknya, tampilannya seperti ini:



Dan Anda tidak bisa pamer, dan menggunakan pemecah nyata sistem persamaan. Jadi saya memecahkan contoh yang sama dengan membangun matriks A dan kolom b, kemudian menyelesaikan persamaan matriks Ax = b:

 import numpy as np import matplotlib.pyplot as plt n=1000 x = [0.] * n x[0] = x[-1] = 1. m = n*57//100 x[m] = 2. A = np.matrix(np.zeros((n, n))) for i in range(1,n-2): A[i, i-1] = -1. A[i, i] = 2. A[i, i+1] = -1. A = A[1:-2,1:-2] A[m-2,m-1] = 0 A[m-1,m-2] = 0 b = np.matrix(np.zeros((n-3, 1))) b[0,0] = x[0] b[m-2,0] = x[m] b[m-1,0] = x[m] b[-1,0] = x[-1] for i in range(n-3): b[i,0] += 11./n**2 x2 = ((np.linalg.inv(A)*b).transpose().tolist()[0]) x2.insert(0, x[0]) x2.insert(m, x[m]) x2.append(x[-1]) plt.plot(x2, drawstyle='steps-mid') plt.show() 

Dan di sini adalah hasil kerja program ini, perhatikan bahwa solusinya ternyata langsung:



Jadi, memang, fungsi kita adalah kuadratik piecewise (turunan kedua adalah konstan). Pada contoh pertama, kami menetapkan turunan kedua kedua ke nol, ketiga bukan nol, tetapi sama di mana-mana. Dan apa yang ada dalam contoh kedua? Kami memecahkan persamaan Poisson diskrit dengan menentukan kelengkungan permukaan. Biarkan saya mengingatkan Anda apa yang terjadi: kami menghitung kelengkungan permukaan yang masuk. Jika kita memecahkan masalah Poisson dengan mengatur kelengkungan permukaan pada output sama dengan kelengkungan permukaan pada input (const = 1), maka tidak ada yang akan berubah. Penguatan fitur wajah terjadi ketika kita hanya meningkatkan kelengkungan (const = 2.1). Dan jika const <1, maka kelengkungan permukaan yang dihasilkan berkurang.

Perbarui: mainan lain sebagai pekerjaan rumah

Mengembangkan ide yang disarankan oleh SquareRootOfZero , bermain-main dengan kode ini:



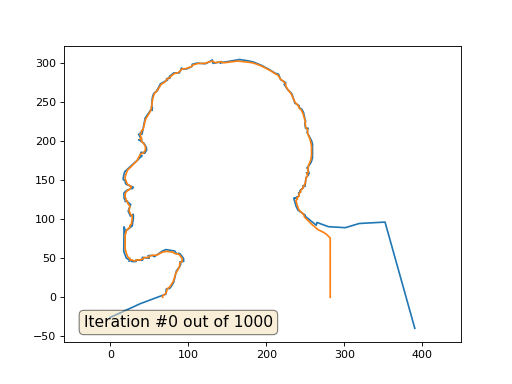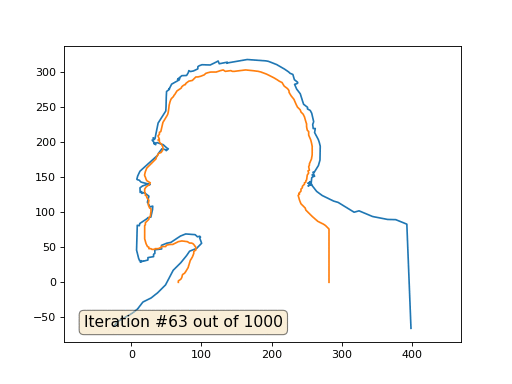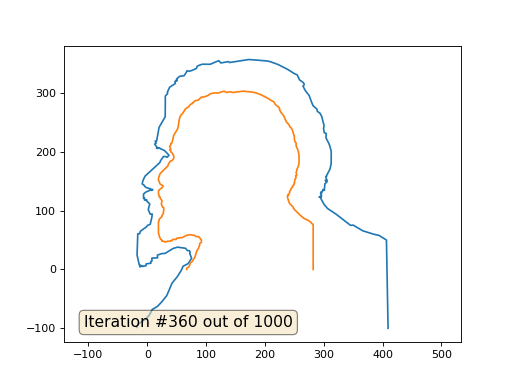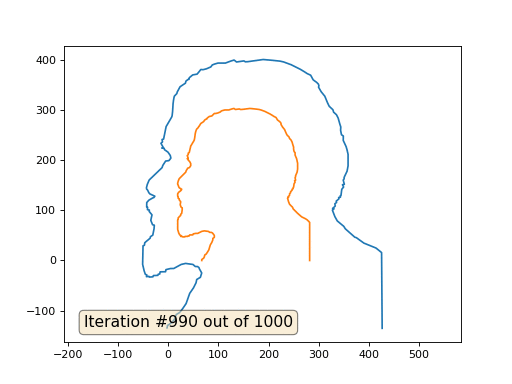
Ini adalah hasil default, Lenin merah adalah data awal, kurva biru adalah evolusi mereka, hingga tak terbatas hasilnya konvergen ke titik:



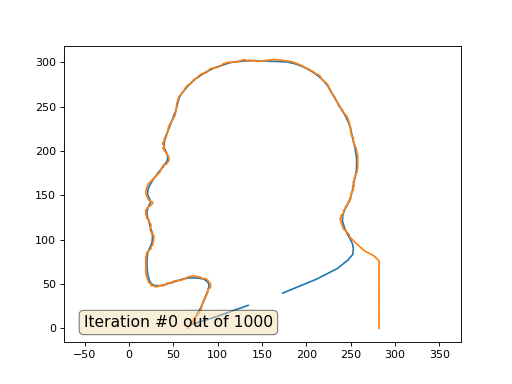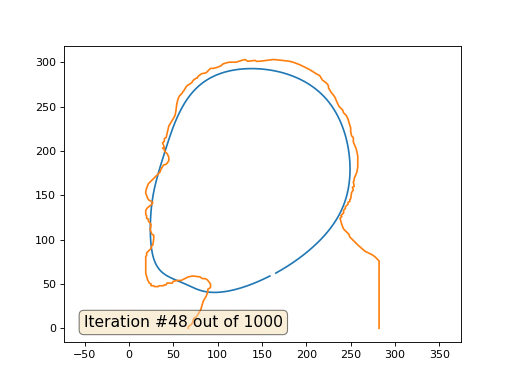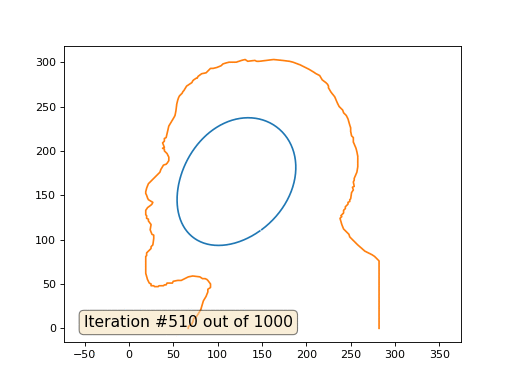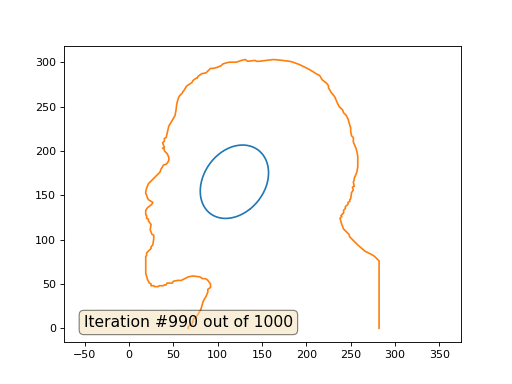
Dan ini hasilnya dengan koefisien 2::



Pekerjaan rumah: mengapa dalam kasus kedua, Lenin pertama berubah menjadi Dzerzhinsky, dan sekali lagi menyatu dengan Lenin, tetapi dengan ukuran yang lebih besar?

Kesimpulan

Banyak tugas pemrosesan data, khususnya, geometri, dapat dirumuskan sebagai solusi untuk sistem persamaan linear. Dalam artikel ini saya tidak memberi tahu bagaimana membangun sistem ini, tujuan saya hanya untuk menunjukkan bahwa ini mungkin. Topik artikel berikutnya tidak lagi menjadi “mengapa,” tetapi “bagaimana,” dan pemecah mana yang akan digunakan nanti.

By the way, dan setelah semua dalam judul artikel paling tidak ada kotak. Apakah Anda melihatnya dalam teks? Jika tidak, maka ini sama sekali tidak menakutkan, ini adalah jawaban tepat untuk pertanyaan "bagaimana?". Tetap terhubung, di artikel berikutnya saya akan menunjukkan dengan tepat di mana mereka bersembunyi, dan bagaimana memodifikasinya untuk mendapatkan akses ke alat pengolah data yang sangat kuat. Misalnya, dalam sepuluh baris kode Anda bisa mendapatkan ini:



Nantikan lebih lanjut!