Proses gelombang dalam saluran hidrolik. Dasar-dasarnya

Halo, Habr!

Dalam artikel sebelumnya saya berbicara tentang metode karakteristik, yang dirancang untuk menghitung proses gelombang di saluran hidrolik. Bahkan, tentu saja, proses gelombang dapat dihitung dalam pikiran, Anda hanya perlu tahu pendekatannya.

Di bawah luka, saya akan menunjukkan "pada jari" dan dengan bantuan gif efek gelombang utama. Sebagai contoh, saya akan kembali menggunakan saluran hidrolik, tetapi pada kenyataannya, mereka didasarkan pada persamaan yang hampir sama seperti untuk akustik dan saluran listrik. Jadi, bahkan jika Anda bukan hidrolik, mungkin ada analogi sederhana untuk membantu Anda memahami proses gelombang secara umum.

Perhatian Di bawah kucing 15 MB gif animasi!

Jadi, di sini kita akan mempertimbangkan perambatan gelombang pesawat satu dimensi dalam garis hidrolik. Asumsi ini cukup benar untuk pipa panjang, yang panjangnya berkali-kali lebih besar dari diameter bagian dalam. Untuk kesederhanaan, kami juga mengabaikan gesekan untuk saat ini. Dalam hal ini, proses fisik yang sedang berlangsung akan dijelaskan oleh sepasang persamaan diferensial parsial:

$$

$$\ frac {\ partial p} {\ partial t} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x} = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} = 0$$

dimana $$$\ rho$- kepadatan $$$v$- kecepatan $$$p$- tekanan $$$c$- kecepatan suara.

Karena kebiasaan, tampilan persamaan ini bisa menakutkan, tetapi pada kenyataannya, semuanya sederhana di sini. Persamaan pertama memberi tahu kita bahwa tekanan akan meningkat seiring waktu jika lebih banyak cairan mengalir ke segmen pipa daripada mengalir keluar (apalagi, semakin cepat semakin padat dan elastis cairan di dalam pipa); persamaan kedua menunjukkan bahwa untuk mempercepat segmen cairan, perlu menerapkan perbedaan tekanan padanya (apalagi, semakin besar densitas, semakin Anda perlu menerapkan perbedaan tekanan untuk mempercepat segmen). Yaitu hal-hal yang cukup dangkal dijelaskan: fluida itu dapat dimampatkan, fluida itu memiliki massa.
Mari kita tinggalkan solusi analitik dari persamaan ini untuk artikel yang akan datang, mari kita langsung beralih ke contoh “dengan jari”.
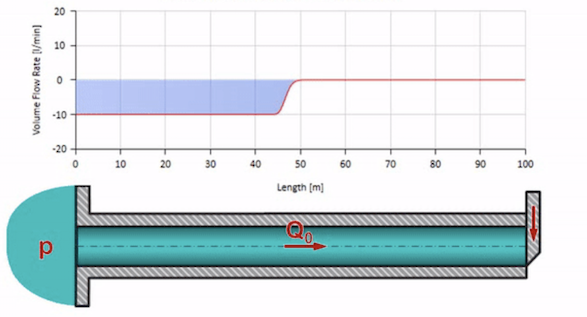
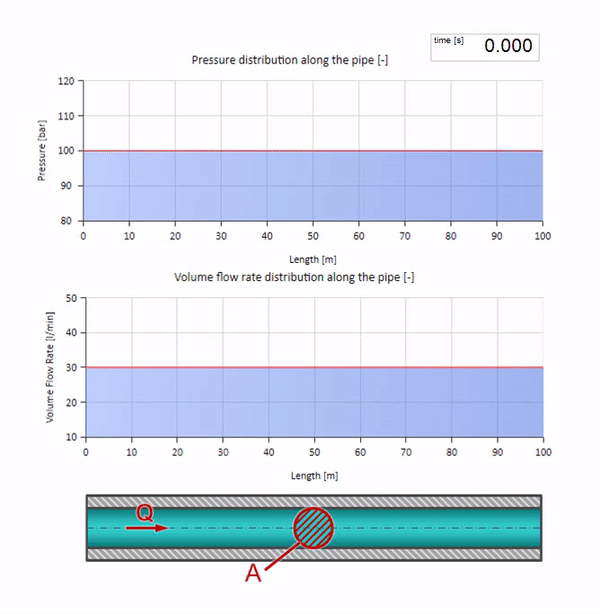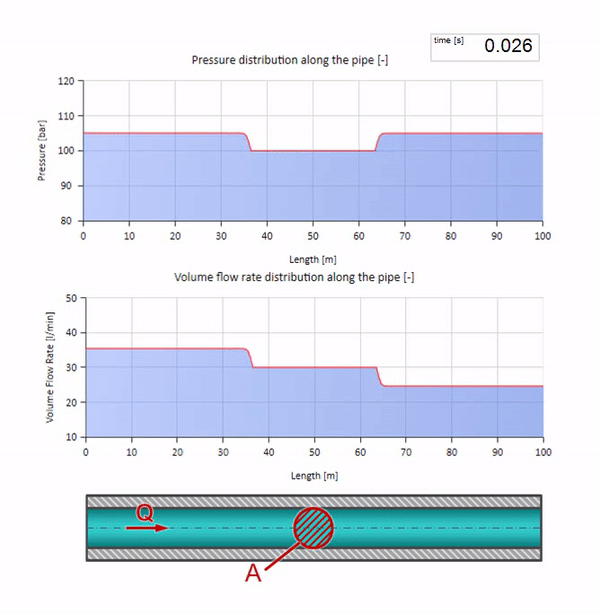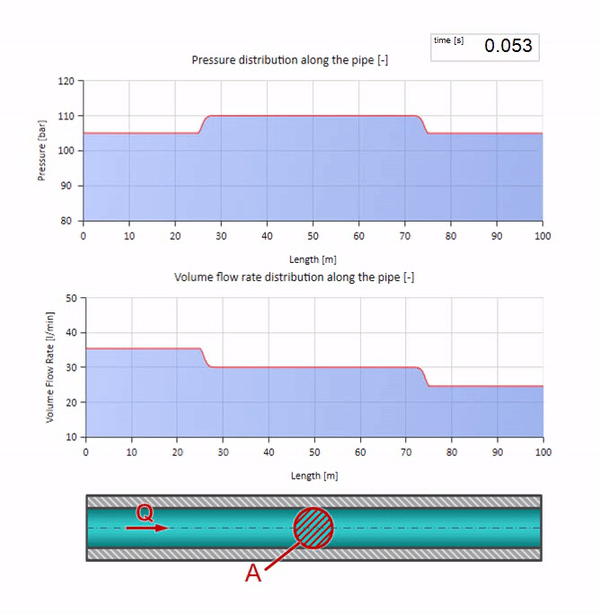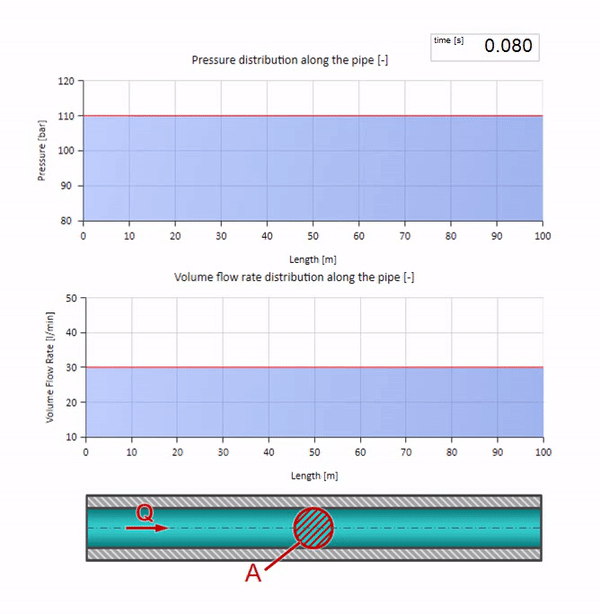
Ambil pipa yang diisi air dengan tekanan 100 bar (10 MPa) dipertahankan dan laju aliran 30 l / mnt mengalir. Jika langkah tekanan diterapkan ke ujung kiri, ia akan diprediksi mulai bergerak di sepanjang aliran dengan kecepatan yang sama dengan kecepatan suara dalam medium.

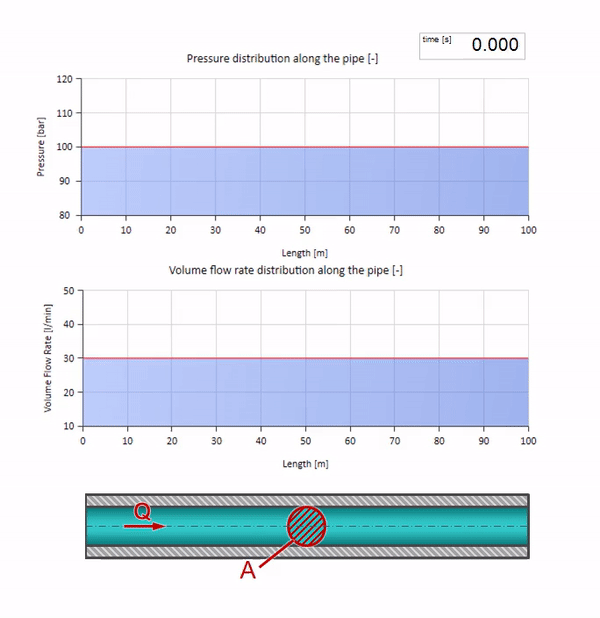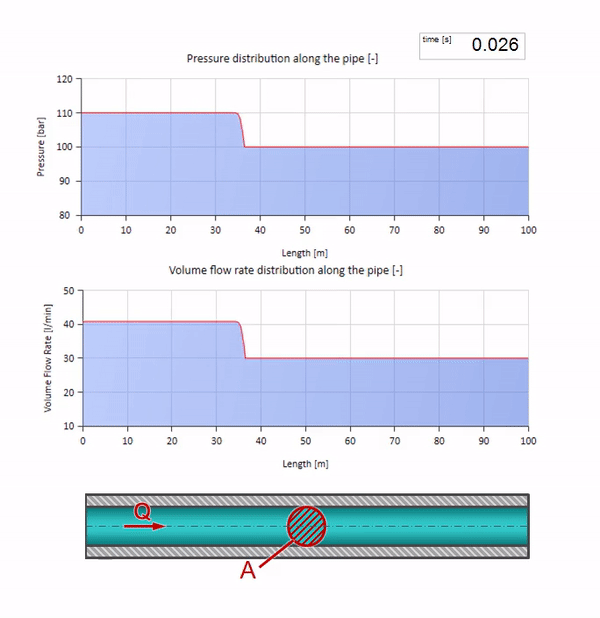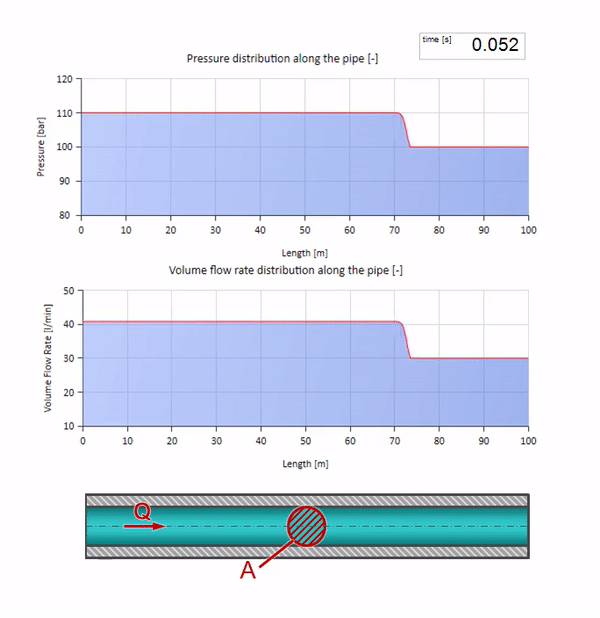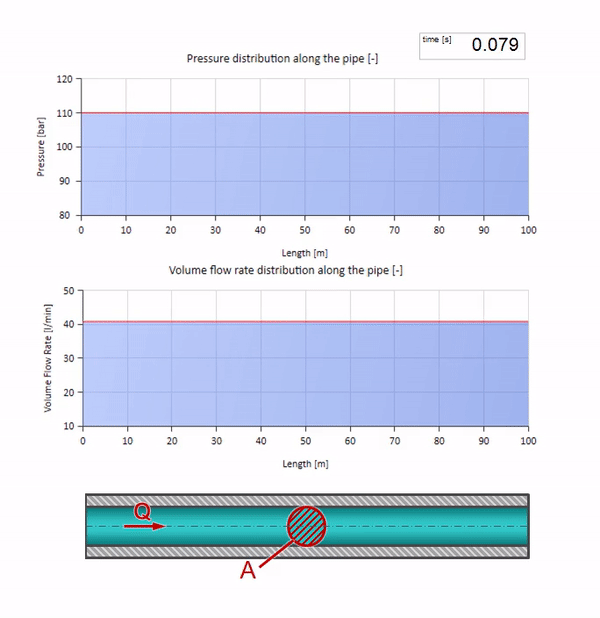
Tentu saja, dengan tekanan, laju aliran juga akan berubah. Jika tekanan naik, itu akan "menyesuaikan" fluida hulu dan meningkatkan laju aliran beberapa "langkah" juga. Berapa banyak ditentukan oleh nilai impedansi gelombang. Untuk pipa dengan luas penampang $$$A$diisi dengan cairan dengan kepadatan $$$\ rho$dan kecepatan suara lokal $$$c$, impedansi gelombang dapat dihitung sebagai berikut:

$$

$$Z_L = \ frac {\ rho \; c} A$$

Dalam hal dimensi, ini sama dengan tahanan hidrolik konvensional, hanya digunakan untuk menghitung rasio gelombang tekanan ( $$$\ widehat p$) dan laju aliran ( $$$\ widehat Q$), dan bukan nilai absolutnya:

$$

$$Z_L = \ frac {\ widehat p} {\ widehat Q}$$

Semakin besar kerapatan dan kecepatan suara, semakin tinggi impedansi gelombang, mis. semakin sulit untuk penurunan tekanan tertentu untuk membubarkan cairan (meningkatkan aliran)

Sekarang mari kita lihat bagaimana dua gelombang akan bergerak, bergerak menuju satu sama lain:

Jika tekanan di ujung kanan naik, fluida pasti akan terhambat oleh diferensial negatif. Ini berarti bahwa kenaikan tekanan gelombang yang terjadi terhadap aliran akan menyebabkan penurunan laju aliran dengan jumlah yang ditentukan lagi oleh hambatan gelombang. Artinya, gelombang pertumbuhan tekanan dan aliran jatuh akan bergerak di sebelah kanan.
Dalam tabrakan, mungkin terlihat bahwa gelombang aliran dipantulkan dari satu sama lain dan kembali. Bahkan, mereka hanya tumpang tindih. Efek ini juga disebut interferensi:

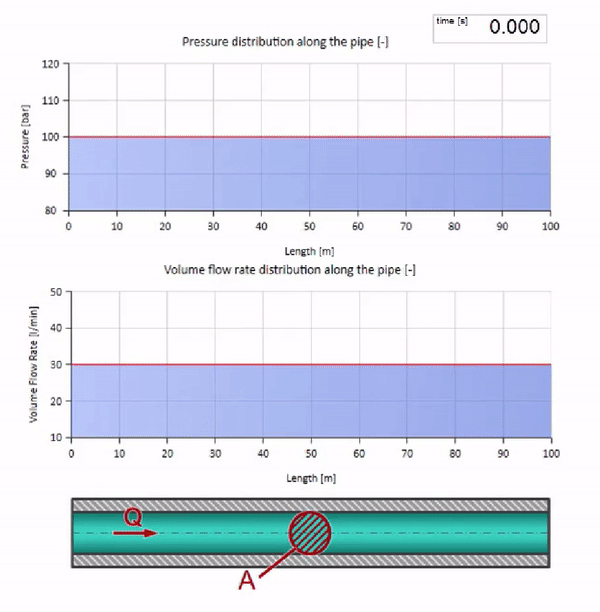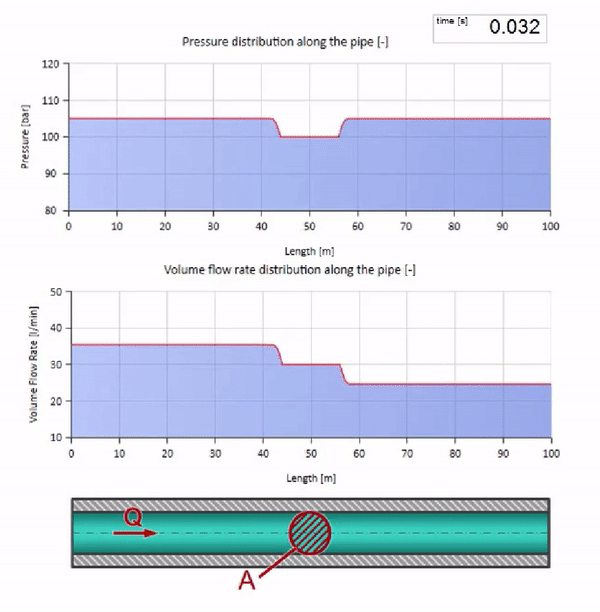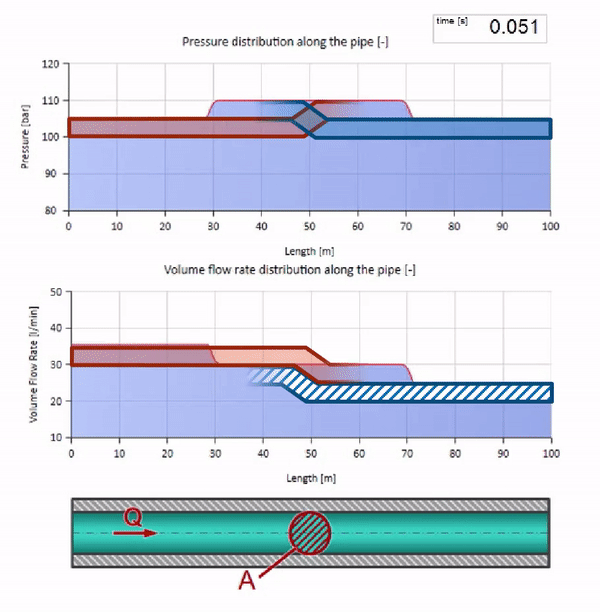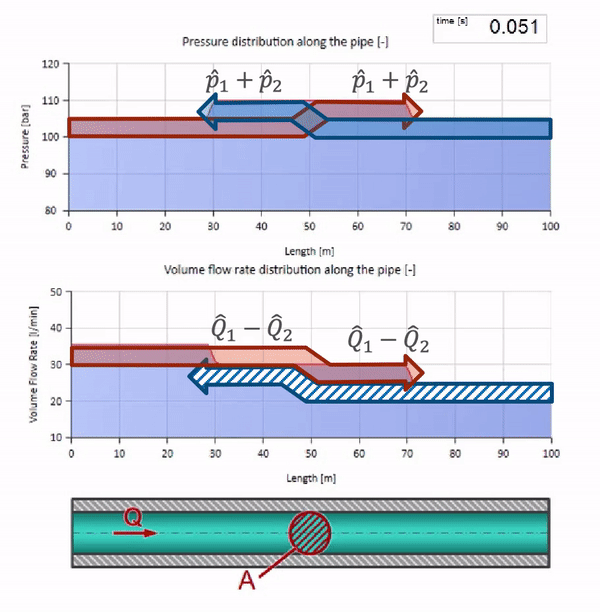
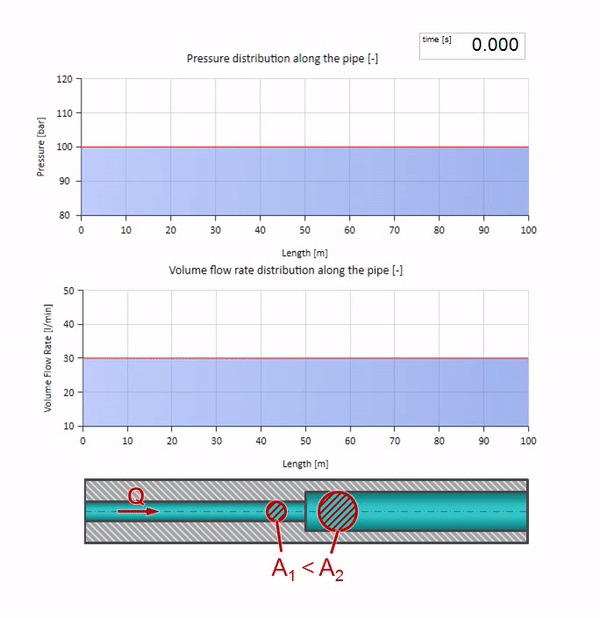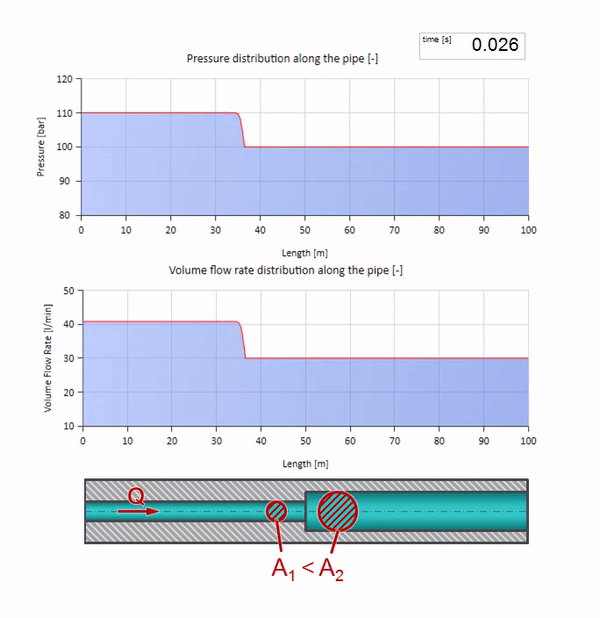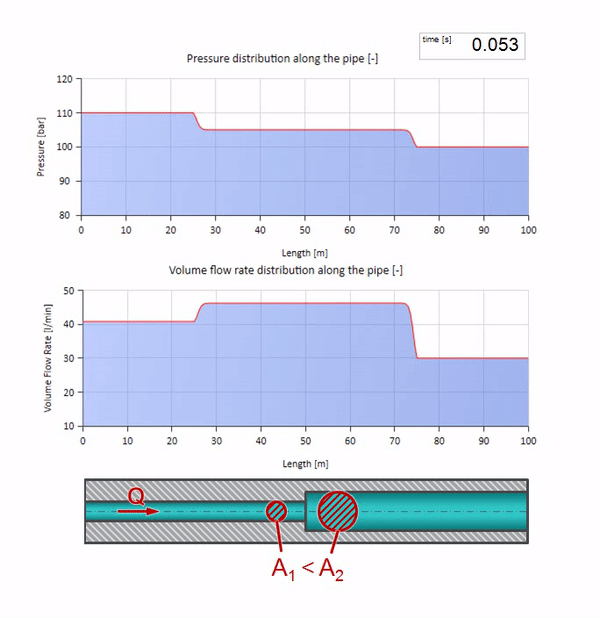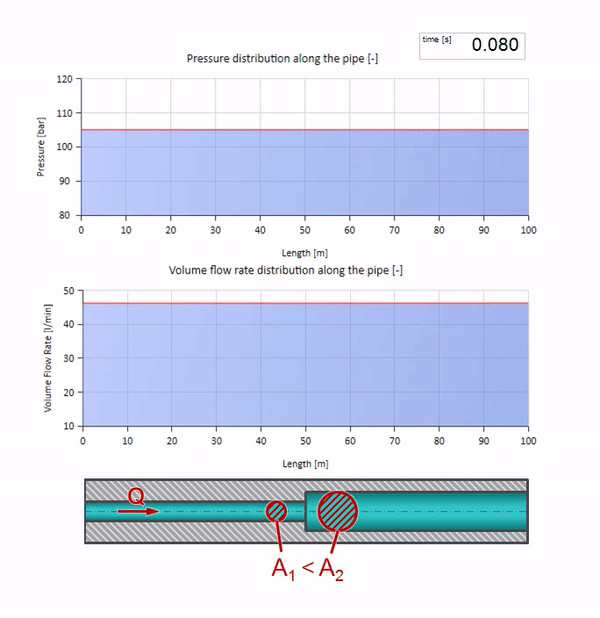
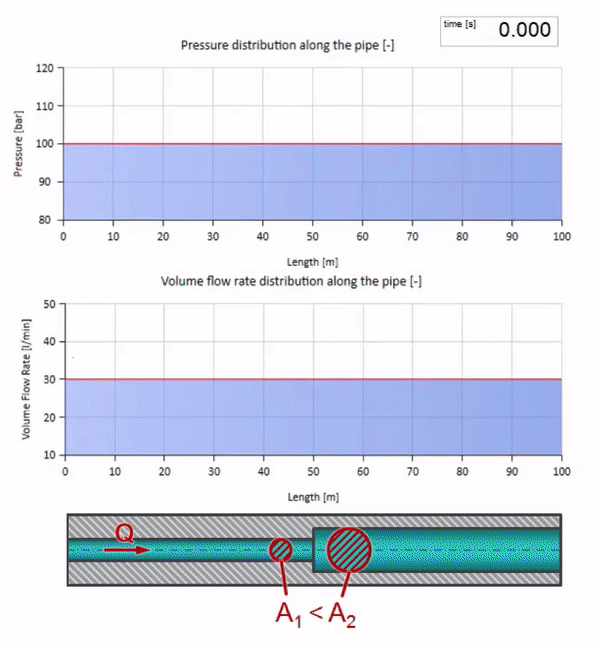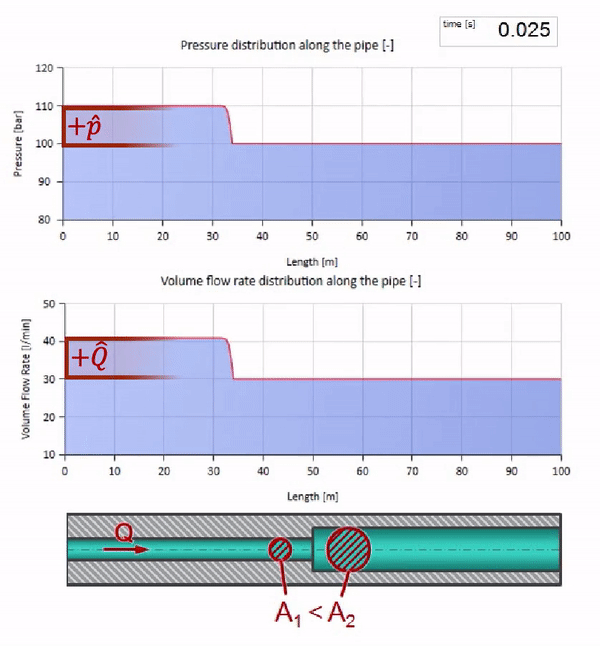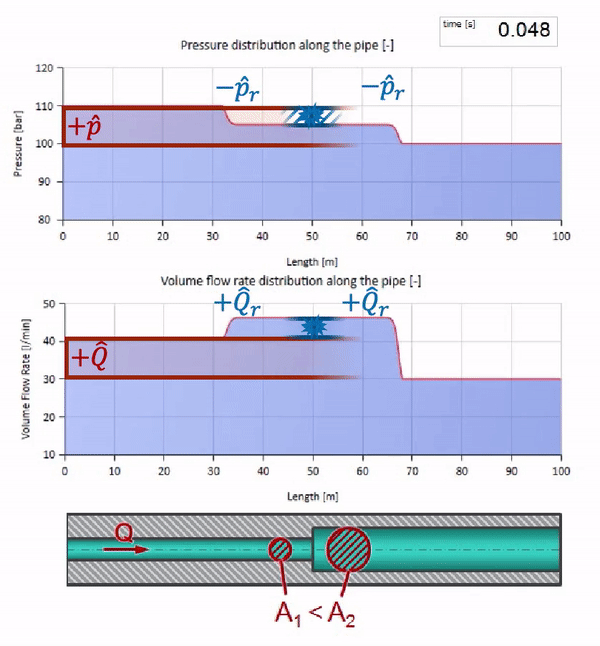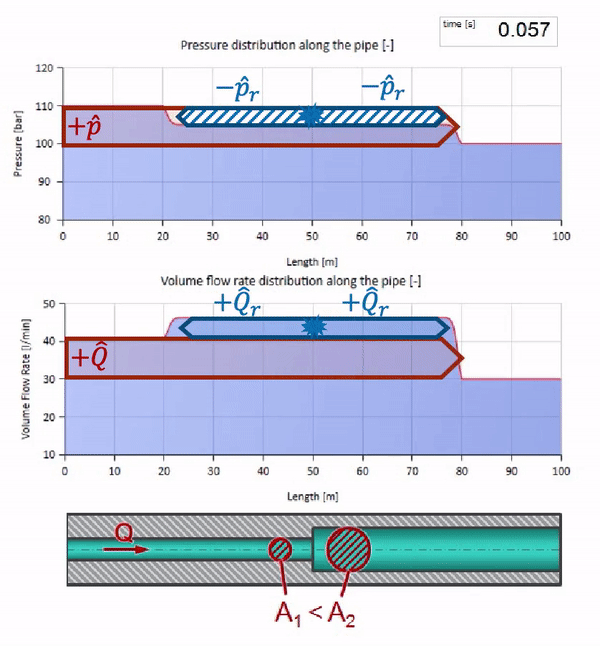
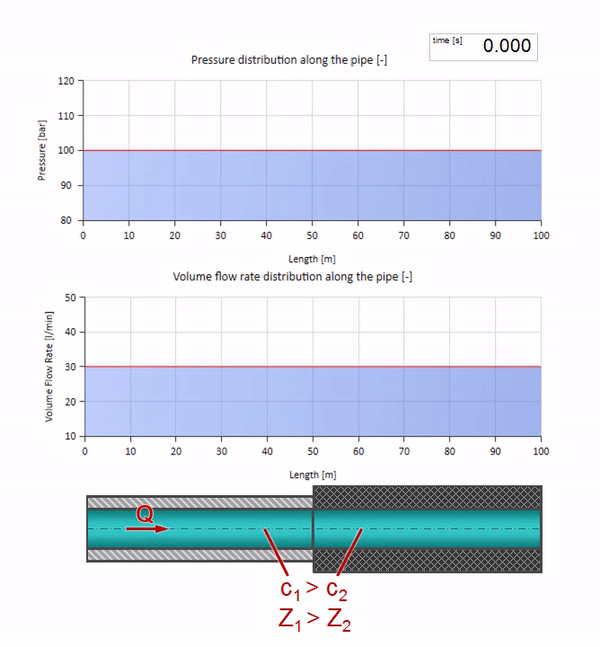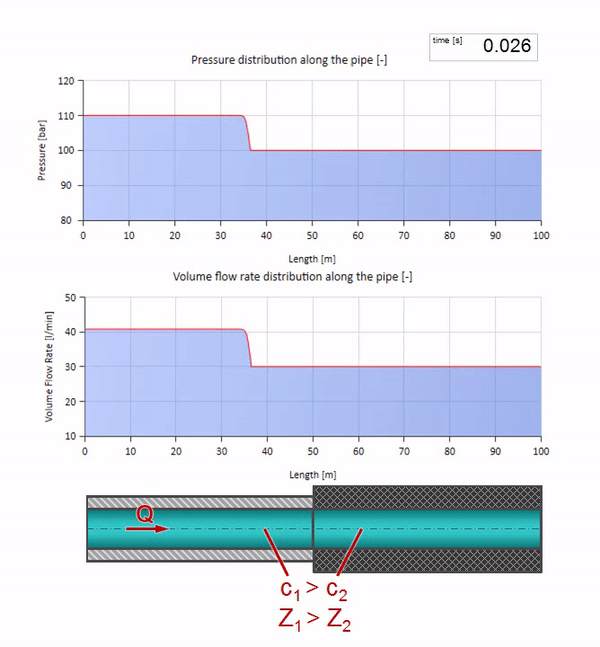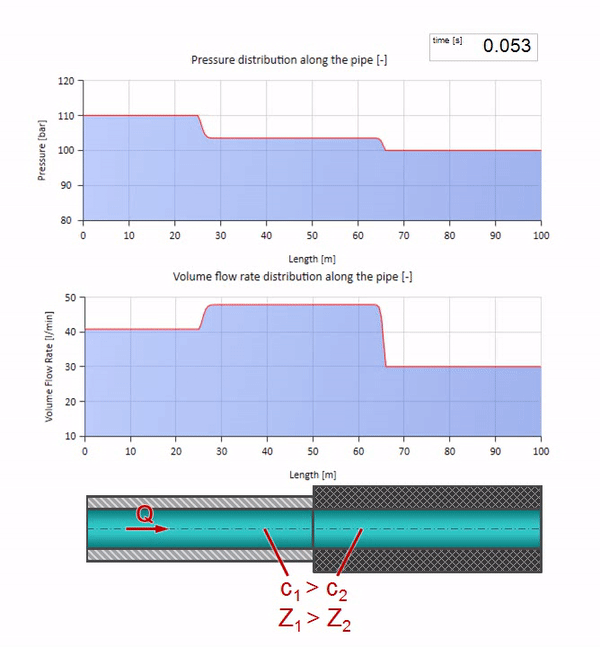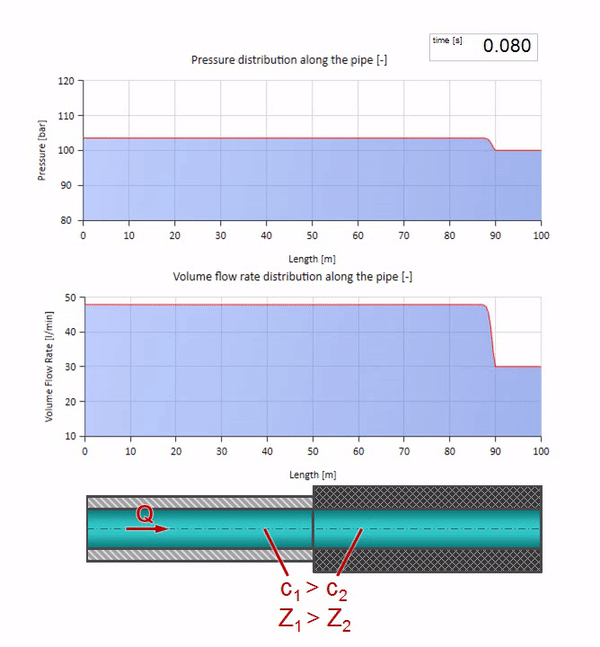
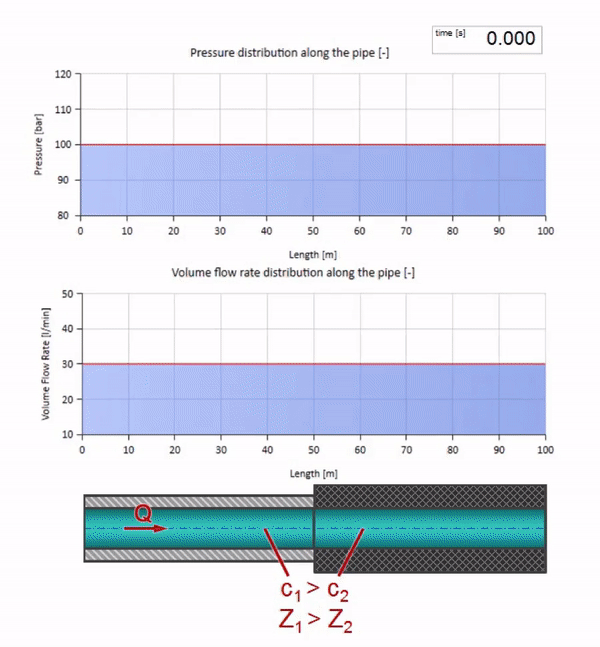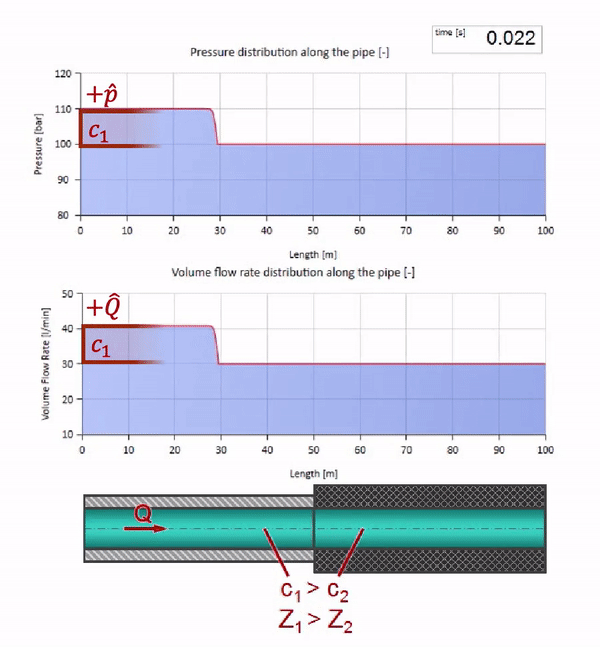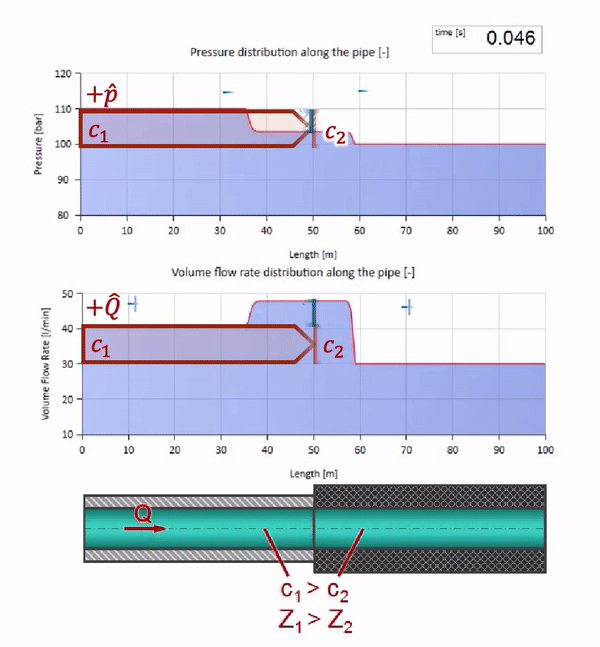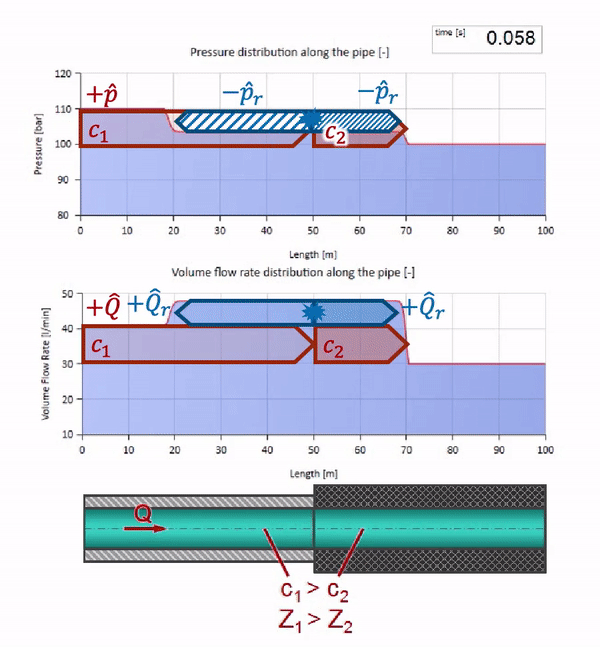
Sekarang kita tahu bahwa setiap pipa dengan cairan memiliki sifat seperti ketahanan gelombang. Sangat menarik untuk melihat apa yang akan terjadi pada gelombang jika diameter pipa di bagian tertentu berubah secara dramatis:

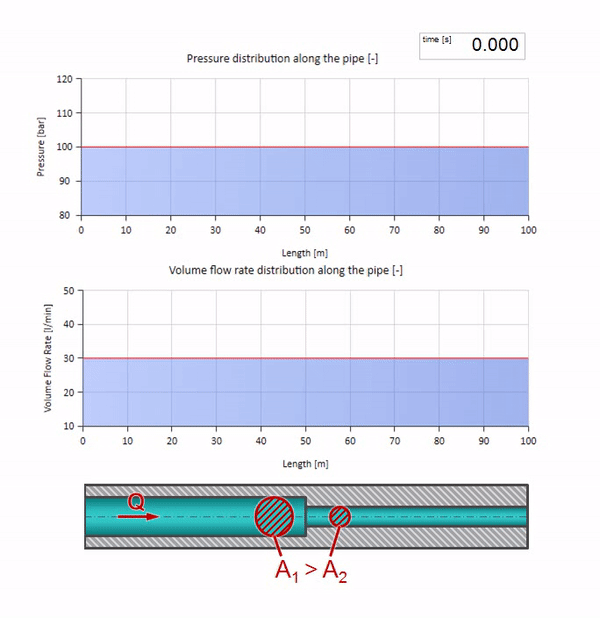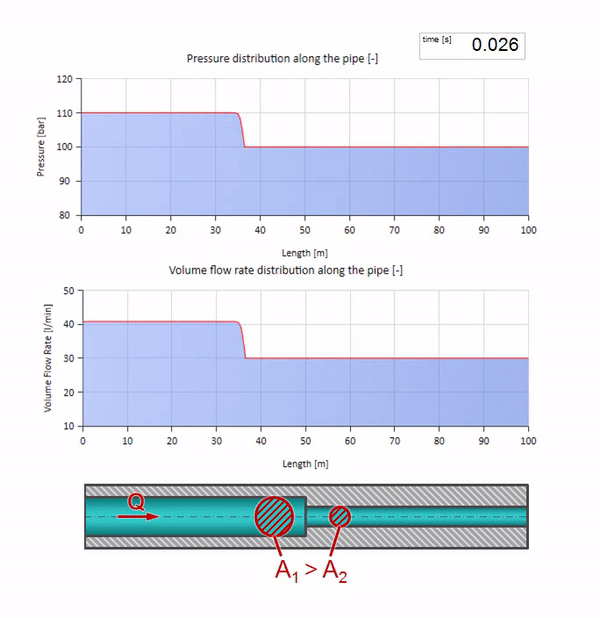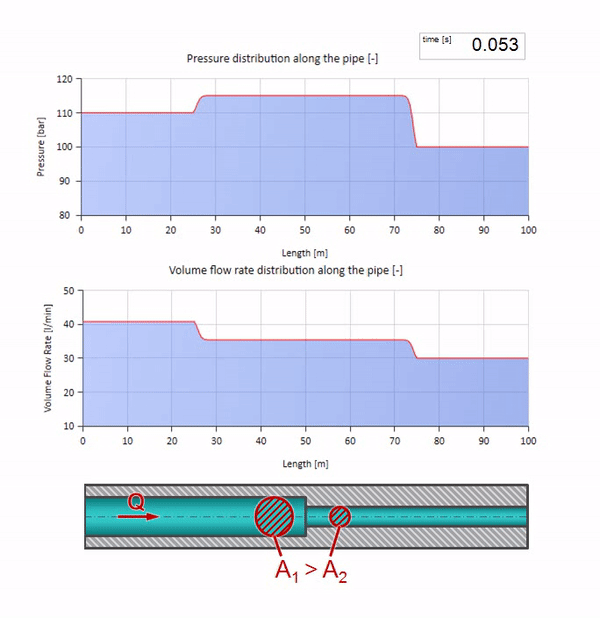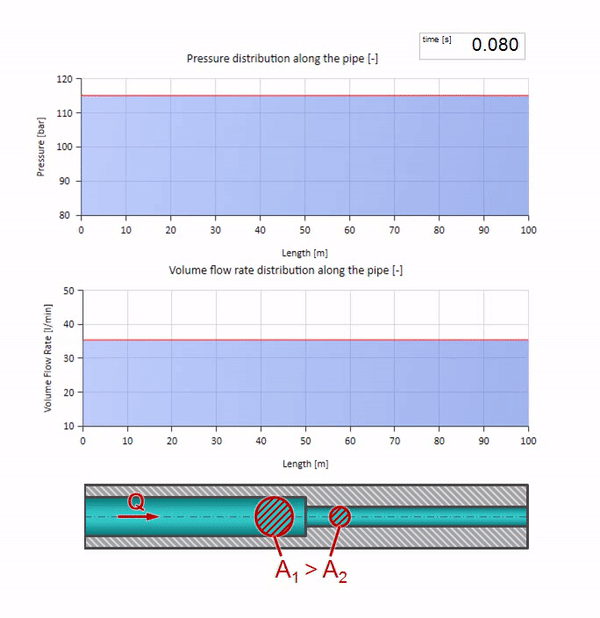
Sebelum gelombang mencapai tempat dengan penurunan diameter pipa, tentu saja, tidak ada yang menarik terjadi. Tetapi kemudian mencapai bagian dengan resistensi gelombang yang lebih tinggi, yang berarti bahwa rasio gelombang tekanan terhadap gelombang aliran harus lebih besar daripada di bagian kiri pipa. Ini berarti bahwa gelombang tekanan harus meningkat, dan laju aliran harus menurun. Pada saat yang sama, tidak ada yang tersisa untuk gelombang kecuali untuk menekuk ke kiri, sambil mempertahankan nilai yang sama di persimpangan dua pipa.

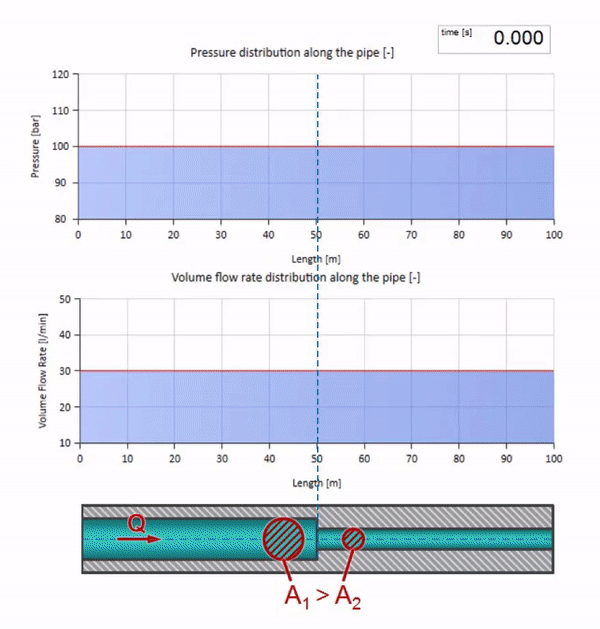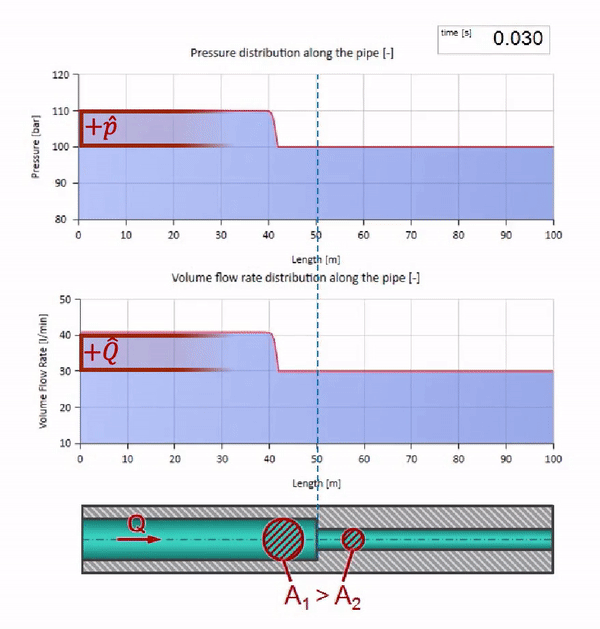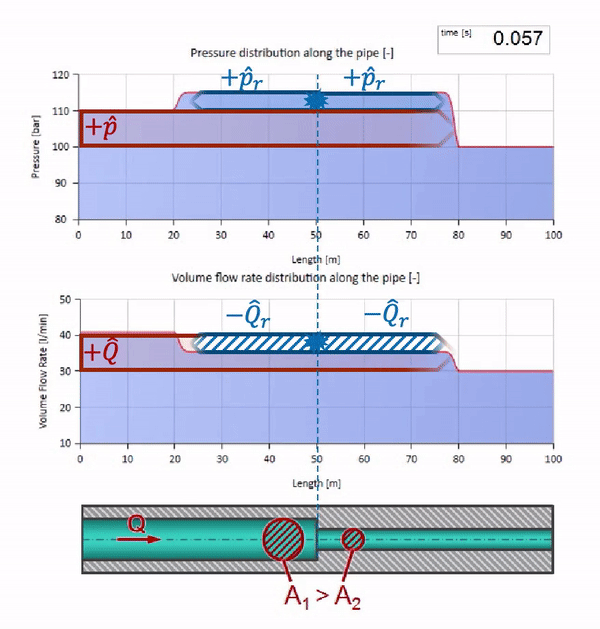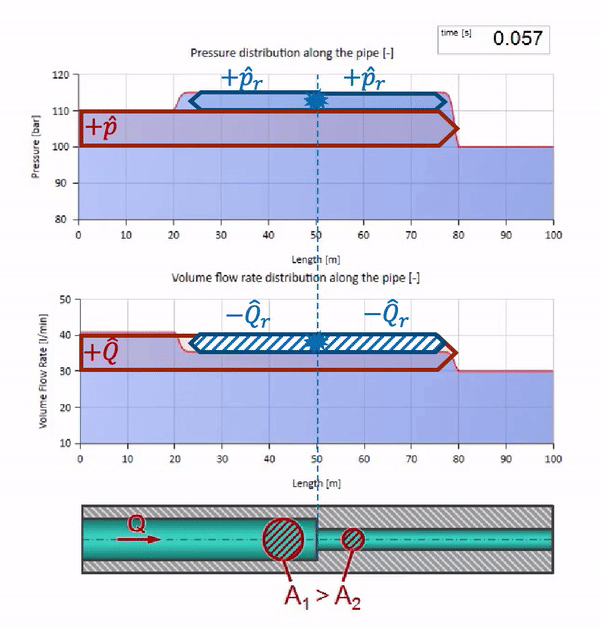
Untuk perhitungan, lebih mudah menggunakan koefisien refleksi $$$r$, yang dipertimbangkan dari impedansi gelombang dari masing-masing bagian:

$$

$$r = \ frac {Z_2-Z_1} {Z_1 + Z_2}$$

Kemudian tekanan yang dipantulkan dan gelombang aliran dapat dihitung sebagai berikut:

$$

$${\ widehat p} _r = r \; \ widehat p$$

$$

$${\ widehat Q} _r = - \ frac {\ displaystyle \; {\ widehat p} _r} {Z_1} = - r \; \ widehat Q$$

dan gelombang ini sendiri akan ditumpangkan sesuai dengan hukum gangguan dengan yang asli.
Dan itu akan terlihat seperti gambar pantulan gelombang dari situs dengan tahanan gelombang yang lebih rendah:

Dapat dilihat bahwa saat ini koefisien refleksi negatif, yang berarti bahwa gelombang tekanan setelah refleksi akan lebih sedikit, dan laju aliran, sebaliknya, lebih banyak.

Harus diingat bahwa impedansi tidak hanya bergantung pada ukuran pipa, tetapi juga pada kecepatan suara lokal. Yaitu jika kita memiliki bagian pipa dengan selongsong karet di mana kecepatan suara jauh lebih rendah, maka gelombang juga akan tercermin:

Pertama, segera menangkap mata bahwa gelombang di bagian dengan dinding karet pipa bergerak lebih lambat. Dan karena hambatan gelombang lebih rendah, maka hasil pantulan akan menyerupai kasus dengan ekspansi pipa:

Sekarang akan lebih baik untuk mempertimbangkan kasus ekstrim dengan nol dan nilai impedansi gelombang yang jauh lebih besar. Ini akan menjadi saluran keluar pipa ke tangki dengan tekanan konstan dan ujung tertutup, masing-masing. Saya akan meninggalkan animasi ini tanpa komentar:


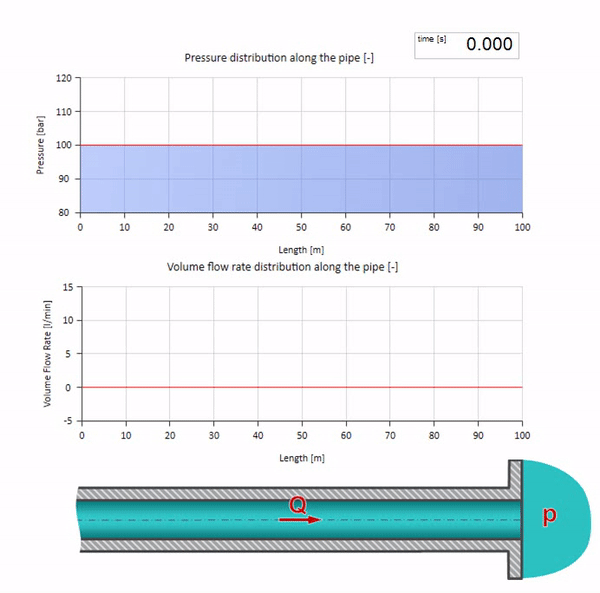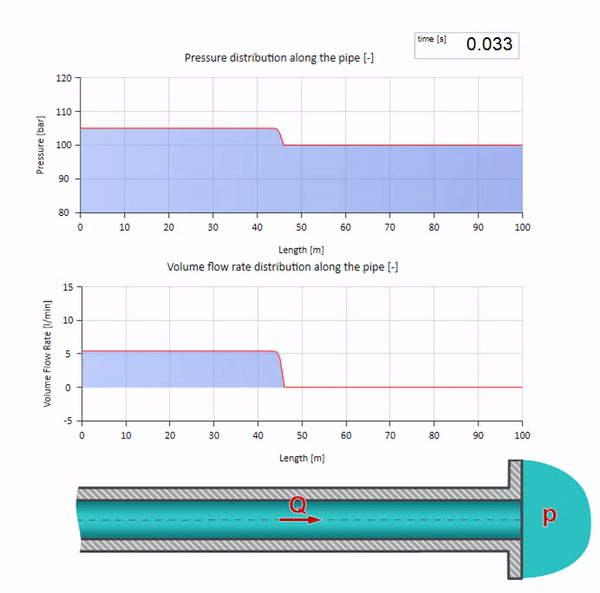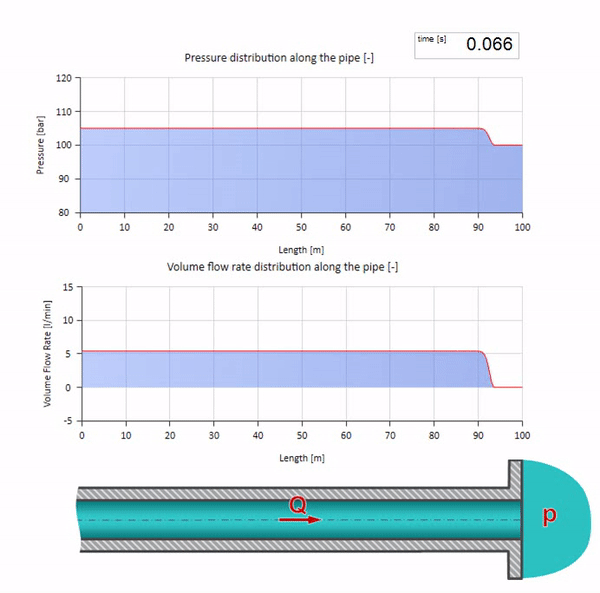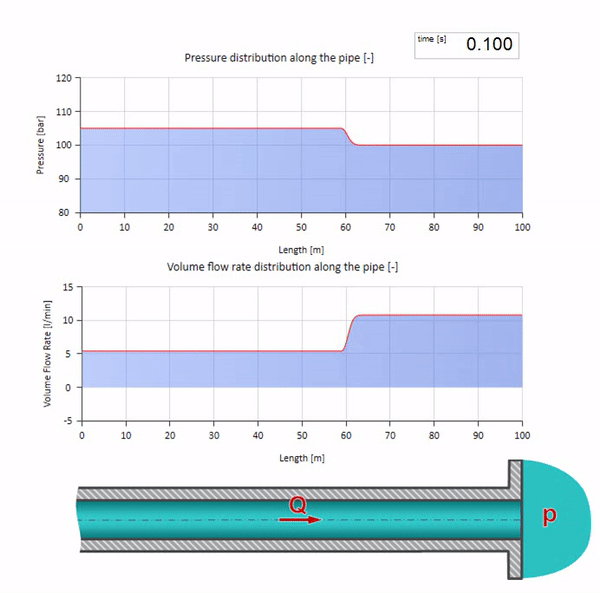
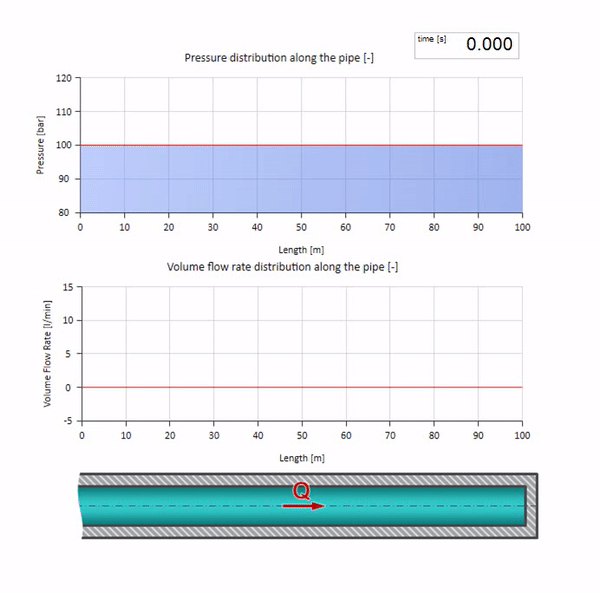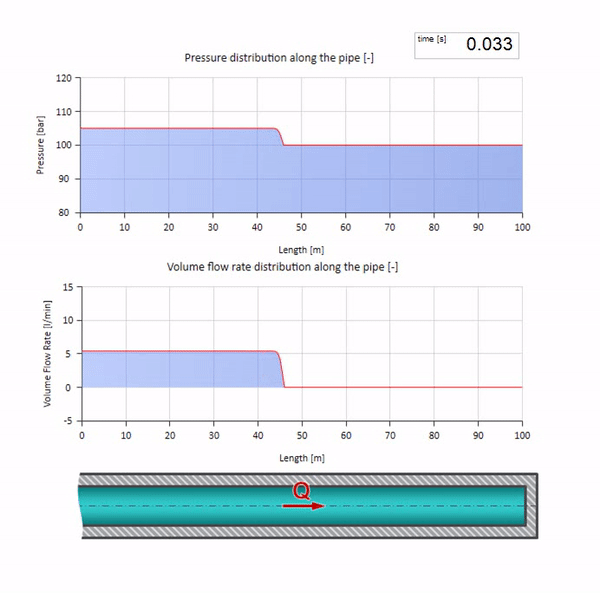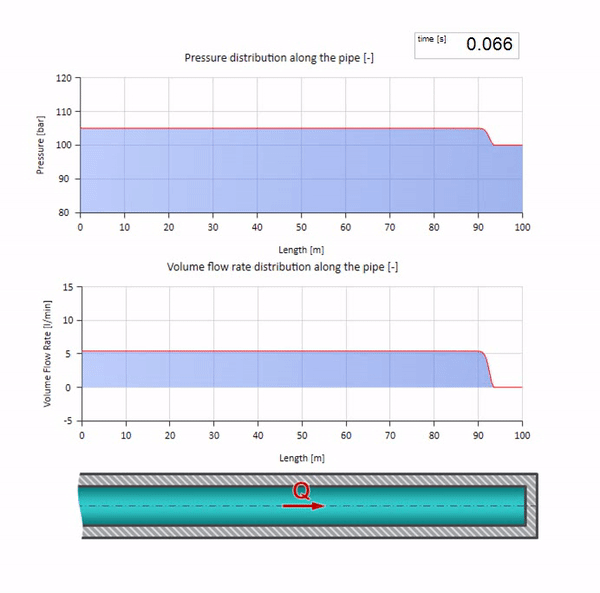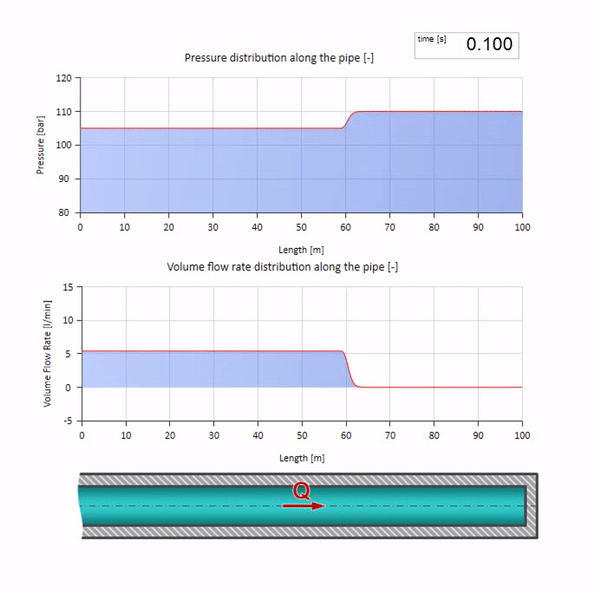
Nah, jika kita menggabungkan dua case ini, kita mendapatkan kejutan hidrolik klasik:

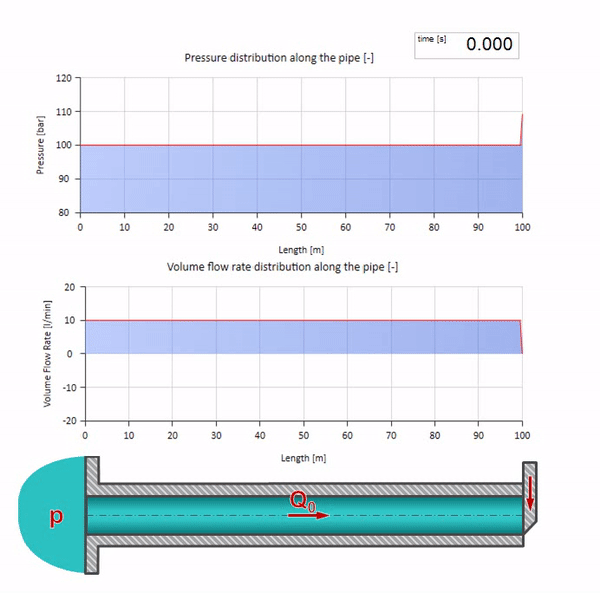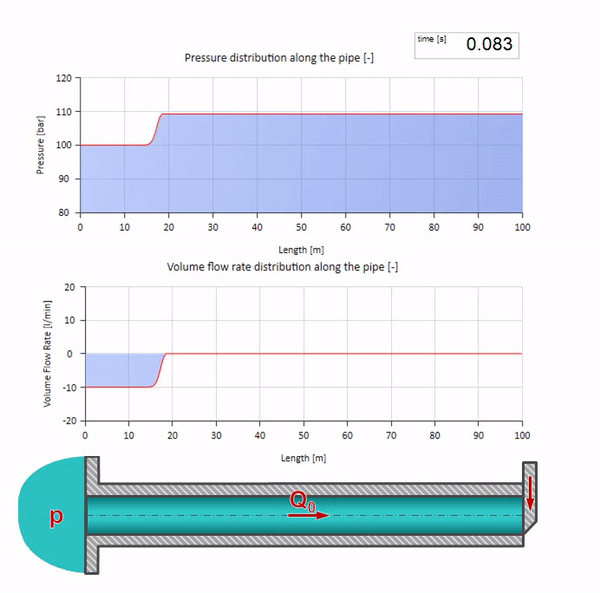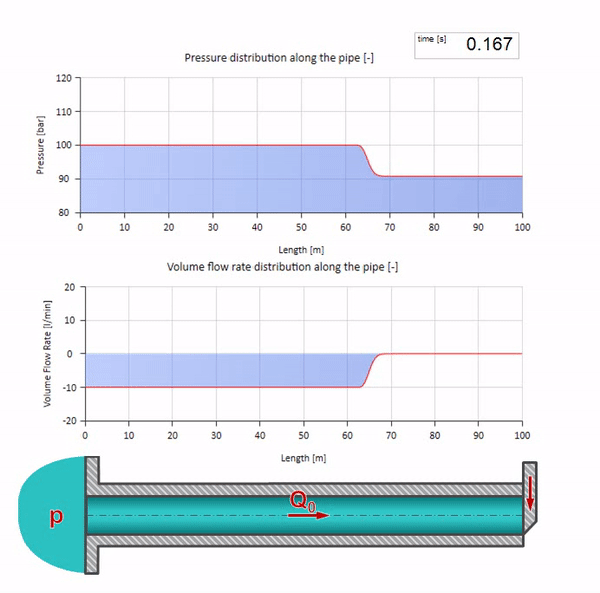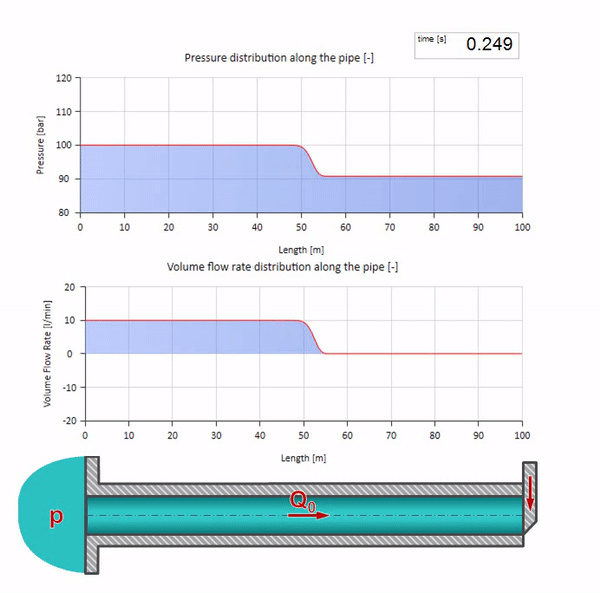
Di sini, pada saat awal waktu, ada beberapa nilai aliran yang langsung sama dengan nol di ujung kanan pipa (katup menutup). Gelombang aliran jatuh dan tekanan naik mulai bergerak ke kiri. Gelombang-gelombang ini tercermin dari ujung kanan pipa dengan impedansi nol. Dengan tidak adanya gesekan, proses ini tidak akan ada habisnya.
Menariknya, menggunakan rumus di atas, kita dapat memperoleh persamaan Zhukovsky untuk palu air:

$$

$$\ widehat p = Z_L \ widehat Q \;$$

Kami menyatakan laju aliran melalui kecepatan, dengan asumsi bahwa itu jatuh dari nilai yang diberikan ke nol, dan mengecat impedansi gelombang:

$$

$$\ widehat p = A \; v_0 \; \ frac {\ rho \; c} {\ A} = \ rho \; c \; v_0$$

Kami mendapatkan nilai lompatan tekanan yang terjadi ketika rana ditutup secara instan.

Catatan

1. Saya terinspirasi untuk menulis artikel oleh kepala buku teks dasar tentang hidrolika di Departemen Teknik Hidraulik Universitas Teknik Rhine-Westphalia di Aachen, di mana, menurut pendapat saya, proses dalam jalur hidrolik paling jelas digambarkan (Grundlagen der Fluidtechnik Teil 1: Hydraulik, Hubertus Murrenhoff ISBN: 978-3-8440 -1223-1).
2. Animasi dibuat dalam program SimulationX, perhitungan dilakukan dengan metode karakteristik