Cara membuat mekanik game yang andal di Excel. Bagian 2

Pada bagian ini, kita akan menyelesaikan masalah penempatan optimal senjata di tangki, pengaturan ruang teleporter di MMORPG dan menyeimbangkan pertempuran dari empat kelas karakter RPG.

Tugas penempatan objek

Spreadsheet untuk bagian ini dapat diunduh di sini: ( SuperTank ) ( teleporter, bagian 1 ) ( teleporter, bagian 2 )

SuperTank: masalah terpecahkan!

Pada artikel pertama seri, kami berbicara tentang contoh tugas untuk sebuah game bernama SuperTank. Pada bagian kedua, kami berkenalan dengan konsep dasar pemodelan keputusan dan saya berbicara tentang memecahkan contoh sederhana menggunakan alat "Cari Solusi" di Excel.

Sekarang kita dapat menerapkan pengetahuan yang diperoleh di bagian kedua untuk masalah SuperTank, dan membuktikan bahwa dengan bantuan mereka masalah ini dapat diselesaikan dengan mudah dan cepat. Segarkan ingatan Anda: SuperTank adalah gim di mana Anda bisa bertarung dengan tank kustom. Supertank terlihat seperti ini:


Setiap supertank dapat memiliki jumlah senjata dari lima jenis:


Supertank dapat memuat 50 ton senjata, dan seorang pemain dapat menghabiskan 100 kredit. Juga, supertank memiliki 3 "slot kritis", di mana senjata khusus seperti MegaRocket dan UltraLaser ditempatkan.

Spreadsheet untuk contoh ini dapat diunduh di sini .

Tujuannya adalah untuk mengambil senjata yang memaksimalkan kerusakan yang disebabkan oleh tangki super, tanpa melampaui batas 50 ton, 100 kredit dan 3 slot kritis. Kami juga mengasumsikan bahwa tabel ini berisi semua informasi yang diperlukan, dan bahwa faktor-faktor seperti jangkauan, frekuensi dan akurasi tidak relevan atau sudah diperhitungkan dalam parameter Kerusakan senjata yang sesuai.

Untuk mengoptimalkan skema ini, pertama-tama kita memasukkan data ini ke dalam spreadsheet. Tepat di bawahnya, kita akan menambahkan tabel lain, di mana akan ada satu set 5 "kuantitatif" sel untuk menunjukkan jumlah masing-masing dari 5 jenis senjata.

Sampai kita memasukkan nilai 1 dalam sel-sel ini, hanya untuk menguji pekerjaan mereka, tetapi ini akan menjadi sel keputusan kita - kita akan meminta alat Solver untuk menemukan nilai yang benar untuk sel-sel ini. Dimungkinkan untuk memahami bahwa ini adalah sel-sel keputusan berwarna kuning, karena kami terus mengikuti aturan pemformatan yang diuraikan di bagian kedua. Di sebelah kanan sel "kuantitatif", kami akan menambahkan sel perhitungan yang akan mengalikan nilai kuantitas dalam sel keputusan dengan nilai Kerusakan, Berat, Biaya, dan Slot Critical dari tabel di atas. Dengan demikian, setiap baris tabel ini akan menampilkan dengan benar kerusakan, berat, harga, dan slot kritis yang diperlukan untuk semua senjata yang digunakan di semua kategori senjata.


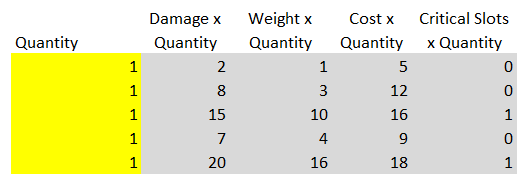
Kami juga akan membuat bagian di bawah ini, yang akan merangkum semua nilai kuantitas, berat, biaya dan slot kritis dari tabel di atas, dan membandingkan dengan nilai maksimum berat, biaya, dan slot kritis yang ditentukan dalam kondisi tugas (masing-masing 50, 100 dan 3).


Sesuai dengan aturan pemformatan dari bagian kedua artikel, sel biru di atas adalah kriteria dari kondisi masalah. Sel abu-abu adalah sel perhitungan yang mewakili berat total, biaya, dan slot kritis berdasarkan penjumlahan dari tabel kuantitas (mis., Nilai total kolom Berat x Kuantitas, Biaya x Kuantitas, dan Slot Kritis x Kuantitas). Akhirnya, sel oranye mewakili total kerusakan tangki super kami yang diterima berdasarkan kerusakan total kolom Kerusakan x Kuantitas dari tabel di atas.

Sebelum memulai, mari buat spreadsheet kami lebih ramah pengguna. Kami akan mengambil kesempatan Excel untuk menetapkan nama untuk setiap sel dan memberikan nama yang jelas ke tujuh sel dalam tabel perhitungan terakhir. Ini opsional, tetapi dalam jangka panjang itu akan membuat spreadsheet terlihat lebih jelas (misalnya, jika bukan $ F $ 21 sel akan disebut MaxCriticalSlots). Untuk melakukan ini, kita cukup memilih sel dan pergi ke bidang input nama di sebelah kiri bidang rumus, dan masukkan nama baru.


Sekarang, akhirnya, mari kita pergi ke Excel Solver dan menemukan solusinya (pergi ke sisi kanan tab Data dan pilih Solver. Jika Anda tidak melihatnya, buka Pilihan Excel , pilih kategori Add-Ins ("Add-ons"), pastikan Add-in Excel dipilih dalam daftar drop-down "Kelola", klik Go ("Go ...") dan pastikan bahwa Kotak centang Solver Add-in dipilih.

Di bidang Tetapkan Tujuan ("Optimalkan fungsi tujuan"), kami akan memilih sel oranye target, dan kemudian klik tombol radio Max ("Maksimum"). Di bidang Dengan Mengubah Sel Variabel, pilih sel keputusan (sel kuning di kolom Kuantitas tabel kedua). Di bawah, klik tombol Tambah untuk menambahkan batasan berikut:

• Nilai-nilai sel keputusan harus dalam kisaran dari 0 hingga beberapa maksimum yang masuk akal (kami memilih 50, meskipun ini mungkin nilai batas yang jauh lebih besar daripada yang diperlukan). Kita juga perlu mengatur setiap sel solusi ke batasan "= integer", karena kita tidak dapat memiliki bagian fraksional dari persenjataan, dan Excel Solver menganggap setiap variabel sebagai bilangan real secara default, kecuali jika dinyatakan sebaliknya.

• Kita juga perlu membatasi nilai total biaya, berat total, dan jumlah total slot kritis dengan nilai dari kondisi masalah. Gambar kotak dialog menunjukkan bahwa mereka sekarang memiliki nama yang nyaman yang telah kami tambahkan ke tabel bawah, yang membuat kotak dialog lebih mudah dibaca.

Sekarang kita klik pada tombol Selesaikan (“Temukan solusi”) dan setelah menunggu sebentar, Solver akan mengisi nilai-nilai Kuantitas, yang akan memberi kita yang berikut:

• 1 Senapan Mesin
• 3 roket
• 2 MegaRockets
• 1 Laser
• 1 UltraLaser

Semua ini memberi kita kerusakan total 83 unit dan membutuhkan tepat 50 ton, 100 kredit dan 3 slot kritis. Anda dapat melihat bahwa solusi terbaik tidak berubah dengan runtime Solver. Jika Anda mereset nilai-nilai ini dan melakukan optimasi kedua, atau pergi ke Opsi dan mengubah seed, maka kami akan tetap mendapatkan nilai yang sama. Kami tidak dapat 100% yakin bahwa solusi ini optimal, tetapi dengan mempertimbangkan fakta bahwa Solver tidak berhasil memperbaikinya setelah beberapa optimasi berlalu, sangat mungkin bahwa itu adalah optimal nyata, dan bukan hanya maksimum lokal.

Masalahnya terpecahkan!

Penggunaan tambahan

Hal yang keren adalah bahwa kita tidak hanya menyelesaikan masalah lebih cepat daripada yang bisa kita tangani secara manual, tetapi juga mengaturnya sedemikian rupa sehingga memungkinkan kita untuk menguji senjata mana dalam game SuperTank yang paling berguna dengan parameter yang berbeda (berat, biaya, slot kritis). Ini berarti bahwa kita relatif dapat dengan mudah mengubah efek dari berbagai perubahan dalam parameter ini pada game SuperTank, dan jika kita ingin menambahkan model tangki super alternatif baru yang akan lebih ringan, lebih berat atau memiliki jumlah slot kritis yang berbeda, maka ini dapat dilakukan dengan sangat sederhana.

Dengan mengubah semua parameter ini, kita juga dapat memperoleh pemahaman tentang kegunaan relatif dari masing-masing senjata ini, dan dengan cepat menentukan mana yang terlalu berguna, tidak cukup berguna, memiliki harga yang tidak sesuai untuk berat dan kerusakannya, dan sebagainya.

Sekali lagi, intinya adalah alat seperti itu memungkinkan kita untuk mencari ruang desain lebih cepat daripada yang kita bisa secara manual. Ini memberi kita kesempatan yang nyaman untuk mengevaluasi efek dari perubahan tersebut untuk setiap solusi desain tambahan yang dapat kita buat, apakah itu mengubah parameter senjata atau tangki super itu sendiri, menambahkan senjata baru atau model tank super, serta menambahkan parameter baru (misalkan batas ukuran adalah dalam meter kubik).

Untuk memahami apa yang saya maksud, buka sel biru "Biaya Maks." Dan ubah nilainya dari 100 menjadi 99. Sekarang jalankan Solver lagi dan Anda akan mendapatkan tata letak senjata yang sama sekali berbeda:

• 0 Senapan Mesin
• 2 roket
• 3 MegaRockets
• 3 laser
• 0 UltraLaser

Skema semacam itu memberikan indeks kerusakan yang sedikit lebih rendah (82 bukannya 83), tetapi secara radikal berbeda dari yang sebelumnya.

Jika Anda menetapkan nilai Biaya Maks ke 101 atau 102, dan melakukan perhitungan lagi, maka ada kemungkinan bahwa kami akan mendapatkan konfigurasi yang mirip dengan yang pertama atau bersamaan dengan itu; Meskipun demikian, kerusakan akan tetap sama dengan 83 (skema dapat berubah, karena dalam kasus seperti itu ada beberapa skema optimal). Namun, jika Anda menetapkan Biaya Maks ke 103, Anda harus mendapatkan yang berikut ini:

• 1 Senapan Mesin
• 4 roket
• 2 MegaRockets
• 0 laser
• 1 UltraLaser

Yang meningkatkan total kerusakan menjadi 84.

Ini menarik: susunan senjata ini sangat berbeda dari dua yang pertama.


Seperti yang Anda lihat, kami mendapatkan hasil yang tidak terduga: pilihan senjata yang optimal dalam skema kami sangat tergantung pada parameter tangki super dan dapat bervariasi secara signifikan bahkan dengan perubahan kecil pada parameter ini. Selain itu, itu memberi kita segala macam informasi yang berguna: semua lima jenis senjata berguna dalam setidaknya dua dari tiga pengaturan tangki super, dan Rockets dan MegaRockets jelas berguna dalam ketiganya. Tampaknya ini memberitahu kita bahwa kelima jenis senjata seimbang, yaitu, berguna relatif satu sama lain, dan pada saat yang sama mereka tetap unik.

Dan seperti yang dapat Anda perhatikan, pemodelan dan optimalisasi solusi seperti itu memberi kami peluang yang sangat baik untuk melakukan pencarian dengan cepat di lingkungan lokal dan mengoptimalkan kembali. Untuk beberapa jenis tugas, ini akan memungkinkan kami untuk mendeteksi strategi dominan dan eksploitasi pemain yang sulit atau tidak mungkin ditemukan dengan cara lain.

Teleports - Wormhole

Melihat dua contoh terakhir (contoh tarif pajak dalam permainan strategis dan SuperTank), Anda mungkin berpikir bahwa teknik seperti itu hanya berlaku dalam kasus di mana pengguna berurusan dengan angka. Tetapi Anda akan benar-benar salah! Seperti yang akan kita lihat, ada banyak contoh bagaimana Anda bisa mendapatkan manfaat dari mengoptimalkan elemen desain yang tidak hanya tidak terlihat seperti angka bagi pengguna, tetapi tidak terlihat sama sekali!

Anda juga mungkin berpikir bahwa pemodelan keputusan hanya berlaku untuk keputusan yang dapat dibuat pemain dalam permainan. Ini juga tidak benar: dalam beberapa kasus mereka dapat digunakan untuk pemodelan untuk mengoptimalkan solusi Anda sendiri sebagai seorang desainer.

Misalkan Anda sedang mengerjakan MMORPG ruang. Suatu hari, desainer utama Anda mendatangi Anda dengan kecemasan yang terlihat di wajahnya. "Kami sedang menyelesaikan desain ulang sektor Omega," katanya. “Dan kami punya masalah. Kami berencana untuk menambahkan beberapa teleporter lubang cacing "di segmen dunia ini, tetapi kami tidak bisa sepakat di mana menempatkan mereka."

"Berapa banyak teleporter?" Anda bertanya.

“Kami belum tahu. Mungkin tiga, tetapi bisa dari dua hingga empat. Kami belum yakin. " Lalu dia menunjukkan Anda peta yang terlihat seperti ini:


"Apa ini?" Anda bertanya.

“Ini adalah peta sektor Omega. Atau setidaknya sistem bintang yang dapat dikunjungi pemain di kuadran ini. Kita perlu menentukan di sel mana seharusnya lubang cacing itu berada. ”

“Baiklah, dan dengan aturan apa mereka ditempatkan? Mungkinkah menempatkan lubang cacing di satu kuadran dengan sistem bintang? "

"Kami ingin Anda menempatkan lubang cacing sedemikian rupa untuk meminimalkan jarak dari sistem bintang mana pun ke lubang cacing terdekat. Dan ya, Anda bisa menempatkan mereka di kuadran yang sama dengan sistem bintang; mereka hanyalah teleporter kecil yang tergantung di ruang angkasa, sehingga mereka dapat ditempatkan di mana saja. Dan ingat bahwa kita belum memutuskan berapa banyak yang harus ada, jadi beri saya solusi untuk 2, 3, dan 4 lubang cacing. "

Bagaimana merumuskan masalah ini, dan bagaimana menyelesaikannya?

Mengoptimalkan teleporter!

Mari kita mulai dengan menyiapkan sel-sel solusi. Kami menyatakan empat teleport sebagai A, B, C dan D. Kami tahu bahwa setiap teleport pada dasarnya tidak lebih dari koordinat (x, y) pada peta bintang sektor Omega. Kami juga tahu bahwa kami akan memerlukan beberapa cara untuk menunjukkan jumlah teleport aktif, jadi kami akan menambahkan sel yang memungkinkan Anda untuk mengatur jumlah teleport. Kami hanya menggunakan teleport D ketika 4 lubang cacing digunakan, dan C hanya ketika kami memiliki 3 atau lebih.


Di bawah ini kami akan menyiapkan tabel untuk menghitung jarak dari setiap sistem bintang ke teleport terdekat. Tabel ini terlihat seperti ini:


Biru kiri menunjukkan koordinat dari setiap sistem bintang pada peta. Setiap baris adalah satu sistem bintang. Kami hanya memindahkannya dari peta sektor Omega, yang diberikan kepada kami oleh desainer terkemuka.

Di sebelah kanan, kami menghitung jarak ke masing-masing dari empat teleporter. Ini hanya teorema Pythagoras. Jarak dihitung sebagai akar kuadrat dari jarak horizontal dan vertikal antara sistem bintang dan teleportasi:

= SQRT (($ B14-Axe) ^ 2 + ($ C14-Ay) ^ 2)

(Jangan khawatir - saya berjanji bahwa ini adalah matematika paling sulit yang akan kita temui dalam seri!)

Kami mengambil koordinat X dan Y dari setiap sistem bintang dari sel-sel biru dari tabel di atas, dan koordinat X dan Y dari setiap teleportasi (sel dengan nama Ax dan Ay untuk teleport A dalam fungsi SQRT () yang ditunjukkan di atas) dari sel-sel larutan kuning di bagian atas.

Akhirnya, kami mengambil minimum dari empat nilai ini di kolom Dist to Closest, yaitu, kami cukup menggunakan fungsi MIN () untuk menentukan minimum empat nilai di sebelah kiri. Lalu kami merangkum seluruh kolom di bawah ini; jumlahnya adalah sel target.

Anda mungkin telah memperhatikan bahwa dalam tangkapan layar di atas semua sel diatur ke Dist ke D. Alasannya adalah bahwa kita menggunakan "Jumlah Teleporter?" Cell di bagian atas model solusi, yang memungkinkan Anda mengonfigurasi jumlah teleport yang diperhitungkan. Jika jumlah teleporter adalah 2, maka kita menggunakan nilai 99 baik di Dist ke C dan Dist ke D, dan jika itu adalah 3, maka nilai 99 hanya digunakan di kolom Dist to D. Karena itu, setiap sistem bintang akan mengabaikan semua teleporter yang tidak perlu saat menghitung jarak ke teleport terdekat dalam kasus 2 atau 3 teleport.

Sekarang kita akan meluncurkan Solver:


Sel target adalah jumlah di bagian bawah kolom Dist to Closest. Perhatikan bahwa tidak seperti contoh lainnya, di sini kami ingin menggunakan tombol radio "To: Min" karena kami membutuhkan jarak minimum antara semua sistem bintang dan teleporter, bukan maksimum.

Di bawah ini, kami akan menunjukkan delapan sel kuning untuk menyelesaikan koordinat X dan Y dari lubang cacing A, B, C, dan D sebagai sel dari solusi (Dengan Mengubah Variabel Sel). Pada bagian pembatasan, kami akan membatasi masing-masing koordinat sebagai nilai integer dalam kisaran dari 0 hingga 12. Perhatikan bahwa kami menggunakan batasan integer untuk sel-sel solusi ini, karena kami maksudkan bahwa perancang utama hanya ingin tahu sel mana yang akan diteleportasi, tetapi kami dapat dengan mudah melewati batasan ini jika perancang membutuhkan koordinat bahan.

Jika kita meminta "Jumlah Teleporter?" nilai 2, 3 dan 4, dan secara berurutan kita akan meluncurkan Solver pada setiap nilai, kita akan mendapatkan konfigurasi berikut:


Dengan informasi ini, kita dapat mendekati perancang terkemuka dan menunjukkan kepadanya lokasi optimal untuk lokasi sejumlah teleporter dalam rentang 2 hingga 4. Ini adalah bagaimana lokasi optimal "lubang cacing" untuk 2, 3 dan 4 teleportasi terlihat pada peta (ditunjukkan dengan warna hijau).


Spreadsheet untuk contoh ini dapat diunduh dari sini .

Apakah saya berbicara tentang ninja?

"Luar biasa," kata perancang utama, tetapi Anda melihat penderitaan di wajahnya. “Eh, tapi aku lupa memberitahumu bahwa beberapa sistem ini dihuni oleh ninja luar angkasa. Dan kami ingin sistem dengan ninja berada jauh dari "lubang cacing" sehingga para pemain tidak merasakan ancaman yang berlebihan. "

"Wow. Ini benar-benar mengubah kasusnya. "

"Benar. Selain itu, dalam beberapa sistem bintang tidak ada satu tetapi dua koloni, yaitu, mereka dua kali lebih penting daripada yang dekat dengan teleporter. Atau dua kali lebih penting untuk lebih jauh jika itu adalah sistem dengan dua koloni ninja ruang angkasa. Seperti apa peta ini sekarang: "


Dia melanjutkan: “Setiap angka negatif adalah koloni ninja ruang angkasa. Sistem dengan angka 2 berisi dua koloni manusia, dan dengan angka -2 mengandung dua koloni ninja. Bisakah Anda memberi tahu saya di mana harus menempatkan teleporter dalam kasus ini? "

"Katakan padaku, setidaknya kamu sudah memutuskan berapa banyak bank yang akan ada: 2, 3 atau 4?", Kamu bertanya dengan sinis.

"Aku takut belum."

Kami menyelesaikan dengan mempertimbangkan ninja

Untuk mengatasi masalah ini, kita perlu menambahkan kolom baru ke tabel yang menunjukkan berat tabel. Kami akan menyebutnya "pengganda". Kami hanya akan mengalikan nilai ini dengan nilai di kolom Dist to Closest.

Ketika kita melakukan ini, Dist to Closest sedikit mengubah artinya. Sekarang ini bukan jarak ke sistem bintang terdekat, karena untuk sistem bintang ninja nilainya berubah -1 kali. Itu menyerupai "poin" yang lebih umum (skor), jadi mari kita sebut itu.


Dengan demikian, poin sekarang menunjukkan nilai kumulatif. Dengan meminimalisirnya, kami membuat Solver berusaha sedekat mungkin dengan sistem dengan koloni manusia sebanyak mungkin dan pada saat yang sama sejauh mungkin dari sistem ninja yang padat.

Sekarang kita mendapatkan hasil berikut:


Seperti yang Anda lihat, ini memberi kita konfigurasi teleporter, dalam setiap kasus sangat berbeda dari versi yang lebih sederhana tanpa ninja.


Spreadsheet untuk versi contoh teleport yang diperluas ini dapat diunduh dari sini .

Seperti yang Anda lihat, model solusi kami dapat dengan cepat menyelesaikan tugas non-sepele ini, dan kami dapat menyesuaikannya dengan perubahan persyaratan.

Tugas ini termasuk dalam kelas tugas yang disebut "tugas alokasi objek", yang dipelajari dengan sangat baik di bidang manajemen operasional. Tapi seperti yang Anda lihat, mereka berpotensi digunakan dalam desain game, serta dalam desain level, dan solusinya sederhana (jika tidak sepele) di Excel.

Player-vs-Player

:

Dalam tiga bagian sebelumnya dari seri artikel ini, kami memperkenalkan diri pada konsep pemodelan dan optimalisasi solusi, serta alat "Solver" dari paket Excel. Kami menunjukkan bagaimana mereka dapat digunakan untuk menghitung tarif pajak optimal kota dalam strategi 4X, untuk menentukan penempatan teleporter yang optimal dalam permainan luar angkasa, dan untuk memilih tata letak senjata yang optimal untuk tugas tangki super yang dijelaskan di bagian pertama.

Sebuah pertanyaan alami muncul: bagaimana dengan menyeimbangkan permainan? Apakah mungkin untuk menerapkan teknik serupa pada semua jenis tugas penyeimbangan kompleks yang ditemukan di berbagai jenis permainan, khususnya, dalam strategi, RPG dan MMORPG?

Jawaban untuk pertanyaan ini adalah ya, tentu saja, tetapi dengan banyak reservasi. Spreadsheet khususnya memiliki banyak keterbatasan, karena dalam kebanyakan kasus non-sepele mereka tidak secara akurat menggambarkan permainan. Oleh karena itu, akan sulit bagi kami untuk melakukan penyeimbangan yang andal menggunakan teknik optimisasi; tugas menyeimbangkan nyata dari sebagian besar game akan jauh melampaui apa yang bisa kita modelkan dalam spreadsheet. Simulasi permainan itu sendiri biasanya terlalu rumit, memiliki banyak "bagian yang bergerak" dan sering dilakukan secara real time, ketika mencoba untuk simulasi diskrit, kita dapat menghadapi semua jenis masalah.

Karena itu, jika kita ingin menggunakan teknik serupa untuk menyeimbangkan kelas di MMORPG seperti WildStar atau dalam game strategis sepertiPenghancuran Planetary , maka untuk memastikan setidaknya beberapa keakuratan dan kegunaan, kita harus mengintegrasikannya ke dalam simulasi permainan itu sendiri.

Selain itu, kebenarannya adalah bahwa beberapa aspek keseimbangan tidak dapat otomatis; seperti yang kami jelaskan di bagian pertama artikel, tidak mungkin menyesuaikan pengalaman game secara otomatis.

Oleh karena itu, yang terbaik yang bisa kita harapkan adalah demonstrasi contoh sederhana yang menggambarkan pendekatan umum untuk tugas-tugas jenis ini: dengan contoh sederhana di Excel, kita akan belajar cara mendekati perumusan masalah keseimbangan jenis ini dan mengoptimalkannya. Kami akan menunjukkan bahwa, setidaknya untuk contoh pertempuran sederhana, Solver dapat dengan baik menyeimbangkan beberapa kelas RPG satu sama lain. Kemudian Anda dapat menggunakan struktur dasar ini sebagai dasar untuk menyelesaikan masalah optimisasi seperti itu dengan skema yang lebih kompleks dan lebih terintegrasi ke dalam simulasi permainan.

Kami berharap bahwa bersama kami Anda akan mempelajari semua trik dan melihat apa yang dapat diberikan contoh sederhana ini kepada kami.

Tidak seimbang

Tidak ada definisi tunggal, yang diterima secara umum dari kata “balancing”. Ini memiliki banyak arti, dan benar biasanya tergantung pada konteks permainan yang dimaksud. Dalam kondisi yang berbeda, penyeimbangan dapat dikaitkan dengan menyiapkan beberapa kelas karakter untuk menyamakan kemampuan mereka dalam permainan permainan peran, dengan jumlah kekuatan lawan yang saling bertarung dalam permainan strategis, atau dengan menyesuaikan biaya berbagai unit atau sumber daya sesuai dengan kegunaannya.

Definisi “penyeimbangan” terbaik biasanya tergantung pada tujuan desain gim yang bersangkutan, tetapi karena tujuan ini dapat berupa apa saja, tidak mungkin untuk menentukan apriori apa arti penyeimbangan sebenarnya untuk gim pada umumnya.

Beberapa pemain cenderung percaya bahwa menyeimbangkan dalam pertempuran berarti kerusakan yang sama. Hal ini terutama berlaku untuk MMORPG, di mana pemain sering mengeluh bahwa kerusakan per detik (DPS) satu kelas terlalu kecil atau terlalu besar relatif terhadap yang lain.

Tentu saja, kelas tidak dapat diseimbangkan hanya dengan DPS; dapat diterima bahwa satu kelas memiliki DPS lebih besar dari yang lain, tetapi ini harus diimbangi oleh faktor-faktor lain yang membatasi kegunaan keseluruhan kelas, misalnya, mengurangi kelangsungan hidup atau DPS jangka panjang lebih sedikit dibandingkan dengan DPS jangka pendek.

MMO kecil

Bayangkan kita sedang membuat proyek baru, permainan peran-peran online multipemain massively yang sangat disederhanakan yang disebut "Tiny MMO". Sebagai bagian dari pengembangan desain, kami berusaha untuk menyeimbangkan empat kelas untuk pertarungan pemain-ke-pemain (PVP) sehingga keempat kelas relatif sama dalam pertempuran satu sama lain, dan bahwa tidak ada kelas "lebih baik" atau "lebih buruk" yang jelas. Anda bisa bertarung melawan kelas lain.

Meskipun Tiny MMO adalah gim real-time, setiap aksi pemain berlangsung tepat 3 detik, jadi kami dapat mendiskritkannya dengan menghadirkannya sebagai gim berbasis giliran di mana setiap gerakan merupakan bagian dari gameplay tiga detik.

Pemain dalam game ini dapat memilih satu dari empat kelas karakter:

• Prajurit melakukan kerusakan paling besar.
• Mage melemparkan mantra dari kejauhan dan memiliki jangkauan serangan terpanjang dari keempat kelas
• Penyembuh (Healer) secara otomatis dirawat, memulihkan untuk setiap giliran bagian tertentu dari kesehatannya
• Barbar (Barbar) memiliki kesehatan terbanyak

Ini semua yang kita ketahui tentang empat kelas ini, dan kita perlu mengatur parameter awal kesehatan (HP), kerusakan, penyembuhan dan berbagai serangan untuk keempat kelas. Kita perlu menyeimbangkannya sedemikian rupa sehingga masing-masing kelas unik dan karakteristiknya berbeda secara signifikan dari semua kelas lainnya, tetapi sebagai hasilnya masing-masing kelas ternyata menjadi "seimbang" mungkin sehubungan dengan tiga lainnya.

Dengan kata lain, kami berusaha untuk mengoptimalkan tabel berikut:


Sementara kami menggunakan nilai sementara dan menganggap bahwa setiap kelas dimulai dengan 50 HP, memberikan 10 kerusakan per putaran, menyembuhkan 0 HP per putaran dan memiliki jangkauan serangan 40 meter. Setiap karakter bergerak dengan kecepatan 10 meter per putaran. Karena desain menunjukkan bahwa keempat kelas karakter dapat bergerak pada kecepatan yang sama, kami akan mempertimbangkan nilai ini konstan, dan kami tidak akan memasukkan kecepatan gerakan ke dalam tabel variabel keputusan.

Jelas, ini adalah studi kasus dengan model kerusakan yang sangat sederhana. Ini adalah nilai rata-rata kerusakan yang berkelanjutan per detik, yang mengabaikan perbedaan antara kerusakan impuls dan kerusakan jangka panjang, serta mana dan mekanika lain yang memodifikasi kemampuan serangan kelas. Kami hanya akan memiliki satu jenis kerusakan, yang cukup tidak realistis, karena sebagian besar kelas memiliki puluhan jenis kerusakan, dan kami perlu menerapkan sistem AI yang memilih serangan di setiap belokan. Selain itu, di sebagian besar permainan, kerusakan memiliki unsur keacakan, tetapi untuk sekarang kita akan menghilangkan ini dan menganggap bahwa variabilitas kerusakan tidak begitu besar sehingga secara signifikan mempengaruhi hasil pertempuran antara kedua kelas.

Tentu saja, keseimbangan apa pun yang dilakukan di Excel tidak mungkin ideal atau konsisten dengan saldo akhir permainan; dia harus melalui banyak iterasi playtesting. Tetapi jika kita mengambil satu atau dua jam untuk mendapatkan opsi pertama yang bagus untuk game kita di Excel, maka setidaknya kita lebih cenderung mendekati parameter kualitatif saldo awal, yang akan membawa kita lebih dekat ke saldo akhir yang ingin kita dapatkan.

Meja kemenangan

Kita perlu menyeimbangkan empat kelas satu sama lain dalam pertempuran satu lawan satu. Karena kita hanya memiliki 4 kelas (Warrior, Mage, Healer, dan Barbarian), ada 6 kemungkinan kombinasi kelas yang berbeda:

• Warrior - Mage
• Warrior - Healer
• Warrior - Barbarian
• Mage - Penyembuh
• Mage - Barbar
• Tabib - Barbar

Penyeimbangan ini bisa sangat rumit. Bahkan dalam kasus kami yang sederhana dengan empat kelas, kami mendapat enam hubungan antar kelas, sama seperti kita bisa menggambar enam garis antara empat titik persegi.


Setiap kali kita ingin membuat bahkan perubahan kecil di salah satu parameter dari salah satu kelas, perubahan ini juga akan mempengaruhi PvP keseimbangan antara pasangan ini kelas, dan yang lainnya dua kelas. Keterkaitan kekuatan-hukum ini hanya akan tumbuh dengan peningkatan jumlah kelas, dan keputusan tentang menyeimbangkan PvP antara setiap pasangan kelas yang dibuat "dalam ruang hampa", tanpa memperhitungkan semua interaksi lainnya, dapat menjadi sangat berbahaya.

Idealnya, kami ingin membuat semacam tabel kemenanganseperti yang ditunjukkan di bawah ini. Jika kita dapat mensimulasikan pertempuran antara masing-masing 6 pasangan ini dalam spreadsheet, maka kita akan dapat menghasilkan variabel "poin" tertentu untuk masing-masing dari 6 pasangan. Semakin banyak poin, semakin baik, sehingga kita dapat menggabungkan keenam poin ini untuk menghasilkan fungsi tujuan.


Perhatikan bahwa dalam tabel di atas, sel-sel di sepanjang diagonal adalah nol, karena mereka menunjukkan pasangan dari kelas yang sama yang akan seimbang dengan definisi. Selain itu, sel-sel di sudut kanan atas juga nol, karena mereka menunjukkan pasangan yang persis sama dengan sel-sel di kiri bawah.

Sekarang mari kita siapkan model untuk pertempuran antara dua kelas yang berbeda.

"Simulator pertempuran"

Kami akan mengatur setiap pasangan kelas pada jarak 100 meter dari satu sama lain. Setiap karakter memiliki 3 detik untuk diserang, sehingga kita dapat membayangkan ini sebagai simulasi berbasis giliran di mana setiap "bergerak" berarti 3 detik. Pada setiap "bergerak", masing-masing karakter menyerang yang lain, jika ia berada dalam jangkauan serangan, atau terus bergerak untuk mengurangi jarak.

Simulasi terlihat seperti ini:


Di atas adalah sepasang karakter yang memasuki pertempuran: dalam hal ini, Mage (kelas 1) dan Penyembuh (kelas 2). Kolom kiri menunjukkan jarak saat ini antara dua karakter yang disimulasikan.

Untuk setiap karakter, kolomnya adalah:

• Max Range : , . .
• Healing : , .
• HP : . HP , . , .
• Damage : , , . , 0.
• Serangan? : Kolom ini memeriksa apakah karakternya dalam jangkauan serangan. Jika demikian, ini berarti bahwa karakter menyerang pada giliran saat ini; jika tidak, karakter bergerak lebih dekat untuk mencapai karakter lain.

Dengan demikian, kedua karakter mulai bergerak ke arah satu sama lain, dan kemudian menyerang sampai salah satu atau keduanya mati. Setiap karakter bergerak setiap 3 detik 5 meter (5 meter per "putaran"). Ketika kedua karakter bergerak ke arah satu sama lain, Range akan berubah di setiap belokan sebanyak 10 unit, dan sebanyak 5 unit jika hanya satu dari mereka yang bergerak. Permainan itu sendiri terstruktur sehingga kedua karakter dapat mulai bergerak secara bersamaan, setelah itu gerakan diperbolehkan pada saat yang sama, sehingga ada kemungkinan bahwa kedua karakter dapat mati pada saat yang sama.

Selanjutnya, kita perlu mengatur skor untuk tabel ini dan menghasilkan nilai numerik yang menunjukkan seberapa bagus pertempuran itu; dengan kata lain, seberapa dekat kita dalam mencapai tujuan desain kita.

Jelas, kami ingin kedua karakter mati pada akhir pertempuran, atau setidaknya sedekat mungkin dengan kematian. Jika pertempuran seimbang, maka kedua kelas pertempuran harus meminimalkan kesehatan musuh di akhir pertempuran.

Namun, ini saja tidak cukup. Jika kita mengatur skor dengan cara ini, maka optimizer hanya akan memaksimalkan nilai kerusakan sehingga kedua karakter langsung saling membunuh! (Jika Anda penasaran, coba ubah spreadsheet yang terlampir pada artikel untuk dilihat sendiri.) Jelas, kami tidak bertujuan untuk kematian instan: kami membutuhkan kedua karakter mati atau hampir mati pada akhir pertempuran, tetapi pada saat yang sama kami ingin pertarungan bertahan dalam jumlah waktu yang wajar.

Dengan kata lain, kami tidak hanya berusaha untuk memastikan keseimbangan semua kelas yang relatif sama terhadap satu sama lain; kami juga ingin membuat keseimbangan menarik , termasuk pertarungan yang berlangsung dalam waktu yang sesuai.

Untuk menghasilkan estimasi keseimbangan seperti itu, kita perlu membuat beberapa sel di sebelah kanan setiap tabel. Durasi menunjukkan durasi pertempuran; dia menghitung jumlah baris dalam tabel di mana kedua karakter masih hidup. Total HP menghitung total poin hit dari dua karakter yang masih hidup. Idealnya, harus 0, yaitu, pada saat pertempuran berakhir, kedua karakter sedang sekarat.


Dan akhirnya, Skor menggabungkan durasi dan jumlah total poin hit dalam formulir (Durasi / (1 + Total HP)). Perhatikan bahwa kami menambahkan 1 ke pembagi, karena Total HP bisa 0, dan dalam hal ini kami akan mendapatkan pembagian dengan kesalahan nol. Dengan demikian, kami dapat menjamin bahwa kami menghargai pengoptimal untuk menemukan durasi maksimum pertempuran dan nilai minimum dari jumlah poin hit.

(Perhatikan bahwa karena kita memiliki 17 baris dalam setiap "simulasi" pertempuran kelas ke kelas. Ini berarti bahwa kita pada dasarnya membuat keputusan desain bahwa pertarungan harus berlangsung sekitar 17 putaran. Jika kita ingin pertarungan menjadi lebih pendek atau lebih lama, Anda dapat mengubah jumlah baris, mengedit rumus untuk menghitung skor, dan melakukan pengoptimalan kedua yang sesuai.)

Akhirnya, kami mengambil keenam nilai Skor ini (satu untuk setiap tabel) dan menggunakannya di Tabel Kemenangan di atas untuk menunjukkan hasil pertempuran antara setiap pasangan kelas.

Anda bisa meringkas keenam nilai skor ini dan menggunakan hasilnya sebagai nilai Skor akhir. Namun, jika kita melakukan ini, maka Solver kemungkinan besar tidak akan dapat menemukan keseimbangan yang baik antara peringkat tertinggi dan terendah untuk pertarungan individu, dan juga akan menerima peringkat yang sangat tinggi untuk beberapa pasangan kelas dan peringkat rendah untuk yang lain. Ini bukan yang kita inginkan: kita membutuhkan semua tanda untuk menjadi tinggi dan kita berusaha untuk menaikkan semuanya. Untuk memperbaikinya, kita mengalikan jumlah nilai dengan nilai terkecil dalam grup (menggunakan fungsi Excel MIN ()) untuk membuat Solver fokus pada nilai dengan nilai terendah.

Tambahkan batasan

Kami belum selesai. Jika Anda mengoptimalkan model solusi dengan parameter saat ini, maka kemungkinan besar kelas tidak akan dikonfigurasi dengan benar - pada kenyataannya, sangat mungkin bahwa model akan menulis nilai HP, Damage, Healing, dan Range yang sama ke tabel variabel keputusan.

Dan kami, tentu saja, ingin setiap kelas memiliki kepribadiannya sendiri. Kami membutuhkan Warrior untuk melakukan kerusakan paling besar, Mage memiliki Range terbesar, Healer memiliki nilai Healing maksimum, dan Barbarian memiliki HP tertinggi. Kami juga ingin perbedaan-perbedaan ini tidak terlalu kecil - kami perlu kelas-kelas ini menjadi sangat berbeda satu sama lain.

Untuk melakukan ini, kami akan membuat tabel kecil pembatasan. Tabel ini memastikan bahwa masing-masing dari empat kelas akan memiliki atribut yang sesuai, dan kemudian memberikan skor 0 atau 1, tergantung pada apakah kondisi kendala terpenuhi.


Perbedaan tabel Min di sebelah kanan menunjukkan perbedaan minimum dari setiap atribut kelas relatif terhadap semua kelas lainnya. Dengan kata lain, Warrior harus memiliki setidaknya 4 kerusakan HP lebih dari semua kelas lain, Mage harus memiliki jangkauan serangan minimal 10 lebih, dan seterusnya.

Sekarang kami telah menambahkan batasan khusus ini, sekarang saatnya untuk mengoptimalkan!

Cari solusi

Sekarang kita dapat menjalankan alat Solver ("Finding Solutions") yang dibangun dalam Excel untuk mencoba mengoptimalkan parameter awal. Sebagai sel target, kami akan memilih sel Skor, yang menggabungkan hasil dari semua enam turnamen. Kami menetapkan variabel keputusan untuk memasukkan semua 16 sel dalam tabel variabel Keputusan kuning yang kami buat di awal.

Kami juga menetapkan batasan (di bidang Subjek ke Kendala) sebagai berikut:

• Semua sel keputusan harus bilangan bulat dengan nilai minimum 0.
• Semua sel dalam kolom HP harus memiliki nilai maksimum 200 dan minimal 30.
• Semua sel di kolom Kerusakan memiliki nilai maksimum 20.
• Semua sel di kolom Penyembuhan memiliki nilai maksimum 15.
• Semua sel di kolom Rentang memiliki nilai maksimum 100.
• Selain itu, keempat sel di bagian Kendala khusus harus diatur ke 1 untuk memenuhi kondisi khusus mereka.

Terakhir, atur Metode Solving ke Evolutionary dan jalankan Solver. Harap dicatat bahwa karena ini adalah algoritma evolusioner, ada kemungkinan untuk meningkatkan solusi yang ditemukan selama menjalankan Solver kedua atau ketiga, atau setelah mengatur parameter (tombol Pilihan) untuk optimasi evolusioner.

Akibatnya, kita harus mendapatkan sesuatu yang serupa:


... dan seolah-olah secara ajaib, Solver memberi kami konfigurasi keseimbangan awal yang baik.

Seperti yang Anda lihat, Warrior sekarang melakukan kerusakan paling besar, Mage memiliki jangkauan terbesar, Healer menyembuhkan terbaik, dan Barbarian memiliki HP terbanyak. Selain itu, Anda dapat pergi ke hasil turnamen individu "kelas melawan kelas" dan melihat bagaimana kelas menunjukkan diri mereka dalam pertempuran satu sama lain; seperti yang Anda lihat, kebanyakan dari mereka seimbang sangat merata - pada akhir pertempuran kedua kelas sedang sekarat, atau salah satu dari mereka nyaris tidak selamat. Selain itu, semua turnamen berlangsung cukup lama, tidak ada satu kelas pun yang dapat “mengalahkan” yang lain.

Tidak buruk untuk beberapa jam kerja, bukan?

Kesimpulan

Dalam contoh ini, kami membuat tugas penyeimbangan sederhana dan menunjukkan bahwa sebenarnya kami dapat menyelesaikannya dengan bantuan simulasi dan optimisasi. Meskipun jelas bahwa ini adalah contoh sederhana, ini menunjukkan kepada kita kekuatan teknik pemodelan dan optimisasi keputusan. Selain itu, ini dapat menjadi sumber inspirasi yang dapat digunakan dalam alat penyeimbang yang lebih kompleks, terintegrasi dengan kuat ke dalam simulasi permainan. Kami harap Anda dapat menggunakan contoh ini sebagai panduan untuk merumuskan tugas-tugas seperti itu dalam praktik.

Dalam dua bagian berikutnya dari seri, kita akan terjun ke bidang tugas penugasan, yang terkait dengan pemilihan penugasan optimal dari dua atau lebih set entitas. Kami akan menunjukkan cara mengatasi jenis masalah ini dan menunjukkan bagaimana kami menggunakan pendekatan ini untuk membuat desain menara dalam permainan strategi kami untuk iOS / Android City Conquest .