Saya membaca buku resmi tentang strategi perdagangan dan menulis robot perdagangan saya. Yang mengejutkan saya, robot itu tidak menghasilkan jutaan, bahkan berdagang secara virtual. Alasannya jelas: robot, seperti mobil balap, perlu "disetel", untuk memilih parameter yang disesuaikan dengan pasar tertentu, periode waktu tertentu.

Karena robot memiliki pengaturan yang cukup, iterasi semua kombinasi yang mungkin untuk mencari yang terbaik, juga tugas yang memakan waktu. Pada suatu waktu, menyelesaikan masalah optimasi, saya tidak menemukan pilihan yang masuk akal dari algoritma pencarian untuk vektor kuasi-optimal dari parameter robot perdagangan. Oleh karena itu, saya memutuskan untuk secara independen membandingkan beberapa algoritma ...

Pernyataan singkat tentang masalah optimasi

Kami memiliki algoritma perdagangan. Input data - riwayat harga interval per jam selama 1 tahun pengamatan. Data keluaran - P - untung atau rugi, nilai skalar.

Algoritma perdagangan memiliki 4 parameter yang dapat dikonfigurasi:

Mf adalah periode rata-rata bergerak "cepat",
Ms periode rata-rata bergerak "lambat"
T - TakeProfit, target level laba untuk setiap transaksi individu,
S - StopLoss, target level kerugian untuk setiap transaksi individu.

Kami menetapkan rentang dan langkah perubahan tetap untuk masing-masing parameter, total 20 nilai untuk masing-masing parameter.

Dengan demikian, kita dapat mencari keuntungan maksimum (P) untuk satu parameter pada satu array data input:

memvariasikan satu parameter, misalnya, P = f (Ms), menghasilkan hingga 20 uji ulang ,
memvariasikan dua parameter, misalnya, P = f (Ms, T), menghasilkan hingga 20 * 20 = 400 uji ulang,
memvariasikan tiga parameter, misalnya, P = f (Mf, Ms, T), menghasilkan hingga 20 * 20 * 20 = 8.000 backtests,
memvariasikan masing-masing parameter, P = f (Mf, Ms, T, S) dan menghasilkan hingga 20 ^ 4 = 160.000 uji ulang.

Namun, untuk sebagian besar algoritma perdagangan, dibutuhkan beberapa kali lipat lebih banyak waktu untuk melakukan pengujian tunggal. Yang mengarahkan kita pada tugas menemukan vektor parameter semu-optimal tanpa perlu mengulangi seluruh rangkaian kemungkinan kombinasi.

detail tentang robot perdagangan dan perdagangan

Berdagang di bursa saham, bertaruh di pusat transaksi Forex, bertaruh gila pada "opsi biner", spekulasi dengan cryptocurrency - semacam "diagnosis", dengan beberapa opsi yang memungkinkan untuk pengembangan "penyakit". Skenario yang sangat umum adalah ketika seorang pemain, setelah bermain "intuisi", datang ke perdagangan otomatis. Jangan salah paham, saya tidak ingin memberi penekanan sedemikian rupa sehingga robot-robot perdagangan yang ketat "secara teknologi dan matematis" menentang perdagangan "manual" yang naif dan tak berdaya. Sebagai contoh, saya sendiri yakin bahwa setiap upaya saya untuk mengambil keuntungan dari pasar yang efisien (baca dari pasar yang transparan dan likuid) melalui spekulasi, baik diskresioner atau sepenuhnya otomatis, adalah apriori yang ditakdirkan untuk gagal. Jika, mungkin, tidak memungkinkan faktor keberuntungan acak.

Namun, perdagangan, dan khususnya, perdagangan algo (ritmis), adalah hobi yang populer bagi banyak orang. Beberapa robot perdagangan program independen, yang lain melangkah lebih jauh dan membuat platform mereka sendiri untuk menulis, men-debug dan menguji strategi perdagangan, sementara yang lain mengunduh / membeli "pakar" elektronik yang sudah jadi. Tetapi bahkan mereka yang tidak menulis algoritma perdagangan sendiri, harus memiliki gagasan tentang bagaimana menangani "kotak hitam" ini untuk mendapat untung dari itu sesuai dengan ide penulis. Agar tidak berdasar, saya memberikan pengamatan lebih lanjut menggunakan contoh strategi perdagangan sederhana:

Robot perdagangan sederhana

Robot perdagangan menganalisis dinamika nilai emas, dalam dolar per troy ons, dan memutuskan untuk "membeli" atau "menjual" sejumlah emas. Untuk mempermudah, kami menganggap bahwa robot selalu berdagang dalam satu troy ons.

Misalnya, pada saat pembelian, biaya troy ounce emas adalah 1075,00 USD . Pada saat penjualan berikutnya (penutupan transaksi), harga naik menjadi 1079,00 USD. Keuntungan dari transaksi ini sebesar 4 USD.

Jika robot "menjual" emas pada 1075,00 USD, dan kemudian menyelesaikan (menutup) transaksi dengan "membeli" emas kembali pada harga 1079 USD, laba pada transaksi akan negatif - minus 4 USD. Sebenarnya, tidak masalah bagi kami bagaimana robot menjual emas, yang tidak dimilikinya, untuk kemudian “membelinya kembali”. Pialang / pusat transaksi memungkinkan pedagang untuk "membeli" dan "menjual" suatu aset dengan satu atau lain cara, menghasilkan (atau, lebih sering, kehilangan), pada selisih kurs.

Kami memutuskan data input untuk robot - ini, sebenarnya, rangkaian waktu harga (kutipan) emas. Jika Anda mengatakan bahwa contoh saya terlalu sederhana, tidak vital - saya dapat meyakinkan Anda: sebagian besar robot yang beredar di pasar (dan memang para pedagang juga) dalam perdagangan mereka hanya dipandu oleh statistik harga barang yang mereka perdagangkan. Bagaimanapun, dalam masalah optimasi parametrik dari strategi perdagangan, tidak ada perbedaan mendasar antara perdagangan robot berdasarkan vektor harga dan robot yang mengakses array terabyte dari analisis pasar multi-sortir. Hal utama adalah bahwa kedua robot ini dapat (harus dapat) diuji pada data historis. Algoritma harus ditentukan: yaitu, pada input data yang sama (waktu model, jika perlu, kita juga dapat menganggapnya sebagai parameter), robot perdagangan harus menunjukkan hasil yang sama.

Rincian lebih lanjut tentang robot perdagangan dapat ditemukan di spoiler berikut:

algoritma perdagangan robot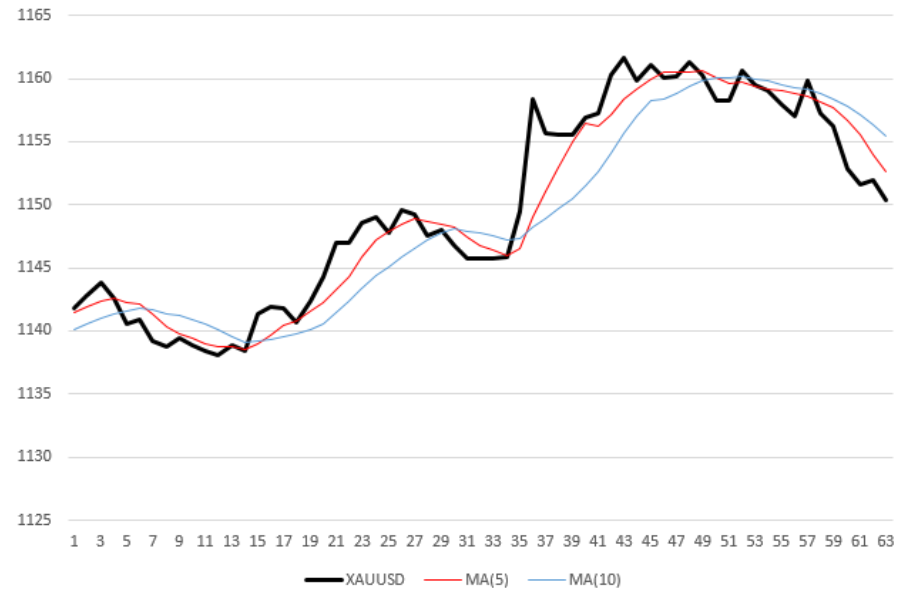

Kurva hitam (tebal) pada grafik adalah pengukuran harga XAUUSD per jam. Dua garis putus-putus tipis, nilai harga rata-rata merah dan biru dengan periode rata-rata masing-masing 5 dan 10. Dengan kata lain, Moving Average (MA) dengan periode 5, 10. Misalnya, untuk menghitung ordinasi titik (kanan) terakhir dari kurva merah, saya mengambil rata-rata dari 5 nilai harga terakhir. Dengan demikian, setiap moving average tidak hanya "dihaluskan" relatif terhadap kurva harga, tetapi juga tertinggal setengah dari periode relatif terhadap itu.

Aturan Pembukaan Transaksi

Robot memiliki aturan sederhana untuk membuat keputusan pembelian / penjualan:
- segera setelah rata-rata bergerak dengan periode pendek ("cepat" MA ) melintasi rata-rata bergerak dengan periode panjang ("lambat" MA) dari bawah ke atas, robot membeli aset (emas).

Segera setelah MA "cepat" melintasi MA "lambat" dari atas ke bawah, robot menjual aset. Pada gambar di atas, robot akan melakukan 5 transaksi: 3 penjualan pada waktu perangko 7, 31 dan 50 dan dua pembelian (nilai 16 dan 36).

Robot diperbolehkan untuk membuka jumlah transaksi yang tidak terbatas. Misalnya, pada titik tertentu, robot mungkin memiliki beberapa pembelian dan penjualan yang tertunda pada saat yang sama.

Aturan penutupan transaksi

Robot menutup kesepakatan segera setelah:

laba pada transaksi melebihi ambang yang ditentukan dalam persen - TakeProfit,
atau kerugian pada transaksi, dalam persen, melebihi nilai yang sesuai - StopLoss.

Misalkan StopLoss adalah 0,2%.
Kesepakatan itu adalah "penjualan" emas dengan harga 1061,50.
Segera setelah harga emas naik ke 1061.50 + 1061.50 * 0.2% / 100% = 1063.12%, kerugian pada kesepakatan jelas akan menjadi 0.2% dan robot akan menutup kesepakatan secara otomatis.

Robot membuat semua keputusan tentang membuka / menutup transaksi pada titik waktu yang berbeda - pada akhir setiap jam, setelah publikasi kutipan XAUUSD berikutnya.

Ya, robot ini sangat sederhana. Pada saat yang sama, 100% memenuhi persyaratan untuk itu:

Algoritma bersifat deterministik: setiap kali, mensimulasikan kerja robot pada data harga yang sama, kita akan mendapatkan hasil yang sama,
memiliki jumlah parameter penyesuaian yang cukup, yaitu: periode "cepat" dan periode "lambat" rata-rata bergerak (angka alami), TakeProfit dan StopLoss - angka real positif,
perubahan di masing-masing dari 4 parameter, dalam kasus umum, memiliki efek nonlinier pada karakteristik perdagangan robot, khususnya, pada profitabilitasnya,
profitabilitas robot pada sejarah harga dianggap sebagai kode program dasar, dan perhitungan itu sendiri membutuhkan sepersekian detik untuk vektor ribuan kutipan,
akhirnya, yang, bagaimanapun, tidak relevan, robot, dengan segala kesederhanaannya, pada kenyataannya akan terbukti tidak lebih buruk (walaupun mungkin tidak lebih baik) daripada Grail yang dijual oleh penulis di Internet dengan jumlah yang tidak sopan.

Pencarian cepat untuk set optimal parameter input semu

Dengan menggunakan contoh robot sederhana kami, dapat dilihat bahwa penghitungan lengkap semua kemungkinan vektor pengaturan robot terlalu mahal bahkan untuk 4 parameter variabel. Alternatif yang jelas untuk pencarian lengkap adalah pilihan vektor parameter untuk strategi tertentu. Kami menganggap hanya sebagian dari semua kombinasi yang mungkin untuk mencari yang terbaik, di mana CF mendekati tertinggi (atau terkecil, tergantung pada CF mana yang kami pilih dan hasil apa yang kami capai).

Kami akan mempertimbangkan tiga algoritma pencarian untuk nilai kuasi- optimal dari filter digital . Untuk setiap algoritma, kami menetapkan batas 40 tes (dari 400 kemungkinan kombinasi).

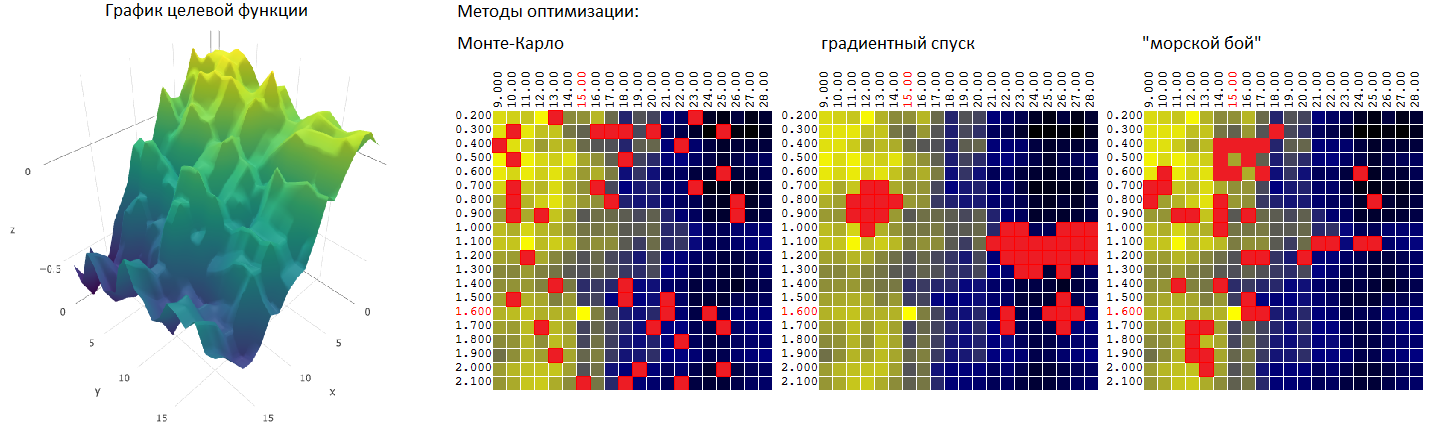
Metode Monte Carlo

atau pemilihan acak vektor tidak berkorelasi M dari antara jumlah set yang mungkin sama dengan N. Metode ini mungkin yang paling sederhana. Kami akan menggunakannya sebagai titik awal untuk perbandingan selanjutnya dengan metode optimasi lainnya.

Contoh 1

grafik menunjukkan ketergantungan pada laba (P) dari perdagangan robot kami, EURUSD , yang diperoleh pada segmen tahunan dari sejarah pengukuran harga per jam, pada nilai parameter - periode rata-rata bergerak lambat (M). Semua parameter lain sudah diperbaiki dan tidak dioptimalkan.

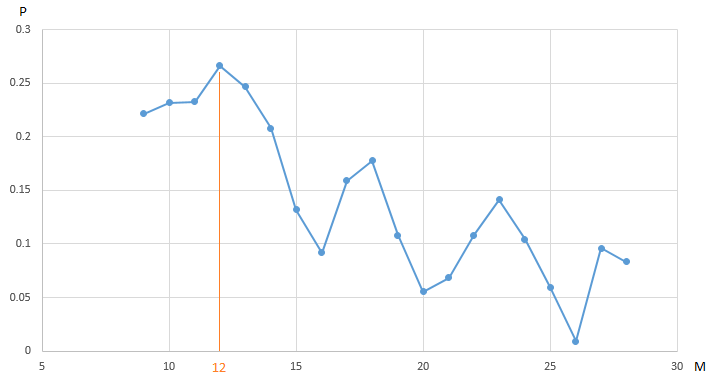
CF (laba) mencapai maksimum 0,27 pada titik M = 12. Untuk menjamin nilai maksimum laba, kita perlu melakukan 20 iterasi pengujian. Alternatifnya adalah dengan melakukan sejumlah kecil tes robot dagang dengan nilai parameter M yang dipilih secara acak pada interval [9, 20]. Misalnya, setelah 5 iterasi (20% dari total tes, kami menemukan vektor kuasi-optimal (vektor, jelas, satu dimensi) parameter: M = 18 dengan nilai CF (M) sama dengan 0,18:

Nilai yang tersisa pada grafik dari algoritme pengoptimalan kami disembunyikan oleh "kabut perang".

Optimalisasi salah satu dari empat parameter robot perdagangan kami, dengan nilai tetap dari parameter yang tersisa, tidak memungkinkan kami untuk melihat keseluruhan gambar. Mungkin maksimum 0,27 CF bukan nilai terbaik dari indikator, jika Anda memvariasikan nilai parameter lain?

Ini adalah bagaimana ketergantungan laba pada perubahan periode rata-rata bergerak untuk berbagai nilai parameter TakeProfit pada interval [0,2 ... 0,8].

Metode Monte Carlo: optimalisasi dua parameter

Ketergantungan keuntungan dari robot perdagangan pada dua parameter dapat digambarkan secara grafis sebagai permukaan:

Dua sumbu adalah nilai dari parameter T (TakeProfit) dan M (periode moving average), sumbu ketiga adalah nilai laba.

Untuk robot perdagangan kami, setelah melakukan 400 tes pada interval data satu tahun (~ 6000 kutipan per jam dari euro terhadap dolar AS), kami memperoleh permukaan formulir:

atau, pada bidang di mana nilai aset keuangan (laba, P) diwakili oleh warna:

Memilih titik sembarang di pesawat, dalam contoh ini, algoritme tidak menemukan nilai optimal, tetapi cukup dekat dengan itu:

Seberapa efektif metode Monte Carlo dalam menemukan CF maksimum? Setelah melakukan 1.000 iterasi mencari maksimum CF pada sumber data dari contoh di atas, saya mendapat statistik berikut:

nilai rata-rata maksimum DF yang ditemukan selama 1.000 iterasi optimasi (40 vektor acak parameter [M, T] dari 400 kemungkinan kombinasi) adalah 0,231 atau 95,7% dari maksimum global DF (0,279).

Jelas, dalam membandingkan metode optimasi parametrik robot perdagangan, satu sampel bukan merupakan indikator. Namun untuk saat ini, penilaian ini sudah cukup. Kita lanjutkan ke metode selanjutnya - metode gradient descent .

Metode keturunan gradien

Secara formal, seperti namanya, metode ini digunakan untuk mencari minimum DF.
Menurut metode, kami memilih titik awal dengan koordinat [x0, y0, z0, ...]. Pada contoh optimalisasi satu parameter, ini bisa menjadi titik yang dipilih secara acak:

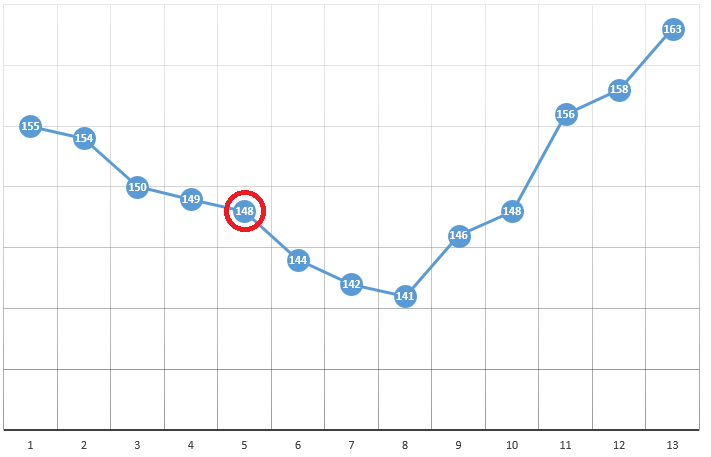
dengan koordinat [5] dan nilai DF 148. Berikut ini adalah tiga langkah sederhana:

periksa nilai CF di sekitar posisi saat ini (149 dan 144)
pindah ke titik dengan nilai CF terkecil
jika tidak ada, ekstrem lokal ditemukan, algoritme selesai

Untuk mengoptimalkan DF sebagai fungsi dari dua parameter, kami menggunakan algoritma yang sama. Jika sebelumnya kita menghitung CF di dua titik tetangga

[x_{i - 1}], [x_{i + 1}]

$[x_ {i-1}], [x_ {i + 1}]$ , sekarang kita periksa 4 poin:

[x_{i - 1}, y_{i}], [x_{i + 1}, y_{i}], [x_{i}, y_{i - 1}], [x_{i}, y_{i + 1}] .

$[x_ {i-1}, y_i], [x_ {i + 1}, y_i], [x_i, y_ {i-1}], [x_i, y_ {i + 1}].$

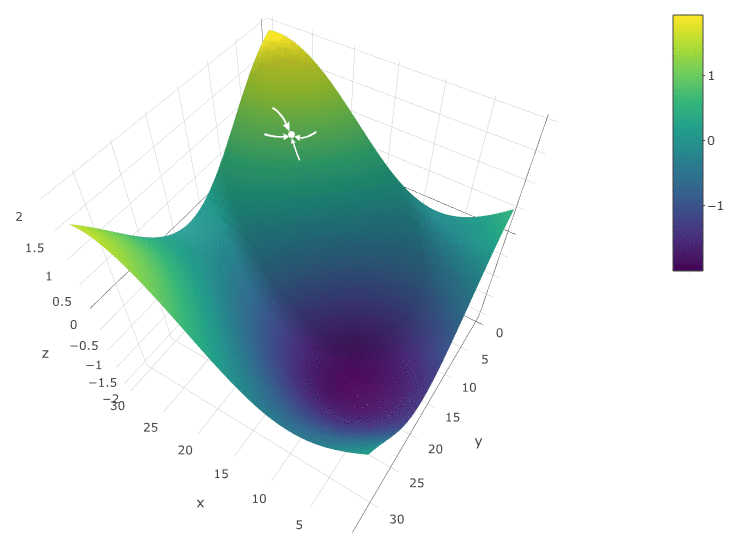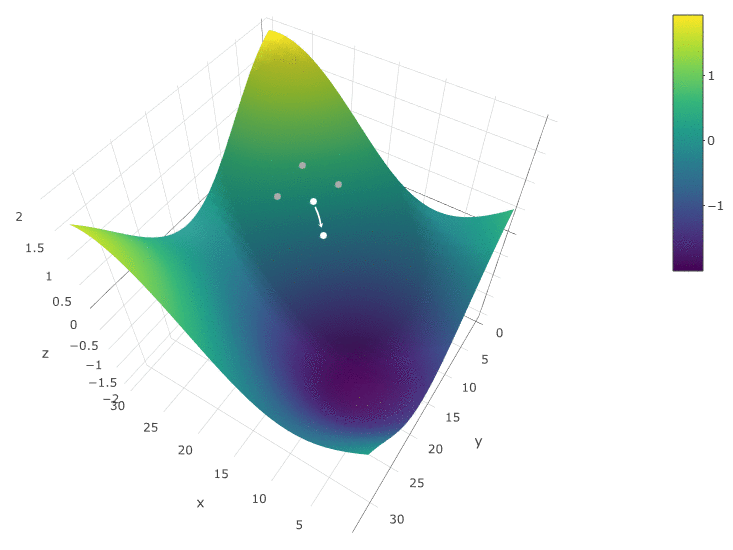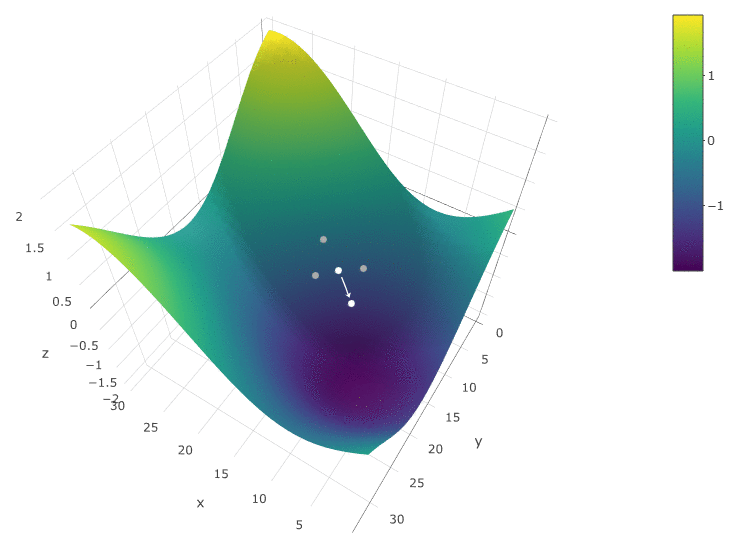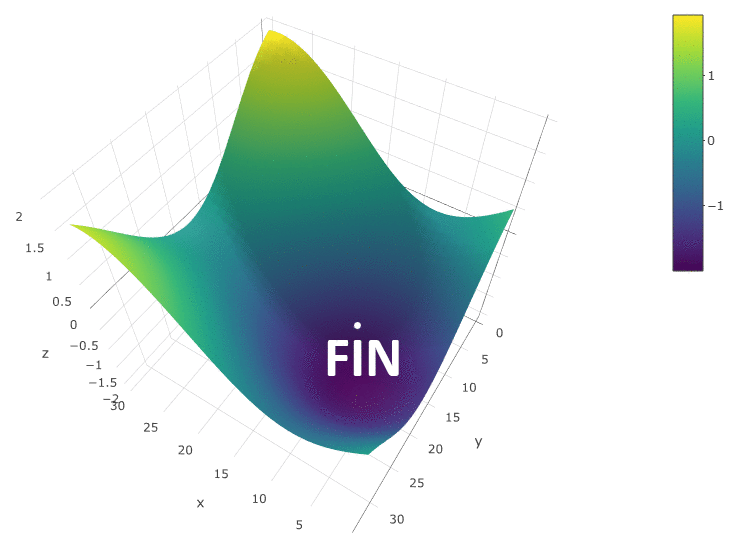
Metode ini pasti baik ketika hanya ada satu ekstrem di DF dalam ruang uji. Jika ada beberapa ekstrem, pencarian harus diulang beberapa kali untuk meningkatkan kemungkinan menemukan ekstrem global:

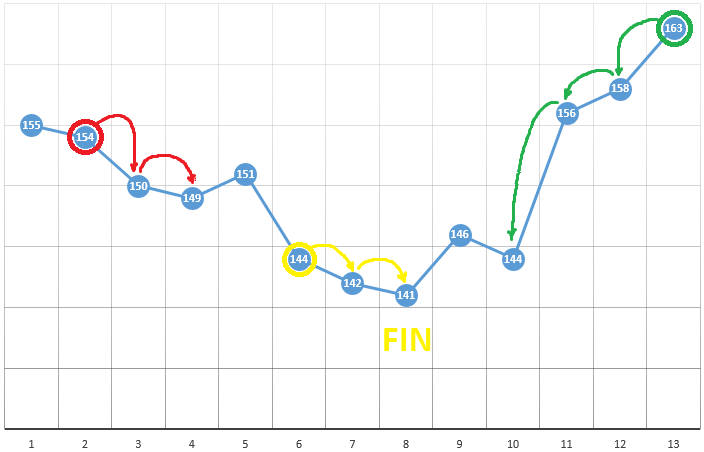
Dalam contoh kami, kami sedang mencari DF maksimum . Untuk tetap dalam definisi algoritma, kita dapat mengasumsikan bahwa kami sedang mencari minimum "minus DF". Semua contoh yang sama, keuntungan dari robot perdagangan sebagai fungsi periode moving average dan nilai TakeProfit, satu iterasi:

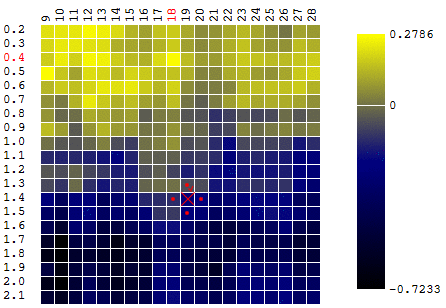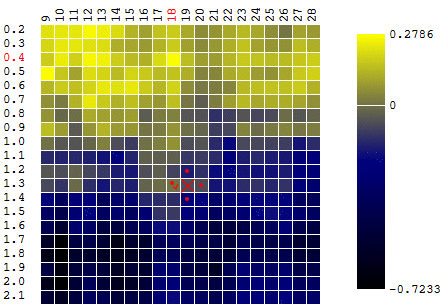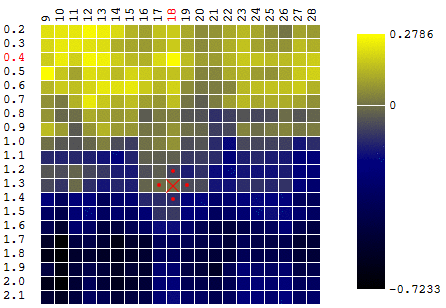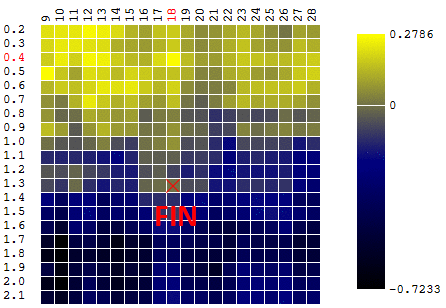
Dalam kasus ini, ditemukan suatu ekstrem lokal yang jauh dari maksimum global CF. Contoh dari beberapa iterasi pencarian untuk ekstrem FS dengan metode gradient descent, nilai FS dihitung 40 kali (40 poin dari 400 kemungkinan):

Sekarang, kami membandingkan efisiensi pencarian maksimum global CF (laba) pada data awal kami menggunakan Monte Carlo dan algoritma gradient descent. Dalam setiap kasus, 40 tes dilakukan (perhitungan CF). 1.000 iterasi optimasi dilakukan oleh masing-masing metode:

	Monte Carlo	keturunan gradien
rata-rata nilai kuasi-optimal yang diperoleh CF	0,231	0,200
nilai yang diperoleh dari maksimum CF	95,7%	92,1%

Seperti yang dapat Anda lihat dari tabel, dalam contoh ini, metode gradient descent lebih buruk dalam tugasnya - untuk mencari ekstrem global dari aset digital - keuntungan maksimum. Tapi kita tidak terburu-buru membuangnya.

Stabilitas parametrik dari algoritma perdagangan

Menemukan koordinat maksimum / minimum global dari filter digital sering kali bukan tujuan pengoptimalan. Misalkan, pada grafik, ada puncak "tajam" - maksimum global, nilai CF di sekitarnya yang jauh lebih rendah daripada nilai puncak:

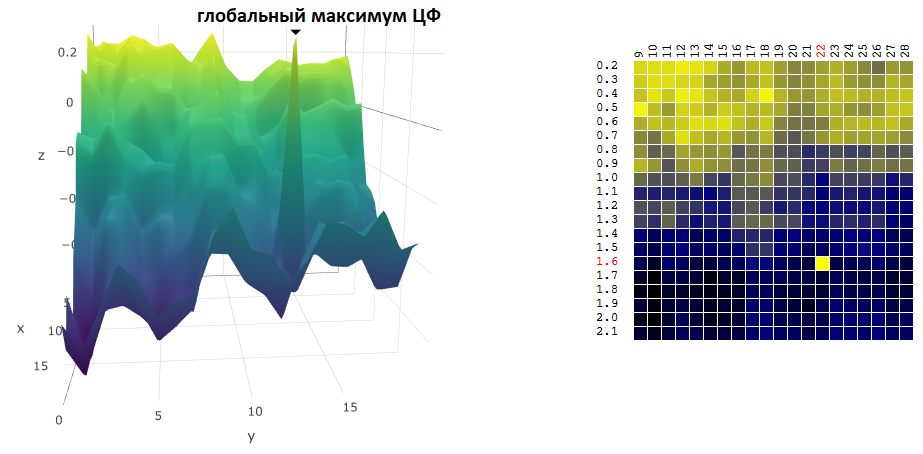
Misalkan kita telah memilih pengaturan robot perdagangan yang sesuai dengan maksimum yang ditemukan dari aset digital. Jika kita sedikit mengubah nilai setidaknya satu dari parameter - periode moving average dan / atau TakeProfit - profitabilitas robot akan turun tajam (menjadi negatif). Berkenaan dengan perdagangan nyata, setidaknya kita bisa berharap bahwa pasar di mana robot kita untuk melakukan perdagangan akan sangat berbeda dari periode sejarah di mana kita mengoptimalkan algoritma perdagangan.

Oleh karena itu, ketika memilih pengaturan "optimal" dari robot perdagangan, ada baiknya untuk mengetahui seberapa sensitif robot terhadap perubahan dalam pengaturan di sekitar titik ekstrem yang ditemukan dari DF.

Jelas, metode gradient descent, sebagai aturan, memberi kita nilai-nilai TF di sekitar ekstrem. Metode Monte Carlo lebih cenderung mengenai kuadrat.

Dalam beberapa instruksi untuk menguji strategi perdagangan otomatis, setelah optimasi selesai, disarankan untuk memeriksa indikator target robot di sekitar vektor parameter yang ditemukan. Tapi ini adalah tes tambahan. Selain itu, bagaimana jika profitabilitas strategi turun dengan sedikit perubahan dalam pengaturan? Jelas, Anda harus mengulangi proses pengujian.

Algoritma akan berguna bagi kami, yang, pada saat yang sama dengan mencari ekstrem CF, akan memungkinkan kami untuk mengevaluasi stabilitas strategi perdagangan untuk mengubah pengaturan dalam kisaran sempit sehubungan dengan puncak yang ditemukan. Misalnya, jangan langsung mencari CF maksimum

P = f (m_{i}, t_{i}),

$P = f (m_i, t_i),$

dan nilai rata-rata tertimbang yang memperhitungkan nilai tetangga dari fungsi objektif, di mana bobot berbanding terbalik dengan jarak ke nilai tetangga (untuk mengoptimalkan dua parameter x, y dan fungsi objektif P):

P^{'} (x_{i}, y_{i}) = f r a c w_{i} k a l i P (x_{i}, y_{i}) + w_{j} k a l i P (x_{j}, y_{j}) + w_{k} k a l i P (x_{k}, y_{k}) + . . . w_{i} + w_{j} + w_{k} + . . .

$P '(x_i, y_i) = \ frac {w_i \ kali P (x_i, y_i) + w_j \ kali P (x_j, y_j) + w_k \ kali P (x_k, y_k) + ...} {w_i + w_j + w_k + ...}$

w_{j} = s q r t (x_{j} - x_{i})^{2} + (y_{j} - y_{i})^{2}

$w_j = \ sqrt {(x_j-x_i) ^ 2 + (y_j-y_i) ^ 2}$

w_{i} + w_{j} + w_{k} + . . . = 1

$w_i + w_j + w_k + ... = 1$

Dengan kata lain, ketika memilih vektor kuasi-optimal parameter, algoritma akan mengevaluasi fungsi tujuan "dihaluskan":

adalah

telah menjadi

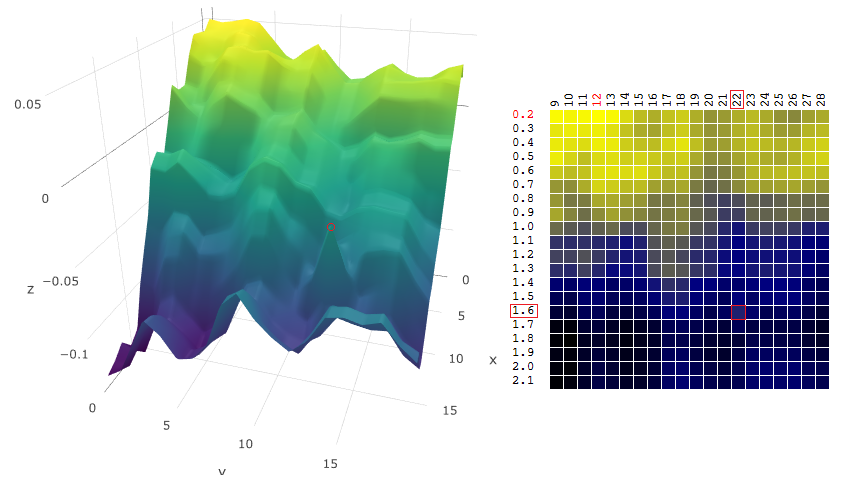
Metode "pertempuran laut"

Mencoba untuk menggabungkan keuntungan dari kedua metode (Monte Carlo dan metode gradient descent), saya mencoba algoritma yang mirip dengan algoritma permainan di "pertempuran laut":

pertama, saya melakukan beberapa "pukulan" di seluruh area
kemudian, di tempat-tempat "hit" saya melepaskan tembakan besar-besaran.

Dengan kata lain, tes N pertama dilakukan pada vektor parameter input yang tidak berkorelasi acak. Dari jumlah tersebut, hasil M terbaik dipilih. Di sekitar tes ini (ditambah - menit 0..L untuk masing-masing koordinat) tes K lainnya dilakukan.

Sebagai contoh kami (total 400 poin, 40 percobaan) kami memiliki:

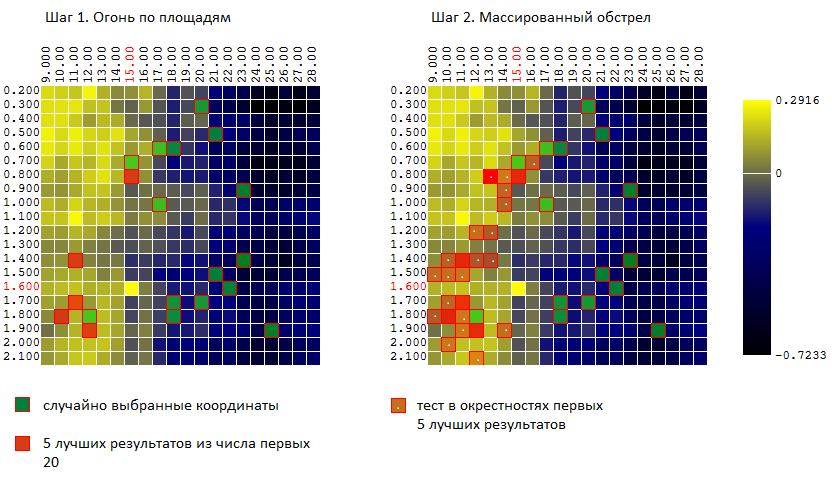
Dan lagi, kami membandingkan efektivitas sekarang 3 algoritma optimasi:

	Monte Carlo	keturunan gradien	"Pertempuran laut"
Nilai rata-rata dari ekstrum CF yang ditemukan sebagai persentase dari nilai global. 40 tes, 1.000 iterasi optimasi	95,7%	92,1%	97,0%

Hasilnya menggembirakan. Tentu saja, perbandingan dilakukan pada satu sampel data spesifik: satu algoritma perdagangan pada satu seri waktu dari nilai euro terhadap dolar AS.Tetapi, sebelum membandingkan algoritme dengan sampel sampel sumber yang lebih banyak, saya akan membahas tentang algoritma lain yang tidak terduga (tidak dapat dibenarkan?) Populer untuk mengoptimalkan strategi perdagangan - optimasi algoritma genetika (GA). Namun, artikel itu keluar terlalu banyak, dan GA harus ditunda untuk publikasi berikutnya .

Algoritma untuk mengoptimalkan robot perdagangan: cara efektif untuk berdagang sejuta secara retroaktif