Ada beberapa tugas di mana sinyal lama dibagi menjadi beberapa segmen, yang masing-masing diproses secara terpisah. Secara khusus, pendekatan ini digunakan untuk menganalisis sinyal menggunakan transformasi Fourier, atau sebaliknya, dalam sintesis; serta dalam pemrosesan spektral seperti penghapusan noise, perubahan tempo, pemfilteran non-linear, kompresi data audio dan lainnya.

Proses partisi itu sendiri secara matematis diwakili oleh perkalian dengan beberapa fungsi berat ( jendela ) dengan offset. Untuk jendela paling sederhana - persegi panjang - mungkin terlihat seperti ini:

Sinyal sumber:



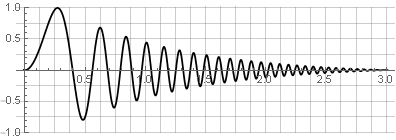
Partisi:







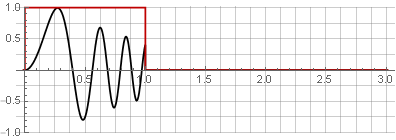
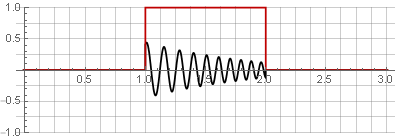
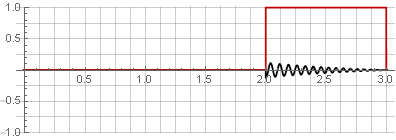
Anda dapat mengembalikan sinyal asli hanya dengan menambahkannya.

Lebih detail

Namun oleh Untuk sejumlah alasan, fungsi persegi panjang bukan fungsi jendela terbaik. Dalam analisis spektral, melalui transformasi Fourier diskrit (biasanya cepat), blok data yang dianalisis tampaknya "loop", yang mengarah ke celah di tepi dan distorsi spektrum:



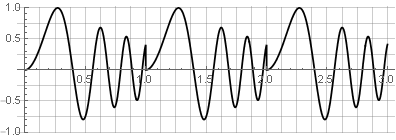
Ini juga tidak cocok untuk sintesis terbalik - karena perubahan apa pun juga akan menyebabkan jeda - misalnya, jika kita mencoba membalik salah satu bagian:



Untuk menghilangkan kelemahan ini, tumpang tindih digunakan - ketika setiap jendela berikutnya menangkap bagian dari data dari yang sebelumnya; dan jendela berat, masing-masing, secara bertahap jatuh ke tepi.

Tumpang tindih di 50%

Paling sering mereka menggunakan jendela Hannah (juga dikenal sebagai "cosinus terangkat") dengan tumpang tindih 50%:








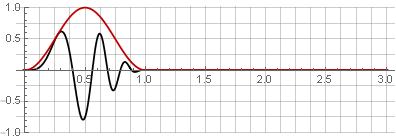
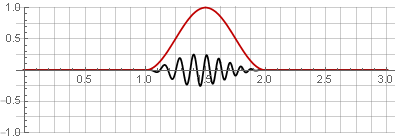
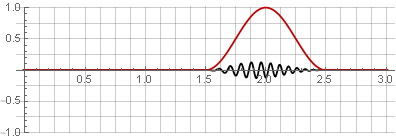
Karena simetri fungsi cosinus selama penambahan, mereka dijumlahkan menjadi satu:



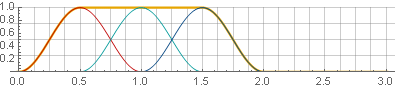
Sekarang, dengan sintesis terbalik, kita tidak akan mendapatkan celah - tetapi hanya dengan syarat bahwa pada batas-batas jendela nilai-nilai masih akan pergi ke nol. Misalnya, saat membalikkan salah satu bagian, kehalusan tidak akan dilanggar:

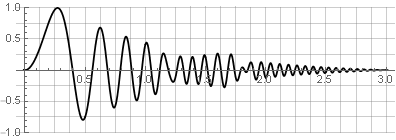
Pemrosesan Hamparan Ganda

Pertimbangkan lebih detail algoritme untuk memproses sinyal menggunakan fast Fourier transform (FFT):

1. memisahkan sinyal menjadi segmen-segmen dengan overlay jendela;
2. FFT langsung;
3. pemrosesan spektrum;
4. FFT terbalik;
5. overlay jendela berulang (karena setelah FFT terbalik, batas tidak harus merapat ke nol tanpa merusak);
6. penjumlahan dari segmen yang dihasilkan.

Selain itu, jika pemrosesan spektrum tidak dilakukan, sinyal output harus identik dengan sinyal input (hanya dengan penundaan waktu yang tak terelakkan).

Saat menggunakan jendela Hann, tumpang tindih 50% tidak lagi cukup, karena akan terjadi penurunan:



Karena tumpang tindih ganda sama dengan mengkuadratkan, solusi yang jelas adalah dengan menggunakan root dari jendela Hann untuk mengimbangi mengkuadratkan:



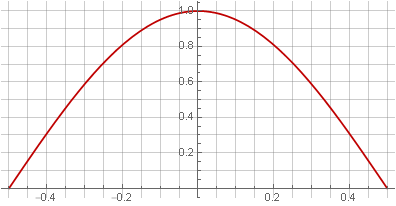
Namun, dalam kasus ini, jendela tidak lagi mulus di tepinya - celah muncul pada turunan pertama.


Anda dapat pergi ke arah lain - gunakan tumpang tindih 75%, dan kemudian jendela juga akan dijumlahkan menjadi konstan - hanya saja tidak di $$$1$ , dan dalam $$$\ frac {3} {2}$ :



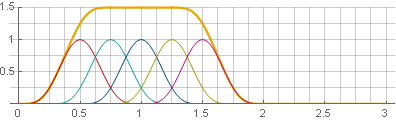
Dalam hal ini, kami beruntung. Jika kita memperluas kuadrat menjadi jumlah, maka kita dapat melihat bahwa itu adalah komposisi dari dua jendela Hannah, tetapi pada skala yang berbeda, yang memungkinkan kita untuk memenuhi persyaratan yang kita butuhkan:

$$

$$\ kiri (\ frac {\ cos (2 \ pi x) +1} {2} \ kanan) ^ 2 = \ frac {\ cos (2 \ pi x) +1} {2} + \ frac {\ cos (4 \ pi x) -1} {8}$$

Dengan fungsi jendela lainnya, trik semacam itu tidak akan berfungsi; Juga, tidak semua fungsi jendela standar dapat memberikan penjumlahan dalam konstanta bahkan pada 50% tumpang tindih.

Ide

Kita dapat menganggap jendela Hann bukan sebagai fungsi independen, tetapi sebagai perbedaan antara dua fungsi kontinu yang terpisah (artikel terpisah dikhususkan untuk diskusi terperinci tentang mereka) dengan offset. Misalnya, menggunakan fungsi berikut

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ \ sin \ kiri (\ frac {\ pi x} {2} \ kanan) & -1 <x <1 \\ \ end {array} \ benar.$$

bisa menulis

$$

$$f (x + 1) -f (x-1)$$

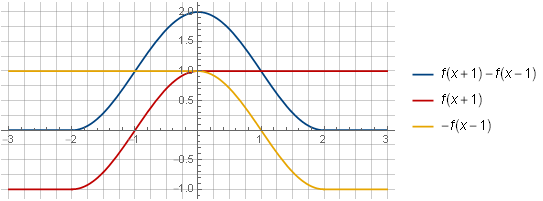
Setelah mempertimbangkan komponen-komponen dari penjumlahan dua jendela tersebut, kemampuan mereka untuk meringkas menjadi sebuah konstanta akan menjadi lebih visual:



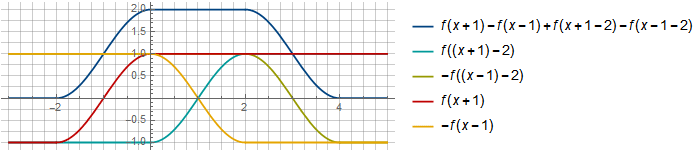
Di segmen tersebut $$$[0,2]$ kami menerima kompensasi timbal balik sebagai tambahan fungsi $$$-f (x-1)$ dan $$$f ((x + 1) -2)$ sejak itu $$$f ((x + 1) -2) = f (x-1)$

Anda dapat memilih offset lain, dengan lebih banyak tumpang tindih, misalnya:

$$

$$f \ kiri (x + \ frac {1} {2} \ kanan) -f \ kiri (x- \ frac {1} {2} \ kanan)$$

Dan kemudian, saat bergeser dalam langkah-langkah $$$\ frac {1} {2}$ , mereka juga akan dijumlahkan menjadi sebuah konstanta:



Dapat dilihat bahwa jika Anda mengatur ulang komponen fungsi jendela, Anda mendapatkan jendela Hann yang sama.

Dengan demikian, menggunakan fungsi pembatasan yang berbeda, dimungkinkan untuk membentuk jendela dari bentuk yang diperlukan.

Formula akhir

Sekarang tinggal mengatur skala agar area dan nilai definisi tidak bergantung pada jumlah tumpang tindih. Mendefinisikan jendela pada suatu interval $$$[0,1]$ kita dapatkan

$$

$$\ frac {f \ kiri (\ frac {2 tx} {t-1} -1 \ kanan) -f \ kiri (\ frac {2 t (x-1)} {t-1} +1 \ kanan) } {2}$$

dimana $$$f$ - fungsi bentuk kontinu piecewise

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ g (x) & -1 <x <1 \\ \ end {array} \ benar$$

tapi $$$g$ - beberapa fungsi interpolasi antar titik $$$(- 1, -1)$ dan $$$(1,1)$ .

Parameter $$$t$ menentukan tingkat tumpang tindih - pembagi yang menentukan langkah di mana setiap jendela berikutnya harus digeser, $$$x_ {n + 1} = x_n + \ frac {1} {t}$ , dan harus lebih besar dari satu, $$$t> 1$ .

Persentase yang tumpang tindih $$$p$ dapat dihitung dengan rumus

$$

$$p = \ frac {100 (t-1)} {t}$$

dan sebaliknya

$$

$$t = \ frac {100} {100-p}$$

Tampilan akhir jendela akan tergantung pada pilihan tingkat tumpang tindih dan pilihan fungsi pembatas.

Beberapa contoh menarik

Di sini kita akan melihat beberapa solusi siap pakai, yang semuanya dimulai. Untuk kesederhanaan, kami mempertimbangkan fungsi interpolasi sederhana $$$g (x)$ , tanpa tali pengikat lainnya.

Jendela polinomial

Mereka adalah yang paling tidak mahal secara komputasi. Menggunakan rumus yang diturunkan sebelumnya

$$

$$\ frac {2 x \ Gamma \ kiri (n + \ frac {1} {2} \ kanan) \, _2F_1 \ kiri (\ frac {1} {2}, 1-n; \ frac {3} {2} ; x ^ 2 \ kanan)} {\ sqrt {\ pi} \ Gamma (n)}$$

kami memperoleh polinomial dengan jumlah nol tertentu pada turunan yang lebih tinggi yang memberikan kelancaran yang diperlukan dari jendela di tepinya.


Dengan 75% tumpang tindih jendela dengan nilai n yang berbeda, jendela akan terlihat seperti ini:



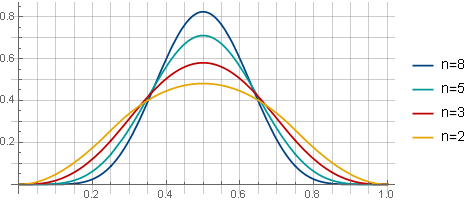
Dan dalam kasus ekstraksi root - seperti ini (saat menggunakan 75% tumpang tindih):



atau lebih (saat menggunakan 50% tumpang tindih):

Jendela paling halus

Fungsi

$$

$$\ tanh \ kiri (\ frac {k x} {\ sqrt {1-x ^ 2}} \ kanan)$$

Sangat menarik karena dapat terdiferensiasi tanpa batas dan semua turunannya di tepinya adalah 0 (yang dapat dibuktikan dengan mempertimbangkan turunannya berdasarkan aturan diferensiasi - dalam setiap istilah akan ada faktor nol). Ini memungkinkan kami untuk membangun windows berdasarkan basisnya, semua turunannya tidak memiliki celah:

"Rok" tampilan jendela

Kebutuhan untuk jenis jendela ini disebabkan oleh peningkatan resolusi FFT, tetapi mengurangi efek "ketidakpastian frekuensi waktu" pada frekuensi tinggi dengan meningkatkan konsentrasi mereka di tengah.

Pertama, kami menentukan jenis fungsi jendela yang diinginkan - misalnya, sebagai berikut:

$$

$$- \ log \ kiri (k ^ 2 x ^ 2 + 1 \ kanan) + \ log \ kiri (k ^ 2 + 1 \ kanan) - \ frac {k ^ 2 \ kiri (1-x ^ 2 \ kanan) } {k ^ 2 + 1}$$

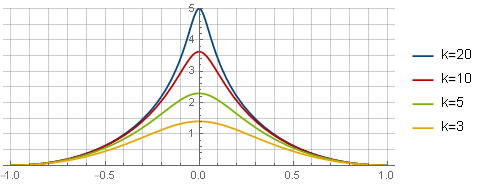
Di sini, istilah pertama menentukan bentuk fungsi itu sendiri, yang kedua - menyediakan persimpangan dengan sumbu absis, yang ketiga (parabola) mengatur ulang turunan di tepi untuk docking yang halus; dan parameternya $$$k$ mendefinisikan "ketajaman" puncak. Dalam formulir ini, itu belum cocok untuk digunakan - pertama Anda perlu mendapatkan fungsi pembatasan dari itu melalui integrasi dan penskalaan:

$$

$$\ frac {kx \ kiri (k ^ 2 \ kiri (x ^ 2 + 3 \ kanan) +6 \ kanan) +3 \ kiri (k ^ 2 + 1 \ kanan) \ kiri (kx \ kiri (\ log \ kiri (k ^ 2 + 1 \ kanan) - \ log \ kiri (k ^ 2 x ^ 2 + 1 \ kanan) \ kanan) -2 \ tan ^ {- 1} (kx) \ kanan)} {4 k ^ 3-6 \ kiri (k ^ 2 + 1 \ kanan) \ tan ^ {- 1} (k) +6 k}$$

Untuk kenyamanan, Anda dapat mengikat parameter $$$k$ ke tingkat tumpang tindih $$$t$ - misalnya, sehingga turunan ke-4 di tengah jendela adalah 0 - dan kemudian $$$k$ akan dianggap sebagai $$$\ sqrt {3} (t-1)$ :



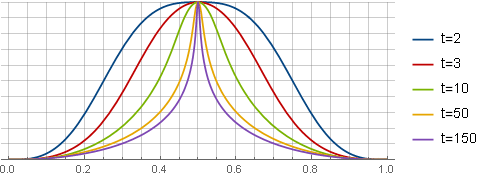
Di sini, untuk kejelasan, semua jendela dikurangi ke skala yang sama.

Jendela Tampilan Jarum

Ini adalah versi yang lebih "agresif" dari jendela sebelumnya. Hiperbola dipilih sebagai dasar, yang darinya, melalui transformasi yang berurutan

$$

$$\ frac {1} {x} \ to \ frac {1} {\ sqrt {x ^ 2}} \ to \ frac {1} {\ sqrt {x ^ 2 + 1}} \ to \ frac {1} {\ sqrt {k ^ 2 x ^ 2 + 1}} \ to \ frac {\ left (1-x ^ 2 \ right) ^ 2} {\ sqrt {k ^ 2 x ^ 2 + 1}}$$

dan menggunakan langkah yang sama dalam bentuk integrasi dan penskalaan mendapatkan formula

$$

$$\ frac {kx \ kiri (2 k ^ 2 \ kiri (x ^ 2-4 \ kanan) -3 \ kanan) \ sqrt {k ^ 2 x ^ 2 + 1} + \ kiri (8 \ kiri (k ^ 4 + k ^ 2 \ kanan) +3 \ kanan) \ sinh ^ {- 1} (kx)} {\ kiri (8 \ kiri (k ^ 4 + k ^ 2 \ kanan) +3 \ kanan) \ sinh ^ {-1} (k) -3 k \ sqrt {k ^ 2 + 1} \ kiri (2 k ^ 2 + 1 \ kanan)}$$

Di sini Anda juga dapat mengikat parameter $$$k$ ke tingkat tumpang tindih. Solusi langsung dari persamaan derivatif ke-4 memberikan hasil yang rumit, jadi buat saja gambar untuk jendela sebelumnya pada gambar dan rupa dengan mendefinisikan $$$k$ bagaimana $$$k (t-1)$ dengan demikian memastikan peran parameter $$$k$ sebagai "fine tuning". Di $$$k = 2.22$ jendela akan terlihat seperti ini:

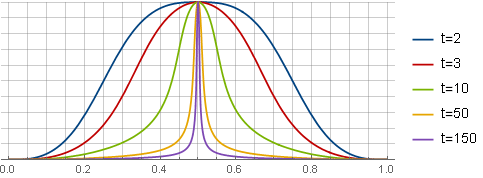
Jendela asimetris

Fungsi jendela tidak harus simetris sama sekali. Katakanlah kita membutuhkan jendela dengan serangan tajam dan atenuasi yang halus. Kita bisa mendapatkannya sesuai dengan skema yang sudah akrab - pertama menentukan bentuk fungsi yang diinginkan, dan kemudian dengan integrasi kita memperoleh fungsi pembatasan. Di sini tugasnya sedikit lebih rumit karena fakta bahwa, karena asimetri, pusat tidak akan lagi melewati titik asal, sehingga langkah perhitungan tambahan ditambahkan. Ini juga mengarah pada fakta bahwa formula sebagai hasilnya agak rumit. Misalnya, pertimbangkan opsi paling sederhana - parabola dikalikan dengan jendela bobot polinomial:

$$

$$(1-x) ^ 2 \ kiri (1-x ^ {10} \ kanan) ^ 2$$

Di sini, derajat x di jendela tertimbang (yaitu 10) menentukan "ketajaman" serangan. Kami menggunakan nilai tertentu, bukan parameter simbolis, untuk menyederhanakan rumus untuk kejelasan - jika Anda mau, Anda bisa menghitung ulang nanti.

Setelah integrasi, penskalaan tidak lagi cukup - Anda masih perlu menyelaraskan tepi:



Untuk melakukan ini, pertama-tama kita menggeser fungsi ke atas untuk menyelaraskan tepi kiri, dan kemudian skala ke dua di tepi kanan dan kurangi satu. Lalu kita mendapatkan formula berikut:

$$

$$\ frac {8775 \ kiri (\ frac {x ^ {27}} {27} - \ frac {2 x ^ {26}} {26} + \ frac {x ^ {25}} {25} - \ frac {2 x ^ {15}} {15} + \ frac {4 x ^ {14}} {14} - \ frac {2 x ^ {13}} {13} + \ frac {x ^ 3} {3} -x ^ 2 + x + \ frac {117592} {61425} \ kanan)} {9856} -1$$

Agar jendela akhir memiliki tampilan yang diinginkan, Anda juga perlu memberikan tingkat tumpang tindih yang cukup besar:

Kesimpulan

Demikian pula, Anda dapat membangun jendela dari fungsi berbentuk lonceng lainnya - misalnya, Gaussians; dan Anda juga dapat memodifikasi yang sudah dianggap memberikan kehalusan yang lebih besar atau mengubah bentuk kurva.

Karena pertimbangan, komposisi spektral fungsi jendela seperti itu tetap ada - studi terpisah harus dikhususkan untuk ini.

Versi artikel yang sedikit lebih maju (dengan kemampuan mengubah parameter di jendela secara dinamis dengan pertimbangan dan formula tersembunyi) dalam bentuk dokumen Wolfram Mathematica dapat diunduh di sini .