🛕 🙍🏼 🍠 Berapa banyak programmer yang Anda butuhkan untuk mendukung kode yang ditulis sebelumnya? 🤾🏿 👼🏿 💲

Beberapa waktu yang lalu, terjadi percakapan antara saya dan teman baik saya, di mana frasa berikut berbunyi:

- Jumlah programmer akan terus bertambah - karena jumlah kode bertambah, dan semakin banyak pengembang yang terus-menerus diperlukan untuk mendukungnya.
- Tapi kodenya sudah menua, bagian dari itu meninggalkan dukungan. Kehadiran semacam keseimbangan tidak dikesampingkan.

Mengingat mereka beberapa hari kemudian, saya bertanya-tanya apakah dukungan kode, yang membutuhkan lebih banyak dan lebih banyak sumber daya dari waktu ke waktu, pada akhirnya dapat melumpuhkan pengembangan fungsionalitas baru, atau akan membutuhkan peningkatan yang tidak terbatas dalam jumlah programmer? Analisis matematis dan persamaan diferensial membantu menilai secara kualitatif ketergantungan volume dukungan pada pengembangan dan menemukan jawaban atas pertanyaan.

Pertanyaan pertama. Bisakah mendukung "memakan" semua sumber daya pengembangan?

Pertimbangkan tim pemrogram yang jumlah pesertanya konstan. Bagikan waktu kerja mereka

m u (t)

$\ mu (t)$ (

0 < m u (t) < 1

$0 <\ mu (t) <1$ ) dicatat oleh pengembangan kode baru, dan sebagian kecil dari waktu

1 - m u (t)

$1- \ mu (t)$ pergi untuk mendukung. Di bawah asumsi model, anggap bahwa jenis kegiatan pertama ditujukan untuk meningkatkan jumlah kode, dan yang kedua - mengubahnya (mengoreksi kesalahan) dan tidak secara signifikan mempengaruhi jumlah kode.

Kami menunjukkan

y (t)

$y (t)$ semua kode ditulis oleh waktu

t

$t$ . Mengingat kecepatan penulisan kode adalah proporsional

m u (t)

$\ mu (t)$ kami mendapatkan:

f r a c d y (t) d t = a_{0} m u (t); a_{0} i n m a t h b b R, a_{0} > 0.

$\ frac {dy (t)} {dt} = a_0 \ mu (t); a_0 \ in \ mathbb {R}, a_0> 0.$

Adalah wajar untuk berasumsi bahwa tenaga kerja yang terlibat dalam mempertahankan kode sebanding dengan volumenya:

1 - m u (t) = a_{1} y (t); a_{1} i n m a t h b b R, a_{1} > 0

$1- \ mu (t) = a_1 y (t); a_1 \ in \ mathbb {R}, a_1> 0$

atau

m u (t) = 1 - a_{1} y (t)

$\ mu (t) = 1-a_1y (t)$

Dari mana

f r a c d y (t) d t = a_{0} (1 - a_{1} y (t))) .

$\ frac {dy (t)} {dt} = a_0 (1-a_1y (t))).$

Kami mendapatkan persamaan diferensial yang terintegrasi dengan mudah. Jika pada saat awal jumlah kode adalah nol, maka

y (t) = f r a c 1 a_{1} (1 - e^{- a_{0} a_{1} t}) .

$y (t) = \ frac {1} {a_1} (1-e ^ {- a_0a_1t}).$

t h i n g g a + i n f t y

$t \ hingga + \ infty$ fungsi

y (t) t o 1 / a_{1}

$y (t) \ to1 / a_1$ , dan

m u (t) h i n g g a 0

$\ mu (t) \ hingga 0$ . Dan ini berarti pengurangan bertahap seiring waktu pengembangan fungsionalitas baru menjadi nol dan transisi semua sumber daya untuk mendukung.

Namun, jika tepat waktu

h > 0

$h> 0$ Karena kode menjadi usang dan tidak lagi didukung, jumlah kode yang membutuhkan dukungan pada suatu waktu

t

$t$ sama dengan

y (t) - y (t - h) .

$y (t) - y (t-h).$ Lalu

1 - m u (t) = a_{1} (y (t) - y (t - h)),

$1- \ mu (t) = a_1 (y (t) - y (t-h)),$

m u (t) = 1 - a_{1} (y (t) - y (t - h)),

$\ mu (t) = 1-a_1 (y (t) - y (t-h)),$

tapi

y (t)

$y (t)$ adalah solusi persamaan diferensial dengan argumen tertunda [1]:

f r a c d y (t) d t = a_{0} (1 - a_{1} (y (t) - y (t - h))) .

$\ frac {dy (t)} {dt} = a_0 (1-a_1 (y (t) - y (t-h))).$

Solusi untuk persamaan ini ditentukan secara unik dengan menetapkan nilai-nilai

y (t)

$y (t)$ "Sebelum awal waktu", dengan

t i n [- h, 0]

$t \ in [-h, 0]$ . Karena tidak ada kode yang ditulis sebelum waktu awal, dalam kasus kami

y (t) = 0

$y (t) = 0$ di

t i n [- h, 0]

$t \ in [-h, 0]$ .

Mari kita lihat beberapa contoh. Kami akan mengukur waktu dalam tahun, dan jumlah kode dalam ribuan baris. Lalu untuk

a_{0}

$a_0$ Nilai urutan puluhan dapat diterima, kita ambil 50 dan 100. Artinya, dalam setahun tim pengembang akan menulis masing-masing lima puluh dan seratus ribu baris kode. Untuk

a_{1}

$a_1$ nilai yang dapat diterima mungkin:

0, 25 / a_{0}

$0,25 / a_0$ ,

0, 5 / a_{0}

$0,5 / a_0$ ,

1 / a_{0}

$1 / a_0$ . Ini berarti bahwa tim pengembangan dapat mempertahankan jumlah kode yang ditulisnya untuk tahun ini, dengan seperempat, setengah, atau beban kerja penuh. Sebagai waktu hidup rata-rata kode, mari kita tetapkan nilai: 1, 2, dan 4 tahun. Memecahkan persamaan secara numerik, kami mendapatkan contoh perilaku fungsi

m u (t)

$\ mu (t)$ untuk beberapa kombinasi parameter

h, a_{0}, a_{1}

$h, a_0, a_1$ .
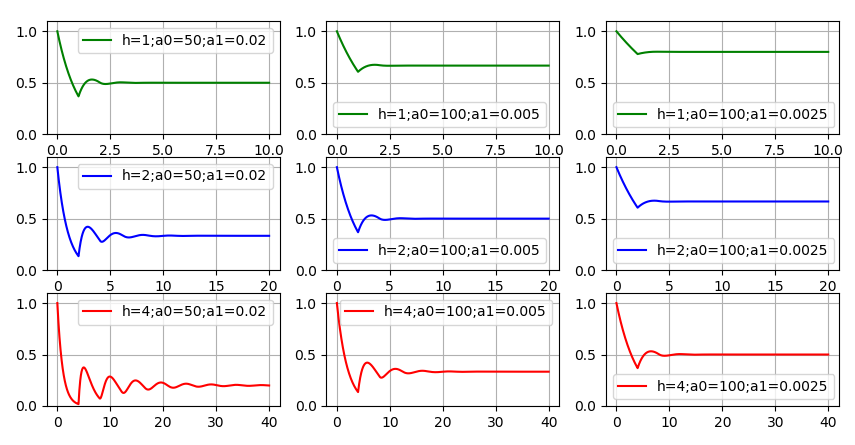
gambar

Fungsi Perilaku

m u (t)

$\ mu (t)$ dalam menghadapi kode penuaan telah berubah. Fungsi ini tidak lagi monoton, tetapi fluktuasi “tenang” seiring waktu, ada kecenderungan ke arah itu

m u (t)

$\ mu (t)$ ke beberapa nilai konstan. Grafik menunjukkan: semakin banyak

h

$h$ ,

a_{0}

$a_0$ dan

a_{1}

$a_1$ , yaitu, semakin lambat kode semakin tua, semakin cepat pengembangan kode baru terjadi dan semakin rendah kualitas kode, semakin sedikit sumber daya yang tersisa untuk pengembangan fungsionalitas baru. Ada keinginan untuk memberi setidaknya satu contoh

m u (t)

$\ mu (t)$ "Meringkuk" mendekati nol. Tetapi ini membutuhkan pemilihan indikator kualitas pembangunan yang sangat buruk dan kode yang lama. Bahkan di grafik kiri bawah, sejumlah besar sumber daya tetap untuk fungsi baru. Oleh karena itu, jawaban yang benar untuk pertanyaan pertama lebih cenderung seperti ini: secara teoritis - ya, itu mungkin; praktis - hampir tidak.

Pertanyaan yang tidak bisa dijawab:

Benarkah itu $\ mu (t)$ cenderung batas tertentu untuk $t \ hingga + \ infty$ untuk semua $a_0, a_1> 0$ ? Jika tidak untuk semua orang, lalu untuk apa?
Jika batas ada, maka bagaimana nilainya tergantung $a_0, a_1$ ?

Pertanyaan kedua. Dapatkah dukungan kode menyebabkan pertumbuhan jumlah programmer yang tidak terbatas?

Kami menunjukkan

q (t)

$q (t)$ jumlah programmer yang terlibat dalam pengembangan kode baru. Seperti di atas

y (t)

$y (t)$ - jumlah kode yang ditulis pada saat itu

t

$t$ . Lalu

f r a c d y (t) d t = a_{2} q (t); a_{2} i n m a t h b b R, a_{2} > 0.

$\ frac {dy (t)} {dt} = a_2 q (t); a_2 \ in \ mathbb {R}, a_2> 0.$

Biarkan dukungan kode sibuk

p (t)

$p (t)$ programmer. Penuaan kode C

p (t) = a_{3} (y (t) - y (t - h)); a_{3} i n m a t h b b R, a_{3} > 0.

$p (t) = a_3 (y (t) -y (t-h)); a_3 \ in \ mathbb {R}, a_3> 0.$

Dari mana

p (t) = a_{3} i n t_{t - h}^{t} f r a c d y (s) d s d s = a_{2} a_{3} i n t_{t - h}^{t} q (s) d s

$p (t) = a_3 \ int_ {t-h} ^ {t} \ frac {dy (s)} {ds} ds = a_2a_3 \ int_ {t-h} ^ tq (s) ds$

Jika

q (t) l e q C_{1}

$q (t) \ leq C_1$ lalu

p (t) l e q a_{1} a_{2} C_{1} h .

$p (t) \ leq a_1a_2C_1h.$

Dengan demikian, jawaban untuk pertanyaan kedua adalah negatif: jika jumlah pengembang kode baru terbatas, maka dalam konteks kode penuaan, dukungan tidak dapat menyebabkan peningkatan jumlah programmer yang tidak terbatas.

Kesimpulan

Model yang dipertimbangkan adalah model matematika "lunak" [2]. Mereka sangat sederhana. Namun demikian, ketergantungan hasil simulasi pada nilai parameter sesuai dengan yang diharapkan untuk sistem nyata, ini mendukung kecukupan model dan akurasi yang cukup untuk mendapatkan perkiraan kualitatif.

Referensi

1. Elsgolts L.E., Norkin S.B. Pengantar teori persamaan diferensial dengan argumen menyimpang. Moskow Rumah Penerbit "Sains". 1971.
2. Arnold V.I. Model matematika "Keras" dan "lunak". Moskow Rumah Penerbitan Center 2004

Berapa banyak programmer yang Anda butuhkan untuk mendukung kode yang ditulis sebelumnya?

Pertanyaan pertama. Bisakah mendukung "memakan" semua sumber daya pengembangan?

Pertanyaan kedua. Dapatkah dukungan kode menyebabkan pertumbuhan jumlah programmer yang tidak terbatas?

Kesimpulan

Referensi

More articles: