Model statistik baru tampaknya merusak asumsi yang telah lama diterima dari teori bilangan. Seberapa besar Anda bisa mempercayainya jika hanya bukti kuat yang benar-benar penting?
Baru-baru ini, empat peneliti telah datang dengan model yang membalikkan seluruh akal sehat bidang penelitian mereka. Mereka menggunakan data komputasi untuk menyarankan bahwa pandangan beberapa dekade yang berlaku tentang salah satu konsep dasar itu salah.
Dan ini bukan ahli biologi, ahli iklim atau fisikawan. Dalam bidang ilmiah mereka, model empiris tidak memiliki suara dalam kaitannya dengan kebenaran. Mereka adalah ahli matematika, perwakilan dari disiplin ilmu, yang mata uang standarnya - bukti logis yang tak terbantahkan - biasanya menyelamatkan mereka dari perdebatan yang memengaruhi area lain. Namun di sinilah mereka, dengan model mereka mengatakan bahwa mungkin sudah waktunya untuk merevisi beberapa ide yang sudah lama dimiliki.
Sebuah model yang
diterbitkan secara online pada tahun 2016 dan siap untuk muncul dalam Jurnal Masyarakat Matematika Eropa termasuk konsep matematika yang terhormat seperti pangkat persamaan aljabar. Rangking adalah ukuran yang berkaitan dengan berapa banyak solusi persamaan yang berhubungan dengan bilangan rasional, dan mana yang dengan irasional. Persamaan peringkat tinggi memiliki solusi yang lebih rasional dan lebih rumit.
Sejak awal abad ke-20, matematikawan telah tertarik pada pertanyaan apakah ada batasan pada ketinggian pangkat persamaan. Pada awalnya, hampir semua orang berpikir bahwa pembatasan itu harus ada. Tetapi pada tahun 1970-an, pendapat yang berlaku telah berubah - sebagian besar matematikawan mulai percaya bahwa peringkat itu tidak terbatas, yang berarti bahwa dimungkinkan untuk mendeteksi kurva dengan peringkat yang jauh lebih besar. Jadi itu terjadi, meskipun beberapa ahli matematika percaya bahwa tidak ada argumen yang kuat untuk mendukung pendapat ini.
“Orang-orang sangat otoriter tentang tidak adanya batasan. Namun, ketika Anda mulai memahami, ternyata bukti untuk ini sangat lemah, ”kata
Andrew Granville , ahli matematika di University of Montreal dan University College London.
Hari ini, bukti menunjukkan sebaliknya. Dua tahun setelah kemunculan model, dia meyakinkan banyak matematikawan bahwa pangkat persamaan aljabar dari jenis tertentu benar-benar terbatas. Namun, tidak semua orang menganggap model ini meyakinkan. Kurangnya kesepakatan menimbulkan pertanyaan yang tidak sering terkait dengan hasil matematika - berapa berat bukti empiris yang ada di area di mana hanya bukti yang penting yang penting?
"Tidak ada pembenaran matematis bahwa model ini adalah persis apa yang kita butuhkan," kata
Jennifer Park , seorang ahli matematika di Ohio University, co-penulis karya. "Selain itu, dari sudut pandang eksperimental, banyak hal yang berhasil."
Poin ke poin
Jika Anda diberi persamaan, Anda bisa menggambar kurva solusinya pada grafik. Matematikawan ingin tahu berapa banyak dari solusi ini yang rasional - mereka termasuk dalam tipe angka, yang dapat dinyatakan sebagai rasio dua bilangan bulat (1/2, -3 atau 4483/929).
Solusi rasional sulit ditemukan secara sistematis, tetapi matematikawan memiliki teknik yang bekerja dalam kondisi tertentu. Ambil persamaan x
2 + y
2 = 1. Grafik solusi untuk persamaan ini adalah lingkaran. Untuk menemukan semua titik rasional lingkaran, kita mulai dengan satu solusi pasti - katakanlah, dari titik di mana x = 1 dan y = 0. Kemudian gambar garis melalui titik ini yang memotong lingkaran di satu titik lain. Jika kemiringan garis kita rasional, maka titik persimpangan kedua juga akan menjadi solusi rasional. Dengan menarik garis, kami meningkatkan jumlah keputusan rasional dari satu menjadi dua.
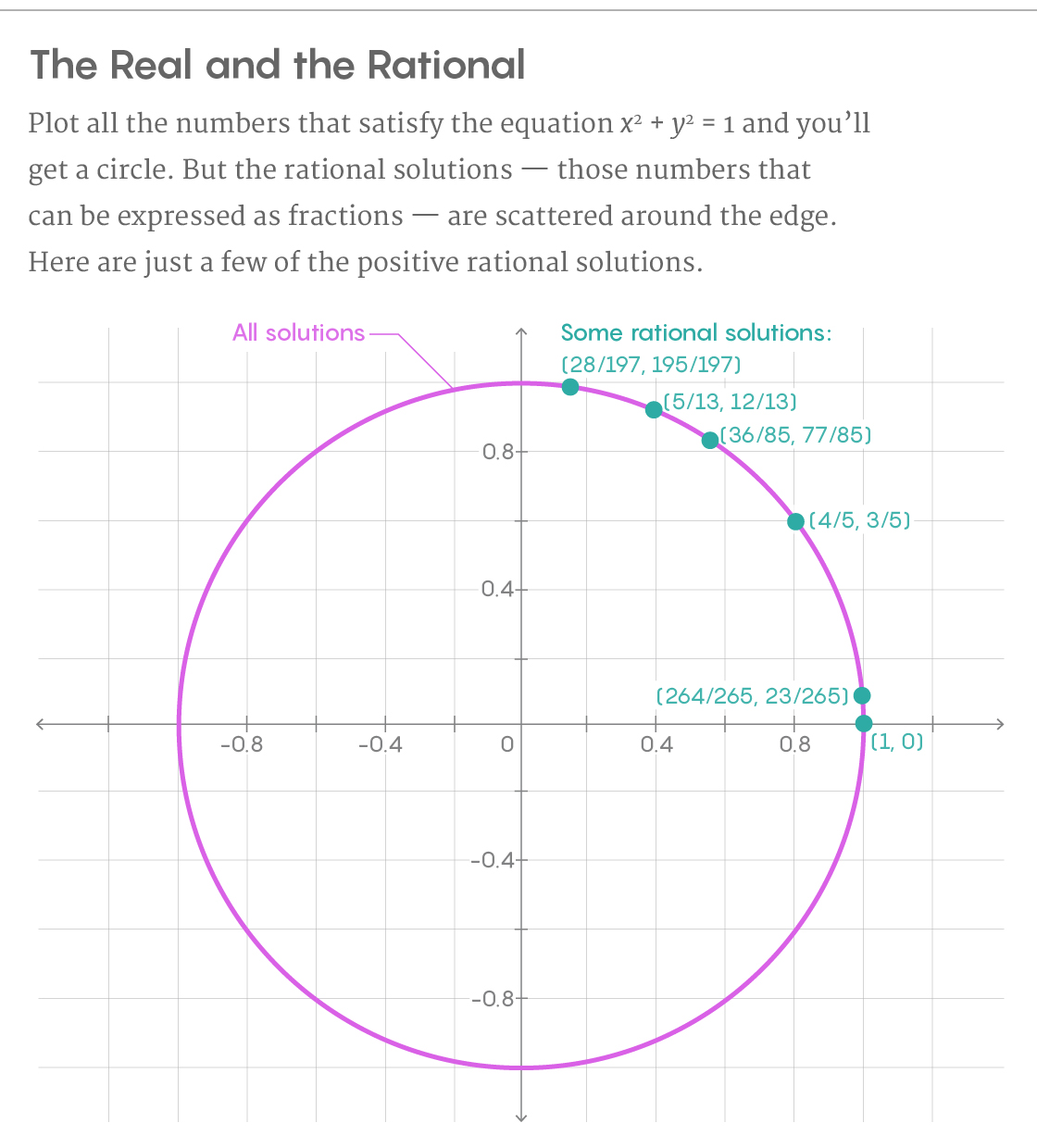
Dan tidak perlu berhenti di situ. Kami ulangi prosedur dengan menggambar garis lurus dengan kemiringan rasional lainnya melalui titik rasional kedua - memotong lingkaran pada titik rasional ketiga. Melanjutkan cara ini hingga tak terbatas, kita akhirnya akan menemukan semua titik rasional dari lingkaran, yang mana ada jumlah tak terbatas.
Dan dalam kasus lingkaran, Anda harus mulai dari satu titik saja, dan Anda dapat menemukan semuanya. Jumlah keputusan rasional yang perlu Anda ketahui di awal untuk menemukan yang lainnya dikenal sebagai pangkat kurva. Peringkat adalah cara yang rapi untuk menggambarkan sekumpulan keputusan rasional tanpa batas dalam satu angka. "Ini seperti cara terbaik untuk menggambarkan solusi rasional untuk kurva ini," kata
Björn Puunen , seorang ahli matematika di MIT, rekan penulis model, dengan Park,
John Voight dari Dartmouth College dan
Melanie Matchet Wood dari University of Wisconsin.
Lingkaran adalah persamaan kuadrat, atau persamaan derajat kedua ("derajat" berarti besarnya yang terbesar dari derajat syarat persamaan). Selama lebih dari seratus tahun, matematikawan telah mengetahui cara menemukan solusi rasional untuk persamaan tingkat kedua.
Jenis persamaan berikutnya adalah kurva eliptik, di mana ada variabel yang dinaikkan ke tingkat ketiga. Kurva elips ada di bidang penelitian matematika yang paling menarik. Mereka lebih rumit daripada persamaan orde kedua, sehingga mereka menarik untuk dipelajari, tetapi mereka tidak terlalu rumit. Prosedur yang diubah untuk menggambar garis lurus masih berlaku untuk kurva elips, tetapi berhenti bekerja dengan persamaan urutan keempat dan lebih tinggi.
Kurva berbentuk bulat panjang datang dalam peringkat yang berbeda. Dengan beberapa kurva elips, Anda bisa mulai dari satu titik rasional, menerapkan prosedur menggambar garis dan tidak menemukan semua solusi rasional. Anda mungkin perlu menambahkan titik rasional kedua yang tidak terkait dengan yang pertama. Dengan itu, Anda akan memulai prosedur baru untuk menggambar garis, dan Anda akan menemukan keseimbangan poin rasional. Kurva, untuk menemukan semua titik rasional yang perlu Anda ketahui dua poin rasional pada awalnya, memiliki peringkat sama dengan dua.
Tidak ada batasan yang terbukti pada ketinggian pangkat kurva elips. Semakin tinggi pangkat persamaan, semakin luas dan kompleks solusi himpunan kurva. "Pangkat itu entah bagaimana mengukur kompleksitas dari serangkaian keputusan," kata Puunen.
Namun demikian, pangkat ini menghindari upaya matematikawan untuk menggambarkannya dalam teori. Jika Anda diberi kurva elips, itu tidak akan memiliki hubungan yang jelas antara tampilannya dan apa peringkatnya. "Jika saya memiliki kurva elips, dan saya menyesuaikan koefisien sedikit, maka peringkatnya berubah secara radikal," kata Park. - Anda dapat mengubah koefisien dengan satu, dan pangkat akan melompat ke satu juta. Tidak ada yang tahu bagaimana jajarannya berperilaku. "
Kurangnya teori umum menyebabkan matematikawan mundur ke set kecil bukti yang mereka miliki untuk berspekulasi tentang adanya pembatasan peringkat. "Sudut pandangnya adalah bahwa tidak ada batasan pada peringkat, karena orang-orang selalu menemukan peringkat yang lebih tinggi," kata Granville. Pemegang rekor saat ini adalah kurva elips peringkat 28, ditemukan pada 2006 oleh Noam Elkis, seorang ahli matematika di Universitas Harvard.
Tapi kemudian model baru ini muncul, dan menyatakan bahwa itu hampir pasti akhir dari jalan.
Kejutan di sekitar 21
Untuk mempelajari fenomena yang terlalu kompleks atau tidak dapat diakses untuk penelitian langsung, para ilmuwan menggunakan model. Setelah membuat analog lubang hitam di laboratorium, mereka mungkin dapat mempelajari sesuatu tentang bagaimana lubang hitam yang sebenarnya berperilaku, tanpa harus berjalan di sepanjang tepi cakrawala peristiwa.
Matematikawan melakukan hal yang sama. Contoh yang baik adalah studi tentang bilangan prima. Matematikawan ingin mengetahui jawaban atas pertanyaan tentang
bilangan prima kembar - adakah jumlah pasangan bilangan prima tak terbatas yang berbeda dengan 2 (3 dan 5, 11 dan 13). Sebuah jawaban yang lengkap melampaui pengetahuan mereka, tetapi mereka menciptakan model yang memprediksi frekuensi angka kembar - dan jawabannya tampaknya bahwa mereka muncul dalam jumlah tak terbatas kali.
Model baru tidak secara langsung mempelajari kurva elips sendiri. Dia mengeksplorasi objek matematika seperti
inti matriks . Nukleus merujuk pada kurva elips, seperti tikus untuk manusia bukanlah hal yang sama, tetapi mereka lebih mudah dipelajari, dan diharapkan mereka cukup dekat untuk menarik kesimpulan tentang beberapa berdasarkan eksperimen pada orang lain. Secara khusus, kernel memiliki versi
peringkatnya sendiri . Setelah mempelajari distribusi pangkat inti - berapa banyak inti memiliki peringkat 1, berapa banyak inti memiliki peringkat 2, dan seterusnya - empat matematikawan berharap untuk mendapatkan gagasan tentang distribusi jajaran kurva elips. Bahkan, mereka bertaruh bahwa distribusi jajaran inti dan kurva eliptik mirip satu sama lain.
 Jennifer Park, Bjorn Puunen dan Melanie Wood
Jennifer Park, Bjorn Puunen dan Melanie Wood"Lompatan iman mulai berlaku," kata Park. "Kami berharap bahwa mungkin ada satu set objek matematika yang jauh lebih mudah dipahami dan memiliki distribusi peringkat yang sama dengan kurva elips."
Ketika keempat peneliti melakukan pekerjaan ini, sebagian besar matematikawan menganggap peringkat itu tidak terbatas. Namun, model tersebut menceritakan kisah yang berbeda. Dia mengatakan bahwa hanya ada jumlah terbatas dari kurva elips dengan peringkat lebih dari 21. Dan jika ada jumlah yang terbatas, maka salah satu dari mereka akan memiliki peringkat tertinggi - yang berarti bahwa peringkat tersebut masih memiliki batas atas. Ketika keempat matematikawan melihat ini, mereka menyadari bahwa mereka memiliki hasil hidup di tangan mereka.
"Prediksi ini tidak sesuai dengan apa yang diyakini semua orang, setidaknya apa yang mereka akui secara terbuka," kata Wood. "Tidak ada yang percaya bahwa peringkat bisa memiliki batasan."
Jika kepercayaan pada model membutuhkan langkah yang agak serius, maka ketika model melaporkan bahwa akal sehat salah, langkah yang lebih besar diperlukan. Namun, cukup banyak bukti yang mendukung hasil ini. Model ini didasarkan pada model sebelumnya yang dibuat oleh matematikawan lain yang telah mempelajari berbagai sifat kurva eliptik. Model-model itu telah teruji oleh waktu; beberapa prediksi ini bahkan telah terbukti.
"Tidak ada yang menyarankan mulai dari awal dan membuat model baru," kata Wood. "Pertanyaannya adalah bagaimana cara memperkaya model yang sudah ada yang sudah dipercaya orang."
Alasan lain untuk percaya pada model adalah bahwa nilai peringkat 21 tampaknya tidak menjadi batas yang sewenang-wenang. Sepuluh tahun sebelumnya, Granville menciptakan model lain, yang darinya juga diikuti bahwa seharusnya hanya ada sejumlah kecil kurva eliptik dengan peringkat di atas 21. Model Granville sama sekali tidak mirip dengan yang sekarang - dan fakta bahwa keduanya memberi peringkat 21 sebagai signifikan adalah sangat berbeda dengan kebetulan sederhana dari sudut pandang banyak ahli matematika.
"Kami memiliki dua model heuristik yang sama sekali berbeda dan keduanya memberikan nomor yang sama, 21 - itu mengejutkan orang," kata Park.
Mungkin alasan yang paling meyakinkan bahwa model tersebut tampaknya dapat dipercaya adalah kenyataan bahwa prediksi lainnya hampir sama persis dengan sifat-sifat kurva elips yang terbukti. Kesimpulan umum dari model - keberadaan sejumlah terbatas dari kurva eliptik dengan peringkat lebih dari 21 - berlaku untuk semua kurva eliptik. Namun, mereka memiliki keluarga tertentu, yang bagi banyak matematikawan telah menentukan batas-batas peringkat. Model ini juga memperkirakan nilai peringkat untuk banyak keluarga ini, dan prediksinya mirip, atau bahkan persis bertepatan dengan batas-batas yang telah ditentukan oleh ahli matematika.
"Perbatasan kami secara akurat memprediksi semua kasus yang dipelajari oleh orang lain," kata Park. "Orang-orang skeptis tentang laporan saya, tetapi ketika saya menyebutkan kebetulan lain, mereka sangat terkejut dengan hal ini."
Antara Bukti dan Bukti
Model ini memiliki banyak dukungan, tetapi tidak semua orang mempercayainya, dan itu ternyata salah. Skeptis yang paling penting adalah Noam Elkis, seorang ahli matematika Harvard yang menetapkan rekor peringkat untuk kurva elips. Dalam beberapa dekade sejak ia menjadi profesor penuh waktu termuda di Harvard, ia telah menerima beberapa hasil yang menunjukkan tidak adanya batas peringkat. "Pendapat saya tidak berubah untuk waktu yang lama - saya tidak berpikir bahwa kita berpengalaman dalam masalah ini untuk mendukung hipotesis ini atau itu," tulis Elkis kepada saya melalui surat.
Elkis percaya bahwa model tersebut mungkin tidak berfungsi dengan benar dalam banyak hal. Ini memperhitungkan kurva yang dipilih secara acak, atau kurva dalam beberapa hal adalah rata-rata. Namun, ada bukti, termasuk penelitian oleh Elkis sendiri, tentang kemungkinan keberadaan keluarga kurva eliptik, yang masing-masing mencakup jumlah tak terbatas kurva tersebut, yang perilakunya berbeda secara signifikan dari perilaku kurva khas. "Model heuristik berdasarkan perilaku yang diharapkan dari kurva acak mungkin tidak menceritakan keseluruhan cerita tentang perilaku ekstrem," tulis Elkis.
Bahkan salah satu penulis model tidak sepenuhnya yakin akan hal itu. "Saya akan mengatakan bahwa saya terbatas dalam peringkat seperti agnostik," kata Wood. Dia mengakui bahwa model itu mungkin salah karena alasan yang disuarakan oleh Elkis. Tetapi jika model tidak mengatasi tugas tersebut, maka karena tidak memperhitungkan beberapa sifat tersembunyi dan tak terduga dari kurva eliptik. "Pertanyaannya adalah: jika kamu tidak percaya pada peringkat yang terbatas, di mana model berhenti bekerja?" - kata Wood.
“Kemungkinan besar, mereka akan benar jika seseorang tidak datang dengan alasan cerdik mengapa mereka salah. Saya tidak tahu apakah ada alasan seperti itu atau tidak, ”kata Alexander Smith, seorang mahasiswa pascasarjana Harvard yang bekerja dengan Elkis dan mempelajari jajaran kurva elips.
Para penulis model tidak mengangkat maknanya menjadi dogma. Mereka tahu perbedaan antara bukti dan bukti, dan mereka mengerti bahwa tidak ada gunung dari yang pertama akan mengarah ke yang terakhir. Tetapi mereka percaya bahwa pekerjaan mereka, paling tidak, memberikan dasar yang masuk akal untuk merefleksikan konsep matematika dasar setelah seabad pemikiran sederhana.
"Mungkin menemukan kurva elips tingkat tinggi adalah tantangan bagi matematikawan," kata Park. Atau, mungkin, ahli matematika "harus mempertimbangkan kembali pendapat mereka tentang apa yang kami yakini, sebagai hipotesis populer."