Halo pengembara. Kita, sebagai pengembara dalam pikiran kita, dan penganalisa kondisi kita, harus memahami di mana itu baik, dan di mana sebaliknya, di mana tepatnya kita berada, dan saya ingin menarik pembaca untuk ini.
Bagaimana kita menyatukan rantai pemikiran, secara berurutan, dengan mengasumsikan kesimpulan dari setiap langkah, mengendalikan aliran kontrol dan keadaan sel dalam memori? Atau hanya dengan menggambarkan pernyataan masalah, beri tahu program tugas mana yang ingin Anda selesaikan, dan ini cukup untuk mengkompilasi semua program. Jangan mengubah pengkodean menjadi aliran perintah yang akan mengubah keadaan internal sistem, tetapi nyatakan prinsip sebagai konsep pengurutan, karena Anda tidak perlu membayangkan algoritma apa yang disembunyikan di sana, Anda hanya perlu mendapatkan data yang diurutkan. Bukanlah tidak berarti bahwa presiden Amerika dapat menyebutkan Bubble, dia mengungkapkan gagasan bahwa dia memahami sesuatu dalam pemrograman. Dia baru saja menemukan bahwa ada algoritma pengurutan, dan data dalam tabel di desktopnya, dengan sendirinya, tidak dapat berbaris, dalam beberapa cara ajaib, dalam urutan abjad.
Gagasan bahwa saya cenderung pada cara deklaratif untuk mengekspresikan pikiran, dan untuk mengekspresikan segala sesuatu dengan urutan perintah dan transisi di antara mereka, tampaknya kuno dan ketinggalan zaman, karena kakek kami melakukan ini, kakek menghubungkan kontak pada panel patch dan lampu berkedip, dan kami memiliki monitor dan pengenalan suara, karena pada tingkat evolusi ini Anda masih dapat berpikir tentang mengikuti perintah ... Menurut saya, jika Anda mengekspresikan program dalam bahasa yang logis, itu akan terlihat lebih dapat dimengerti, dan ini dapat dilakukan dalam teknologi, taruhan dibuat kembali di tahun 80-an.
Nah, pengantar diseret ....
Saya akan mencoba, sebagai permulaan, untuk menceritakan kembali mekanisme penyortiran cepat. Untuk mengurutkan daftar, Anda perlu membaginya menjadi dua sub-daftar dan menggabungkan satu sub-daftar yang diurutkan dengan sub-daftar yang diurutkan lainnya .
Operasi pemisahan harus dapat mengubah daftar menjadi dua sublists, salah satunya berisi semua elemen yang kurang mendasar, dan daftar kedua hanya berisi elemen besar. Mengekspresikan ini, hanya dua baris yang ditulis di Erlang:
qsort([])->[]; qsort([H|T])->qsort([X||X<-T,X<H])++[H|qsort([X||X<-T,X>=H])].
Ungkapan dari hasil proses pemikiran ini menarik bagi saya.
Lebih sulit untuk memberikan deskripsi tentang prinsip penyortiran dalam bentuk imperatif. Bagaimana mungkin ada keuntungan untuk metode pemrograman ini, dan kemudian Anda tidak menyebutnya, meskipun ada s-place-place, setidaknya fortran. Apakah karena javascript, dan semua tren fungsi lambda dalam standar baru semua bahasa, merupakan konfirmasi dari ketidaknyamanan algoritme.
Saya akan mencoba melakukan percobaan untuk memverifikasi manfaat dari satu pendekatan dan yang lain, untuk mengujinya. Saya akan mencoba menunjukkan bahwa catatan deklaratif dari definisi penyortiran dan catatan algoritmiknya dapat dibandingkan dalam hal kinerja dan menyimpulkan bagaimana merumuskan program dengan lebih tepat. Mungkin ini akan mendorong pemrograman ke rak melalui algoritma dan aliran perintah, sebagai pendekatan yang sudah ketinggalan zaman, yang sama sekali tidak relevan untuk digunakan, karena itu tidak kurang modis untuk mengekspresikan diri dalam Haskell atau dalam cross-section. Dan mungkin bukan hanya peri-tajam yang dapat memberikan program tampilan yang jelas dan kompak?
Saya akan menggunakan Python untuk demonstrasi, karena memiliki beberapa paradigma, dan ini bukan C ++ sama sekali dan tidak lagi cadel. Anda dapat menulis program yang jelas dalam paradigma yang berbeda:
Sortir 1
def qsort(S): if S==[]:return [] H,T=S[0],S[1:] return qsort([X for X in T if X<T])+[H]+qsort([X for X in T if X>=T])
Kata-kata dapat diucapkan seperti ini: pengurutan mengambil elemen pertama sebagai basis, dan kemudian semua yang lebih kecil diurutkan dan dihubungkan ke semua yang lebih besar, sebelum diurutkan .
Atau mungkin ungkapan seperti itu bekerja lebih cepat daripada menyortir yang ditulis dalam bentuk permutasi dari beberapa elemen di sekitarnya atau tidak. Apakah mungkin untuk mengungkapkan ini dengan lebih ringkas, dan tidak memerlukan banyak kata untuk ini. Cobalah untuk merumuskan dengan keras prinsip penyortiran berdasarkan gelembung dan menyampaikannya kepada Presiden Amerika Serikat , karena dia mendapatkan data suci ini, dia belajar tentang algoritme dan meletakkannya, misalnya, seperti ini: Untuk mengurutkan daftar, Anda perlu mengambil beberapa elemen, membandingkannya satu sama lain dan jika yang pertama lebih dari yang kedua, maka mereka harus ditukar, diatur ulang, dan kemudian Anda perlu mengulangi pencarian pasangan elemen tersebut dari awal daftar sampai permutasi selesai .
Ya, prinsip menyortir gelembung bahkan terdengar lebih lama dari versi pengurutan cepat, tetapi keunggulan kedua tidak hanya dalam singkatnya catatan, tetapi juga dalam kecepatannya, ekspresi dari pengurutan cepat yang sama yang dirumuskan oleh algoritma akankah ia lebih cepat daripada versi yang diungkapkan secara deklaratif? Mungkin kita perlu mengubah pandangan kita tentang pemrograman pengajaran, perlu bagaimana orang Jepang mencoba memperkenalkan pengajaran Prolog dan pemikiran terkait di sekolah. Anda dapat secara sistematis pindah ke jarak dari bahasa algoritmik ekspresi pikiran.
Sortir 2
Untuk mereproduksi ini, saya harus beralih ke literatur , ini adalah pernyataan dari Hoar , saya mencoba mengubahnya menjadi Python:
def quicksort(A, lo, hi): if lo < hi: p = partition(A, lo, hi) quicksort(A, lo, p - 1) quicksort(A, p + 1, hi) return A def partition(A, lo, hi): pivot = A[lo] i = lo - 1 j = hi + 1 while True do: i= i + 1 while A[i] < pivot do : j= j - 1 while A[j] > pivot if i >= j: return j A[i],A[j]=A[j],A[i]
Saya mengagumi pemikiran itu, sebuah siklus tak berujung diperlukan di sini, ia akan memasukkan pergi-yang ada)), ada beberapa pelawak.
Analisis
Sekarang mari kita membuat daftar panjang dan membuatnya mengurutkan berdasarkan kedua metode, dan memahami bagaimana mengekspresikan pikiran kita lebih cepat dan lebih efisien. Pendekatan mana yang lebih mudah dilakukan?
Membuat daftar angka acak sebagai masalah terpisah, beginilah caranya untuk diungkapkan:
def qsort(S): if S==[]:return [] H,T=S[0],S[1:] return qsort([X for X in T if X<H])+[H]+qsort([X for X in T if X>=H]) import random def test(len): list=[random.randint(-100, 100) for r in range(0,len)] from time import monotonic start = monotonic() slist=qsort(list) print('qsort='+str(monotonic() - start))
Berikut adalah pengukuran yang didapat:
>>> test(10000) qsort=0.046999999998661224 >>> test(10000) qsort=0.0629999999946449 >>> test(10000) qsort=0.046999999998661224 >>> test(100000) qsort=4.0789999999979045 >>> test(100000) qsort=3.6560000000026776 >>> test(100000) qsort=3.7340000000040163 >>>
Sekarang saya ulangi ini dalam formulasi algoritma:
def quicksort(A, lo, hi): if lo < hi: p = partition(A, lo, hi) quicksort(A, lo, p ) quicksort(A, p + 1, hi) return A def partition(A, lo, hi): pivot = A[lo] i = lo-1 j = hi+1 while True: while True: i=i+1 if(A[i]>=pivot) or (i>=hi): break while True: j=j-1 if(A[j]<=pivot) or (j<=lo): break if i >= j: return max(j,lo) A[i],A[j]=A[j],A[i] import random def test(len): list=[random.randint(-100, 100) for r in range(0,len)] from time import monotonic start = monotonic() slist=quicksort(list,0,len-1) print('quicksort='+str(monotonic() - start))
Saya harus bekerja mengubah contoh asli dari algoritma dari sumber kuno ke Wikipedia. Jadi ini: Anda perlu mengambil elemen pendukung dan mengatur elemen-elemen dalam subarray sehingga semuanya semakin sedikit di sebelah kiri, dan semakin banyak di sebelah kanan. Untuk melakukan ini, tukar sisi kiri dengan elemen kanan. Kami ulangi ini untuk setiap sublist dari elemen referensi dibagi dengan indeks, jika tidak ada yang berubah, kami selesai .
Total
Mari kita lihat apa perbedaan waktu untuk daftar yang sama, yang diurutkan berdasarkan dua metode secara bergantian. Kami akan melakukan 100 percobaan, dan membuat grafik:
import random def test(len): t1,t2=[],[] for n in range(1,100): list=[random.randint(-100, 100) for r in range(0,len)] list2=list[:] from time import monotonic start = monotonic() slist=qsort(list) t1+=[monotonic() - start]
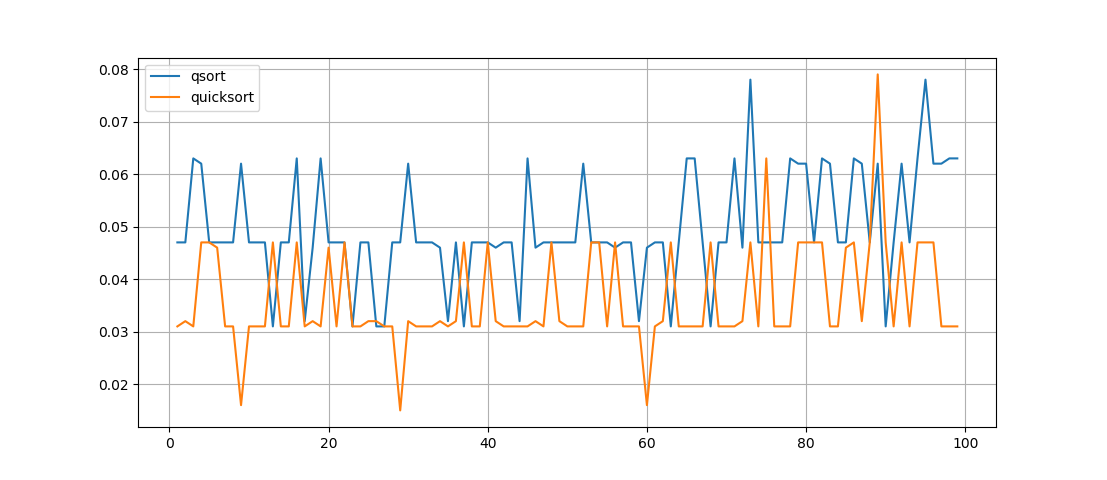
Apa yang bisa dilihat di sini - fungsi quicksort () bekerja lebih cepat , tetapi catatannya tidak begitu jelas, meskipun fungsinya rekursif, tetapi sama sekali tidak mudah untuk memahami pekerjaan permutasi yang dilakukan di dalamnya.
Nah, ungkapan pemikiran menyortir apa yang lebih sadar?
Dengan perbedaan kecil dalam kinerja, kami mendapatkan perbedaan volume dan kompleksitas kode tersebut.
Mungkin kebenaran sudah cukup untuk mempelajari bahasa imperatif, tetapi apa yang lebih menarik bagi Anda?
PS. Dan inilah Prolognya:
qsort([],[]). qsort([H|T],Res):- findall(X,(member(X,T),X<H),L1), findall(X,(member(X,T),X>=H),L2), qsort(L1,S1), qsort(L2,S2), append(S1,[H|S2],Res).