SDRAM DDR3 modern. Sumber: BY-SA / 4.0 oleh KjerishSelama kunjungan baru-baru ini ke
Computer History Museum di Mountain View, sampel kuno dari
memori ferit menarik perhatian saya.
Sumber: BY-SA / 3.0 oleh Konstantin LanzetSaya dengan cepat sampai pada kesimpulan bahwa saya tidak tahu bagaimana hal-hal seperti itu bekerja. Apakah cincinnya berputar (tidak), dan mengapa tiga kabel melewati masing-masing cincin (saya masih tidak mengerti cara kerjanya). Lebih penting lagi, saya menyadari bahwa saya memiliki sedikit sekali gagasan tentang cara kerja RAM dinamis modern!
Sumber: Memory Cycle Ulrich DrapperSaya sangat tertarik pada salah satu konsekuensi dari cara kerja RAM dinamis. Ternyata setiap bit data disimpan oleh muatan (atau ketidakhadirannya) pada kapasitor kecil dalam chip RAM. Tetapi kapasitor ini secara bertahap kehilangan muatannya seiring waktu. Untuk menghindari hilangnya data yang disimpan, data harus diperbarui secara berkala untuk mengembalikan biaya (jika ada) ke tingkat semula.
Proses pembaruan ini melibatkan membaca setiap bit dan kemudian menulisnya kembali. Selama "pembaruan" ini, memori sibuk dan tidak dapat melakukan operasi normal, seperti menulis atau menyimpan bit.
Ini mengganggu saya untuk waktu yang lama, dan saya bertanya-tanya ... apakah mungkin untuk melihat penundaan pembaruan di tingkat program?
Basis Pelatihan Peningkatan RAM Dinamis
Setiap DIMM terdiri dari "sel" dan "baris", "kolom", "sisi" dan / atau "peringkat".
Presentasi dari Universitas Utah ini menjelaskan nomenklatur tersebut. Konfigurasi memori komputer dapat diperiksa dengan perintah
decode-dimms . Berikut ini sebuah contoh:
$ decode-dimms
Ukuran 4096 MB
Bank x Baris x Kolom x Bit 8 x 15 x 10 x 64
Peringkat 2
Kami tidak perlu memahami seluruh skema DDR DIMM, kami ingin memahami operasi hanya satu sel yang menyimpan sedikit informasi. Lebih tepatnya, kami hanya tertarik pada proses pembaruan.
Pertimbangkan dua sumber:
Setiap bit dalam memori dinamis harus diperbarui: ini biasanya terjadi setiap 64 ms (yang disebut pembaruan statis). Ini adalah operasi yang agak mahal. Untuk menghindari satu perhentian besar setiap 64 ms, proses ini dibagi menjadi 8192 operasi pembaruan yang lebih kecil. Di masing-masing, pengontrol memori komputer mengirimkan perintah pembaruan ke chip DRAM. Setelah menerima instruksi, chip akan memperbarui 1/8192 sel. Jika Anda menghitung, maka 64 ms / 8192 = 7812,5 ns atau 7,81 μs. Ini berarti yang berikut:
- Perintah pembaruan dijalankan setiap 7812,5 ns. Ini disebut tREFI.
- Proses pembaruan dan pemulihan memerlukan waktu, sehingga chip dapat kembali melakukan operasi baca dan tulis normal. Yang disebut tRFC sama dengan 75 ns atau 120 ns (seperti dalam dokumentasi Micron yang disebutkan).
Jika memori panas (lebih dari 85 ° C), maka waktu penyimpanan data dalam memori berkurang, dan waktu pembaruan statis dikurangi setengahnya menjadi 32 ms. Dengan demikian, tREFI turun menjadi 3906,25 ns.
Chip memori biasa sibuk memperbarui untuk sebagian besar masa pakainya: dari 0,4% hingga 5%. Selain itu, chip memori bertanggung jawab atas bagian non-sepele dari konsumsi daya komputer biasa, dan sebagian besar daya ini dihabiskan untuk peningkatan.
Seluruh chip memori diblokir selama pembaruan. Artinya, setiap bit dalam memori dikunci selama lebih dari 75 ns setiap 7812 ns. Mari kita ukur.
Persiapan percobaan
Untuk mengukur operasi dengan akurasi nanosecond, Anda memerlukan siklus yang sangat ketat, mungkin dalam C. Sepertinya:
for (i = 0; i < ...; i++) {
Kode lengkap tersedia di GitHub.Kode ini sangat sederhana. Lakukan pembacaan memori. Kami membuang data dari cache CPU. Kami mengukur waktu.
(Catatan: dalam
percobaan kedua, saya mencoba menggunakan MOVNTDQA untuk memuat data, tetapi ini membutuhkan halaman memori non-cacheable khusus dan hak root).
Di komputer saya, program menampilkan data berikut:
# timestamp, waktu siklus
3101895733, 134
3101895865, 132
3101896002, 137
3101896134, 132
3101896268, 134
3101896403, 135
3101896762, 359
3101896901, 139
3101897038, 137
Biasanya, siklus dengan durasi sekitar 140 ns diperoleh, secara berkala waktu melonjak menjadi sekitar 360 ns. Terkadang hasil yang aneh muncul lebih dari 3200 ns.
Sayangnya, datanya terlalu berisik. Sangat sulit untuk melihat apakah ada penundaan nyata terkait dengan siklus pembaruan.
Transformasi Fourier Cepat
Pada titik tertentu saya sadar. Karena kami ingin menemukan acara dengan interval tetap, kami dapat mengirimkan data ke algoritma FFT (transformasi Fourier cepat), yang mendekripsi frekuensi utama.
Saya bukan orang pertama yang memikirkannya: Mark Seaborn dengan kerentanan terkenal
Rowhammer menerapkan teknik ini pada tahun 2015. Bahkan setelah melihat kode Mark, membuat FFT bekerja lebih sulit daripada yang saya harapkan. Tetapi pada akhirnya, saya mengumpulkan semua bagian.
Pertama, Anda perlu menyiapkan data. FFT membutuhkan input dengan interval pengambilan sampel yang konstan. Kami juga ingin memotong data untuk mengurangi kebisingan. Dengan coba-coba, saya menemukan bahwa hasil terbaik dicapai setelah pemrosesan awal data:
- Nilai-nilai kecil (kurang dari 1,8 rata-rata) dari iterasi loop terputus, diabaikan, dan diganti dengan nol. Kami benar-benar tidak ingin membuat kebisingan.
- Semua bacaan lainnya diganti oleh unit, karena amplitudo penundaan yang disebabkan oleh beberapa kebisingan benar-benar tidak penting bagi kami.
- Saya memilih interval sampling 100 ns, tetapi angka berapa pun hingga frekuensi Nyquist (frekuensi yang diharapkan ganda) akan berhasil .
- Data harus diambil sampelnya pada waktu yang tetap sebelum dikirim ke FFT. Semua metode pengambilan sampel yang masuk akal berfungsi dengan baik, saya memilih interpolasi linear dasar.
Algoritme adalah sesuatu seperti ini:
UNIT=100ns A = [(timestamp, loop_duration),...] p = 1 for curr_ts in frange(fist_ts, last_ts, UNIT): while not(A[p-1].timestamp <= curr_ts < A[p].timestamp): p += 1 v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0 v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0 v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp) B.append( v )
Yang pada data saya menghasilkan vektor yang agak membosankan seperti ini:
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...]
Namun, vektornya cukup besar, biasanya sekitar 200 ribu titik data. Dengan data tersebut, Anda dapat menggunakan FFT!
C = numpy.fft.fft(B) C = numpy.abs(C) F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)
Cukup sederhana, bukan? Ini menghasilkan dua vektor:
- C berisi sejumlah komponen frekuensi yang kompleks. Kami tidak tertarik dengan bilangan kompleks, dan Anda dapat memuluskannya dengan perintah
abs() . - F berisi label, yang rentang frekuensi terletak di tempat vektor C. Kami menormalkan eksponen ke hertz dengan mengalikannya dengan frekuensi sampling dari vektor input.
Hasilnya dapat diplot pada grafik:
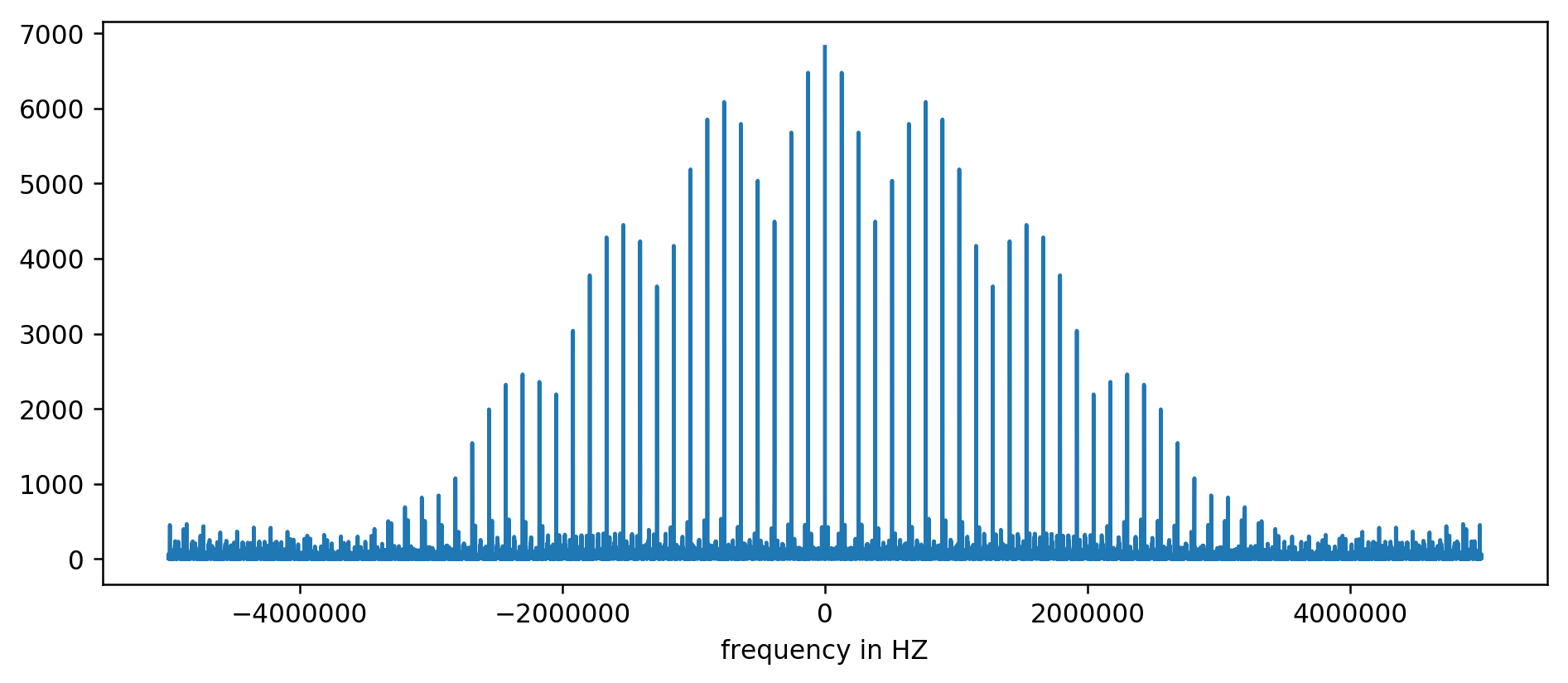
Sumbu Y tanpa unit, karena kami menormalkan waktu tunda. Meskipun demikian, semburan terlihat jelas di beberapa rentang frekuensi tetap. Mari kita pertimbangkan mereka lebih dekat:
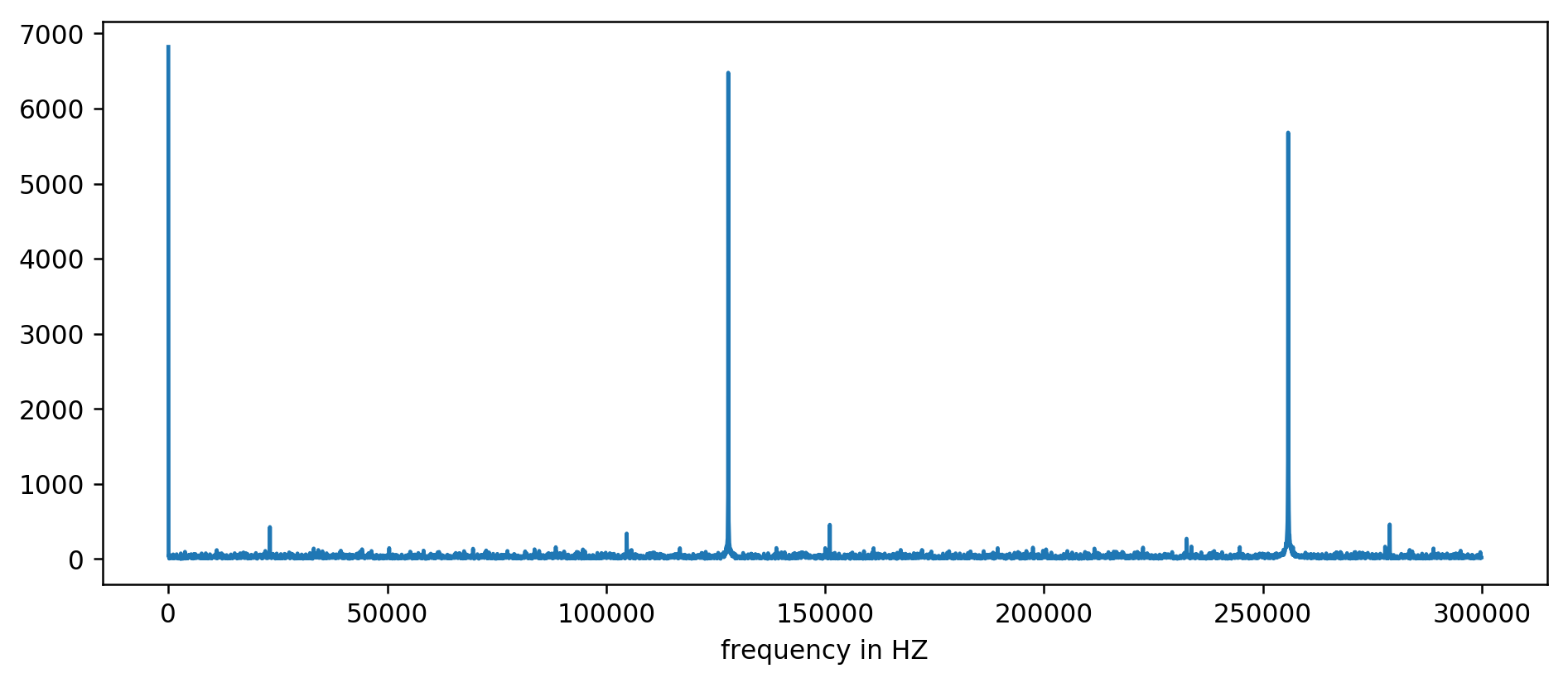
Kami jelas melihat tiga puncak pertama. Setelah sedikit aritmatika yang tidak ekspresif, termasuk membaca pemfilteran setidaknya sepuluh kali rata-rata, Anda dapat mengekstrak frekuensi basis:
127850.0
127900.0
127950.0
255700.0
255750.0
255800.0
255850.0
255900.0
255950.0
383600.0
383650.0
Kami menganggap: 1000000000 (ns / s) / 127900 (Hz) = 7818,6 ns
Hore! Lompatan pertama dalam frekuensi benar-benar apa yang kita cari, dan itu benar-benar berkorelasi dengan waktu pembaruan.
Puncak yang tersisa pada 256 kHz, 384 kHz, 512 kHz adalah harmonik yang disebut yang merupakan kelipatan dari frekuensi dasar kami yaitu 128 kHz. Ini adalah efek samping yang sepenuhnya diantisipasi dari
menerapkan FFT ke sesuatu seperti gelombang persegi .
Untuk memfasilitasi percobaan, kami membuat
versi untuk baris perintah . Anda dapat menjalankan kode sendiri. Berikut adalah contoh peluncuran di server saya:
~ / 2018-11-memory-refresh $ make
gcc -msse4.1 -ggdb -O3 -Wall -Wextra ukur-dram.c -o ukur-dram
./measure-dram | python3 ./analyze-dram.py
[*] Memverifikasi ASLR: main = 0x555555554890 tumpukan = 0x7fffffefe2ec
[] Fakta menyenangkan. Saya melakukan 40663553 clock_gettime () per detik
[*] Mengukur waktu MOVQ + CLFLUSH. Menjalankan 131072 iterasi.
[*] Menulis data
[*] Input data: min = 117 rata-rata = 176 med = 167 maks = 8172 item = 131072
[*] Kisaran cutoff 212-inf
[] 127849 item di bawah cutoff, 0 item di atas cutoff, 3223 item tidak nol
[*] Menjalankan FFT
[*] Frekuensi teratas di atas 2kHz di bawah 250kHz memiliki besaran 7716
[+] Paku frekuensi teratas di atas 2kHZ berada di:
127906Hz 7716
255813Hz 7947
383720Hz 7460
511626Hz 7141
Saya harus akui, kodenya tidak sepenuhnya stabil. Jika terjadi masalah, disarankan untuk menonaktifkan Turbo Boost, penskalaan frekuensi CPU, dan pengoptimalan untuk kinerja.
Kesimpulan
Ada dua kesimpulan utama dari karya ini.
Kami melihat bahwa data tingkat rendah cukup sulit untuk dianalisis dan tampaknya agak bising. Alih-alih mengevaluasi dengan mata telanjang, Anda selalu dapat menggunakan FFT tua yang baik. Dalam persiapan data, perlu, dalam arti tertentu, untuk angan-angan.
Yang paling penting, kami telah menunjukkan bahwa seringkali mungkin untuk mengukur perilaku perangkat keras yang halus dari proses sederhana di ruang pengguna. Pemikiran semacam ini mengarah pada penemuan
kerentanan Rowhammer yang asli , itu diimplementasikan dalam serangan Meltdown / Spectre dan sekali lagi ditunjukkan dalam
reinkarnasi Rowhammer baru-baru ini
untuk memori ECC .
Masih banyak di luar ruang lingkup artikel ini. Kami nyaris tidak menyentuh operasi internal subsistem memori. Untuk bacaan lebih lanjut, saya sarankan:
Akhirnya, berikut ini adalah deskripsi yang baik dari memori ferit lama: