Implementasi Praktis dari Switching Generator Menggunakan Verilog HDL

Abstrak

Register shift umpan balik linier adalah alat yang sangat baik untuk mengimplementasikan generator bit pseudo acak dalam perangkat keras; mereka menghambat struktur elektronik yang sederhana dan efisien. Selanjutnya, mereka mampu menghasilkan urutan output dengan periode besar dan sifat statistik yang baik. Namun, LFSR standar tidak aman secara kriptografi, karena urutan output dapat diprediksi secara unik mengingat sejumlah kecil bit aliran kunci menggunakan algoritma Berlekamp-Massey. Beberapa metode telah diusulkan untuk menghancurkan linearitas yang melekat dalam desain LFSR. Metode ini termasuk generator kombinasi nonlinier, generator filter nonlinier, dan generator yang dikendalikan jam. Namun demikian, mereka tetap rentan terhadap banyak serangan seperti serangan saluran samping dan serangan aljabar. Pada 2015, sebuah generator baru yang dikendalikan clocked, yang disebut generator switching, diusulkan. Generator baru ini telah terbukti tahan terhadap serangan aljabar dan serangan saluran samping, sambil menjaga efisiensi dan persyaratan keamanan. Dalam proyek ini, kami menyajikan desain generator switching menggunakan Verilog HDL.

Pengantar dan Latar Belakang Sejarah

Sejarah pembuatan nomor acak semu dalam perangkat keras sangat terkait dengan pengembangan stream cipher. Stream cipher adalah cipher yang mengenkripsi karakter teks biasa secara individual (biasanya sedikit demi sedikit), berbeda dengan memblokir cipher, yang mengenkripsi teks biasa dalam blok besar (64 bit atau lebih). Banyak arsitektur stream cipher memerlukan generator aliran kunci, yang merupakan generator bit acak semu yang benihnya adalah kunci enkripsi. Untuk setiap bit teks biasa, bit teks sandi yang sesuai dihitung sebagai beberapa fungsi yang dapat dikembalikan (biasanya gerbang xor) dari bit teks biasa dan bit aliran kunci yang sesuai. Oleh karena itu, merancang generator aliran kunci yang aman dan efisien sangat penting untuk operasi stream cipher.


Salah satu alat yang berguna untuk membangun generator aliran utama adalah register shift umpan balik linier. Mereka dapat dibangun dengan mudah menggunakan komponen elektronik dasar, dan dapat diprogram hanya pada perangkat logika yang dapat diprogram. Selain itu, karena strukturnya yang sederhana, LFSR dapat dimodelkan dan dianalisis secara matematis, yang telah menghasilkan pengetahuan dan hasil yang luas mengenai mereka. Urutan output dari LFSR yang dibangun dengan benar memiliki panjang eksponensial dan sifat statistik yang baik seperti kompleksitas linear yang besar.


Terlepas dari sifat statistik LFSR yang baik, ia tidak dapat digunakan sebagai generator aliran utama dalam bentuk standar karena sifat liniernya. Jika seorang penyerang berhasil mengetahui $$$2L$bit stream key berturut-turut, maka urutan output dapat diprediksi secara unik dan efisien menggunakan algoritma Berlekamp-Massey, di mana $$$L$adalah jumlah register. Banyak cara berbeda untuk menghancurkan linieritas yang melekat dalam urutan output LFSR telah diusulkan:

• Menggunakan beberapa LFSR dan fungsi kombinasi non-linear dari outputnya (generator kombinasi non-linear).
• Menghasilkan urutan output sebagai beberapa fungsi non-linear dari status LFSR (generator filter non-linear).
• Pencatatan jam kerja LFSR yang tidak teratur (generator yang dikendalikan jam).

Namun, semua desain ini tetap rentan terhadap serangan seperti serangan aljabar dan saluran samping. Setelah tahun 2000, ini bukan lagi masalah kritis, karena block cipher Rijndael diusulkan dan terpilih sebagai Advanced Encryption Standard (AES). AES mampu beroperasi dalam mode stream cipher dan memenuhi semua standar industri untuk stream cipher. Selanjutnya, dengan munculnya kekuatan komputasi, AES dapat digunakan pada berbagai platform. Ini telah menyebabkan penurunan yang signifikan dalam aplikasi stream cipher.


Adi Shamir mempresentasikan kuliah yang diundang di State of the Art in Stream Ciphers 2004 dan Asiacrypt 2004 berjudul "Stream Ciphers: Dead or Alive?". Dalam presentasinya, ia menyarankan agar stream cipher dapat bertahan dalam aplikasi berikut:

• Aplikasi berorientasi perangkat lunak dengan kecepatan sangat tinggi (mis. Router).
• Aplikasi yang berorientasi pada perangkat keras dengan tapak yang sangat kecil (mis. Kartu pintar).

Salah satu proposal terbaru untuk generator aliran utama adalah switching generator. Ia diklaim tahan terhadap serangan aljabar dan saluran samping, sambil mempertahankan efisiensi dan kecepatan operasi.


Dalam proyek ini, kami akan menyajikan desain generator switching dalam perangkat keras, menggunakan Verilog HDL. Pertama, kami menyajikan dua bentuk umum LFSRs, Fibonacci LFSRs dan Galois LFSRs. Selanjutnya, kami menyajikan presentasi matematika LFSR. Kami kemudian akan menyajikan generator switching seperti yang diperkenalkan oleh. Akhirnya, kami menghadirkan desain Verilog dari generator switching.

Register Shift Umpan Balik Linier

Register shift umpan balik linier adalah sirkuit yang terdiri dari daftar register linear (juga disebut elemen penundaan) dan seperangkat koneksi yang telah ditentukan di antara mereka. Sinyal jam global (tunggal) mengontrol aliran data di dalam LFSR. Dua jenis LFSR yang paling umum digunakan adalah Fibonacci LFSRs dan Galois LFSRs; menunda hanya dalam bentuk koneksi. Seperti yang akan kita lihat nanti di bagian model matematika, ada banyak kesamaan antara Fibonacci dan arsitektur Galois, lebih memilih satu daripada yang lain adalah aplikasi spesifik.


Melalui artikel ini, kami mengasumsikan penghitung waktu global hipotetis mulai dari $$$0$dan meningkat sebesar $$$1$setelah setiap tepi positif dari siklus clock global.

Daftar

Register adalah elemen logika yang mampu menyimpan satu bit data, yang disebut state. Ini memiliki dua jalur input: jalur data satu bit dan jalur sinyal jam. Ini memiliki output satu bit yang selalu sama dengan keadaan internal. Di setiap sisi positif dari input jam, input data ditetapkan ke negara, jika tidak negara tidak akan berubah. Mari kita nyatakan status register $$$S$pada waktu $$$t$sebagai $$$\ mathop S \ nolimits ^ t$.

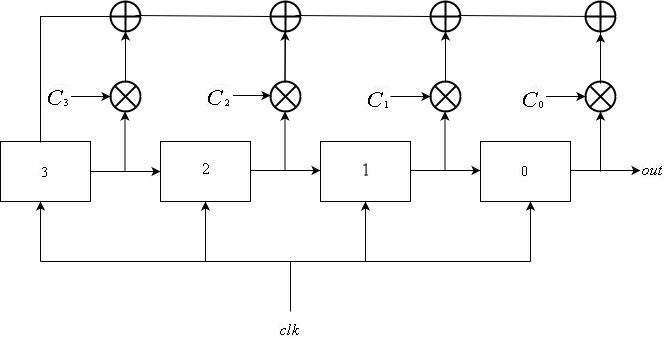
Fibonacci lfsrs

Fibonacci LFSR terdiri dari $$$L$register yang disebutkan dari $$$0$untuk $$$L-1$, semua terhubung ke sinyal clock yang sama. Masukan dari register $$$i$adalah output dari register $$$i + 1$untuk $$$0 \ le i \ le L-2$. Masukan umpan balik untuk register $$$L-1$adalah jumlah xor dari beberapa subset register. Pembaruan register dapat dijelaskan secara matematis sebagai berikut:

$$

$$\ mathop S \ nolimits_i ^ t = \ kiri \ {\ begin {array} {l} \ mathop S \ nolimits_ {i + 1} ^ {t-1} {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ rm {if} \ \} 0 \ le i \ le L-2 \\ \ mathop \ bigoplus \ limit_ {j = 1} ^ k \ mathop S \ nolimits_j ^ {t-1} \ otimes \ mathop C \ nolimits_j {\ \ \ \ \ rm {if} \ \} i = L-1 \ end {array} \ benar.$$

dimana $$$C_j = 1$jika mendaftar $$$j$termasuk dalam umpan balik dan $$$0$jika tidak.

Urutan output diperoleh dari register $$$0$. Artinya, urutan outputnya $$$\ mathop {\ left \ {{\ mathop S \ nolimits_0 ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

LFSR Galois

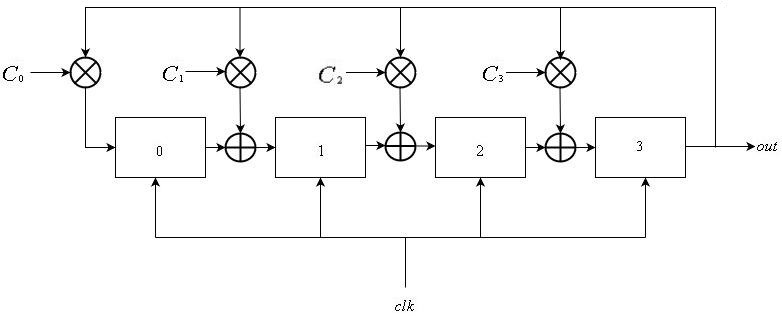
LFSR Galois juga terdiri dari daftar linear $$$L$register yang disebutkan dari $$$0$untuk $$$L-1$, semua berbagi sinyal jam global. Masukan dari register $$$i$adalah output dari register $$$i-1$untuk $$$1 \ le i \ le L-1$. Untuk sebagian sub register, inputnya di-xored dengan output register $$$L-1$. Ini dapat dinyatakan sebagai:

$$

$$\ mathop S \ nolimits_i ^ t = \ kiri \ {\ begin {array} {l} \ mathop S \ nolimits_ {i-1} ^ {t-1} \ oplus \ mathop S \ nolimits_ {L-1} ^ {t-1} \ otimes \ mathop C \ nolimits_i {\ rm {\ \ \ jika if \}}} 1 \ le i \ le L-1 \\ \ mathop S \ nolimits_ {L-1} ^ {t- 1} \ otimes \ mathop C \ nolimits_0 {\ rm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ jika \ \}} i = 0 \ end {array} \ benar.$$

dimana $$$C_i = 1$jika input register $$$i$xored dengan output register $$$L-1$.


Dengan cara yang mirip dengan Fibonacci LFSRs, urutan output didefinisikan sebagai $$$\ mathop {\ left \ {{\ mathop S \ nolimits_ {L-1} ^ i} \ kanan \}} \ nolimits_ {i \ ge 0}$ .

Perbandingan Antara Fibonacci dan Desain Galois

Ada korespondensi langsung antara Fibonacci dan Galois LFSR dalam arti matematis, seperti yang akan kita lihat di bagian selanjutnya. Namun, ada dua keuntungan penting menggunakan desain Galois:

• Dalam implementasi perangkat lunak, itu tidak memerlukan $$$L$pemeriksaan paritas bit, yang menambahkan faktor kompleksitas logaritmik.
• Dalam implementasi perangkat keras, itu hanya membutuhkan gerbang input-dua, yang keterlambatan propagasinya kurang signifikan dibandingkan dengan gerbang input-ganda yang digunakan dalam desain Fibonacci.

Dalam proyek kami, kami mempertimbangkan perumusan matriks LFSR, sehingga kedua arsitektur dapat dipertukarkan.

Model Matematika LFSR

Di bagian berikut, kecuali dinyatakan sebaliknya, kami mengasumsikan bahwa semua perhitungan dilakukan di bawah bidang Galois $$$Gf \ kiri (2 \ kanan)$. Artinya, semua operasi dihitung modulo $$$2$. Implementasi lain dari konvensi ini adalah bahwa semua multiplikasi adalah logis dan gerbang, dan semua penjumlahan adalah gerbang xor.


Pertimbangkan kondisi semua $$$L$register LFSR suatu saat $$$t$; ini dapat direpresentasikan sebagai vektor dari $$${\ left \ {{0,1} \ right \} ^ L}$ :

$$

$${S ^ t} = \ kiri ({\ mathop S \ nolimits_0 ^ t; \ mathop S \ nolimits_1 ^ t; \ ldots; \ mathop S \ nolimits_ {L-1} ^ t} \ kanan)$$

Kami menyatakan vektor ini sebagai keadaan LFSR. Perhatikan bahwa paling banyak ada $$${2 ^ L}$kemungkinan status untuk $$$L$daftar LFSR. Juga catat bahwa jika suatu LFSR ingin mencapai status semua-nol, ia tidak dapat mencapai kondisi lainnya. Karena itu kami katakan ada $$$2 ^ L-1$non-sepele dari LFSR.


Pertimbangkan transformasi linear berikut:

$$

$$F = \ kiri ({\ begin {array} {* {20} {c}} 0 & 1 & \ cdots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & 1 \\ {\ mathop C \ nolimits_0} & {\ mathop C \ nolimits_1} & \ cdots & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ kanan)$$

Mengingat itu $$$\ mathop S \ nolimits ^ t$adalah keadaan Fibonacci LFSR, dapat diamati itu

$$

$$F \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

Jika $$$\ mathop S \ nolimits ^ t$adalah keadaan LFSR Galois, maka pertimbangkan tranformasi $$$G$:

$$

$$G = \ kiri ({\ begin {array} {* {20} {c}} 0 & \ cdots & 0 & {\ mathop C \ nolimits_0} \\ 1 & \ cdots & 0 & {\ mathop C \ nolimits_1} \\ \ vdots & \ ddots & \ vdots & \ vdots \\ 0 & \ cdots & 1 & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ kanan)$$

Dalam hal ini, kami punya

$$

$$G \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

Representasi matriks LFSRs bisa fleksibel ketika berhadapan dengan pembaruan berulang, karena mereka dapat ditafsirkan sebagai produk matriks sederhana. Dapat diamati itu $$$F = {G ^ T}$. Fakta ini menunjukkan banyak kesamaan antara desain Fibonacci dan Galois jika mereka dipandang sebagai transformasi linear dari $$${\ left \ {{0,1} \ right \} ^ N}$ untuk $$${\ left \ {{0,1} \ right \} ^ N}$ .


Mengalikan vektor keadaan beberapa LFSR dengan matriks (tipe Fiboancci atau Galois) dikenal sebagai pencatatan waktu atau pembaruan LFSR.

Generator switching

Switching Generator adalah generator yang dikendalikan jam yang diusulkan pada tahun 2015. Itu terbukti memiliki ketahanan terhadap serangan aljabar dan saluran samping. Pada bagian ini, kami akan menyajikan desain generator switching, sebagaimana ditentukan oleh para penemunya.

Struktur dasar

Generator switching terdiri dari dua LFSR: LFSR kontrol $$$A$panjangnya $$$N$dan LFSR data $$$B$panjangnya $$$M$. Kontrol LFSR diperbarui seperti yang dijelaskan sebelumnya. Namun, data LFSR diperbarui menggunakan salah satu dari dua matriks yang mungkin, $$$\ mathop M \ nolimits_1 ^ i$atau $$$\ mathop M \ nolimits_2 ^ j$dimana $$${M_1}, {M_2}$adalah matriks pendamping dari beberapa polinomial primitif. Memilih satu matriks dari yang lain ditentukan oleh output sinyal dari LFSR kontrol. Proses ini dapat digambarkan sebagai berikut:

$$

$$\ mathop B \ nolimits ^ t = \ kiri \ {\ begin {array} {l} \ mathop M \ nolimits_1 ^ i \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ jika \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 0 \\ \ mathop M \ nolimits_2 ^ j \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ jika \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 1 \ end {array} \ benar.$$

Output dari generator switching adalah output dari LFSR $$$B$. Perhatikan bahwa kami berasumsi itu $$$A$adalah LFSR Galois. Ini juga bisa menjadi Fibonacci LFSR.


Integer $$$i, j$Disebut indeks pengalihan.

Benih

Ingatlah bahwa LFSR dapat melakukan iterasi paling banyak $$${2 ^ L} -1$negara non-sepele sebelum meninjau kembali negara sebelumnya. Karena matriks $$${M_1}, {M_2}$adalah matriks transformasi LFSRs, kita dapat menyimpulkan bahwa integer $$$i, j$paling banyak $$$2 ^ M-1$sebelum matriks mulai diulang.


Benih untuk generator switching adalah $$$N + 3M$bit, mewakili status awal LFSRs $$$A$dan $$$B$dan kekuatan bilangan bulat $$$i, j$. Perhatikan bahwa matriks $$${M_1}, {M_2}$diperbaiki sepanjang implementasi dan tidak termasuk dalam benih.

Desain Verilog

Pada bagian ini, kami akan memperkenalkan desain generator switching menggunakan Verilog HDL. Kami akan menyajikan setiap desain modul secara bottom up. Pada akhirnya, kami memperkenalkan modul generator switching.


Dalam desain kami, kami mencoba menjaga agar komponen sinkron tetap minimum. Satu-satunya komponen yang dikendalikan jam adalah LFSRs $$$A, B$.


Matriks dan operasi vektor dapat diimplementasikan dalam sejumlah metode yang berbeda, bervariasi dalam konsumsi unit logika, unit memori dan kompleksitas prosedural. Dalam desain kami, kami menghilangkan kebutuhan untuk blok prosedural, dan menggunakan elemen-elemen logika secara maksimal.


Semua matriks dalam modul berikut diindeks mulai dari $$$0$kiri ke kanan, lalu atas ke bawah.


Perhatikan juga bahwa semua modul memiliki ukuran parameter; ini untuk keperluan debugging. Dalam implementasi aktual, semua ukuran diperbaiki.

Multiplexer

Ini adalah modul yang menerapkan 2 to 1 $$$N$multiplexer -bit. Modul ini memiliki dua $$$N$jalur input-bit, satu jalur pemilih 1-bit, dan $$$N$garis output-bit. Jika input pemilih adalah $$$0$maka output diatur ke jalur input pertama, jika tidak diatur ke yang kedua.


Modul multiplexer

Transformasi vektor

Modul ini mengimplementasikan transformasi linear pada vektor. Menerima sebagai input dan $$$N \ kali N$matriks transformasi dan $$$N$-bit vektor. Ini mengeluarkan produk matriks-vektor dari inputnya.


Setiap bit dalam vektor output adalah hasil dari sebuah $$$N$-bit xor gate, mengambil sebagai input hasil dari $$$N$-bit bitwise dan dari vektor input dan baris matriks yang sesuai. Artinya, setiap bit output bawaan untuk input, dan tidak ada blok prosedural yang diperlukan.


Tepat $$$N ^ 2$dua input dan gerbang digunakan, bersama dengan $$$N$$$$N$-input gerbang xor.


Modul Transformasi Vektor

Identitas

Modul ini tidak menerima input. Ini $$$N \ kali N$-bit output diinisialisasi ke $$$N$matriks identitas. Modul semacam itu dideklarasikan demi kenyamanan, sehingga kita tidak perlu menginisialisasi vektor register global untuk setiap ukuran yang berbeda.


Modul Matriks Identitas

Transpose

Modul ini menerima $$$N \ kali N$matriks dan output transposnya. Baik elemen logis maupun memori tidak digunakan dalam modul ini, outputnya hanyalah permutasi dari inputnya
.

Modul Transpose Matriks

Penggandaan Matriks

Ini adalah modul yang menerapkan perkalian matriks-matriks. Ia menerima dua $$$N \ kali N$matriks sebagai input, dan mengeluarkan produk matriks-matriks mereka.


Modul ini berisi turunan dari modul transpose matriks. Ini memungkinkan untuk menetapkan indeks berurutan ke kolom dalam matriks input kedua. Setiap entri dalam matriks output kemudian ditugaskan untuk output dari suatu $$$N$-input gerbang xor, yang inputnya adalah bitwise dan dari baris yang sesuai dari matriks pertama dan kolom dari yang kedua.


Tepat $$$N ^ 3$dua input dan gerbang dan $$$N ^ 2$$$$N$-input xor digunakan dalam implementasi ini.


Modul Penggandaan Matriks

Eksponen Matriks

Modul ini meningkatkan matriks ke daya integer. Menerima sebagai input dan $$$N \ kali N$matriks dan a $$$K$bilangan bulat-bit. Keluarannya adalah matriks yang dinaikkan ke daya integer yang ditentukan.


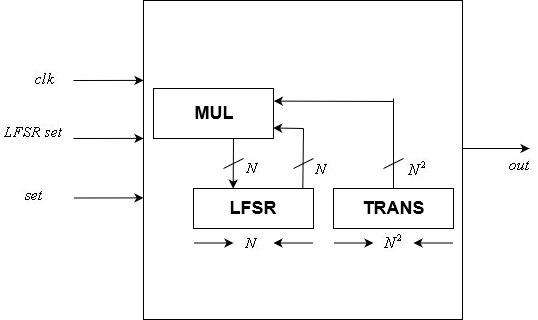
Modul Eksponen Matriks

Unit kontrol

Modul ini mengimplementasikan $$$N$-bit control LFSR. Ini adalah salah satu dari dua modul yang dikendalikan jam dalam desain kami.


Ini termasuk statis $$$N \ kali N$Matriks transformasi LFSR dan variabel $$$N$-bit state. Inputnya termasuk jam, sebuah $$$N$-bit state reset, dan sinyal reset. Keluarannya adalah bit tunggal, yang merupakan bit terakhir dari LFSR.


Setelah setiap tepi positif sinyal jam, keadaan diperbarui sesuai dengan matriks transformasi menggunakan modul multiplikasi matriks-vektor. Reset negara ditetapkan ke status internal setelah setiap sisi positif dari sinyal reset.





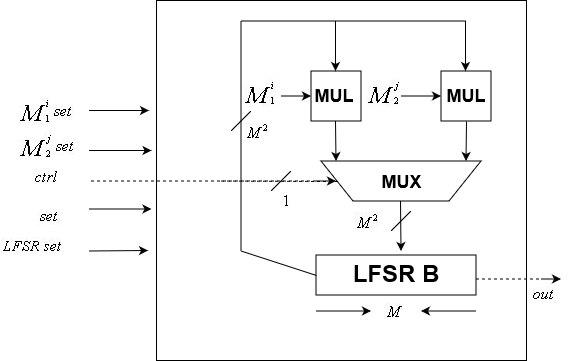
Modul unit kontrol

Unit data

itu $$$N$data LFSR diimplementasikan menggunakan modul ini. Seperti modul unit kontrol, ini dikendalikan oleh jam


Modul ini mencakup dua $$$N \ kali N$matriks transformasi dan $$$N$-bit LFSR state. Ini menerima sebagai input sinyal jam, sinyal kontrol, dan $$$N$-bit LFSR mengatur ulang negara, dua $$$N \ kali N$transformasi matriks ulang, dan sinyal reset. Ini memiliki output satu bit, bit terakhir dari LFSR internal.


Perhatikan bahwa karena benih dapat diubah, maka matriks transformasi juga dapat diubah, tidak seperti unit kontrol yang matriks transformasi jika diperbaiki.




\ Unit Data

Generator switching

Ini adalah modul utama dari desain kami. Ini parameter oleh bilangan bulat $$$N, M$, yang merupakan ukuran unit kontrol dan data, masing-masing.


Input ke modul ini adalah sinyal clock, a $$$N + 3M$-bit seed, dan sinyal yang ditetapkan. Seed hanyalah gabungan dari reset LFSR kontrol, reset data LFSR, dan bilangan bulat $$$i, j$Outputnya adalah satu bit, bit pseudo acak yang dihasilkan oleh generator switching.


Modul ini mencakup dua $$$M \ kali M$matriks $$$\ mathop M \ nolimits_1, \ mathop M \ nolimits_2$. Matriks ini diperbaiki selama implementasi.


Dua contoh modul eksponensial matriks digunakan untuk menghitung matriks input untuk unit data, di mana input mereka adalah matriks transformasi tetap dan bilangan bulat $$$i, j$, diekstrak dari biji.


Modul Generator Pengalih

Kesimpulan dan rekomendasi

Dalam proyek ini, kami telah menyajikan desain generator switching menggunakan Verilog HDL. Desain ini sepenuhnya berfokus pada perangkat keras, dan menghilangkan penggunaan blok prosedural. Pendekatan semacam itu memungkinkan kinerja maksimum dengan biaya elemen logika dan memori. Untuk beberapa aplikasi dengan batasan elemen logika dan memori, mungkin bermanfaat untuk mengorbankan kinerja dan meningkatkan penggunaan blok prosedural untuk mengurangi penggunaan elemen elektronik.


Salah satu kelemahan dari proyek ini adalah bahwa ia bertanggung jawab memilih indeks perpindahan yang baik pada pengguna. Salah satu kemungkinan kemajuan adalah menambahkan komponen perangkat keras untuk memeriksa validitas indeks switching yang digunakan. Ini membutuhkan implementasi perangkat keras dari algoritma yang kompleks seperti menemukan karakteristik polinomial dari matriks yang diberikan dan memeriksanya untuk primitifitas.


Kemajuan yang mungkin adalah menambahkan generator nomor acak benar untuk memeriksa indeks switching acak, dan menghasilkan pasangan yang valid setelah ditemukan. Dapat dibuktikan bahwa proses ini terhenti setelah waktu singkat dengan probabilitas tinggi.

Referensi

1. Katz, Jonathan, et al. Buku pegangan kriptografi terapan. Pers CRC, 1996.
2. Choi, Jun, dkk. "Generator switching: Generator baru yang dikendalikan jam dengan daya tahan terhadap serangan aljabar dan saluran samping." Entropi 17.6 (2015): 3692-3709.
3. Shamir, Adi. "Stream cipher: mati atau hidup?" ASIACRYPT. 2004
4. LFSR untuk yang belum tahu