Modulasi suara

Sedikit teori yang saya tahu tentang suara - suara adalah:
gelombang, osilasi, osilasi teredam, gelombang dapat digambarkan dari sudut pandang fisika, gelombang dapat dijelaskan dari sudut pandang matematika.

Unduh dan uji programnya


Karena kita memodelkan pada komputer, gelombang kita dideskripsikan menggunakan urutan (deret Fourier) byte (angka -128 hingga 127 dan nol), yaitu array byte.

Persamaan getaran paling baik dijelaskan oleh fungsi SIN.

Setuju, itu akan terlalu sederhana jika kita hanya menjalankan fungsi SIN melalui array.

Oleh karena itu, dipandu oleh artikel tentang deskripsi perangkat synthesizer Yamaha, saya menulis algoritma berikut:

1. Menggunakan fungsi SIN, gelombang utama atau pemodelan dibuat, berikut adalah rumus yang mungkin berguna untuk pengembang lain:

for(int k = 0; k < SoundLabVisual.player.data.length;k++){ double sinusoid = amplitude1 * Math.sin(2 * (3.14/1 ) * k * frequency1 + faza); } 

Dimana:
amplitudo1 - amplitudo
frequency1 - frekuensi osilasi
faza - fase awal osilasi

2. Menggunakan fungsi SIN kedua, gelombang utama dibuat, amplitudo yang merupakan nilai dari gelombang pertama:

 //c   double a1 = 0.1f; //c   double c1 = 0.1f; //c   double d1 = 0.1f; sinusoid = a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 )); 

Tangkapan layar program



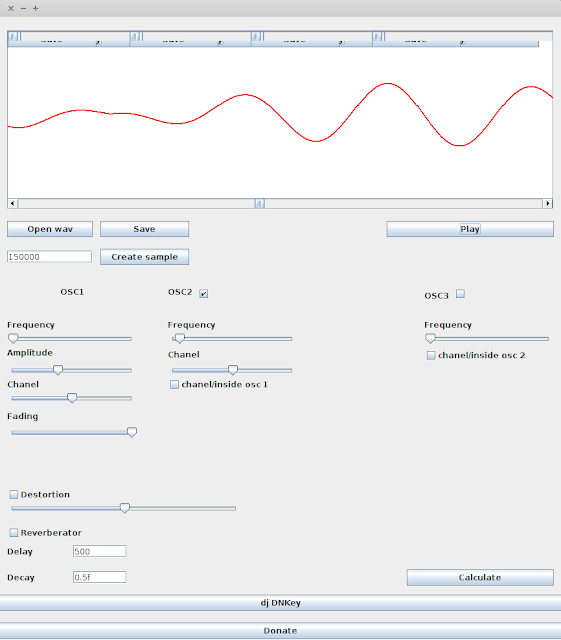
Saya memuat tes suara ke program lmms.



Dengarkan mp3

Algoritme lain akan diterapkan yang akan bekerja pada saluran, jika memungkinkan, saya akan menulis tentang hal itu di artikel kedua.

Perbarui:
Menurut komentar komentator, algoritma sekarang dapat dikalikan sendiri dan di antara mereka sendiri.

 if(jCheckBox8.isSelected()){ sinusoid = (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))) * (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))); }else{ sinusoid = a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 )); } 

Pembaruan 2: Program telah diperbarui, sekarang gelombang dapat dicampur dengan suara.