Artikel ini ditulis tentang analisis dan studi bahan kompetisi untuk mencari kapal di laut.

Mari kita coba memahami bagaimana dan apa yang dicari jaringan dan apa yang ditemukannya. Artikel ini hanyalah hasil dari rasa ingin tahu dan ketertarikan kosong, tidak ada yang ditemukan dalam praktek dan untuk tugas-tugas praktis tidak ada apa-apa untuk copy-paste. Namun hasilnya tidak sepenuhnya diharapkan. Internet penuh dengan deskripsi operasi jaringan di mana penulis menggambarkan dengan indah dan dengan gambar bagaimana jaringan menentukan primitif - sudut, lingkaran, kumis, ekor, dll., Kemudian mereka mencari segmentasi / klasifikasi. Banyak kompetisi dimenangkan menggunakan bobot dari jaringan besar dan lebar lainnya. Sangat menarik untuk memahami dan melihat bagaimana dan primitif apa jaringan membangun.
Kami akan melakukan studi kecil dan mempertimbangkan opsi - alasan dan kode penulis disajikan, Anda dapat memeriksa / menambah / mengubah semuanya sendiri.
Kompetisi pencarian laut yang menakjubkan baru-baru ini berakhir. Airbus mengusulkan menganalisis citra satelit laut dengan dan tanpa kapal. Total 192555 gambar 768x768x3 - itu adalah 340 720 680 960 byte jika uint8 dan empat kali lebih banyak jika float32 (omong-omong float32 lebih cepat daripada float64, akses memori lebih sedikit) dan pada 15606 gambar Anda perlu menemukan kapal. Seperti biasa, semua tempat penting diambil oleh orang-orang yang terlibat dalam ODS (ods.ai), yang alami dan diharapkan, dan saya berharap bahwa kita akan segera dapat mempelajari kereta pikiran dan kode pemenang dan pemenang hadiah.
Kami akan mempertimbangkan masalah serupa, tetapi menyederhanakannya secara signifikan - ambil laut np.random.sample () * 0,5, kita tidak perlu ombak, angin, pantai dan pola serta wajah tersembunyi lainnya. Mari kita buat gambar laut benar-benar acak dalam kisaran RGB dari 0,0 hingga 0,5. Kami akan mewarnai kapal dengan warna yang sama dan untuk membedakannya dari laut, kami akan menempatkannya dalam kisaran 0,5-1,0, dan mereka semua akan memiliki bentuk yang sama - elips dengan ukuran dan orientasi yang berbeda.

Ambil versi jaringan yang sangat umum (Anda dapat mengambil jaringan favorit Anda) dan kami akan melakukan semua percobaan dengannya.
Selanjutnya, kami akan mengubah parameter gambar, membuat interferensi dan membuat hipotesis - jadi kami menyoroti fitur utama yang digunakan jaringan untuk menemukan elips. Mungkin pembaca akan menarik kesimpulannya dan menyangkal penulisnya.
Kami memuat perpustakaan, kami menentukan ukuran array gambarimport numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm_notebook, tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau from keras.models import load_model from keras.optimizers import Adam from keras.layers import Input, Conv2D, Conv2DTranspose, MaxPooling2D, concatenate, Dropout from keras.losses import binary_crossentropy import tensorflow as tf import keras as keras from keras import backend as K from tqdm import tqdm_notebook w_size = 256 train_num = 8192 train_x = np.zeros((train_num, w_size, w_size,3), dtype='float32') train_y = np.zeros((train_num, w_size, w_size,1), dtype='float32') img_l = np.random.sample((w_size, w_size, 3))*0.5 img_h = np.random.sample((w_size, w_size, 3))*0.5 + 0.5 radius_min = 10 radius_max = 30
menentukan fungsi kerugian dan akurasi def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
Kami menggunakan metrik klasik dalam segmentasi gambar, ada banyak artikel, kode dengan komentar dan teks tentang metrik yang dipilih, pada kaggle yang sama ada banyak pilihan dengan komentar dan penjelasan. Kami akan memprediksi topeng piksel - ini adalah "laut" atau "perahu" dan mengevaluasi kebenaran atau kepalsuan prediksi. Yaitu Keempat opsi berikut dimungkinkan - kami memperkirakan dengan benar bahwa suatu piksel adalah "laut", dengan benar memperkirakan bahwa suatu piksel adalah "kapal" atau membuat kesalahan dalam memprediksi "laut" atau "kapal". Jadi, untuk semua gambar dan semua piksel, kami memperkirakan jumlah keempat opsi dan menghitung hasilnya - ini akan menjadi hasil dari jaringan. Dan semakin sedikit prediksi yang salah dan semakin benar, semakin akurat hasilnya dan semakin baik jaringannya.
Dan untuk penelitian, mari kita ambil u-net yang dipelajari dengan baik, yang merupakan jaringan yang sangat baik untuk segmentasi gambar. Jaringan ini sangat umum dalam kompetisi semacam itu dan ada banyak deskripsi, kehalusan aplikasi, dll. Varian dari U-net klasik dipilih dan, tentu saja, dimungkinkan untuk meningkatkannya, menambahkan blok residu, dll. Tetapi “Anda tidak bisa merangkul besarnya” dan melakukan semua percobaan dan tes sekaligus. U-net melakukan operasi yang sangat sederhana dengan gambar - ini mengurangi ukuran gambar dengan beberapa transformasi langkah demi langkah dan kemudian mencoba untuk memulihkan topeng dari gambar yang dikompresi. Yaitu dimensi gambar dalam case kami dibawa ke 32x32 dan kemudian kami mencoba mengembalikan mask menggunakan data dari semua kompresi sebelumnya.
Dalam gambar, skema U-net berasal dari artikel asli, tapi kami redid sedikit, tetapi esensinya tetap sama - kami mengompres gambar → berekspansi menjadi topeng.
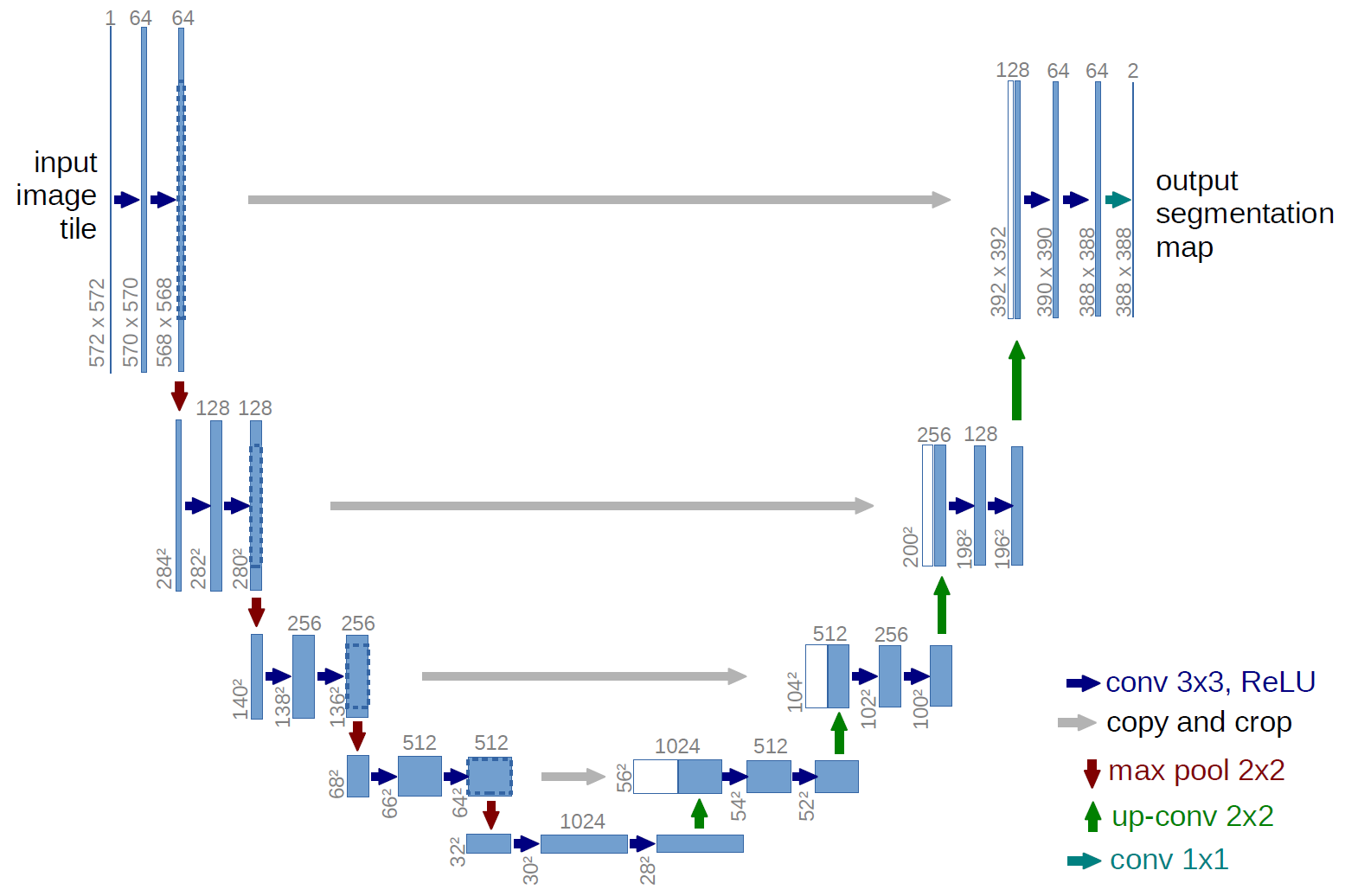
Hanya U-net def build_model(input_layer, start_neurons): conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(input_layer) conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(conv1) pool1 = MaxPooling2D((2, 2))(conv1) pool1 = Dropout(0.25)(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(conv2) pool2 = MaxPooling2D((2, 2))(conv2) pool2 = Dropout(0.5)(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(conv3) pool3 = MaxPooling2D((2, 2))(conv3) pool3 = Dropout(0.5)(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(conv4) pool4 = MaxPooling2D((2, 2))(conv4) pool4 = Dropout(0.5)(pool4)
Percobaan pertama. Termudah
Versi pertama percobaan kami dipilih karena kesederhanaannya menjadi sangat sederhana - laut lebih ringan, kapal lebih gelap. Semuanya sangat sederhana dan jelas, kami berhipotesis bahwa jaringan akan menemukan kapal / elips tanpa masalah dan dengan akurasi apa pun. Fungsi next_pair menghasilkan sepasang gambar / topeng, di mana tempat, ukuran, sudut rotasi dipilih secara acak. Selanjutnya, semua perubahan akan dilakukan pada fungsi ini - perubahan dalam pewarnaan, bentuk, gangguan, dll. Tapi sekarang pilihan termudah, kami menguji hipotesis perahu gelap dengan latar belakang yang terang.
def next_pair(): p = np.random.sample() - 0.5
Kami menghasilkan seluruh kereta dan melihat apa yang terjadi. Itu tampak seperti perahu di laut dan tidak lebih. Semuanya terlihat jelas, jelas dan dapat dimengerti. Lokasi acak dan hanya ada satu elips di setiap gambar.
for k in range(train_num):
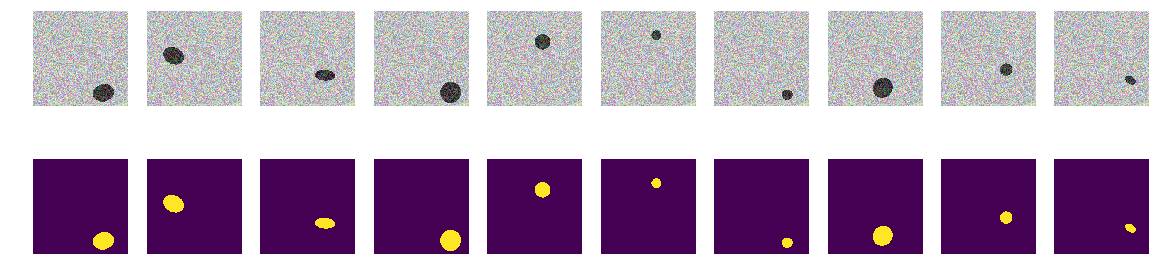
Tidak ada keraguan bahwa jaringan akan belajar dengan sukses dan menemukan elips. Tetapi mari kita uji hipotesis kami bahwa jaringan dilatih untuk menemukan elips / kapal dan pada saat yang sama dengan akurasi tinggi.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.save_weights('./keras.weights') while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.2272 - my_iou_metric: 0.7325 - val_loss: 0.0063 - val_my_iou_metric: 1.0000
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0090 - my_iou_metric: 1.0000 - val_loss: 0.0045 - val_my_iou_metric: 1.0000
Jaringan berhasil menemukan elips. Tetapi sama sekali tidak terbukti bahwa ia mencari elips dalam pemahaman manusia, karena wilayah yang dibatasi oleh persamaan elips dan diisi dengan konten yang berbeda dari latar belakang, tidak ada kepastian bahwa ada bobot jaringan yang mirip dengan koefisien persamaan elips kuadrat. Dan jelas bahwa kecerahan elips kurang dari kecerahan latar belakang dan tidak ada rahasia atau teka-teki - kita menganggap bahwa kita baru saja memeriksa kodenya. Mari kita perbaiki wajah yang jelas, buat latar belakang dan warna elips secara acak juga.
Opsi kedua
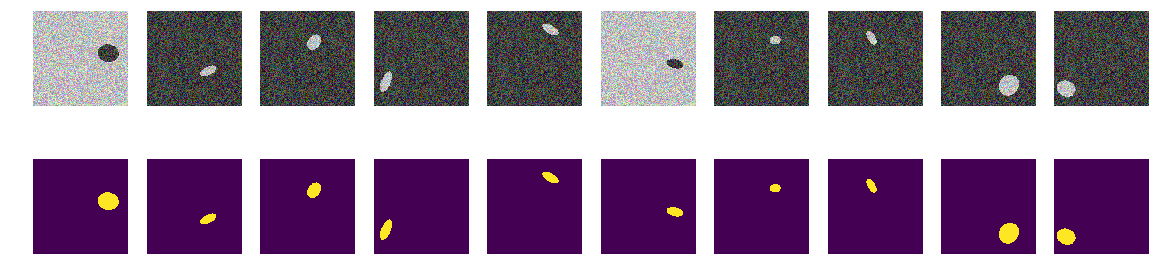
Sekarang elips yang sama di laut yang sama, tetapi warna laut dan, karenanya, perahu dipilih secara acak. Jika laut lebih gelap, kapal akan lebih ringan dan sebaliknya. Yaitu oleh kecerahan kelompok poin tidak mungkin untuk menentukan apakah mereka berada di luar elips, yaitu laut atau ini adalah poin di dalam elips. Sekali lagi, kami menguji hipotesis kami bahwa jaringan akan menemukan elips terlepas dari warnanya.
def next_pair(): p = np.random.sample() - 0.5
Sekarang, dengan pixel dan sekitarnya, tidak mungkin untuk menentukan latar belakang atau elips. Kami juga menghasilkan gambar dan topeng dan melihat 10 pertama di layar.
masker bangunan for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.4652 - my_iou_metric: 0.5071 - val_loss: 0.0439 - val_my_iou_metric: 0.9005
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.1418 - my_iou_metric: 0.8378 - val_loss: 0.0377 - val_my_iou_metric: 0.9206Jaringan dengan mudah mengatasi dan menemukan semua elips. Tapi di sini, ada kekurangan dalam implementasi, dan semuanya jelas - yang lebih kecil dari dua area dalam gambar adalah elips, latar belakang lain. Mungkin ini adalah hipotesis salah, tetapi masih memperbaikinya, tambahkan poligon lain ke gambar dengan warna yang sama dengan elips.
Opsi ketiga
Dalam setiap gambar, kami secara acak memilih warna laut dari dua opsi dan menambahkan elips dan persegi panjang, yang keduanya berbeda dari warna laut. Ternyata "laut" yang sama, juga "perahu" yang dicat, tetapi dalam gambar yang sama kita menambahkan persegi panjang dengan warna yang sama dengan "perahu" dan juga dengan ukuran yang dipilih secara acak. Sekarang asumsi kami lebih rumit, dalam gambar ada dua objek berwarna identik, tetapi kami berhipotesis bahwa jaringan masih akan belajar untuk memilih objek yang tepat.
program untuk menggambar elips dan persegi panjang Seperti sebelumnya, kami menghitung gambar dan topeng dan melihat 10 pasangan pertama.
gambar topeng bangunan elips dan persegi panjang for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 57s 8ms/step - loss: 0.7557 - my_iou_metric: 0.0937 - val_loss: 0.2510 - val_my_iou_metric: 0.4580
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.0719 - my_iou_metric: 0.8507 - val_loss: 0.0183 - val_my_iou_metric: 0.9812Persegi panjang jaringan tidak dapat dikacaukan dan hipotesis kami dikonfirmasi. Dilihat oleh contoh dan diskusi, semua orang di kompetisi Airbus memiliki satu kapal, dan beberapa kapal di dekatnya cukup akurat. Elips dari persegi panjang - yaitu kapal itu dari rumah di pantai, jaringannya dibedakan, meskipun poligonnya sama warnanya dengan elips. Ini bukan masalah warna, karena elips dan persegi panjang sama-sama dicat secara acak.
Opsi keempat
Mungkin jaringan dibedakan oleh segi empat - benar, ubah mereka. Yaitu jaringan dengan mudah menemukan kedua area tertutup terlepas dari bentuk dan membuang salah satu yang merupakan persegi panjang. Ini adalah hipotesis penulis - kami akan memeriksanya, yang akan kami tambahkan bukan persegi panjang, tetapi poligon segi empat yang bentuknya sewenang-wenang. Dan lagi, hipotesis kami adalah bahwa jaringan membedakan elips dari poligon segi empat sewenang-wenang dari pewarnaan yang sama.
Anda tentu saja bisa masuk ke bagian dalam jaringan dan di sana melihat lapisan dan menganalisis makna bobot dan pergeseran. Penulis tertarik pada perilaku jaringan yang dihasilkan, penilaian akan didasarkan pada hasil pekerjaan, meskipun selalu menarik untuk melihat ke dalam.
membuat perubahan pada pembuatan gambar def next_pair(): p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p0 = np.rint(np.random.sample()*(radius_max-radius_min) + radius_min) p1 = np.rint(np.random.sample()*(w_size-radius_max)) p2 = np.rint(np.random.sample()*(w_size-radius_max)) p3 = np.rint(np.random.sample()*2.*radius_min - radius_min) p4 = np.rint(np.random.sample()*2.*radius_min - radius_min) p5 = np.rint(np.random.sample()*2.*radius_min - radius_min) p6 = np.rint(np.random.sample()*2.*radius_min - radius_min) p7 = np.rint(np.random.sample()*2.*radius_min - radius_min) p8 = np.rint(np.random.sample()*2.*radius_min - radius_min) poly = np.array(( (p1, p2), (p1+p3, p2+p4+p0), (p1+p5+p0, p2+p6+p0), (p1+p7+p0, p2+p8), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc = list(set(rr) & set(rr_p)) if len(in_sc) > 0: if np.mean(rr_p) > np.mean(in_sc): poly += np.max(in_sc) - np.min(in_sc) else: poly -= np.max(in_sc) - np.min(in_sc) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img = img_l.copy() img[rr, cc] = img_h[rr, cc] img[rr_p, cc_p] = img_h[rr_p, cc_p] else: img = img_h.copy() img[rr, cc] = img_l[rr, cc] img[rr_p, cc_p] = img_l[rr_p, cc_p] msk = np.zeros((w_size, w_size, 1), dtype='float32') msk[rr, cc] = 1. return img, msk
Kami menghitung gambar dan topeng dan melihat 10 pasangan pertama.
kami membuat gambar topeng elips dan poligon for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

Kami meluncurkan jaringan kami. Biarkan saya mengingatkan Anda bahwa itu sama untuk semua opsi.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.6815 - my_iou_metric: 0.2168 - val_loss: 0.2078 - val_my_iou_metric: 0.4983
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.1470 - my_iou_metric: 0.6396 - val_loss: 0.1046 - val_my_iou_metric: 0.7784
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0642 - my_iou_metric: 0.8586 - val_loss: 0.0403 - val_my_iou_metric: 0.9354
Hipotesis dikonfirmasi, poligon dan elips mudah dibedakan. Pembaca yang penuh perhatian akan mencatat di sini - tentu saja mereka berbeda, pertanyaan omong kosong, AI normal apa pun dapat membedakan kurva urutan kedua dari baris yang pertama. Yaitu jaringan dengan mudah menentukan keberadaan batas dalam bentuk kurva orde kedua. Kami tidak akan berdebat, ganti oval dengan heptagon dan periksa.
Eksperimen kelima, yang paling sulit
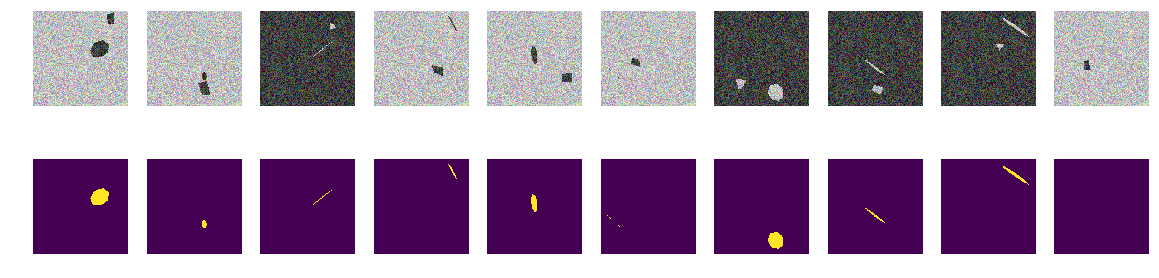
Tidak ada kurva, hanya wajah halus heptagon yang cenderung dan berputar dan poligon segi empat yang sewenang-wenang. Kami memperkenalkan fungsi generator gambar / perubahan topeng - hanya proyeksi heptagon reguler dan poligon segi empat sewenang-wenang dengan warna yang sama.
revisi akhir dari fungsi pembuatan gambar def next_pair(_n = 7): p = np.random.sample() - 0.5 c_x = np.random.sample()*(w_size-2*radius_max) + radius_max c_y = np.random.sample()*(w_size-2*radius_max) + radius_max radius = np.random.sample()*(radius_max-radius_min) + radius_min d = np.random.sample()*0.5 + 1 a_deg = np.random.sample()*360 a_rad = np.deg2rad(a_deg) poly = []
Seperti sebelumnya, kami membuat array dan melihat 10 yang pertama.
masker bangunan for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 54s 7ms/step - loss: 0.5005 - my_iou_metric: 0.1296 - val_loss: 0.1692 - val_my_iou_metric: 0.3722
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.1287 - my_iou_metric: 0.4522 - val_loss: 0.0449 - val_my_iou_metric: 0.6833
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0759 - my_iou_metric: 0.5985 - val_loss: 0.0397 - val_my_iou_metric: 0.7215
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0455 - my_iou_metric: 0.6936 - val_loss: 0.0297 - val_my_iou_metric: 0.7304
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0432 - my_iou_metric: 0.7053 - val_loss: 0.0215 - val_my_iou_metric: 0.7846
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0327 - my_iou_metric: 0.7417 - val_loss: 0.0171 - val_my_iou_metric: 0.7970
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0265 - my_iou_metric: 0.7679 - val_loss: 0.0138 - val_my_iou_metric: 0.8280Ringkasan
Seperti yang Anda lihat, jaringan membedakan antara proyeksi heptagon reguler dan poligon segi empat sewenang-wenang dengan akurasi 0,828 pada set tes. Pelatihan jaringan dihentikan dengan nilai sewenang-wenang 0,75 dan kemungkinan besar akurasinya akan jauh lebih baik. Jika kita melanjutkan dari tesis bahwa jaringan menemukan primitif dan kombinasinya menentukan objek, maka dalam kasus kami ada dua area dengan rata-rata berbeda dari latar belakang, tidak ada primitif dalam pemahaman manusia. Tidak ada garis yang jelas, satu warna, dan tidak ada sudut, masing-masing, hanya area dengan batas yang sangat mirip. Bahkan jika Anda membangun garis, maka kedua objek dalam gambar dibangun dari primitif yang sama.
Sebuah pertanyaan untuk para pecinta - apa yang dianggap jaringan sebagai tanda yang membedakan “kapal” dari “gangguan”? Jelas, ini bukan warna atau bentuk perbatasan kapal. Tentu saja, kita dapat terus mempelajari lebih lanjut konstruksi abstrak dari "laut" / "kapal" ini, kita bukan Akademi Ilmu Pengetahuan dan dapat melakukan penelitian secara eksklusif karena penasaran. Kita dapat mengubah heptagon menjadi oktagon atau mengisi gambar dengan sudut lima dan enam reguler dan melihat apakah jaringan mereka berbeda atau tidak. Saya menyerahkan ini kepada pembaca - walaupun saya juga bertanya-tanya apakah jaringan dapat menghitung jumlah sudut poligon dan, untuk pengujian, mengatur bukan poligon biasa dalam gambar, tetapi proyeksi acak mereka.
Ada sifat-sifat lain yang tak kalah menarik dari perahu semacam itu, dan eksperimen semacam itu berguna karena kita sendiri yang menetapkan semua karakteristik probabilistik dari perangkat yang dipelajari dan perilaku tak terduga dari jaringan yang dipelajari dengan baik akan menambah pengetahuan dan membawa manfaat.
Latar belakang dipilih secara acak, warna dipilih secara acak, lokasi perahu / elips dipilih secara acak. Tidak ada garis dalam gambar, ada area dengan karakteristik berbeda, tetapi tidak ada garis monokrom! Dalam hal ini, tentu saja, ada penyederhanaan dan tugas dapat menjadi lebih rumit - misalnya, pilih warna seperti 0,0 ... 0,9 dan 0,1 ... 1,0 - tetapi untuk jaringan tidak ada perbedaan. Jaringan dapat dan menemukan pola yang berbeda dari yang dilihat dan ditemukan seseorang dengan jelas.
Jika salah satu pembaca tertarik, maka Anda dapat terus meneliti dan memilih di jaringan, jika apa yang tidak berhasil atau tidak jelas, atau jika pemikiran baru dan bagus muncul dan mengesankan dengan keindahannya, maka Anda selalu dapat berbagi dengan kami atau bertanya kepada master (dan juga grandmaster) dan meminta bantuan yang memenuhi syarat dalam komunitas ODS.