Bukti baru, yang ditulis oleh penulis fiksi ilmiah Australia Greg Egan, dan bukti 2011, diposting secara anonim secara online, telah diakui sebagai terobosan signifikan dalam studi misteri yang telah diteliti oleh para ahli matematika selama 25 tahun.

Pada 16 September 2011, seorang penggemar anime memposting pertanyaan matematika 4chan pada seri kultus "The
Melancholy of Haruhi Suzumiya " di forum. Musim pertama pertunjukan, di mana ada perjalanan waktu, ditunjukkan dalam urutan yang berbeda dari yang kronologis, dan selama pertunjukan berikutnya dan dirilis pada DVD urutan episode sekali lagi diubah. Di Internet, penggemar berargumen dalam urutan apa lebih baik untuk menonton serial tersebut, dan penulis pertanyaan bertanya: jika audiens ingin melihat seri dalam semua pesanan yang mungkin, berapa banyak episode yang akan ada dalam daftar terpendek mereka? [
mengacu pada daftar di mana Anda dapat menemukan urutan episode / perkiraan. perev. ]
Dalam waktu kurang dari satu jam, satu penulis anonim memberikan
jawaban untuk pertanyaan - bukan solusi lengkap, tetapi batas bawah pada jumlah episode yang diperlukan. Dari alasannya, berlaku untuk sejumlah episode, disimpulkan bahwa untuk musim pertama Haruhi, yang terdiri dari 14 episode, pemirsa harus menonton setidaknya 93.884.313.611 episode berturut-turut untuk mempelajari semua kemungkinan permutasi. "Periksa bukti adanya kekurangan yang mungkin saya lewatkan," tulis penulis tanggapan.
Selama tujuh tahun buktinya tidak diketahui dalam komunitas matematika - ternyata pada saat itu hanya satu ahli matematika profesional yang memperhatikannya, dan ia tidak mempelajarinya dengan cukup teliti. Namun, tiba-tiba bulan lalu, penulis fiksi ilmiah Australia
Greg Egan membuktikan
batas atas baru pada jumlah episode yang dibutuhkan. Penemuan Egan membangkitkan kembali minat dalam tugas dan menarik perhatian pada catatan mengenai batas bawah tahun 2011. Kedua bukti ini sekarang dianggap sebagai terobosan signifikan dalam studi misteri yang telah diteliti oleh matematikawan selama setidaknya 25 tahun.
Matematikawan dengan cepat memeriksa batas atas dari Egan, yang, seperti batas bawah, berlaku untuk urutan berapa pun panjangnya. Kemudian Robin Houston, seorang matematikawan di Kiln, sebuah perusahaan visualisasi data, dan
Jay Panton dari Marquette University di Milwaukee secara independen mengkonfirmasi karya seorang penulis anonim dengan 4chan. "Banyak upaya dilakukan untuk memverifikasi validitas hipotesis ini," kata Panton, karena ide-ide kunci dari bukti tersebut tidak diungkapkan dengan cukup jelas.
Dan sekarang, Houston dan Panton, bersama dengan
Vince Vater dari University of Florida, telah menulis sebuah
karya formal . Di dalamnya, mereka menunjukkan penulis pertama sebagai "poster 4chan anonim".
"Yang aneh adalah bahwa bukti yang sangat elegan dari fakta yang sebelumnya tidak diketahui ini muncul di tempat yang tidak mungkin," kata Houston.
Kota permutasi
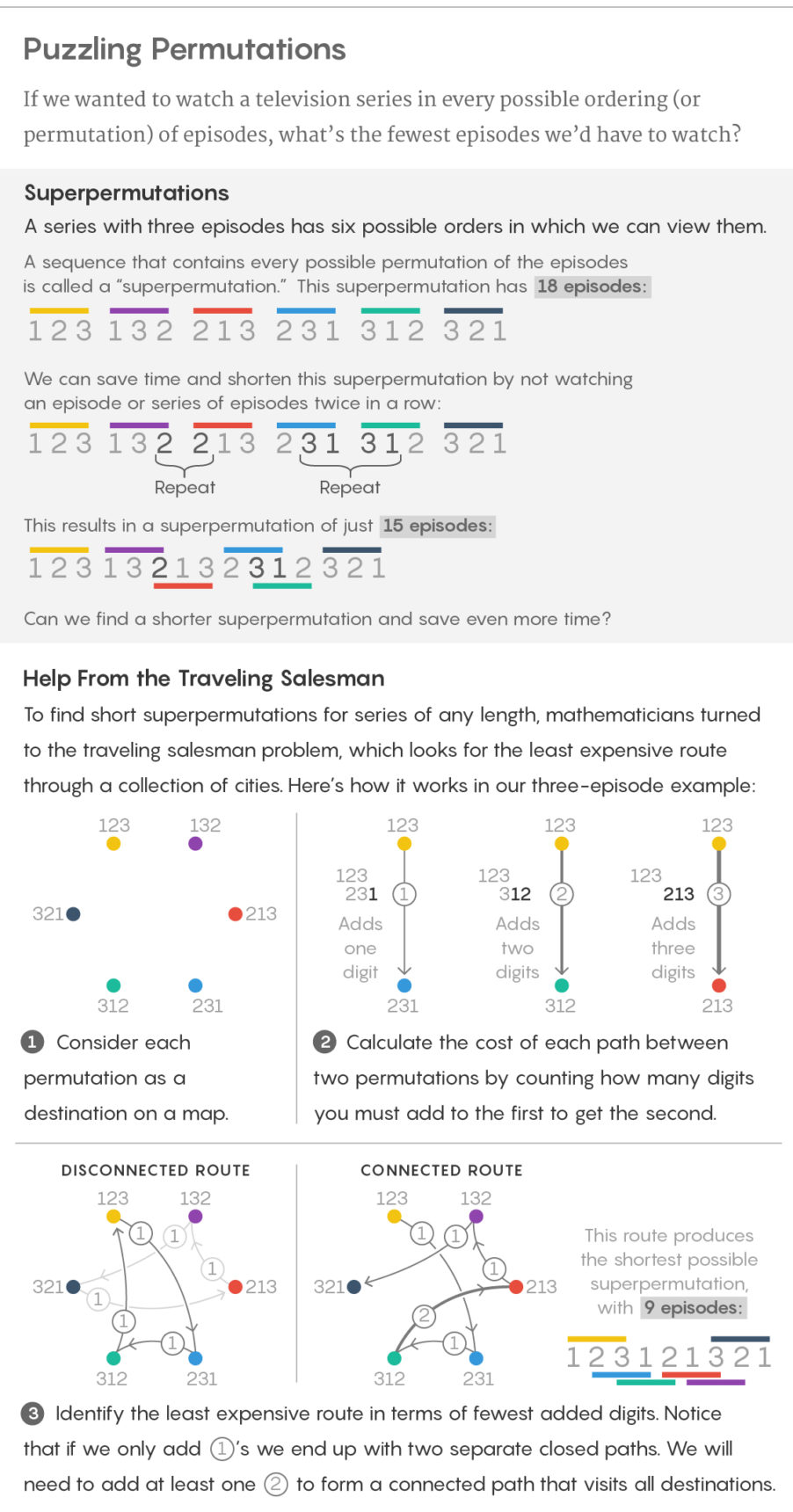
Jika seri ini hanya memiliki tiga episode, ada enam cara yang mungkin untuk menontonnya: 123, 132, 213, 231, 312 dan 321. Mereka dapat dilem bersama dan membuat daftar 18 episode, termasuk setiap versi dari urutan. Namun, ada juga metode perekatan yang lebih efisien: 123121321. Urutan seperti itu yang mengandung semua permutasi dari set n karakter disebut super permutasi.
Pada tahun 1993, Daniel Ashlock dan Janet Tilotson menemukan bahwa ketika mempelajari permutasi super terpendek untuk berbagai nilai n, faktorial dengan cepat mulai muncul - nilai-nilai yang sama ditulis dalam bentuk n!, Mis., Mengalikan semua angka dari 1 ke n (misalnya, 4 ! = 4 * 3 * 2 * 1).
Jika hanya ada 1 episode dalam seri Anda, maka panjang permutasi super terpendek adalah 1! (Juga dikenal sebagai unit tua yang baik). Untuk serangkaian dua episode, permutasi super terpendek (121) memiliki panjang 2! +1! .. Untuk tiga episode (contoh di atas), panjangnya adalah 3! + 2! +1!, Dan untuk empat episode (123412314231243121342132413214321) itu akan menjadi 4! + 3! + 2! +1! .. Aturan faktorial diterima secara umum (walaupun tidak ada yang bisa membuktikan bahwa itu benar untuk semua n), dan kemudian matematikawan mengonfirmasi untuk n = 5.
Kemudian pada tahun 2014, Houston mengesankan ahli matematika,
menunjukkan bahwa untuk n = 6 aturan berhenti bekerja. Aturan memperkirakan bahwa akan diperlukan 873 episode untuk menonton enam episode dalam setiap cara yang mungkin, tetapi Houston menemukan cara untuk melakukannya di 872. Dan karena ada cara sederhana untuk mengubah permutasi super pendek untuk n karakter menjadi permutasi super pendek untuk n + 1 karakter, contoh Houston berarti aturan tersebut faktorial tidak bekerja untuk semua n> 6.
Membangun Houston mengubah tugas permutasi super menjadi masalah salesman keliling terkenal, yang mencari jalan terpendek melalui beberapa kota. Secara khusus, permutasi-super dikaitkan dengan masalah salesman “asimetris”, di mana setiap jalur antara dua kota memiliki harganya sendiri (tidak harus sama di kedua arah), dan tujuannya adalah untuk menemukan cara termurah melalui semua kota.
Transformasi ini mudah dimengerti: bayangkan bahwa setiap permutasi adalah kota, dan bayangkan jalur dari setiap permutasi ke setiap permutasi lainnya. Dalam masalah permutasi super, kita membutuhkan urutan digit terpendek di mana semua permutasi hadir, jadi tujuan kami adalah untuk melewati semua permutasi untuk menambahkan nomor sesedikit mungkin ke permutasi awal. Kami mengumumkan bahwa biaya setiap jalur hanyalah jumlah digit yang perlu kami lampirkan pada akhir permutasi pertama untuk mendapatkan yang kedua. Dalam contoh dengan n = 3, jalur dari 231 ke 312 biaya $ 1, karena kita hanya perlu menambahkan 2 ke akhir 231 untuk mendapatkan 312, dan jalur dari 231 ke 132 biaya $ 2, karena kita perlu menambahkan 32. Dalam formulasi ini, cara termurah melalui semua kota secara langsung berhubungan dengan permutasi super terpendek.
Transformasi seperti itu berarti bahwa Houston dapat mengarahkan semua kemampuan algoritma untuk memecahkan masalah salesman keliling ke masalah super permutasi. Masalah ini dikenal karena milik kelas NP-kompleks, yang berarti tidak adanya algoritma yang efektif yang dapat menyelesaikannya dalam kasus umum. Namun, ada algoritma yang secara efektif dapat memecahkan beberapa jenis masalah, dan algoritma lainnya dapat menghasilkan solusi perkiraan yang baik. Houston menggunakan salah satu dari yang terakhir untuk mengeluarkan permutasi super panjang 872 digit.
Karena dia hanya memberikan solusi perkiraan, itu mungkin bahkan bukan permutasi super yang paling ideal. Matematikawan sekarang melakukan pencarian komputasi yang banyak untuk permutasi 6 karakter terpendek, kata Panton. "Kami tahu bahwa pencarian kami akan berakhir dalam waktu yang terbatas, tetapi kami tidak tahu apakah itu akan memakan waktu seminggu atau sejuta tahun," katanya. "Tidak ada bilah kemajuan."
Pesanan salah
Pada saat karya Houston muncul, sebuah pos anonim tentang 4chan telah ada di sudut internetnya selama hampir tiga tahun. Seorang ahli matematika,
Nathaniel Johnston dari Mount Ellison University, melihat salinan dari posting ini di situs lain beberapa hari setelah posting ini muncul - dan bukan karena dia seorang pecinta anime, tetapi karena dia memasukkan berbagai permintaan ke Google, terkait dengan permutasi super.
Johnston membaca buktinya dan itu tampaknya dapat diandalkan untuknya, tetapi dia tidak menghabiskan energinya untuk pemeriksaan menyeluruh. Pada saat itu, matematikawan percaya bahwa rumus faktorial untuk permutasi-super kemungkinan besar benar, dan ketika Anda berpikir bahwa Anda tahu jawaban pasti untuk pertanyaan tersebut, Anda tidak tertarik pada batas bawah estimasi. Dengan kata lain, episode seri tentang permutasi super berjalan dengan urutan yang salah.
Setelah itu, Johnston menyebutkan batas bawah pada
sepasang situs web , tetapi "Saya tidak berpikir ada orang yang menaruh perhatian khusus pada ini," katanya.
Kemudian, pada tanggal 26 September 2018, ahli matematika
John Baez dari University of California di Riverside mentweet sebuah
posting tentang penemuan Houston tahun 2014, sebagai bagian dari serangkaian tweet tentang pola matematika yang jelas yang berhenti bekerja.
Catatan perev.: tidak ada serangkaian tweet yang besar, hanya tiga. Dua lainnya juga menarik dalam diri mereka sendiri, meskipun mereka tidak terkait dengan artikel ini. Satu mengatakan bahwa 6 adalah jarak paling populer antara dua bilangan prima yang berdekatan untuk semua bilangan prima yang lebih kecil dari 17.427.000.000.000.000.000.000.000.000.000.000.000.000, Dan kemudian pola ini tiba-tiba berhenti bekerja! Yang kedua menunjukkan koneksi integral, fungsi trigonometrik, dan angka following berikut ini

Tetapi hanya untuk n <9,8 × 10 42 !Tweet-nya menarik perhatian Egan, yang belajar matematika beberapa dekade yang lalu, sebelum karirnya sebagai penulis fiksi ilmiah yang diakui dimulai (kisah sukses pertamanya, secara kebetulan, disebut "Kota Permutasi"). "Saya tidak pernah berhenti tertarik pada matematika," tulis Egan dalam surat.
Egan bertanya-tanya apakah mungkin untuk membuat permutasi super bahkan lebih pendek dari Houston. Dia terjun ke studi literatur tentang cara membuat cara pintas dalam jaringan permutasi, dan setelah beberapa minggu menemukan apa yang dia butuhkan. Dalam beberapa hari, ia menyimpulkan batas atas baru pada panjang permutasi super terpendek dari n karakter: n! + (n - 1)! + (n - 2)! + (n - 3)! + n - 3. Ini mirip dengan rumus faktorial, dari mana banyak anggota dikeluarkan.
"Ini benar-benar melanggar batas atas sebelumnya," kata Houston.
Batas bawah penulis pos pada 4chan sangat menggoda dengan batas atas baru: n! + (n - 1)! + (n - 2)! + n - 3. Setelah publikasi hasilnya, Egan Johnston mengingatkan ahli matematika tentang bukti penulis anonim, dan Houston dan Panton segera membuktikan kebenarannya. Seperti dalam pekerjaan Houston, batas bawah dan atas yang baru cocok untuk permutasi super dari sudut pandang masalah salesman keliling: batas bawah menunjukkan bahwa jalur melalui semua kota harus melalui beberapa jumlah jalur minimum bernilai lebih dari $ 1, dan batas atas menciptakan jalur khusus untuk masing-masing, hanya menggunakan senyawa bernilai $ 1 dan $ 2.
Sekarang, para peneliti sedang mencoba untuk menyatukan batas atas dan bawah, dan menemukan formula tunggal yang memecahkan masalah super permutasi. "Mungkin, pada akhirnya, orang masih akan memecahkan teka-teki ini," prediksi Baez. "Sekarang semuanya terlihat bagus."
Untuk penggemar Haruhi, solusi Egan memberikan instruksi yang tepat tentang cara melihat semua opsi yang mungkin untuk musim pertama, menggunakan total 93.924.230.411. Anda dapat mulai menonton hari ini, atau Anda dapat menunggu sampai matematikawan bahkan dapat memotong nomor ini. Batas bawah dari penulis anonim membuktikan bahwa pengurangan ini tidak akan menyelamatkan mereka lebih dari 40 juta episode - namun, ini sudah cukup untuk mulai mempersiapkan musim kedua.