Accelerometer dan Giroskop MEMS - Memahami Spesifikasi

"Houston, kami memiliki masalah," terdengar suara lelah di otak saya, mencoba untuk melewati InvenSense Datasheet IMU MPU-9250 di malam hari. Ketika semua kata-kata secara individu dapat dimengerti, tetapi hubungan mereka bingung untuk tidak mungkin. Semuanya dimulai dengan parameter LSB, yang hanya samar-samar saya ingat bahwa dalam terjemahan itu Least Significant Bit. Lalu pergi "Resolusi", "Sensitivitas", dan lebih jauh saya menyadari bahwa teks yang dihasilkan sudah bisa berjudul "Lembar Data untuk Dummies".

Sedikit tentang blok utama dari modul inersia.

MEMS giroskop

MPU-9250 terdiri dari tiga sensor kecepatan sudut vibrasi uniaksial independen (MEMS giroskop) yang merespons rotasi di sekitar sumbu X-, Y-, Z. Dua massa yang ditangguhkan berosilasi dalam sumbu yang berlawanan. Dengan munculnya kecepatan sudut, efek Coriolis menyebabkan perubahan arah getaran ( $$$\ vec {F} _K = -2m [\ vec {\ omega} \ kali \ vec {v} _r]$ yang diperbaiki oleh sensor kapasitif. Komponen kapasitif diferensial yang diukur sebanding dengan sudut gerakan [Waktu Elektronik]. Sinyal yang dihasilkan diperkuat, didemodulasi dan disaring, menghasilkan tegangan yang sebanding dengan kecepatan sudut rotasi. Sinyal ini didigitalkan menggunakan on-board 16-bit ADC. Tingkat sampel dapat bervariasi dari 3,9 hingga 8000 sampel per detik (sampel per detik, SPS), dan filter low-pass yang ditentukan pengguna menyediakan berbagai frekuensi cutoff yang mungkin. Filter low-pass diperlukan, khususnya, untuk menghilangkan getaran dari motor (sebagai aturan, di atas 20-25 Hz).

Three Axis MEMS Accelerometer

Menggunakan massa uji terpisah untuk setiap sumbu, yang bergeser saat akselerasi terjadi di sepanjang sumbu ini (ditetapkan oleh sensor kapasitif). Arsitektur MPU-9250 mengurangi paparan terhadap penyimpangan suhu dan variasi dalam parameter listrik. Ketika perangkat terletak pada permukaan datar, itu akan mengukur 0g sepanjang sumbu X- dan Y dan +1 g di sepanjang sumbu Z. Faktor skala ( faktor skala - rasio perubahan sinyal keluaran terhadap perubahan sinyal keluaran diukur) dikalibrasi di pabrik dan tidak tergantung pada tegangan suplai. Setiap sensor dilengkapi dengan ADC sigma-delta individu (terdiri dari modulator dan filter low-pass digital, lebih banyak tentang perangkat di [Easyelectronics]), output digital yang memiliki rentang pengukuran yang dapat disesuaikan.

Dan hanya tentang magnetometer MEMS tiga sumbu

Berdasarkan teknologi efek Hall presisi tinggi. Ini termasuk sensor magnetik yang menentukan kekuatan medan magnet bumi di sepanjang sumbu, sirkuit kontrol, sirkuit amplifikasi sinyal dan sirkuit komputasi untuk memproses sinyal dari masing-masing sensor. Setiap ADC memiliki resolusi 16 bit, rentang pengukuran $$$\ pm 4800 \ mu T$ . Untuk mengukur medan magnet yang lemah, baik satuan dalam sistem SI microtesley (μT) atau gauss (G, sistem GHS) digunakan: $$$1 G. = 100 \ mu T$ , [Pilot Radio]).

Jadi apa itu LSB dan bagaimana cara menghitungnya? Instruksi produksi

Katakanlah accelerometer kami sekarang beroperasi dalam rentang pengukuran $$$FS = \ pm 2g$ , yaitu, kisaran penuh dari nilai yang mungkin akan $$$2 \ cdot FS = 4g$ . Nilai voltase yang sesuai di-digital oleh 16-bit ADC, yang dapat membagi seluruh interval sebanyak mungkin $$$2 ^ {16} = 65536$ langkah-langkah. Peningkatan minimum yang dapat dideteksi hanya satu langkah $$$LSB = 2 \ cdot FS / 65536$ . Di sini kita harus ingat bahwa akun dilakukan dari awal, sehingga sebenarnya nilai maksimum yang diukur akan menjadi $$$2 \ cdot FS_ {true} = (2 ^ {16} - 1) * LSB = 65535 * LSB = 2 \ cdot FS - LSB$ . Artinya, semakin banyak bit dalam kata digital ADC atau DAC, semakin kecil perbedaannya. Dalam hal ini, sensitivitas (kadang-kadang disebut faktor skala, faktor skala sensitivitas) dari sensor dalam rentang tertentu akan ditentukan sebagai rasio sinyal keluaran listrik dan dampak mekanis. Diindikasikan secara tradisional untuk frekuensi sinyal 100 Hz dan suhu $$$T = + 25 ^ {\ circ} C.$ Untuk MPU-9250, sensitivitasnya adalah $$$2 ^ {16} / (2 \ cdot FS)$ langkah untuk setiap g atau $$$^ {\ circ} / s$ ( $$$LSB / g$ , $$$LSB / (^ {\ circ} / s)$ ), untuk IMU lain, BMI088 dari Bosch Sensortec, sensitivitas gyro dihitung dengan cara yang sama, dan untuk akselerometer digunakan $$$(2 ^ {16} -2 ^ 4) / (2 \ cdot FS)$ langkah-langkah untuk masing-masing g.



Kami mengeluarkan varian FS dari spesifikasi untuk giroskop dan, agar tidak bangun dua kali, akselerometer.





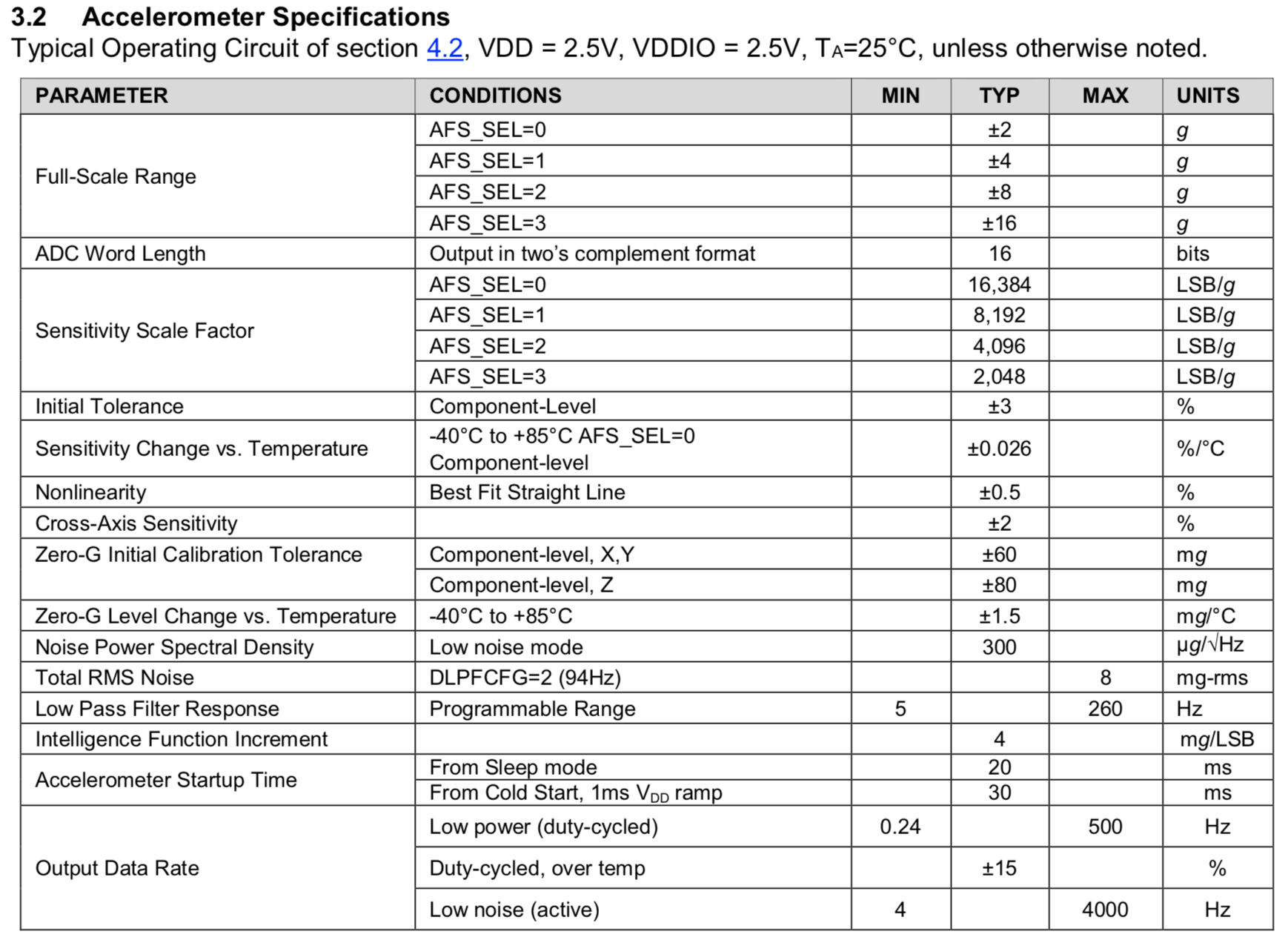
Saya juga mengambil FS untuk akselerometer dari dokumentasi untuk BMI088 (lihat di bawah).

Giroskop, 16 bit $$$(2 ^ N = 65535)$		Akselerometer, 16 bit $$$(2 ^ N = 65535)$
Rentang (FS) $$$^ {\ circ} / s$ (dps)	LSB, $$$^ {\ circ} / s$ (dps)	Range (FS), g	LSB mg
$$$\ pm $ 12$ (FS = 250)	0,004	$$$\ pm $$ (FS = 4)	0,06
$$$\ pm $ 25$ (FS = 500)	0,008	$$$\ pm 3$ (FS = 6)	0,09
$$$\ pm $ 50$ (FS = 1000)	0,0015	$$$\ pm $$ (FS = 8)	0,12
$$$\ pm $ 100$ (FS = 2000)	0,03	$$$\ pm $$ (FS = 12)	0,18
$$$\ pm $ 200$ (FS = 4000)	0,06	$$$\ pm 8$ (FS = 16)	0,24
		$$$\ pm $ 1$ (FS = 24)	0,37
		$$$\ pm 16$ (FS = 32)	0,48
		$$$\ pm 24$ (FS = 48)	0,73

Segalanya, tampaknya, jatuh ke tempatnya, Anda bisa melanjutkan. Dalam beberapa kasus (di bawah ini, misalnya, kliping dari dokumentasi untuk BMI088), parameter seperti resolusi ditunjukkan secara terpisah.

Bahkan, tampaknya itu harus menjadi LSB. Tetapi mengapa kita melihat satu nilai alih-alih beberapa terikat pada rentang tertentu? Saya harus memperluas daftar sumber yang dipelajari untuk mencari jawaban.

Apa itu Resolusi?

Nilai minimum yang dapat dipercaya sensor sangat penting ketika mencoba untuk menyeimbangkan antara harga dan kinerja. Ini bukan akurasi - sensor resolusi tinggi mungkin tidak terlalu akurat, sama seperti sensor resolusi rendah di area tertentu mungkin memiliki akurasi yang cukup. Sayangnya, LSB hanya mendefinisikan nilai pembeda minimum teoretis, asalkan kita dapat menggunakan semua 16 bit ADC. Ini adalah resolusi di dunia digital. Secara analog, beberapa langkah akan berisik dan jumlah bit efektif akan lebih sedikit.

Apa karakteristik kebisingan dan dari mana datangnya?

Sumber kebisingan dapat secara umum dibagi menjadi derau elektronik dari rangkaian yang mengubah gerak menjadi sinyal tegangan (derau termal Johnson, derau tembakan, derau flicker 1 / f merah muda, dll.) Dan mekanis mekanis (Brown karena adanya bagian bergerak kecil) dari sensor itu sendiri. Karakteristik yang terakhir akan tergantung pada frekuensi resonansi dari bagian mekanis sistem $$$f_0$ (Frekuensi osilasi alami dari sensor $$$\ omega_0 = 2 \ pi / f_0$ )

RMS noise pada seluruh rentang spektral - Total RMS (Root mean square) Noise

Tingkat kebisingan dapat ditentukan dengan beberapa cara. Anda dapat mempertimbangkannya dalam domain waktu atau frekuensi (setelah transformasi Fourier). Dalam kasus pertama, noise residual diambil sebagai nilai rms dari sinyal dari sensor tetap (pada kenyataannya, ini adalah standar deviasi untuk pengambilan sampel pada $$$\ overline x = 0$ ) untuk jangka waktu tertentu:

$$

$$x_ {RMS} = \ sigma_X = \ sqrt {\ sum_ {i = 1} ^ n {(x_i - \ overline x)} ^ 2 \ over {n-1}}$$

Akselerasi atau kecepatan rotasi sudut kurang dari tingkat kebisingan broadband tidak dapat dibedakan - ini adalah resolusi aktual. Nilai rms dari tegangan atau arus bolak-balik (sering disebut aktif atau efektif) sama dengan nilai sinyal konstan yang tindakannya akan melakukan pekerjaan yang sama dalam beban aktif (resistif) selama periode tersebut. Pendekatan ini paling efektif ketika mengevaluasi noise broadband, di mana white noise mendominasi.

Untuk white noise, rasio amplitudo (nilai puncak sesaat) ke rms dengan probabilitas 99,9% adalah $$$N_ {PP} / N_ {RMS} = 6.6.$ Rasio ini disebut faktor silang (faktor puncak, rasio silang). Anda dapat memilih probabilitas 95,5% - faktor silang akan menjadi 4.



Faktanya, sinyal noise tidak berperilaku sangat baik dan dapat menghasilkan puncak yang meningkatkan faktor silang hingga 10 kali lipat. Dalam beberapa spesifikasi Anda dapat menemukan nilainya $$$N_ {PP}$ atau pengali itu sendiri.

Dalam pita frekuensi rendah sempit 0,1-10 Hz, peran utama dimainkan oleh derau flicker “1 / f”, yang diperkirakan menggunakan amplitudo sinyal derau puncak-ke-puncak.

Kepadatan spektrum

Kadang-kadang sinyal lebih nyaman untuk dipertimbangkan dalam domain frekuensi, di mana deskripsinya disebut spektrum (ketergantungan amplitudo dan fase pada frekuensi). Salah satu karakteristik kebisingan yang mungkin ada dalam spesifikasi disebut kerapatan spektral daya (PSD), kerapatan spektral noise, kerapatan daya derau, atau hanya kerapatan derau ). Menjelaskan distribusi daya derau pada rentang frekuensi. Terlepas dari representasi sinyal listrik melalui arus atau tegangan, daya sesaat yang dihamburkan pada beban dapat dinormalisasi (R = 1 Ohm) dan dinyatakan sebagai $$$p (t) = {\ nu} ^ 2 (t) / R = i ^ 2 (t) R = x ^ 2 (t).$ Daya rata-rata hilang oleh sinyal selama periode waktu tertentu $$$(- T / 2, T / 2),$

$$

$$P_x ^ T = \ frac {1} {T} \ int ^ {T / 2} _ {- T / 2} x ^ 2 (t) \, dt.$$

Daya adalah tingkat input energi. Sinyal yang ditentukan dan non-periodik ditentukan melalui energi. Sinyal-sinyal periodik dan acak diekspresikan dalam bentuk kekuatan, karena mereka tidak dibatasi dalam waktu dan, karenanya, dalam energi, dan pada waktu tertentu kekuatan rata-rata mereka adalah nol

$$

$$P_x = \ lim_ {T \ to \ infty} \ frac {1} {T} \ int ^ {T / 2} _ {- T / 2} x ^ 2 (t) \, dt.$$

Anda dapat mengingat [Sklyar] bahwa sinyal periodik sewenang-wenang diekspresikan melalui kombinasi harmonik dalam jumlah tak terbatas dengan frekuensi yang meningkat:

$$

$$x (\ lambda) = \ frac {a_0} {2} + \ sum_ {n = 1} ^ {\ infty} (a_n \ cos n \ lambda + b_n \ sin n \ lambda),$$

bahwa setelah mewakili kosinus dan sinus dalam bentuk eksponensial

$$

$$\ cos \ lambda = \ frac {e ^ {i \ lambda} + e ^ {- i \ lambda}} {2}, \ sin \ lambda = \ frac {e ^ {i \ lambda} - e ^ {- i \ lambda}} {2i}$$

dan penggantian $$$\ lambda = \ omega t = 2 \ pi f_0 t = \ frac {2 \ pi t} {T_0}$ dapat ditulis sebagai

$$

$$x (t) = \ frac {a_0} {2} + \ frac {1} {2} \ sum_ {n = 1} ^ {\ infty} [(a_n - ib_n) e ^ {dalam \ omega t} + (a_n + ib_n) e ^ {- dalam \ omega t}] = \ sum_ {n = - \ infty} ^ {\ infty} c_n e ^ {dalam \ omega t},$$

di mana koefisien kompleks (komponen spektral) dari deret Fourier untuk $$$x (t)$ ,

$$$$ menampilkan $$ \ mulai {persamaan} c_n = \ frac {1} {T_0} \ int ^ {T_0 / 2} _ {- T_0 / 2} x (t) e ^ {- di \ omega t}, dt = \ begin {cases} \ frac {1} {2} (a_n-ib_n), & n> 0 \\ \ frac {a_0} {2}, & n = 0 \\ \ frac {1} {2} ( a_n + ib_n), & n <0 \ end {cases} \ end {persamaan} $$ menampilkan $$

Dalam kasus umum, koefisien ini dapat direpresentasikan sebagai berikut:

$$

$$c_n = | c_n | e ^ {i \ theta_n},$$

$$

$$| c_n | = \ frac {1} {2} \ sqrt {a_n ^ 2 + b_n ^ 2}, \ theta_n = \ arctan \ kiri (\ frac {b_n} {a_n} \ kanan), b_0 = 0, c_0 = \ frac {a_0} {2}.$$

Amplitudo dan spektrum fase disebut grafik dependensi. $$$| c_n |$ dan $$$\ theta_n$ dari frekuensi. Kerapatan spektral daya $$$PSD (f)$ sinyal periodik $$$x (t)$ memberikan distribusi daya sinyal pada rentang frekuensi:

$$

$$PSD (f) = \ jumlah ^ {\ infty} _ {n = - \ infty} | c_n | ^ 2 \ delta (f-nf_0)$$

dan memiliki dimensi $$$[W / Hz] = [x ^ 2 / Hz].$ Kekuatan normal rata-rata sinyal aktual akan

$$

$$P_x = \ int ^ {\ infty} _ {- \ infty} PSD (f), df.$$

Sinyal acak non-periodik (khususnya, noise) dapat digambarkan sebagai periodik dalam arti terbatas. Jika $$$T_0$ cenderung tak terhingga, urutan impuls berubah menjadi impuls terpisah $$$x (t)$ , jumlah garis spektral cenderung tak terhingga, grafik spektrum berubah menjadi spektrum frekuensi yang halus $$$X (f).$ Untuk kasus yang membatasi ini, kita dapat menentukan sepasang transformasi Fourier integral

$$

$$X (f) = \ int ^ {\ infty} _ {- \ infty} x (t) e ^ {- i 2 \ pi f t}, dt$$

dan

$$

$$x (t) = \ int ^ {\ infty} _ {- \ infty} X (f) e ^ {i 2 \ pi ft}, df,$$

dimana $$$X (f)$ - Gambar Fourier.

Kepadatan spektral daya dari sinyal acak ditentukan melalui batas

$$

$$PSD (f) = \ lim_ {T \ to \ infty} \ frac {1} {T} | X_T (f) | ^ 2.$$

dan menjelaskan distribusi daya sinyal dalam rentang frekuensi.

Karena kami mengasumsikan bahwa rata-rata untuk white noise dari sensor dalam keadaan stasioner adalah nol ( $$$\ overline x = \ overline x ^ 2 = 0$ ), maka kuadrat dari nilai rms sama dengan varians dan mewakili daya total dalam beban normal:

$$

$$Noise_ {RMS} ^ 2 = \ sigma_x ^ 2 = P_x = \ int ^ {\ infty} _0 PSD (f), df = \ int ^ {Bandwidth} _0 PSD (f), df = PSD (Badnwidth - 0)$$

$$

$$Noise RMS = \ sqrt {Noise Density \ times Bandwidth}$$

Kami melihat dalam spesifikasi - di sana, sebenarnya, akar kuadratnya dengan dimensi yang sesuai ditunjukkan dengan nama kepadatan spektral $$$[^ {\ circ} / s / \ sqrt {Hz}]$ atau $$$[\ mu g / \ sqrt {Hz}].$ Artinya, nilai noise RMS tanpa menunjukkan pita frekuensi yang dibaca (Bandwidth) tidak ada artinya.

Sedikit lagi tentang pilihan bandwidth

Pada output sensor MEMS, kami mendapatkan sinyal dari frekuensi yang berbeda. Diasumsikan bahwa kita memiliki gagasan tertentu tentang proses yang kita ukur sebelumnya. Misalnya, ketika menentukan vektor percepatan drone, derau adalah getaran perangkat. Anda dapat memisahkan mereka dari sinyal yang berguna menggunakan filter low-pass yang memotong semua frekuensi di atas yang ditentukan (misalnya, 200 Hz). MPU-9250 menyediakan kemampuan untuk menyesuaikan frekuensi cutoff dari filter low-pass menggunakan parameter dengan nama ajaib DLPFCFG . Itu adalah singkatan dari Digital Low Pass Filter Configuration. Lebih jauh dalam spesifikasi, ekspresi yang tidak kalah misterius dari tipe (DLPFCFG = 2, 92Hz) muncul di sana-sini, tetapi untuk decoding saya harus naik ke dokumen lain, "Daftar Peta dan Deskripsi". Ini menunjukkan set bit mana register harus ditulis untuk mencapai efek yang diinginkan:



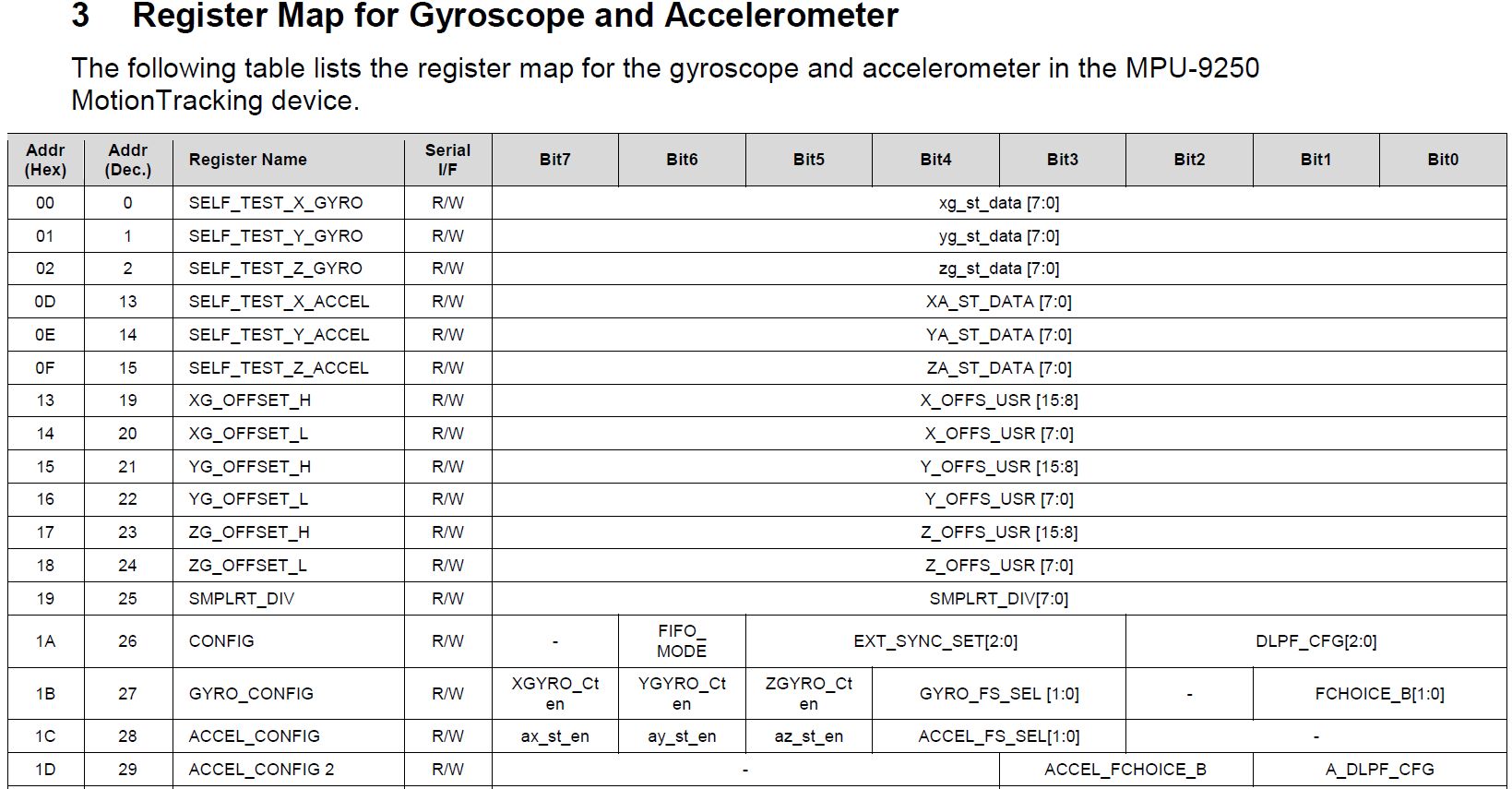
Dengan mengabaikan detail teknis konfigurasi, berikut ini dapat dikatakan. Pada sensor ini, pemfilteran bacaan yang dapat disesuaikan tidak hanya dari akselerometer, giroskop, tetapi juga sensor suhu dilakukan. Untuk masing-masing, ada total 7 hingga 10 mode, ditandai dengan konsep-konsep seperti Bandwidth dalam Hz, keterlambatan dalam ms, frekuensi sampling (Fs) dalam kHz.



Kolom "Noise Density" di $$$\ mu g / rtHz = \ mu g / \ sqrt {Hz}$ , dan kolom "Bandwidth" dilengkapi dengan nilai "3dB".



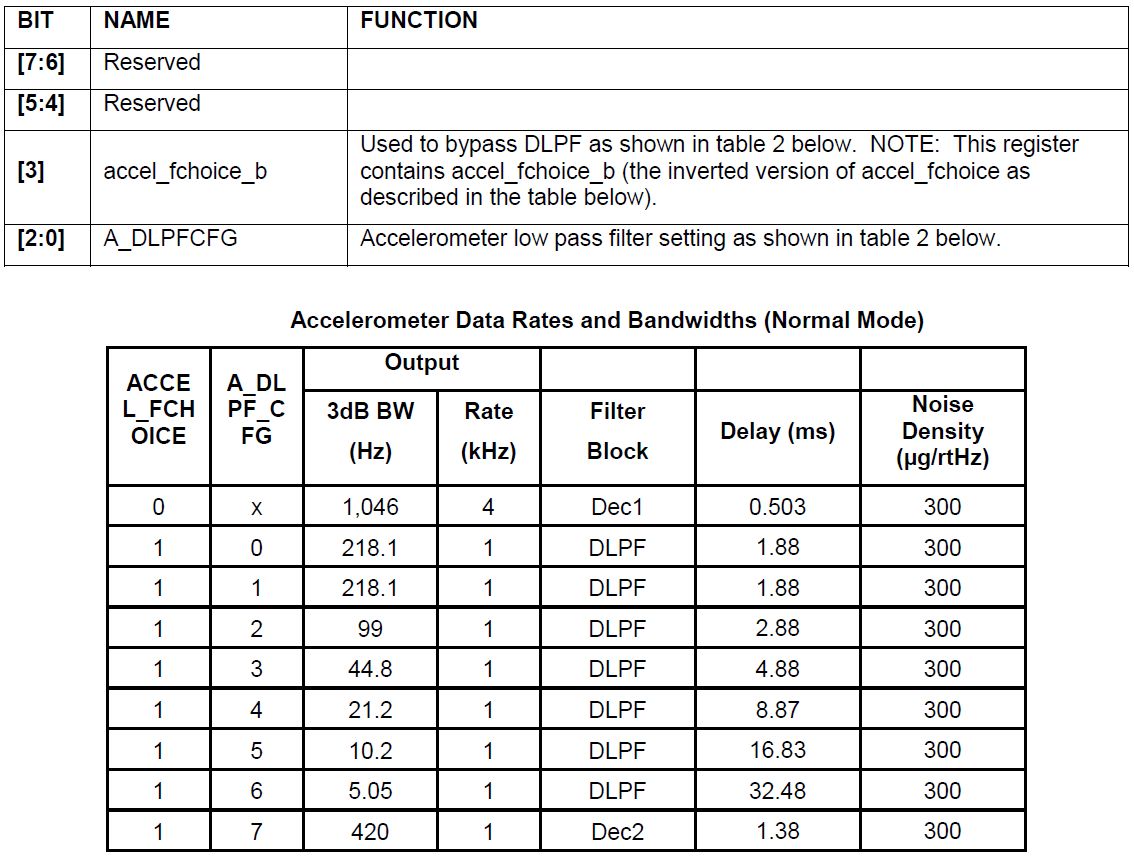
Itu tidak mudah, jadi mari kita langsung melihat daftar.

Warisan roma kuno

Tingkat Sampling + Desimasi $$$\ Delta \ Sigma$ ADC = laju data keluaran digital (ODR)

Dengan frekuensi pengambilan sampel (ini adalah frekuensi pengambilan sampel), semuanya jelas - ini adalah jumlah titik dari sinyal kontinu waktu yang diambil per detik selama pengambilan sampel oleh ADC. Diukur dalam hertz.

$$

$$Fs = \ frac {1} {\ delta t}$$

Untuk mendapatkan nilai yang mendekati amplitudo puncak sinyal, penting untuk mengambil frekuensi sampling setidaknya 10 kali frekuensi sinyal yang berguna. MPU-9250 menawarkan tiga opsi: Fs = 32kHz, 8kHz, 1kHz.

Tetapi ini sama sekali tidak berarti bahwa sinyal pada keluaran akselerometer atau giroskop muncul dengan periode yang sama.

Jika Anda menggunakan drone yang sama, maka semuanya bertumpu pada perjuangan untuk mengurangi konsumsi energi, meningkatkan kecepatan perhitungan dan mengurangi kebisingan data output. Anda dapat mengurangi frekuensi memperbarui data output dengan memungkinkan algoritma internal untuk mengintegrasikan informasi input selama periode waktu tertentu. Nilai RMS akan berkurang, tetapi bandwidth juga akan menyempit (sensor hanya dapat mendeteksi proses-proses yang frekuensinya akan kurang dari 50% dari laju pembaruan data).

Di sini lebih baik untuk mengingat teorema Kotelnikov segera. Dia berjanji bahwa ketika mengambil sampel sinyal analog, kehilangan informasi dapat dihindari (yaitu, mengembalikan sinyal tanpa distorsi) jika frekuensi sinyal yang berguna tidak lebih dari setengah frekuensi pengambilan sampel, juga disebut frekuensi Nyquist . Dalam praktiknya, filter anti-aliasing klasik (filter low-pass yang mengurangi kontribusi komponen frekuensi sekunder dalam sinyal output ke level yang dapat diabaikan - GOST R 8.714-2010) dalam banyak kasus memerlukan perbedaan setidaknya 2,5 kali [Siemens].

Untuk Fs = 32kHz, frekuensi Nyquist akan menjadi 16kHz. Pada saat yang sama, sinyal yang berguna tidak mungkin melampaui band fa = 20Hz (beberapa dapat mengubah arah pergerakan lebih dari 20 kali per detik). Secara total, frekuensi pengambilan sampel secara signifikan lebih tinggi daripada frekuensi yang diperlukan untuk menyimpan informasi yang terkandung dalam pita fa (40Hz, 400 kali lebih tinggi), yaitu, sinyal yang berguna oversampled. Pita antara frekuensi fa dan fs-fa tidak mengandung informasi yang berguna. Anda dapat mengurangi laju pengambilan sampel (dalam diagram ini dilakukan dengan koefisien M, [7]) dengan menipiskan urutan sampel (sampel). Proses ini disebut penipisan .



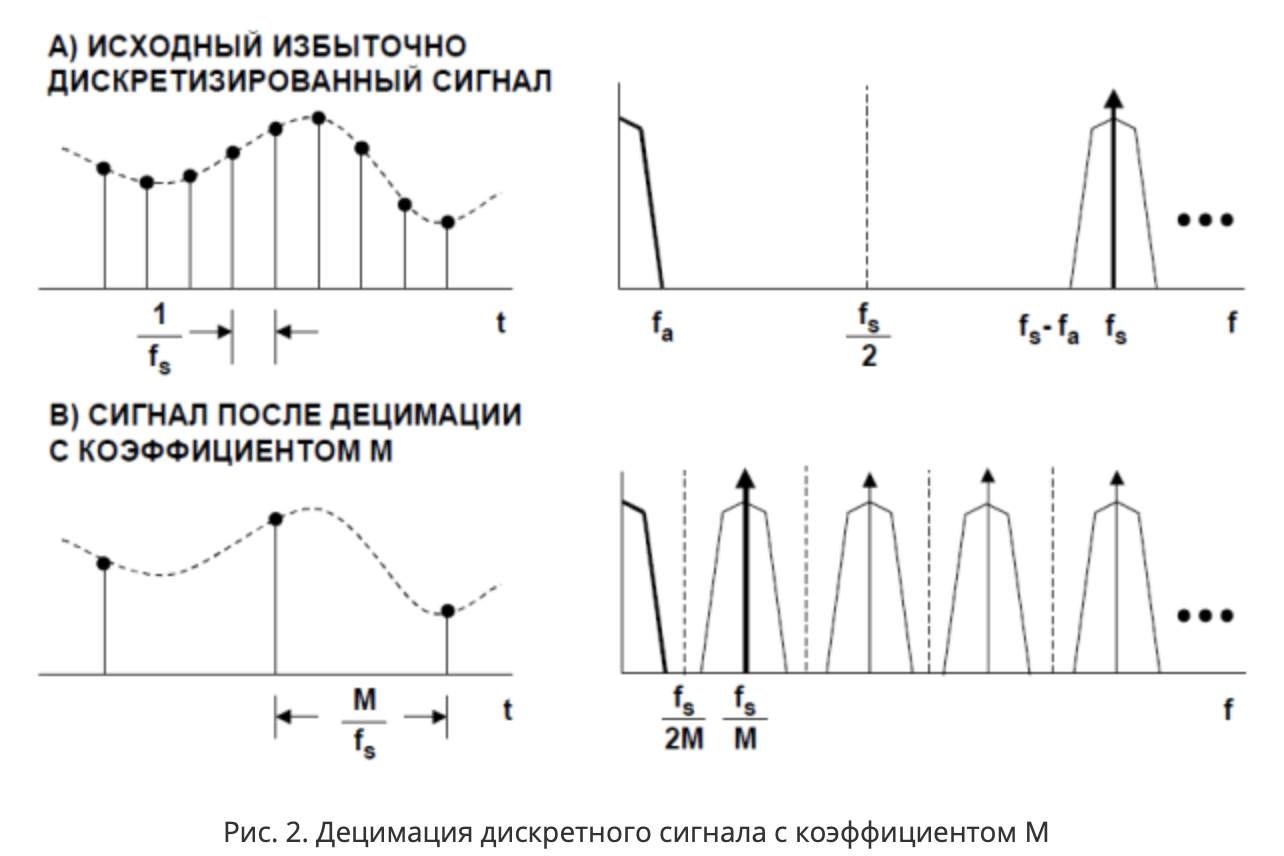
Menurut spesifikasi pada MPU-9250, accelerometer dilengkapi dengan sigma-delta ADC . Skema berdasarkan itu mengkonsumsi daya minimal. Perlu dicatat bahwa bandwidth dari konverter ini sangat sempit, tidak melebihi kisaran suara [Easyelectronics], tetapi untuk quadrocopter standar lebih banyak tidak diperlukan. Mereka terdiri dari dua blok: $$$\ Sigma \ Delta$ -modulator dan filter low-pass penipisan digital.

Mengapa menggabungkan low pass filter dan decimation?

Kutipan Jujur dari Wiki:

Jika sinyal sumber tidak mengandung frekuensi yang lebih tinggi dari frekuensi Nyquist dari sinyal terurai, maka bentuk spektrum dari sinyal yang diterima (terurai) bertepatan dengan bagian frekuensi rendah dari spektrum sinyal asli. Laju pengambilan sampel yang sesuai dengan urutan pengambilan sampel baru adalah N kali lebih rendah dari frekuensi pengambilan sampel dari sinyal asli.
Jika sinyal asli mengandung frekuensi yang lebih tinggi daripada frekuensi Nyquist dari sinyal yang dihancurkan, maka penghancuran akan menghasilkan aliasing (superposisi spektrum).

Dengan demikian, untuk mempertahankan spektrum, perlu, sebelum penghancuran, untuk menghapus dari frekuensi sinyal asli yang lebih tinggi dari frekuensi Nyquist dari sinyal yang dihancurkan. Spesifikasi MPU-9250 tidak mengandung banyak informasi tentang karakteristik DLPF, tetapi studi antusias dapat ditemukan [9].

Bandwidth, itu adalah respons frekuensi (respons frekuensi)

rentang frekuensi di mana sensor mendeteksi gerakan dan memberikan sinyal output yang valid. Dalam beberapa spesifikasi, respons frekuensi sensor diberikan - ketergantungan output listrik akselerometer pada tekanan mekanik eksternal dengan amplitudo tetap tetapi frekuensi berbeda. Di dalam bandwidth, ketidakrataan respon frekuensi tidak melebihi nilai yang diberikan. Dalam hal menggunakan filter low-pass digital, pilihan bandwidth hanya memungkinkan Anda untuk mengubah frekuensi cutoff, yang pasti mempengaruhi kecepatan respons sensor terhadap perubahan posisi di ruang. Frekuensi cutoff harus kurang dari setengah laju data keluaran digital (ODR), juga disebut frekuensi Nyquist.

Untuk akselerometer MPU-9250, batas bandwidth ditentukan sehingga dalam kisaran kerapatan spektral sinyal berbeda dari puncak (pada frekuensi 0 Hz) tidak lebih dari -3 dB. Level ini kira-kira setara dengan penurunan hingga setengah kepadatan spektral (atau 70,7% dari amplitudo spektral puncak). Biarkan saya mengingatkan Anda, untuk jumlah energi (daya, energi, kepadatan energi) sebanding dengan kuadrat kekuatan medan, dinyatakan dalam desibel, rasio

$$

$$D_P = 10 \ lg {P_2 \ lebih dari {P_1}}$$

.
Intinya: sinyal yang melewati filter low-pass kurang berisik, mereka memiliki resolusi yang lebih baik, tetapi lebih sedikit bandwidth. Oleh karena itu, menentukan resolusi dalam spesifikasi tanpa mengacu pada bandwidth tidak masuk akal.

Kembali ke resolusi

Dalam spesifikasi untuk MPU-9250, pada dasarnya tidak ada informasi tentang resolusi, untuk BMI088 dengan nama "Resolusi" resolusi digital (LSB) dan sensitivitas disajikan ":



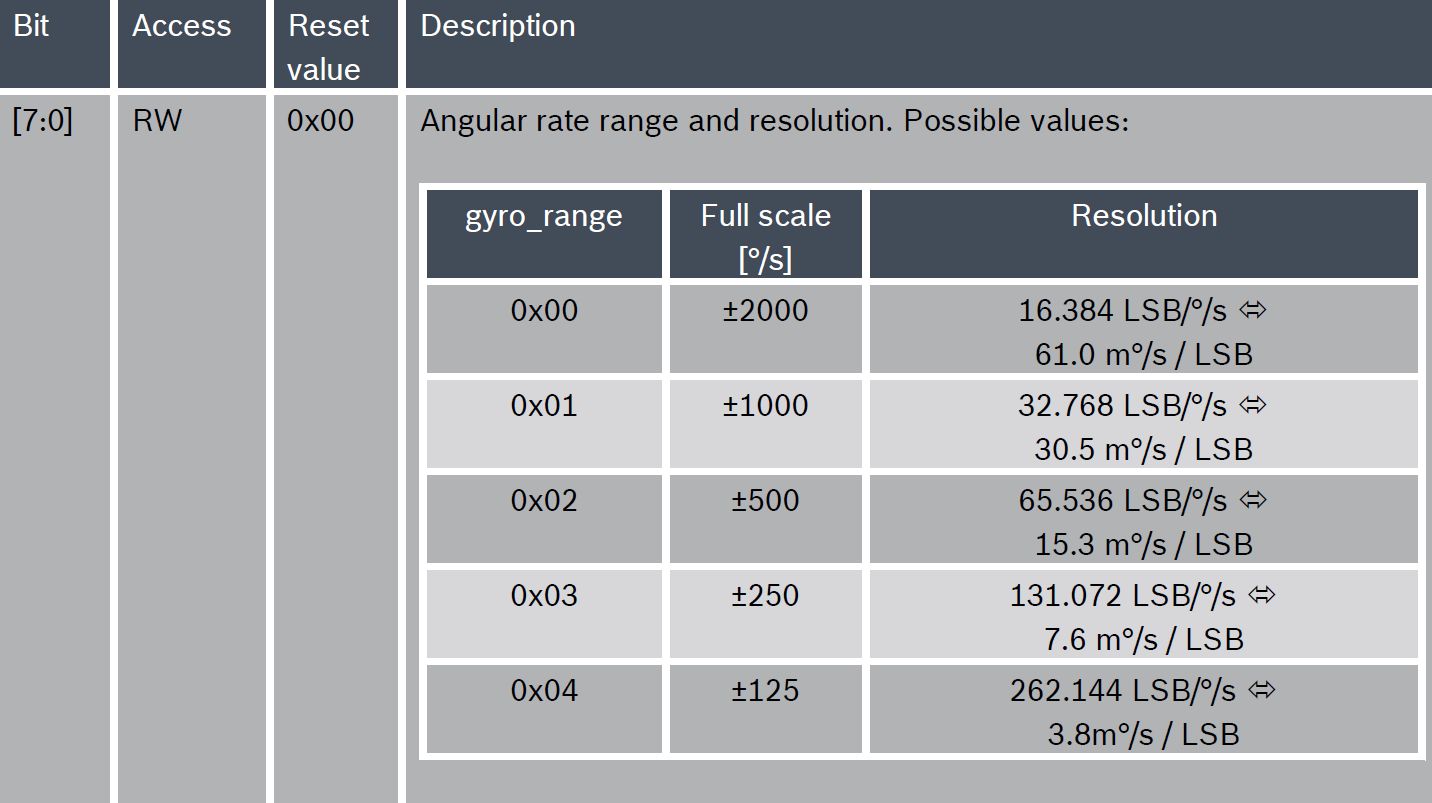
Resolusi untuk setiap bandwidth dapat diperkirakan dengan noise puncak. $$$Noise_ {pk-pk} = Total Noise_ {RMS} \ kali CrestFactor = Total Noise_ {RMS} \ kali 4.$ Nilai kuadrat akar rata-rata dari kebisingan pada output terkait dengan kepadatan spektral yang ditunjukkan dalam spesifikasi (atau lebih tepatnya, akar dari itu) dan bandwidth kebisingan setara (bandwidth kebisingan setara, ENBW) adalah bandwidth dari sistem yang setara yang memiliki respons frekuensi persegi panjang dan nilai yang sama pada frekuensi nol seperti sistem aslinya. dan dispersi pada output, ketika terpapar input dari sistem white noise):

$$

$$N_ {RMS} = PSD \ times \ sqrt {ENBW}$$

Dan bandwidth noise terhubung dengan band 3dB oleh koefisien yang sesuai dengan urutan filter low-pass:

$$

$$ENBW = 1.57 \ cdot f_ {3dB} \ textrm {untuk pesanan pertama}$$

$$

$$ENBW = 1.11 \ cdot f_ {3dB} \ textrm {untuk pesanan kedua}$$

$$

$$ENBW = 1.05 \ cdot f_ {3dB} \ textrm {untuk pesanan ketiga}$$

$$

$$ENBW = 1.025 \ cdot f_ {3dB} \ textrm {untuk pesanan keempat}$$

Dilihat oleh penelitian di [MPU9250_DLPF], pilihan kami adalah 1,57. Nilai rms yang diperoleh memperhitungkan kontribusi white noise (tidak ada noise kuantisasi atau noise mekanis di sana). Misalnya, untuk accelerometer, nilai yang dihitung untuk $$$BW = 99Hz, PSD = 300 \ mu g / \ sqrt {Hz}$ ternyata $$$N_ {RMS} = 4mg$ . Dalam hal ini, spesifikasinya berisi total kebisingan rms $$$Total RMS Noise = 8mg.$ Perbedaan itu signifikan. Sayangnya, hanya diindikasikan untuk satu band, dan untuk accelerometer BMI088, hanya PSD yang ditunjukkan dalam spesifikasi. Jadi kita akan menggunakan apa yang ada. Ambil faktor lintas 4. Sekarang yang paling menarik. Sikap $$$FS / Noise_ {pk-pk}$ akan memberikan urutan perkiraan bit efektif dalam rentang pengukuran ini, yang jauh lebih kecil dari resolusi 16-bit ADC.

MPU-9250			BMI088
Giroskop
$$$\ small N ^ {Total} _ {RMS} = 0,1 ^ {\ circ} / s (BW = 92Hz)$			$$$\ small N_ {RMS} = 0,1 ^ {\ circ} / s (BW = 47Hz)$
$$$\ small PSD = 0,01 ^ {\ circ} / s / \ sqrt {Hz}$			$$$\ small PSD = 0,014 ^ {\ circ} / s / \ sqrt {Hz}$
$$$\ BW kecil, Hz$	$$$\ small N_ {RMS}, ^ {\ circ} / s-rms$	$$$\ small N_ {PP}, ^ {\ circ} / s$	$$$\ BW kecil, Hz$	$$$\ small N_ {RMS}, ^ {\ circ} / s$	$$$\ small N_ {PP}, ^ {\ circ} / s$
			523	0,41	1.6
250	0,2	0.8	230	0,27	1.1
184	0,17	0,69	116	0,19	0,76
92	0,12	0,49	64	0,14	0,57
41	0,08	0,32	47	0,12	0,49
20	0,06	0,23	32	0,1	0,4
10	0,04	0,16	23	0,09	0,34
5	0,03	0,11	12	0,06	0,25
Akselerometer
$$$\ small N ^ {Total} _ {RMS} = 8mg \ textrm {(BW = 99Hz)}$			$$$\ small PSD_ {XY} = 160 \ mu g / \ sqrt {Hz}$
$$$\ small PSD = 300 \ mu g / \ sqrt {Hz} \ textrm {(Gyro off)}$			$$$\ small PSD_Z = 190 \ mu g / \ sqrt {Hz} (g_ {FS3g}, \ textrm {mode Normal})$
$$$\ BW kecil, Hz$	$$$\ small N_ {RMS}, mg$	$$$\ small N_ {PP}, mg$	$$$\ BW kecil, Hz$	$$$\ small N_ {RMS_XY}, mg$	$$$\ small N_ {PP_XY}, mg$
218.1	5.6	22	280	3.4	14
99	3.8	15	145	2.4	10
44.8	2.5	10	80	1.8	7
21.2	1.7	7	40	1.3	5
10.2	1.2	4.9	20	0,9	4
5.0	0,9	3.4	10	0,6	2.6
420	7.8	31	5	0,5	1.8
1046	12.3	49

Delay (ms), atau dari mana datangnya keterlambatan

Karena kebutuhan untuk menyimpan variabel dalam buffer internal untuk membagi sinyal dengan filter pada frekuensi yang berbeda

Total Semakin rendah frekuensi cutoff filter, semakin sedikit noise dalam sinyal. Tetapi di sini kita harus berhati-hati, karena pada saat yang sama penundaan bertambah. Selain itu, Anda dapat melewati sinyal yang berguna [8].

MPU-9250		BMI088
Giroskop, 16 bit
Rentang (FS) $$$^ {\ circ} / s$ (dps)	Resolusi, bit (BW = 92Hz)	Rentang (FS) $$$^ {\ circ} / s$ (dps)	Resolusi, bit (BW = 64Hz)
		$$$\ pm $ 12$	8
$$$\ pm $ 25$	9	$$$\ pm $ 25$	9
$$$\ pm $ 50$	10	$$$\ pm $ 50$	10
$$$\ pm $ 100$	11	$$$\ pm $ 100$	11
$$$\ pm $ 200$	12	$$$\ pm $ 200$	12
Akselerometer
Range (FS), g	Resolusi, sedikit $$$(N_ {PP} = 32mg)$	Range (FS), g	Resolusi (X, Y), sedikit $$$(N_ {PP} ^ XY = 14mg)$
$$$\ pm $$	6	$$$\ pm 3$	8
$$$\ pm $$	7	$$$\ pm $$	9
$$$\ pm 8$	8	$$$\ pm $ 1$	10
$$$\ pm 16$	9	$$$\ pm 24$	11

Dan ini hanyalah parameter paling dasar.

Dari mana datangnya:

1. Dokumen paling menyenangkan dari Freescale Semiconductor adalah "Berapa Banyak Bit yang Cukup?"
2. [EE] - “Resolusi vs Akurasi vs Sensitivitas Memotong Kebingungan”
3. [Waktu Elektronik] - “Sensor gerak MEMS dari STMicroelectronics: akselerometer dan giroskop”
4. [LSB] - “ADC dan DAC Least Significant Bit (LSB)”
5. [Pengukuran Komputasi] - “TechTip: Akurasi, Presisi, Resolusi, dan Sensitivitas”
6. [KIT] - “Accelerometer Perangkat Analog - Perangkat dan Aplikasi”
7. [Easyelectronics] - “Sigma-Delta ADC”
8. [Radiolotsman] - "Magnetometer: prinsip operasi, kompensasi kesalahan"
9. [SO] - “Pengukuran Kebisingan”
10. [Mide] - "Spesifikasi Accelerometer: Menguraikan Datasheet Accelerometer"
11. [CiberLeninka] - Delta-Sigma ADC Filter
12. [SciEd] - “Fitur implementasi penyaringan digital dengan perubahan frekuensi sampling”
13. [MPU6050] - “Menggunakan DLPF MPU6050”
14. [MPU9250_DLPF] - MPU9250 Gyro Noise DLPF investigasi kerja
15. Memahami Spesifikasi Resolusi Sensor
16. Pemrosesan Sinyal Digital Siemens
17. Sensor gerak MEMS dari STMicroelectronics
18. [TMWorld] - "Mengevaluasi unit pengukuran inersia"
19. [Sklyar] - Sklyar B. Komunikasi Digital. Fondasi teoretis dan penerapan praktis.