Latensi Belajar: Teori Antrian

Tema latensi dari waktu ke waktu menjadi menarik dalam sistem yang berbeda di Yandex dan tidak hanya. Ini terjadi karena jaminan layanan apa pun muncul di sistem ini. Jelas, faktanya adalah penting tidak hanya untuk menjanjikan beberapa peluang kepada pengguna, tetapi juga untuk menjamin penerimaannya dengan waktu respons yang masuk akal. "Rasionalitas" dari waktu respons, tentu saja, sangat bervariasi untuk sistem yang berbeda, tetapi prinsip-prinsip dasar dimana latensi dimanifestasikan dalam semua sistem adalah umum, dan mereka dapat dipertimbangkan secara terpisah dari spesifikasi.

Nama saya Sergey Trifonov, saya bekerja di tim Real-Time Map Reduce di Yandex. Kami sedang mengembangkan platform untuk pemrosesan aliran data waktu-nyata dengan waktu respons kedua dan kedua. Platform ini tersedia untuk pengguna internal dan memungkinkan mereka untuk mengeksekusi kode aplikasi pada aliran data yang masuk secara konstan. Saya akan mencoba memberikan ikhtisar singkat tentang konsep dasar umat manusia tentang topik analisis latensi selama seratus sepuluh tahun terakhir, dan sekarang kita akan mencoba memahami apa yang sebenarnya dapat dipelajari tentang latensi menggunakan teori antrian.

Fenomena latensi mulai diselidiki secara sistematis, sejauh yang saya tahu, sehubungan dengan munculnya sistem antrian - jaringan komunikasi telepon. Teori antrian dimulai dengan karya A.K. Erlang pada tahun 1909, di mana ia menunjukkan bahwa distribusi Poisson berlaku untuk lalu lintas telepon acak. Erlang mengembangkan teori yang telah digunakan selama beberapa dekade untuk merancang jaringan telepon. Teori ini memungkinkan kita untuk menentukan probabilitas penolakan layanan. Untuk jaringan telepon dengan saluran switch circuit, kegagalan terjadi jika semua saluran sibuk dan panggilan tidak dapat dilakukan. Peluang kejadian ini harus dikontrol. Saya ingin memiliki jaminan bahwa, misalnya, 95% dari semua panggilan akan dilayani. Rumus Erlang memungkinkan untuk menentukan berapa banyak server yang diperlukan untuk memenuhi jaminan ini jika durasi dan jumlah panggilan diketahui. Sebenarnya, tugas ini hanya tentang jaminan kualitas, dan saat ini orang masih menyelesaikan masalah serupa. Tetapi sistem menjadi jauh lebih kompleks. Masalah utama dari teori antrian adalah bahwa hal itu tidak diajarkan di sebagian besar institusi, dan hanya sedikit orang yang memahami pertanyaan di luar antrian M / M / 1 (lihat notasi di bawah ), tetapi diketahui bahwa hidup jauh lebih rumit daripada sistem ini. Karena itu, saya usulkan, melewati M / M / 1, langsung menuju yang paling menarik.

Nilai rata-rata

Jika Anda tidak mencoba untuk mendapatkan pengetahuan lengkap tentang distribusi probabilitas dalam sistem, tetapi fokus pada pertanyaan yang lebih sederhana, Anda bisa mendapatkan hasil yang menarik dan bermanfaat. Yang paling terkenal di antara mereka adalah, tentu saja, teorema Little . Ini berlaku untuk sistem dengan aliran input apa pun, perangkat internal kompleksitas apa pun, dan penjadwal sewenang-wenang di dalamnya. Satu-satunya persyaratan adalah bahwa sistem harus stabil: waktu respons rata-rata dan panjang antrian harus ada, kemudian mereka dihubungkan dengan ekspresi sederhana

$$

$$L = \ lambda W$$

dimana $$$L$ - jumlah waktu rata-rata permintaan di bagian sistem yang dianggap [pcs], $$$W$ - waktu rata-rata yang diminta melewati bagian sistem ini, $$$\ lambda$ - kecepatan penerimaan permintaan ke sistem [pcs / s]. Kekuatan teorema adalah bahwa ia dapat diterapkan ke bagian mana pun dari sistem: antrian, eksekutor, antrian + eksekutor, atau seluruh jaringan. Seringkali teorema ini digunakan kira-kira seperti ini: "Aliran 1Gbit / s mengalir ke kami, dan kami mengukur waktu respons rata-rata, dan itu adalah 10 ms, oleh karena itu, rata-rata kami memiliki 1,25 MB dalam penerbangan." Jadi, perhitungan ini tidak benar. Lebih tepatnya, itu benar hanya jika semua permintaan memiliki ukuran yang sama dalam byte. Teorema kecil menghitung kueri dalam potongan, bukan dalam byte.

Cara menggunakan teorema Little

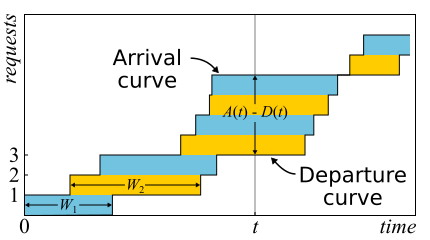
Dalam matematika, seringkali perlu untuk mempelajari bukti untuk mendapatkan wawasan yang nyata. Inilah masalahnya. Teorema Little sangat bagus sehingga saya memberikan sketsa buktinya di sini. Lalu lintas masuk dijelaskan oleh fungsi $$$A (t)$ - jumlah permintaan yang masuk pada saat itu $$$t$ . Begitu pula $$$D (t)$ - jumlah permintaan yang keluar saat itu $$$t$ . Momen masuk (keluar) dari permintaan dianggap sebagai momen penerimaan (pengiriman) dari byte terakhirnya. Batas-batas sistem hanya ditentukan oleh contoh waktu ini, oleh karena itu, teorema ini berlaku luas. Jika Anda menggambar grafik fungsi-fungsi ini dalam sumbu yang sama, mudah untuk melihatnya $$$A (t) - D (t)$ Apakah jumlah permintaan dalam sistem pada waktu t, dan $$$W_n$ - waktu respons permintaan ke-n.

Teorema itu secara formal terbukti hanya pada tahun 1961, meskipun hubungan itu sendiri sudah diketahui jauh sebelum itu.

Bahkan, jika permintaan dapat disusun kembali dalam sistem, maka semuanya sedikit lebih rumit, jadi untuk kesederhanaan kita akan menganggap bahwa ini tidak terjadi. Meskipun teorema itu benar dalam kasus ini juga. Sekarang mari kita menghitung area di antara grafik. Ada dua cara untuk melakukan ini. Pertama, menurut kolom - sebagai integral biasanya berpikir. Dalam hal ini, ternyata integand adalah ukuran antrian yang terpotong-potong. Kedua, baris demi baris - cukup tambahkan latensi semua permintaan. Jelas bahwa kedua perhitungan memberikan area yang sama, oleh karena itu keduanya sama. Jika kedua bagian dari kesetaraan ini dibagi dengan waktu Δt, yang kami hitung luasnya, maka di sebelah kiri kami akan memiliki panjang antrian rata-rata $$$L$ (dengan definisi rata-rata). Di sebelah kanan sedikit lebih rumit. Kita perlu menambahkan sejumlah permintaan N ke pembilang dan penyebut, maka kita akan berhasil

$$

$$\ frac {\ sum W_i} {\ Delta t} = \ frac {\ sum W_i} {N} \ frac {N} {\ Delta t} = W \ lambda$$

Jika kita mempertimbangkan Δt atau periode kerja yang cukup besar, maka pertanyaan di tepi dihapus dan teorema dapat dianggap terbukti.

Penting untuk mengatakan bahwa dalam bukti kami tidak menggunakan distribusi probabilitas apa pun. Faktanya, teorema Little adalah hukum deterministik! Undang-undang semacam itu disebut dalam teori antrian hukum operasional. Mereka dapat diterapkan ke bagian mana saja dari sistem dan distribusi dari berbagai variabel acak. Undang-undang ini membentuk konstruktor yang dapat berhasil digunakan untuk menganalisis nilai rata-rata di jaringan. Kerugiannya adalah semuanya hanya berlaku untuk rata-rata dan tidak memberikan pengetahuan tentang distribusi.

Kembali ke pertanyaan mengapa teorema Little tidak dapat diterapkan pada byte, anggaplah itu $$$A (t)$ dan $$$D (t)$ sekarang mereka diukur bukan dalam potongan, tetapi dalam byte. Kemudian, dengan melakukan argumen yang sama, kita mendapatkan sebaliknya $$$W$ yang aneh adalah area dibagi dengan jumlah total byte. Ini masih beberapa detik, tetapi ini adalah latensi rata-rata tertimbang di mana permintaan yang lebih besar mendapatkan lebih banyak bobot. Nilai ini dapat disebut latensi rata-rata byte - yang, secara umum, logis, karena kami mengganti potongan-potongan dengan byte - tetapi bukan latensi permintaan.

Teorema Little mengatakan bahwa dengan aliran permintaan tertentu, waktu respons dan jumlah permintaan dalam sistem proporsional. Jika semua permintaan terlihat sama, maka waktu respons rata-rata tidak dapat dikurangi tanpa meningkatkan daya. Jika kami mengetahui ukuran kueri sebelumnya, kami dapat mencoba menyusun ulang di dalamnya untuk mengurangi area di antaranya $$$A (t)$ dan $$$D (t)$ dan karenanya waktu respons sistem rata-rata. Melanjutkan ide ini, kami dapat membuktikan bahwa algoritma Waktu Proses Tersingkat dan Waktu Proses Tersingkat terpendek memberikan rata-rata waktu respons rata-rata untuk satu server tanpa kemungkinan saling berkutat dengannya. Tetapi ada efek samping - permintaan besar mungkin tidak diproses tanpa batas waktu. Fenomena ini disebut "kelaparan" dan terkait erat dengan konsep keadilan perencanaan, yang dapat dipelajari dari posting Penjadwalan sebelumnya : mitos dan kenyataan .

Ada jebakan umum lainnya yang terkait dengan memahami hukum Little. Ada server berulir tunggal yang melayani permintaan pengguna. Misalkan kita entah bagaimana mengukur L - jumlah rata-rata permintaan dalam antrian untuk server ini, dan S - rata-rata waktu server melayani satu permintaan. Sekarang pertimbangkan permintaan masuk baru. Rata-rata, dia melihat L bertanya di depannya. Melayani mereka masing-masing membutuhkan rata-rata S detik. Ternyata waktu tunggu rata-rata $$$W = L S$ . Tapi menurut teorema ternyata itu $$$W = L / \ lambda$ . Jika kita menyamakan ekspresi, maka kita melihat omong kosong: $$$S = 1 / \ lambda$ . Apa yang salah dengan alasan ini?

1. Hal pertama yang menarik perhatian Anda: waktu respons oleh teorema tidak bergantung pada S. Bahkan, tentu saja, itu tergantung. Hanya saja, panjang antrian rata-rata sudah memperhitungkan hal ini: semakin cepat server, semakin pendek antrian, dan semakin pendek waktu respons.
2. Kami menganggap sistem di mana antrian tidak menumpuk selamanya, tetapi secara teratur direset. Ini berarti bahwa pemanfaatan server kurang dari 100% dan kami melewatkan semua permintaan yang masuk, dan pada kecepatan rata-rata yang sama dengan saat permintaan ini tiba, yang berarti rata-rata tidak membutuhkan S detik, tetapi lebih, untuk memproses satu permintaan $$$1 / \ lambda$ detik, hanya karena kadang-kadang kami tidak memproses permintaan apa pun. Faktanya adalah bahwa dalam sistem terbuka yang stabil tanpa kehilangan, throughput tidak tergantung pada kecepatan server, itu hanya ditentukan oleh aliran input.
3. Asumsi bahwa permintaan masuk melihat dalam sistem jumlah waktu rata-rata permintaan tidak selalu benar. Contoh tandingan: permintaan masuk datang secara berkala, dan kami berhasil memproses setiap permintaan sebelum permintaan berikutnya datang. Gambaran umum untuk sistem waktu nyata. Permintaan yang masuk selalu melihat nol permintaan dalam sistem, tetapi rata-rata sistem jelas memiliki lebih dari nol permintaan. Jika permintaan datang pada waktu yang benar-benar acak, maka mereka benar-benar "melihat jumlah rata-rata permintaan . "
   
   
   
4. Kami tidak memperhitungkan bahwa dengan probabilitas tertentu mungkin sudah ada satu permintaan di server yang perlu "diperluas". Dalam kasus umum, waktu rata-rata “after-service” berbeda dari waktu awal layanan, dan kadang-kadang, secara paradoksal , itu bisa berubah menjadi lebih lama. Kami akan kembali ke masalah ini di akhir ketika kita membahas microbursts, tetap disini.

Jadi, teorema Little dapat diterapkan pada sistem besar dan kecil, ke antrian, ke server, dan ke utas pemrosesan tunggal. Tetapi dalam semua kasus ini, permintaan biasanya diklasifikasikan dalam satu atau lain cara. Permintaan pengguna yang berbeda, permintaan prioritas yang berbeda, permintaan yang datang dari lokasi yang berbeda, atau permintaan dari jenis yang berbeda. Dalam hal ini, informasi yang dikumpulkan oleh kelas tidak menarik. Ya, jumlah rata-rata permintaan campuran dan waktu respons rata-rata untuk semua permintaan tersebut kembali proporsional. Tetapi bagaimana jika kita ingin mengetahui waktu respons rata-rata untuk kelas permintaan tertentu? Anehnya, teorema Little dapat diterapkan ke kelas kueri tertentu. Dalam hal ini, Anda harus menganggapnya sebagai $$$\ lambda$ Tingkat permintaan kelas ini, tidak semua. Sebagai a $$$L$ dan $$$W$ - nilai rata-rata jumlah dan waktu tinggal permintaan kelas ini di bagian sistem yang diselidiki.

Sistem terbuka dan tertutup

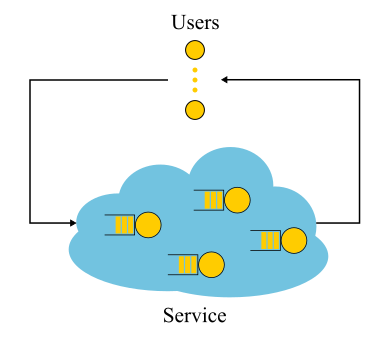
Perlu dicatat bahwa untuk sistem tertutup garis pemikiran yang "salah" mengarah pada kesimpulan $$$S = 1 / \ lambda$ ternyata benar. Sistem tertutup adalah sistem di mana permintaan tidak datang dari luar dan tidak keluar, tetapi beredar di dalam. Atau, jika tidak, sistem umpan balik: begitu permintaan meninggalkan sistem, permintaan baru menggantikannya. Sistem ini juga penting karena setiap sistem terbuka dapat dianggap terbenam dalam sistem tertutup. Misalnya, Anda dapat mempertimbangkan situs sebagai sistem terbuka, di mana permintaan terus-menerus dituangkan, diproses dan ditarik, atau, sebaliknya, sebagai sistem tertutup dengan seluruh audiens situs. Kemudian mereka biasanya mengatakan bahwa jumlah pengguna sudah diperbaiki, dan mereka menunggu jawaban untuk permintaan atau "berpikir": mereka menerima halaman mereka dan belum mengklik tautan tersebut. Jika waktu berpikir selalu nol, sistem ini juga disebut sistem batch.

Hukum Little untuk sistem tertutup valid jika kecepatan kedatangan eksternal $$$\ lambda$ (mereka tidak berada dalam sistem tertutup) ganti dengan bandwidth sistem. Jika kita membungkus server single-threaded yang dibahas di atas dalam sistem batch, kita dapatkan $$$S = 1 / \ lambda$ dan 100% daur ulang. Seringkali pandangan seperti itu pada sistem memberikan hasil yang tidak terduga. Pada tahun 90-an, justru pandangan tentang Internet ini bersama-sama dengan pengguna sebagai satu sistem tunggal yang memberikan dorongan untuk mempelajari distribusi selain eksponensial. Kami akan membahas distribusi lebih lanjut, tetapi di sini kami mencatat bahwa pada waktu itu hampir semua dan di mana-mana dianggap sebagai eksponensial, dan ini bahkan ditemukan beberapa pembenaran, dan bukan hanya alasan dalam semangat "kalau tidak terlalu rumit." Namun, ternyata tidak semua distribusi yang penting praktis memiliki ekor yang sama panjangnya, dan pengetahuan tentang ekor distribusi dapat dicoba. Tetapi untuk sekarang, mari kita kembali ke nilai rata-rata.

Efek relativistik

Misalkan kita memiliki sistem terbuka: jaringan yang kompleks atau server single-threaded sederhana - tidak masalah. Apa yang akan berubah jika kita menggandakan kedatangan permintaan dan mempercepat pemrosesan mereka setengah - misalnya, dengan menggandakan kapasitas semua komponen sistem? Bagaimana pemanfaatan, throughput, jumlah rata-rata permintaan dalam sistem dan waktu respons rata-rata berubah? Untuk server single-threaded, Anda dapat mencoba mengambil formula, menerapkannya "di dahi" dan mendapatkan hasilnya, tetapi apa yang harus dilakukan dengan jaringan yang sewenang-wenang? Solusi intuitif adalah sebagai berikut. Misalkan waktu digandakan, maka dalam "sistem referensi dipercepat" kami kecepatan server dan aliran permintaan sepertinya tidak berubah; karenanya, semua parameter dalam waktu dipercepat memiliki nilai yang sama seperti sebelumnya. Dengan kata lain, akselerasi semua "bagian yang bergerak" dari sistem apa pun setara dengan akselerasi jam. Sekarang kita akan mengonversi nilai ke sistem dengan waktu normal. Jumlah tak berdimensi (pemanfaatan dan jumlah rata-rata permintaan) tidak akan berubah. Nilai yang dimensinya mencakup faktor-faktor waktu dari tingkat pertama bervariasi secara proporsional. Throughput [permintaan / s] akan berlipat ganda, dan waktu respons dan waktu tunggu akan dikurangi setengahnya.

Hasil ini dapat diartikan dengan dua cara:

1. Suatu sistem yang dipercepat oleh k kali dapat mencerna aliran tugas k kali lebih banyak, dan dengan waktu respons rata-rata k kali lebih sedikit.
2. Kita dapat mengatakan bahwa daya tidak berubah, tetapi hanya ukuran tugas berkurang k kali. Ternyata kami mengirim beban yang sama ke sistem, tetapi digergaji dalam potongan yang lebih kecil. Dan ... oh, keajaiban! Waktu respons rata-rata berkurang!

Sekali lagi, saya perhatikan bahwa ini berlaku untuk kelas sistem yang luas, dan bukan hanya untuk server sederhana. Dari sudut pandang praktis, hanya ada dua masalah:

1. Tidak semua bagian sistem dapat dipercepat dengan mudah. Kami tidak bisa memengaruhi beberapa orang sama sekali. Misalnya, kecepatan cahaya.
2. Tidak semua tugas dapat dibagi secara tak terbatas menjadi yang lebih kecil dan lebih kecil, karena informasi belum dipelajari untuk ditransfer dalam porsi kurang dari satu bit.

Pertimbangkan perikop sampai batasnya. Misalkan, dalam sistem terbuka yang sama, interpretasi No. 2. Kami membagi setiap permintaan masuk menjadi dua. Waktu respons juga dibagi dua. Ulangi pembagian ini berkali-kali. Dan kita bahkan tidak perlu mengubah apa pun dalam sistem. Ternyata Anda dapat membuat waktu respons menjadi kecil secara sewenang-wenang hanya dengan melihat permintaan masuk menjadi sejumlah besar bagian. Dalam batasnya, kita dapat mengatakan bahwa alih-alih kueri, kita mendapatkan "cairan permintaan", yang kami filter oleh server kami. Inilah yang disebut model fluida, alat yang sangat mudah untuk analisis yang disederhanakan. Tetapi mengapa waktu respon nol? Apa yang salah? Di mana kami tidak mempertimbangkan latensi? Ternyata kami tidak memperhitungkan hanya kecepatan cahaya, itu tidak bisa digandakan. Waktu propagasi dalam saluran jaringan tidak dapat diubah, Anda hanya dapat bertahan dengan itu. Bahkan, transmisi melalui jaringan mencakup dua komponen: waktu transmisi dan waktu propagasi. Yang pertama dapat dipercepat dengan meningkatkan daya (lebar saluran) atau mengurangi ukuran paket, dan yang kedua sangat sulit untuk dipengaruhi. Dalam "model cairan" kami, tidak ada reservoir untuk akumulasi cairan - saluran jaringan dengan waktu propagasi non-nol dan konstan. Ngomong-ngomong, jika kita menambahkannya ke "model cair" kita, latensi akan ditentukan oleh jumlah waktu propagasi, dan antrian dalam node masih kosong. Antrian hanya bergantung pada ukuran paket dan variabilitas (baca burst) dari aliran input.

Oleh karena itu ketika datang ke latensi, Anda tidak bisa bertahan dengan perhitungan arus, dan bahkan perangkat daur ulang tidak menyelesaikan semuanya. Penting untuk mempertimbangkan ukuran permintaan dan tidak melupakan waktu distribusi, yang sering diabaikan dalam teori antrian, meskipun menambahkannya ke dalam perhitungan sama sekali tidak sulit.

Distribusi

Apa alasan antrian? Jelas, sistem tidak memiliki kapasitas yang cukup, dan kelebihan permintaan terakumulasi? Tidak benar Antrian juga muncul dalam sistem di mana ada sumber daya yang cukup. Jika tidak ada kapasitas yang cukup, maka sistem, seperti yang dikatakan oleh ahli teori, tidak stabil. Ada dua alasan utama untuk antri: ketidakteraturan permintaan dan variabilitas ukuran permintaan. Kami telah memeriksa contoh di mana kedua alasan ini telah dieliminasi: sistem waktu nyata di mana permintaan dengan ukuran yang sama datang secara ketat secara berkala. Antrian tidak pernah terbentuk. Waktu tunggu rata-rata dalam antrian adalah nol. , , , . , .

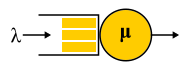
A/S/k/K, A — , S — , k — , K — (, ). , M/M/1 : M (Markovian Memoryless) , . : $$$\lambda$ — — , : . M , μ . , , . , 4- . , , : G — (, , ), D — deterministic. C — D/D/1. , 1909 ., — M/D/1. — M/G/k k>1, M/G/1 1930-.

?

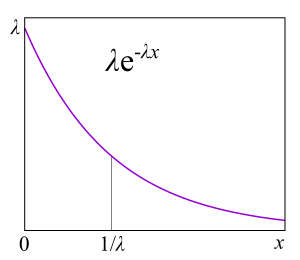
, , , , , . , . , failure rate . , , : , . failure rate function, . , «» , . , : , . , failure rate — , , - , — . , , , , , . « ».

Failure rate . — . Failure rate , , , . failure rate, , , . failure rate, , , . , , , software hardware? : ? . , , - . ? , — . ( failure rate) . « » .

, , failure rate, , , unix- . , .

RTMR , . LWTrace - . . , . , $$$\mathbf{P}\{S>x\}$ . , failure rate , , : .



$$$\mathbf{P}\{S>x\} = x^{-a}$ , — . , « », 80/20: , . . , . , RTMR -, , . $$$a=1.16$ , 80/20: 20% 80% .

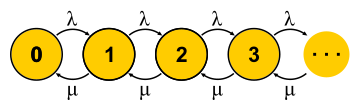
, . . , , , - . , — . « » , « » — . : , ? , ( , ), . , 0 . , , $$$\mu N_1$ $$$\lambda N_0$ . , , — . . , . M/M/1 $$$\mathbf{P}\{Q=i\} = (1 - \rho) \rho^i$ dimana $$$\rho = \lambda / \mu$ - Ini adalah pemanfaatan server. Akhir dari cerita. Dalam perjalanan presentasi, saya melewatkan sejumlah asumsi yang layak dan membuat beberapa pergantian konsep, tetapi esensinya, saya harap, tidak menderita.

Penting untuk dipahami bahwa pendekatan ini hanya berfungsi jika keadaan mesin saat ini sepenuhnya menentukan perilaku selanjutnya, dan kisah bagaimana ia masuk ke keadaan ini tidak penting. Untuk pemahaman sehari-hari tentang mesin negara yang terbatas, ini tidak perlu dikatakan lagi - bagaimanapun, ini adalah kondisi untuk itu. Tetapi untuk proses stokastik, ini mengikuti dari ini bahwa semua distribusi harus eksponensial, karena hanya mereka tidak memiliki memori - mereka memiliki tingkat kegagalan yang konstan.

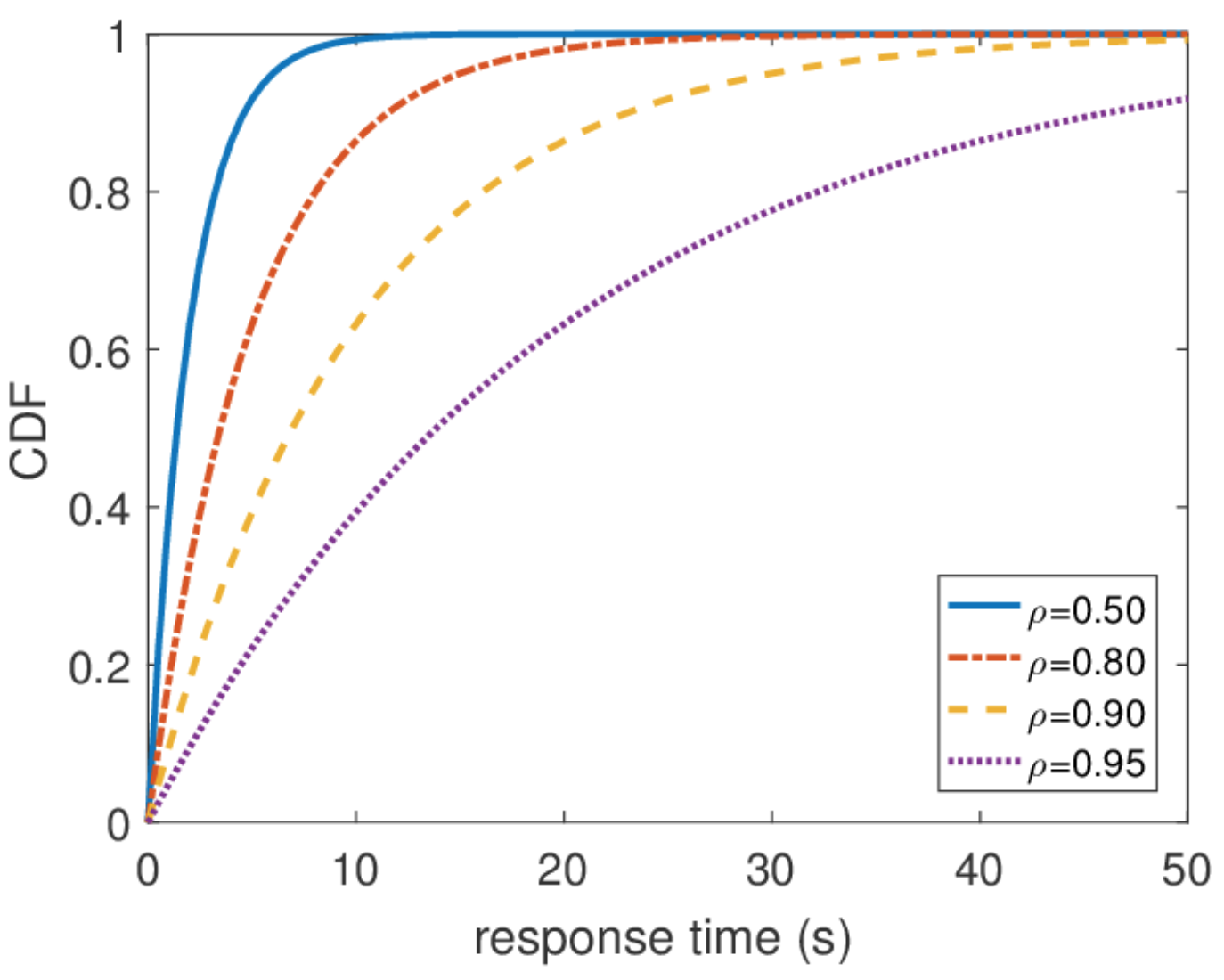
Penting juga untuk mengatakan bahwa semua informasi lain tentang sistem mudah diperoleh jika kita mengetahui distribusi kesetimbangan. Jumlah rata-rata kueri dalam sistem adalah rata-rata dari distribusi ini. Untuk mengetahui waktu respons rata-rata, kami menerapkan teorema Little ke jumlah kueri. Distribusi waktu respons sedikit lebih sulit ditemukan, tetapi juga dalam beberapa tindakan Anda dapat mengetahuinya $$$\ mathbf {P} \ {response \ _time> t \} = e ^ {- (\ mu- \ lambda) t}$ dan berapa waktu respon rata-rata $$$1 / (\ mu- \ lambda)$ .

Waktu respons tidak terbatas

Dari distribusi ini, Anda dapat menemukan persentil apa pun dari waktu respons, dan ternyata persentil ke-seratus sama dengan tak terhingga. Dengan kata lain, waktu respons terburuk tidak terbatas dari atas. Yang, secara umum, tidak mengejutkan, karena kami menggunakan aliran Poisson. Namun dalam praktiknya, perilaku seperti itu tidak pernah bisa dipenuhi. Jelas, aliran input permintaan ke server terbatas, setidaknya oleh lebar saluran jaringan ke server ini, dan panjang antrian dibatasi oleh memori di server ini. Aliran Poisson, sebaliknya, dengan probabilitas non-nol menjamin terjadinya semburan besar yang sewenang-wenang. Oleh karena itu, saya tidak akan merekomendasikan melanjutkan dari asumsi aliran input Poisson ketika merancang suatu sistem jika Anda tertarik pada persentil tinggi dan beban sistem sangat tinggi. Lebih baik menggunakan model lalu lintas lain, yang akan saya bicarakan di lain waktu ketika saya akan berbicara tentang kalkulus jaringan.

Penskalaan dan Jaminan

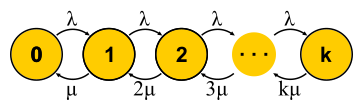
Sekarang kita memiliki cara yang cukup kuat untuk menganalisis sistem, kita dapat mencoba menerapkannya pada tugas yang berbeda dan menuai manfaatnya. Inilah bagaimana teori pelayanan massa dikembangkan pada paruh kedua abad kedua puluh. Mari kita coba memahami apa yang telah dicapai. Untuk memulainya, mari kita kembali ke tugas yang diselesaikan Erlang. Ini adalah tugas M / M / k / k dan M / M / k, di mana kami ingin membatasi probabilitas kegagalan. Ternyata tidak sulit bagi mereka untuk membangun rantai Markov. Perbedaannya adalah bahwa ketika tugas ditambahkan, kemungkinan transisi balik meningkat, karena tugas mulai diproses secara paralel, tetapi ketika jumlah tugas menjadi sama dengan jumlah server, terjadi kejenuhan. Selanjutnya, untuk M / M / k / k, jaringan berakhir, otomat benar-benar menjadi terbatas, dan semua permintaan yang datang ke keadaan terakhir ditolak. Probabilitas peristiwa ini sama dengan probabilitas bahwa kita berada dalam keadaan terakhir.

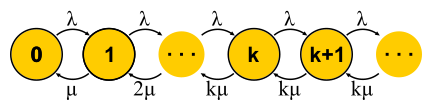
Untuk M / M / k, situasinya lebih rumit, permintaan antri, status baru muncul, tetapi kemungkinan transisi balik tidak meningkat - semua server sudah berfungsi. Jaringan menjadi tidak terbatas, seperti untuk M / M / 1. By the way, jika jumlah permintaan dalam sistem terbatas, maka rantai akan selalu memiliki jumlah negara yang terbatas dan satu atau lain cara itu akan diselesaikan, yang tidak dapat dikatakan tentang rantai tanpa akhir. Dalam sistem tertutup, rantai selalu terbatas. Memecahkan sirkuit yang dijelaskan untuk M / M / k / k dan M / M / k, kita tiba di rumus B dan rumus Erlang C, masing-masing. Mereka agak besar, saya tidak akan memberi mereka, tetapi dengan bantuan mereka, Anda bisa mendapatkan hasil yang menarik untuk pengembangan intuisi, yang disebut aturan staf akar kuadrat. Misalkan ada sistem M / M / k dengan beberapa aliran input yang diberikan λ dari permintaan per detik. Misalkan bebannya akan berlipat ganda besok. Pertanyaannya adalah: bagaimana cara menambah jumlah server sehingga waktu responsnya tetap sama? Jumlah server harus digandakan, kan? Ternyata tidak sama sekali. Ingat bahwa kita telah melihat: jika Anda mempercepat waktu (server dan login) setengahnya, maka waktu respons rata-rata berkurang setengahnya. Beberapa server yang lambat dan satu yang cepat bukan hal yang sama, tetapi daya komputasi tetap sama. Khususnya, untuk M / M / 1, misalnya, waktu respons berbanding terbalik dengan volume “kapasitas bebas” $$$\ mu - \ lambda$ dan hanya ditentukan oleh volume ini. Saat menggandakan aliran dan daya pemrosesan, kapasitas bebas sistem berlipat ganda: $$$2 \ mu - 2 \ lambda$ . Tampaknya untuk menyelesaikan masalah Anda hanya perlu menghemat kapasitas gratis, tetapi waktu respons dalam M / M / k sudah ditentukan oleh rumus Erlang yang lebih kompleks. Ternyata kapasitas bebas harus dipertahankan sebanding dengan akar kuadrat dari jumlah "server sibuk" untuk mempertahankan waktu respons yang sama. Dengan jumlah "server sibuk" berarti jumlah total server dikalikan dengan pemanfaatan: ini adalah jumlah minimum server yang diperlukan untuk operasi yang stabil.

Menggunakan aturan ini, kadang-kadang mereka mencoba membenarkan cara memperluas cluster dengan server. Tetapi jangan berada di bawah ilusi bahwa setiap kluster adalah sistem M / M / k. Misalnya, jika Anda memiliki penyeimbang pada input Anda yang mengirimkan permintaan dalam antrian ke server, ini bukan lagi M / M / k, karena M / M / k menyiratkan antrian umum dari mana server mengambil permintaan ketika mereka dirilis. Tetapi model ini cocok, misalnya, untuk kumpulan ulir dengan antrian FIFO umum. Namun, bahkan dalam kasus ini, perlu diingat bahwa aturan ini merupakan perkiraan untuk kasus ini ketika ada banyak utas. Bahkan, jika Anda memiliki lebih dari 10 utas, Anda dapat dengan aman berasumsi bahwa ada banyak utas. Nah, jangan lupa tentang distribusi eksponensial di mana-mana: tanpa mengasumsikan eksponensial dari semua distribusi, aturannya juga tidak berfungsi.

Waktu respons jaringan

Pada akhirnya, yang menarik adalah jaringan M / M / k yang terhubung setidaknya dalam sebuah rantai, karena kami membuat sistem terdistribusi. Untuk mempelajari jaringan, saya ingin memiliki konstruktor: aturan sederhana dan jelas untuk menghubungkan elemen yang diketahui ke dalam blok. Dalam teori kontrol, misalnya, ada fungsi transfer yang dimengerti dikombinasikan dengan koneksi serial atau paralel. Di sini, aliran keluaran dari sembarang simpul memiliki distribusi yang sangat rumit, dengan pengecualian M / M / k, yang, menurut teorema Burke yang terkenal , menghasilkan aliran Poisson independen. Pengecualian ini, seperti yang Anda duga, terutama digunakan.

Koneksi dua aliran Poisson adalah aliran Poisson. Pemisahan probabilistik dari aliran Poisson menjadi dua lagi memberikan dua aliran Poisson. Semua ini mengarah pada fakta bahwa semua antrian dalam sistem seolah-olah independen, dan Anda bisa mendapatkan, dalam bahasa formal, apa yang disebut solusi bentuk-produk . Yaitu, distribusi bersama panjang antrian hanyalah produk dari distribusi panjang semua antrian, dipertimbangkan secara terpisah - ini adalah bagaimana kebebasan dinyatakan dalam teori probabilitas. Kami hanya menemukan input mengalir ke semua node dan menggunakan rumus untuk setiap node secara mandiri. Ada beberapa batasan:

1. Algoritma routing probabilistik. Permintaan yang dilayani oleh node memilih berikutnya secara acak dengan probabilitas yang diketahui. Ini tidak seburuk kelihatannya, karena dimungkinkan untuk menggunakan "kelas permintaan": katakan bahwa semua permintaan Vasya datang ke server No. 1, lalu ke server No. 2 dan kemudian keluar dari jaringan, dan permintaan Petya datang ke server No. 2 , dan kemudian dengan probabilitas yang sama kunjungi server nomor 1 atau nomor 3 dan keluar. Artinya, tidak semua transisi diwajibkan untuk acak, beberapa atau bahkan semua mungkin memiliki probabilitas 100%.
2. Asumsi kemerdekaan Kleinrock. Waktu pemrosesan permintaan tidak dapat bergantung pada riwayat atau kelas permintaan, tetapi ditentukan hanya oleh server, dan ketika permintaan melewati lagi melalui server yang sama, itu dipilih secara acak setiap kali. Bahkan, tidak ada cara untuk mengatur ukuran permintaan yang akan digunakan di server yang berbeda, dan waktu layanan hanya ditentukan oleh server itu sendiri. Anda juga dapat mencoba menyiasati batasan ini. Untuk ini, rute probabilistik biasanya digunakan dan loop dibuat untuk kembali ke server yang sama dengan beberapa probabilitas - seolah-olah mereka me-restart permintaan. Menurut pendapat saya, ini adalah trik yang agak aneh, karena permintaan seperti itu kembali memasuki antrian, dan tidak dilakukan segera, tetapi untuk beberapa tugas ini tidak penting.
3. Poisson menginput lalu lintas dan waktu layanan eksponensial pada semua node.

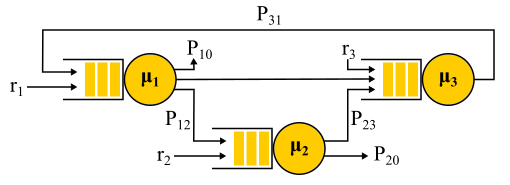
Contoh Jaringan Jackson.

Perlu dicatat bahwa di hadapan umpan balik, aliran Poisson TIDAK diperoleh, karena arus berubah menjadi saling bergantung. Pada output dari node umpan balik, aliran non-Poisson juga diperoleh, dan sebagai hasilnya, semua aliran menjadi non-Poisson. Namun, dengan cara yang mengejutkan, ternyata semua aliran non-Poisson ini berperilaku persis sama dengan aliran Poisson (oh, teori probabilitas ini) jika batasan di atas dipenuhi. Dan sekali lagi kami mendapatkan solusi bentuk-produk. Jaringan semacam itu disebut jaringan Jackson , mereka dapat memberikan umpan balik dan, karenanya, banyak kunjungan ke server mana pun. Ada jaringan lain di mana lebih banyak kebebasan diperbolehkan, tetapi sebagai hasilnya, semua pencapaian analitis yang signifikan dari teori antrian dalam kaitannya dengan jaringan melibatkan aliran Poisson pada input dan solusi bentuk-produk, yang menjadi subjek kritik terhadap teori ini dan menyebabkan pada tahun 90-an untuk. pengembangan teori-teori lain, dan studi tentang apa sebenarnya distribusi diperlukan dan bagaimana cara bekerja dengannya.

Aplikasi penting dari keseluruhan teori jaringan Jackson ini adalah pemodelan paket dalam jaringan IP dan jaringan ATM. Modelnya cukup memadai: ukuran paket tidak bervariasi banyak dan tidak tergantung pada paket itu sendiri, hanya pada lebar saluran, karena waktu layanan sesuai dengan waktu paket dikirim ke saluran. Waktu pengiriman acak, meskipun terdengar liar, sebenarnya tidak memiliki variabilitas yang sangat besar. Selain itu, ternyata bahwa dalam jaringan dengan waktu layanan deterministik, latensi tidak dapat lebih besar dari pada jaringan Jackson yang serupa, sehingga jaringan tersebut dapat digunakan dengan aman untuk memperkirakan waktu respons dari atas.

Distribusi tidak responsif

Semua hasil yang saya bicarakan berhubungan dengan distribusi eksponensial, tetapi saya juga menyebutkan bahwa distribusi nyata berbeda. Ada perasaan bahwa keseluruhan teori ini sangat tidak berguna. Ini tidak sepenuhnya benar. Ada cara untuk mengintegrasikan distribusi lain ke dalam alat matematika ini, apalagi, praktis distribusi apa pun, tetapi akan dikenakan biaya sesuatu. Dengan pengecualian beberapa kasus menarik, peluang untuk mendapatkan solusi dalam bentuk eksplisit hilang, solusi bentuk-produk hilang, dan dengan itu konstruktor: setiap masalah harus diselesaikan sepenuhnya dari awal menggunakan rantai Markov. Bagi teori, ini adalah masalah besar, tetapi dalam praktiknya itu berarti penerapan metode numerik dan memungkinkannya untuk menyelesaikan masalah yang jauh lebih kompleks dan dekat dengan kenyataan.

Metode fase

Idenya sederhana. Rantai Markov tidak memungkinkan kita untuk memiliki memori di dalam satu keadaan, oleh karena itu semua transisi harus acak dengan distribusi waktu yang eksponensial antara dua transisi. Tetapi bagaimana jika negara dibagi menjadi beberapa substate? Transisi antara substate masih harus memiliki distribusi eksponensial jika kita ingin seluruh struktur tetap menjadi rantai Markov, dan kita benar-benar ingin, karena kita tahu bagaimana menyelesaikan rantai tersebut. Sub-state sering disebut fase jika disusun secara seri, dan proses partisi disebut metode fase.

Contoh paling sederhana. Permintaan diproses dalam beberapa tahap: pertama, misalnya, kami membaca data yang diperlukan dari database, kemudian kami melakukan beberapa perhitungan, kemudian kami menulis hasilnya ke database. Misalkan ketiga tahap ini memiliki distribusi waktu eksponensial yang sama. Distribusi apa yang memiliki waktu transit dari ketiga fase secara bersamaan? Ini adalah distribusi Erlang.



Tetapi bagaimana jika Anda membuat banyak fase identik pendek? Dalam batas tersebut, kami memperoleh distribusi deterministik. Artinya, dengan membangun rantai, Anda dapat mengurangi variabilitas distribusi.

Apakah mungkin untuk meningkatkan variabilitas? Mudah Alih-alih rantai fase, kami menggunakan kategori alternatif, secara acak memilih salah satunya. Sebuah contoh Hampir semua permintaan dieksekusi dengan cepat, tetapi ada kemungkinan kecil bahwa permintaan besar akan datang, yang membutuhkan waktu lama. Distribusi semacam itu akan memiliki tingkat kegagalan yang menurun. Semakin lama kami menunggu, semakin besar kemungkinan permintaan tersebut masuk ke dalam kategori kedua.



Melanjutkan mengembangkan metode fase, ahli teori telah menemukan bahwa ada kelas distribusi yang Anda dapat mendekati dengan akurasi distribusi non-negatif sewenang-wenang! Distibusi Coxian dibangun dengan metode fase, hanya saja kita tidak diharuskan melewati semua fase, setelah setiap fase ada beberapa kemungkinan penyelesaian.



Jenis distribusi ini dapat digunakan baik untuk menghasilkan aliran input non-Poisson, dan untuk membuat waktu layanan non-eksponensial. Di sini, misalnya, adalah rantai Markov untuk sistem M / E2 / 1 dengan distribusi Erlang untuk waktu layanan. Negara ditentukan oleh sepasang angka (n, s), di mana n adalah panjang antrian, dan s adalah jumlah tahap di mana server berada: pertama atau kedua. Semua kombinasi n dan s adalah mungkin. Pesan yang masuk hanya berubah n, dan setelah selesai fase, mereka bergantian dan mengurangi panjang antrian setelah selesainya fase kedua.

Anda memiliki microbursts!

Dapatkah sistem dimuat dengan setengah kapasitasnya melambat? Sebagai subjek ujian pertama, kami menyiapkan M / G / 1. Diberikan: Aliran Poisson pada inlet dan distribusi sewenang-wenang waktu layanan. Pertimbangkan jalur permintaan tunggal melalui seluruh sistem. Permintaan masuk yang masuk secara acak melihat dalam antrian di depannya sendiri rata-rata jumlah waktu permintaan $$$\ mathbf {E} [N_Q]$ . Waktu pemrosesan rata-rata untuk masing-masing $$$\ mathbf {E} [S]$ . Dengan probabilitas sama dengan pembuangan $$$\ rho$ , ada permintaan lain di server, yang harus "dilayani" terlebih dahulu pada waktunya $$$\ mathbf {E} [S_e]$ . Kesimpulannya, kita mendapatkan total waktu tunggu dalam antrian $$$\ mathbf {E} [T_Q] = \ mathbf {E} [N_Q] \ mathbf {E} [S] + \ rho \ mathbf {E} [S_e]$ . Dengan teorema Little $$$\ mathbf {E} [N_Q] = \ lambda \ mathbf {E} [T_Q]$ ; menggabungkan, kita mendapatkan:

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ mathbf {E} [S_e]$$

Artinya, waktu tunggu dalam antrian ditentukan oleh dua faktor. Yang pertama adalah efek dari pemanfaatan server, dan yang kedua adalah waktu after-service rata-rata. Pertimbangkan faktor kedua. Permintaan tiba di beberapa titik $$$t$ , melihat bahwa setelah perawatan membutuhkan waktu $$$S_e (t)$ .



Waktu rata-rata $$$\ mathbf {E} [S_e]$ ditentukan oleh nilai rata-rata fungsi $$$S_e (t)$ , yaitu, area segitiga dibagi dengan total waktu. Jelas bahwa kita dapat membatasi diri kita pada satu segitiga "tengah" $$$\ mathbf {E} [S_e] = \ mathbf {E} [S ^ 2] / 2 \ mathbf {E} [S]$ . Ini sangat tidak terduga. Kami telah menerima bahwa waktu setelah layanan ditentukan tidak hanya oleh nilai rata-rata waktu layanan, tetapi juga oleh variabilitasnya. Penjelasannya sederhana. Probabilitas jatuh ke interval yang panjang $$$S$ lebih lanjut, ini sebenarnya sebanding dengan durasi S dari interval ini. Ini menjelaskan Paradox Waktu Tunggu yang terkenal, atau Paradox Inspeksi. Tetapi kembali ke M / G / 1. Jika Anda menggabungkan semua yang kami dapatkan dan menulis ulang menggunakan variabilitas $$$C ^ 2_S = \ mathbf {E} [S] / \ mathbf {E} [S] ^ 2$ dapatkan formula Pollaczek-Khinchine yang terkenal :

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ frac {\ mathbf {E} [S]} {2} (C ^ 2_S + 1)$$

Jika buktinya membuat Anda bosan, saya harap ini akan menyenangkan hasil penerapannya dalam praktik. Kami telah memeriksa data waktu layanan di RTMR. Ekor panjang hanya muncul dengan variabilitas besar, dan dalam hal ini $$$C ^ 2_S = 381$ . Anda tahu, ini lebih dari sekadar $$$C ^ 2_S = 1$ untuk distribusi eksponensial. Rata-rata, semuanya super cepat: $$$\ mathbf {E} [S] = 263.792 μs$ . Sekarang anggaplah bahwa RTMR dimodelkan oleh sistem M / G / 1, dan biarkan sistem tidak menjadi beban berat, pembuangan $$$\ rho = 0,5$ . Mengganti formula, kita dapatkan $$$\ mathbf {E} [T_Q] = 1 * (381 + 1) / 2 * 263.792 μs = 50 ms$ . Karena mikroburst, bahkan sistem yang cepat dan kurang dimanfaatkan dapat berubah menjadi rata-rata menjijikkan. Untuk 50 ms, Anda dapat pergi ke hard drive 6 kali atau, jika Anda beruntung, bahkan ke pusat data di benua lain! Omong-omong, untuk G / G / 1 ada perkiraan yang memperhitungkan variabilitas lalu lintas masuk: tampilannya persis sama, hanya saja $$$C ^ 2_S + 1$ itu adalah jumlah dari kedua varietas $$$C ^ 2_S + C ^ 2_A$ . Untuk kasus beberapa server, semuanya lebih baik, tetapi efek beberapa server hanya mempengaruhi faktor pertama. Efek dari variabilitas tetap: $$$\ mathbf {E} [T_Q] ^ {G / G / k} ≈ \ mathbf {E} [T_Q] ^ {M / M / k} (C ^ 2_S + C ^ 2_A) / 2$ .

Seperti apa bentuk microburst? Berkenaan dengan kolam ulir, ini adalah tugas yang dilayani cukup cepat sehingga tidak terlihat pada jadwal daur ulang, dan cukup lambat untuk membuat antrian di belakang mereka sendiri dan mempengaruhi waktu respons kolam. Dari sudut pandang teoretis, ini adalah pertanyaan besar dari ujung distribusi. Katakanlah Anda memiliki kumpulan 10 utas, dan Anda melihat jadwal daur ulang, dibangun di atas metrik waktu operasi dan waktu henti, yang dikumpulkan setiap 15 detik. Pertama-tama, Anda mungkin tidak memperhatikan bahwa satu utas tergantung sama sekali, atau bahwa semua 10 utas melakukan tugas besar secara bersamaan selama satu detik, dan kemudian tidak melakukan apa pun selama 14 detik. Resolusi 15 detik tidak memungkinkan untuk melihat lompatan pemanfaatan hingga 100% dan kembali ke 0%, dan waktu responsnya terganggu. , , 15 6 , .



, ( ) .

, RTMR SelfPing, ( 10 ), — . , 10 15 . , . , , 10 , , — . self-ping- CPU. , : , , . : , , . : . , 15- , — .

, , SelfPing , ? ? , LWTrace. , . -100 . . : ; — , , ; perf , , .

« », . , , . FIFO-. , , latency ( SPT SRPT). — . , , , . , « », .

, - product-form solution . M/ Cox /1/ PS . , (Coxian distribution) (Processor Sharing), , , . ? , . , , (. ) , , M/ M /1/ FIFO , , .

! , , , ! insensitivity property. , , , , . — M/M/∞. , . , product-form solution — BCMP .

. , (, ), , , ó . . Solusi $$$\mathbf{E}[T] = 1/3 \mathbf{E}[T_1] + 2/3 \mathbf{E}[T_2]$ . $$$\mathbf{E}[T_i] = 1/(\mu_i - \lambda_i)$ M/M/1/FCFS $$$\mathbf{E}[T] = 1/3 * 1/(3 - 3 * 1/3) + 2/3 * 1/(4 - 3*2/3) = 0.5$ .

, , . , .

1. , , , computer science, . Performance Modeling and Design of Computer Systems: Queueing Theory in Action (2013). - , . ó — .
2. , , , , Robert B. Cooper. , .