Pengambilan sampel tangki (ind. "Pengambilan sampel reservoir") adalah algoritma yang sederhana dan efisien untuk pengambilan sampel secara acak sejumlah elemen dari vektor yang ada dengan ukuran besar dan / atau tidak diketahui. Saya tidak menemukan artikel tentang algoritma ini di Habré dan karena itu memutuskan untuk menulis sendiri.
Jadi, apa yang kita bicarakan. Memilih satu elemen acak dari vektor adalah tugas dasar:
Tugas "mengembalikan elemen acak K dari vektor ukuran N" sudah lebih rumit. Di sini Anda sudah dapat membuat kesalahan - misalnya, mengambil elemen K pertama (ini melanggar persyaratan keacakan) atau mengambil setiap elemen dengan probabilitas K / N (ini melanggar persyaratan untuk mengambil elemen K persis). Selain itu, dimungkinkan untuk menerapkan solusi yang benar secara formal, tetapi sangat tidak efektif "secara acak mencampur semua elemen dan mengambil K terlebih dahulu." Dan semuanya menjadi lebih menarik jika kita menambahkan syarat bahwa N adalah angka yang sangat besar (kita tidak memiliki cukup memori untuk menyimpan semua elemen N) dan / atau tidak diketahui sebelumnya. Misalnya, bayangkan bahwa kita memiliki semacam layanan eksternal yang mengirimkan elemen satu per satu. Kami tidak tahu berapa banyak dari mereka akan datang semua, dan kami tidak bisa menyimpan semuanya, tetapi kami ingin memiliki satu set elemen K yang dipilih secara acak dari yang diterima pada waktu tertentu.
Algoritma sampling reservoir memungkinkan kita untuk menyelesaikan masalah ini dalam langkah O (N) dan memori O (K). Dalam hal ini, tidak perlu mengetahui N terlebih dahulu, dan kondisi pengambilan sampel acak elemen K akan diamati dengan jelas.
Mari kita mulai dengan tugas yang disederhanakan.
Misalkan K = 1, mis. kita hanya perlu memilih satu elemen dari semua elemen yang masuk - tetapi agar setiap elemen yang masuk memiliki probabilitas yang sama untuk dipilih. Algoritme menyarankan sendiri:
Langkah 1 : Alokasikan memori ke tepat satu elemen. Kami menyimpan di dalamnya elemen pertama tiba.

Sejauh ini, semuanya OK - hanya ada satu elemen yang datang kepada kita, dengan probabilitas 100% (saat ini) harus dipilih - itu.
Langkah 2 : Elemen masuk kedua ditulis ulang dengan probabilitas 1/2 sebagai yang dipilih.

Di sini juga, semuanya baik-baik saja: sejauh ini, hanya dua elemen yang datang kepada kita. Yang pertama tetap dipilih dengan probabilitas 1/2, yang kedua ditulis ulang dengan probabilitas 1/2.
Langkah 3 : Elemen masuk ketiga dengan probabilitas 1/3 ditulis ulang sebagai yang dipilih.
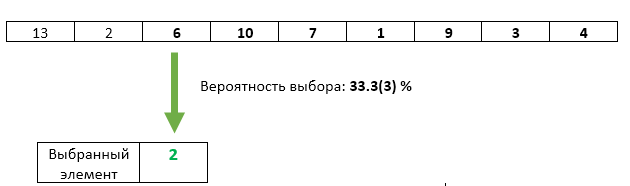
Semuanya baik-baik saja dengan elemen ketiga - peluangnya untuk dipilih tepat 1/3. Tetapi apakah kita dengan cara apa pun melanggar peluang yang sama dari elemen sebelumnya? Tidak. Probabilitas bahwa item yang dipilih tidak akan ditimpa pada langkah ini adalah 1 - 1/3 = 2/3. Dan karena pada langkah 2 kami menjamin peluang yang sama untuk setiap elemen yang akan dipilih, maka setelah langkah 3 masing-masing dapat dipilih dengan peluang 2/3 * 1/2 = 1/3. Peluang yang sama persis dengan elemen ketiga.
Langkah N : Dengan probabilitas 1 / N, elemen nomor N ditulis ulang sebagai yang dipilih. Setiap item sebelumnya yang tiba memiliki peluang 1 / N yang sama untuk tetap dipilih.
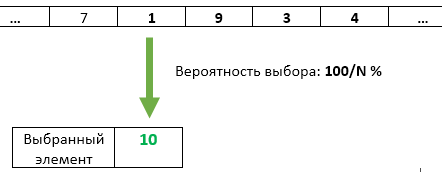
Tapi itu tugas yang disederhanakan, dengan K = 1.
Bagaimana perubahan algoritma untuk K> 1?
Langkah 1 : Kami mengalokasikan memori pada elemen K. Kami menulis di dalamnya elemen K pertama tiba.

Satu-satunya cara untuk mengambil elemen K dari elemen yang tiba adalah mengambil semuanya :)
Langkah N : (untuk setiap N> K): menghasilkan angka acak X dari 1 hingga N. Jika X> K maka kita membuang elemen ini dan melanjutkan ke yang berikutnya. Jika X <= K, maka tulis ulang elemen dengan angka X. Karena nilai X akan seragam secara acak dalam kisaran dari 1 hingga N, di bawah kondisi X <= K akan secara acak seragam di kisaran dari 1 hingga K. Dengan demikian, kami memastikan keseragaman. pemilihan item yang dapat ditulis ulang.

Seperti yang Anda lihat, setiap elemen berikutnya yang datang memiliki kesempatan yang semakin sedikit untuk dipilih. Namun demikian, itu akan selalu tepat K / N (seperti untuk masing-masing elemen sebelumnya tiba).
Keuntungan dari algoritma ini adalah kita dapat berhenti kapan saja, menunjukkan kepada pengguna vektor K saat ini - dan ini akan menjadi vektor elemen acak yang dipilih secara jujur dari urutan elemen yang tiba. Mungkin ini cocok untuk pengguna, atau mungkin dia ingin terus memproses nilai yang masuk - kita dapat melakukan ini kapan saja. Dalam hal ini, seperti yang disebutkan di awal, kami tidak pernah menggunakan lebih dari memori O (K).
Oh ya, saya benar-benar lupa, fungsi
std :: sample , yang melakukan persis seperti yang dijelaskan di atas, akhirnya dimasukkan dalam pustaka C ++ 17 standar. Standar tidak mewajibkannya untuk menggunakan hanya pengambilan sampel reservoir, tetapi mewajibkannya untuk bekerja dalam langkah-langkah O (N) - yah, tidak mungkin bahwa pengembang penerapannya di perpustakaan standar akan memilih beberapa algoritma yang menggunakan lebih dari memori O (K) (dan lebih sedikit akan gagal juga - hasilnya perlu disimpan di suatu tempat).
Materi Terkait