Sortir "Menara Hanoi"

^{Menara Hanoi}
Hanya orang malas yang tidak menulis tentang permainan Eduard Luc yang terkenal di Habré. Tampaknya semua penutup sudah robek dan sesuatu yang lain tentang algoritma tidak lagi mungkin untuk ditambahkan. Tapi tidak, topik ini memiliki sumber tersembunyi. Hari ini, khususnya, kami akan mengulang algoritma untuk memecahkan teka-teki ini menjadi semacam lengkap. (Kenapa? Hanya untuk bersenang-senang. Jumat dimungkinkan.)

Posting ini didedikasikan untuk mengenang guru pemrograman sejati Andrei Mrrl Astrelin, yang pernah menjelaskan algoritma ini kepada saya secara sederhana dan cerdas. Kode pseudo di bawah adalah teks kepengarangannya.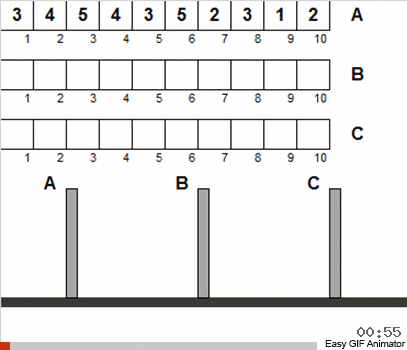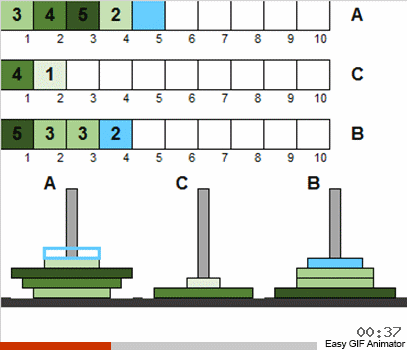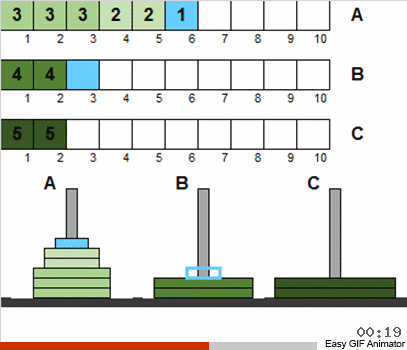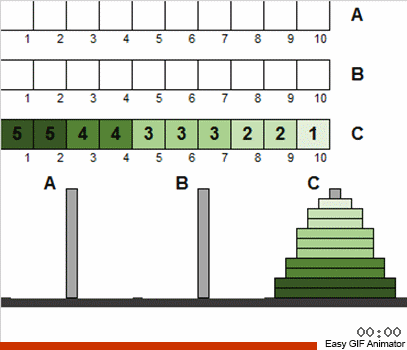


Dalam teka-teki klasik, cakram pada tiang pertama awalnya dipesan. Tapi kami akan membiarkan mereka digantung dalam urutan apa pun.

Selain itu, ukuran disk diasumsikan unik. Kami tidak akan berpegang teguh pada pembatasan ini dan mengizinkan pengulangan.

Jika Anda hanya mengizinkan dua kebebasan ini, maka kondisi awal teka-teki dapat diartikan sebagai array (disk adalah angka), dan tugas bermuara pada kenyataan bahwa array ini perlu disortir.

Kondisi yang tersisa kami (hampir) tidak berubah:

• Kami memiliki dua kutub bantu (sepasang array kosong).
• Kami dapat mentransfer disk satu per satu.
• Hanya menempatkan yang lebih kecil ke yang lebih besar (karena kami telah mengizinkan ukuran disk yang sama, kami juga dapat menempatkan disk yang dipindahkan di atas yang lain dengan ukuran yang sama).
• Kami memiliki hak untuk membandingkan disk portabel dengan hanya disk teratas (yaitu, semua 3 array adalah tumpukan).

Tugas kami: untuk mengambil algoritma puzzle rekursif klasik ...

def hanoi(n, source, helper, target): if n > 0: hanoi(n - 1, source, target, helper) if source: target.append(source.pop()) hanoi(n - 1, helper, source, target) 

... dan mengubahnya menjadi penyortiran!

Bahkan, dari fakta bahwa kami mengizinkan gangguan awal dan pengulangan untuk ukuran disk, tidak ada yang berubah secara mendasar dari ini. Pada umumnya, masalah diselesaikan dengan cara rekursif klasik yang sama. Hal yang paling penting untuk dipahami adalah bahwa semua gerakan disk dibagi menjadi beberapa tahap, yang masing-masing adalah miniatur klasik Hanoi.

Artinya, pada setiap tahap kami tidak mempertimbangkan semua disk yang tersedia, tetapi hanya totalitas yang memenuhi kondisi lama. Setelah mengurutkan set kecil ini dengan klasik, kami akan membawa keadaan umum sistem lebih dekat ke puzzle klasik. Kemudian kami kembali mengambil set disk yang sesuai dengan klasik dan menerapkan algoritma yang terkenal lagi. Dan set ini akan lebih besar dari pada langkah sebelumnya! Jadi kami ulangi sampai semua disk di semua kutub tiba-tiba menjadi berbeda dari keadaan klasik.

Sistem yang awalnya rusak (oleh fakta bahwa disk tidak dipesan pada input) adalah penyembuhan sendiri dengan setiap iterasi.

Adapun resolusi pengulangan, ini tidak masalah sama sekali. Karena disk identik berturut-turut kami hanya bergerak sebagai satu disk.

Algoritma

Kami menyebut kolom A , B , C ( A pada awalnya adalah kosong).

Kami memperkenalkan operasi:

A -> C () - menggeser satu disk dari A ke C.
top (A) , top (C) - ukuran disk bagian atas A atau C. Jika kolom kosong, maka ukuran ini = MaxInt .
B -> C ( K ) - bergeser dari B ke C semua disk yang ukurannya kurang dari K (kita bisa melakukan ini jika disk A dan C atas tidak kurang dari K ).
swap () - mengatur ulang kolom B dan C (atau mengganti nama mereka - kami tidak peduli di mana disk berada).
while ( A ) - loop sampai A kosong.

Kemudian algoritma berikut ini berfungsi:

 //      A    ""  while(A) { K = top(A); //-""    while(top(C) < K){ B->C(top(C)); swap(); } A->C(); } // .  -  "" while(C) { B->C(top(C)); swap(); } 

© Tuan

Kesulitan

Dalam kasus terburuk, pengurutan cenderung kompleksitas waktu untuk algoritma klasik, yang, meskipun sederhana dan elegan, pada saat yang sama secara maksimal tidak efisien. Adapun yang terbaik dan rata-rata, saya merasa sulit untuk berasumsi.

Adapun memori, kita dapat mengatakan bahwa jika rekursi digunakan, maka biayanya akan sesuai.

Implementasi

Saya belum menulis versi saya sendiri dengan Python (saya akan melakukannya nanti). Namun, di bagian "Tautan" di bawah ini, saya memposting beberapa tautan tempat Anda dapat melihat implementasi dalam berbagai bahasa. Opsi yang sangat menarik di Jawa. Penulis tidak mengambil sebagai dasar metode rekursif terkenal untuk memecahkan teka-teki, tetapi membangun pohon jalur terpendek. Agaknya, ini adalah solusi paling efektif jika Anda menulis penyortiran dengan gaya "Menara Hanoi."

Karakteristik Algoritma

Referensi

Menara Hanoi

Implementasi: C , Java vs C ++ vs Python , Python .

Artikel Seri:

• Aplikasi Excel AlgoLab.xlsm
• Pertukaran macam
• Urutan Penyisipan
  • Sortir Pustakawan
  • Sortir Solitaire
  • Sortir "Menara Hanoi"
  • Penyortiran meja muda
  • Balikkan Sortir
  • Masukkan Sortir Perbandingan
• Sortir berdasarkan pilihan
• Gabungkan Urusan
• Urutkan berdasarkan distribusi
• Sortasi Hibrid

Di aplikasi AlgoLab, pengurutan ini sekarang tersedia. Meskipun termasuk dalam jenis kelas oleh sisipan, karena pemborosan algoritma, ia ditempatkan di bagian "Jenis lain". Ada juga batasan - angka-angka dalam array yang diurutkan hanya dari 1 hingga 5 (karena sulitnya rendering disk). Nomor lain masih akan diganti oleh ini.

Ada juga batasan ukuran array - tidak lebih dari 20 elemen. Ini dilakukan murni untuk kepentingan Anda sendiri - jika Anda mengambil array yang terlalu besar, mungkin Anda harus mengurutkannya hingga usia yang sangat tua.

Artikel ini ditulis dengan dukungan EDISON Software, sebuah perusahaan yang secara profesional mengembangkan pencahayaan kota pintar dan memelihara situs-situs Python.