Teori kebahagiaan. Kecelakaan tidak disengaja?

Saya terus berkenalan dengan para pembaca Habr dengan bab-bab dari bukunya "Theory of Happiness" dengan subtitle "Yayasan Matematika dari Hukum Makna." Ini belum diterbitkan buku sains populer, sangat informal menceritakan tentang bagaimana matematika memungkinkan Anda untuk melihat dunia dan kehidupan orang-orang dengan tingkat kesadaran yang baru. Ini untuk mereka yang tertarik pada sains dan bagi mereka yang tertarik pada kehidupan. Dan karena kehidupan kita kompleks dan, pada umumnya, tidak dapat diprediksi, penekanan dalam buku ini terutama pada teori probabilitas dan statistik matematika. Di sini teorema tidak terbukti dan dasar-dasar sains tidak diberikan, ini sama sekali bukan buku teks, tetapi apa yang disebut ilmu rekreasi. Tetapi justru pendekatan yang hampir menyenangkan yang memungkinkan kami untuk mengembangkan intuisi, mencerahkan kuliah untuk siswa dengan contoh-contoh nyata dan, akhirnya, menjelaskan kepada non-matematikawan dan anak-anak kami bahwa kami menemukan hal-hal menarik dalam ilmu kering kami.



Dalam bab ini, kita membahas penerbangan koin yang telah ditentukan, peta topografi, bencana matematika, dan sifat keacakan. Dan di sepanjang jalan, mari kita lihat bagian matematika seperti teori ukuran dan teori kekacauan dinamis.

Percakapan tentang hukum kekejaman, sebagai sumber kekacauan sehari-hari, sering dimulai dengan hukum sandwich yang terkenal . Ini hanya dirumuskan, mudah diverifikasi dan dikenal luas:

Sandwich selalu menjatuhkan mentega ke bawah.

Jelas bahwa kata "selalu" di sini berlebihan. Sangat mudah untuk membayangkan kondisi di mana sandwich akan jatuh, membuat sisi yang berminyak tetap utuh. Apa yang dipahami orang oleh hukum ini? Kemungkinan besar, sandwich sering kali jatuh dengan mentega agar terlihat. Tetapi apakah hasil yang tidak menguntungkan dari jatuh lebih mungkin daripada yang menguntungkan? Sandwich berbeda, mereka jatuh dalam keadaan yang berbeda, dari ketinggian yang berbeda ... Ada begitu banyak parameter yang mungkin tidak ada gunanya berbicara tentang pola dalam tugas seperti itu. Apa pun bisa terjadi. Kebetulan minyak itu jatuh ke dalam minyak, lalu menjadi menghina, kita mengingat hukum dan mengingatnya. Dan jika sandwich tidak menarik - dengan minyak naik, atau jika ternyata tanpa minyak sama sekali, tidak ada yang perlu dibicarakan - jelas bahwa hukumnya adalah komik! Pada akhirnya, sandwich seperti koin, yang digunakan matematikawan untuk mendapatkan variabel acak dengan dua nilai yang mungkin: "elang" dan "ekor". Jika koin itu "jujur", maka sama sekali tidak masalah sisi mana yang akan jatuh, dan kami mengatakan bahwa probabilitas elang dan ekornya jatuh adalah sama dan setara. $$$1/2$ . Secara teori, sandwich harus sama. Kami akan kembali kepada mereka di bab berikutnya, tetapi untuk sekarang mari kita lihat sistem probabilistik sederhana yang paling mungkin - koin.

Koin dalam eksperimen probabilitas-teoretis dilemparkan dengan cara magis khusus, sehingga pilihan posisi awal, kecepatan awal, dan kecepatan putaran selama lemparan tidak mempengaruhi probabilitas hasil tertentu. Tetapi jelas bahwa ini tidak mungkin! Koin adalah sistem mekanis dan mematuhi hukum mekanika, tetapi koin tidak mengandung variabel acak. Masa depan dalam hukum gerak tubuh yang sederhana seperti koin secara unik ditentukan oleh kondisi tubuh sebelumnya. Jika robot membalik koin, atau iblis Laplace adalah makhluk mitos yang memiliki informasi lengkap tentang koordinat dan kecepatan sistem mekanis apa pun, maka hasil yang sama akan diperoleh dengan data awal yang konstan. Kita, tentu saja, bukan robot atau setan, tetapi apakah orang benar-benar melempar koin dengan ceroboh dan tidak dapat diprediksi sehingga hukum mekanika dapat menyebabkan kecelakaan?

Dan dari mana, secara umum, keacakan berasal dari dunia yang dijelaskan oleh hukum mekanika? Dari mana asal acak? Apa perbedaan antara sistem yang benar-benar kacau atau stokastik, yang pada dasarnya tidak dapat diprediksi, dan sistem yang sulit untuk menebak perilakunya, tetapi dapat dihitung?

Masalah koin dipertimbangkan pada tahun 1986 oleh Joseph Keller. Kami memberikan penjelasan sederhana untuk terjadinya ketidakpastian dalam proses ini, berdasarkan alasan dari artikel Keller. Di sisi mana koin akan jatuh tergantung pada waktu penerbangannya. $$$t$ dan dari kecepatan sudut $$$\ omega$ . Jika Anda mengukur kecepatan sudut dalam putaran per satuan waktu, maka jumlah putaran yang dibuat oleh koin dinyatakan sangat sederhana. $$$n = t \ omega$ . Ketergantungan ini menetapkan garis jumlah revolusi yang sama dalam koordinat $$$(t, \ omega)$ , dan mereka, pada gilirannya, membatasi area yang sesuai dengan jumlah revolusi genap dan ganjil.

Diagram menunjukkan paritas jumlah revolusi yang dilakukan oleh koin dalam penerbangan. Persegi panjang menunjukkan area di mana proses peramalan nasib pada koin paling sering terjadi.

Dalam diagram seperti itu, dimungkinkan untuk menunjukkan apa hasil dari flip koin, dipelintir dengan jumlah putaran yang diketahui per detik, dan ditangkap setelah waktu flip yang diketahui. Jika kita jatuh ke strip putih, maka sisi yang sama akan drop out yang berada di atas ketika melemparkan, jika berwarna oranye - sebaliknya. Garis dengan kecepatan yang sama adalah hiperbola dan dapat dilihat bahwa saat kecepatan meningkat, pergantian area menjadi semakin sering, dan area itu sendiri menjadi lebih tipis. Tangan manusia tidak sempurna dan sebaran kecil nilai awal mencakup banyak bidang sekaligus, sehingga hasilnya tidak dapat diprediksi. Dalam rentang tangan (persegi panjang dalam diagram), offset cukup $$$5 \%$ untuk melompat dari garis putih ke oranye. Pertanyaannya tetap: bagaimana "kejujuran" dari koin mekanik nyata mengikuti dari konstruksi ini? Bagaimana cara mendapatkan kemungkinan hilangnya elang atau ekor dari diagram yang dihasilkan?

Segera ambil tindakan!

Kami akan terjun sedikit ke matematika yang tidak diajarkan di sekolah untuk lebih memahami apa yang sedang kita diskusikan. Kami mengatakan dalam pengantar bahwa matematikawan tidak mempelajari angka atau bentuk geometris, seperti yang terlihat setelah mempelajari kursus sekolah. Mereka bekerja dengan struktur matematika (aljabar abstrak, setengah cincin, bidang, monoids, ruang topologi dan hal-hal abstrak lainnya), menggambarkan mereka, seolah-olah, sama sekali tidak terikat untuk berlatih, mendefinisikan mereka, mempelajari sifat-sifat mereka, membuktikan teorema. Dan kemudian mereka mengasah keterampilan mereka dalam menemukan struktur seperti itu di berbagai bidang pengetahuan, membuat terobosan yang sangat berguna, termasuk di bidang yang diterapkan murni. Kami sekarang akan menyentuh sedikit matematika seperti itu dan mempertimbangkan bagaimana dasar teori probabilitas dibangun berdasarkan konsep ukuran yang sangat abstrak.

Kami menggambarkan mekanisme koin dan memperoleh area yang menggambarkan serangkaian solusi dengan properti tertentu. Area adalah angka datar, bagaimana cara beralih dari mereka ke probabilitas dengan benar? Kita perlu mengukur daerah kita dan kita secara alami datang ke daerah mereka. Area - adalah ukuran sosok datar. Ini adalah istilah matematika yang tepat untuk fungsi yang mengaitkan set dengan nilai numerik non-negatif tertentu. Contoh ukuran adalah jumlah dalam himpunan enumerasi (jumlah apel dalam tas, misalnya), serta panjang , luas , volume gambar .

Ada seluruh bagian dalam matematika yang disebut teori ukuran . Teori ini lahir pada pergantian abad XIX - XX (Emil Borel dan Henri Lebesgue berdiri pada asalnya) dan terbuka untuk matematikawan peluang yang cukup untuk menganalisis objek yang sangat kompleks: cantor dan set fraktal. Ini membentuk dasar analisis fungsional dan teori probabilitas modern, fondasi yang diletakkan oleh ahli matematika Rusia yang luar biasa Andrei Kolmogorov. Definisi probabilitas, sebagai ukuran, memungkinkan Anda untuk melihat semua sifat dasar probabilitas untuk set diskrit dan kontinu.

Meskipun buku kami bukan buku teks, ada baiknya berhenti sedikit untuk melihat konsep thorium probabilitas dari pandangan mata burung dan merasakan cita rasa matematika. Untuk memulainya, kami mencantumkan properti utama dari setiap tindakan. Agar dapat membayangkannya dengan lebih baik, Anda dapat menggunakan kata "kuantitas" atau "panjang" atau "area" alih-alih kata "ukur".

1. Ukuran set kosong adalah nol.
2. Ukuran seluruh himpunan terukur terbatas hingga langkah-langkah terbatas.
3. Ukuran subset tidak melebihi ukuran set
4. Ukuran penyatuan dua set arbitrer sama dengan jumlah ukuran set-set ini dikurangi ukuran persimpangan mereka (aditivitas).
5. Ukuran melengkapi subset sama dengan perbedaan antara ukuran seluruh set dan ukuran subset.

Bisakah fungsi numerik non-negatif menjadi tolok ukur? Tidak semuanya. Misalnya, usia memberi seseorang angka yang sepenuhnya spesifik. Tetapi usia dua orang tidak dapat didefinisikan sebagai jumlah dari usia mereka. Dan kecepatan lari bukanlah ukuran - dua orang berlari tidak dua kali lebih cepat. Tetapi momentum (momentum) atau energi sudah memiliki sifat suatu ukuran. Berat, jumlah uang, jumlah pengetahuan, volume tangisan, meskipun tidak selalu mudah diukur, juga bisa berfungsi sebagai ukuran bagi banyak orang.

Pada tingkat intuitif, hampir semua orang akrab dengan konsep probabilitas sekarang. Diperkirakan oleh para ilmuwan politik dan wartawan di acara bincang-bincang, dibahas berbicara tentang pemanasan global atau hujan esok hari, bercanda tentang hal itu diceritakan: Bagaimana kemungkinan bertemu seekor dinosaurus di Tver? - Satu detik: rapat atau tidak. Dalam matematika modern, konsep probabilitas didefinisikan sebagai ukuran pada set khusus yang disebut ruang probabilitas . Ini mencakup peristiwa elementer dan kombinasinya yang diperoleh dengan menggunakan operasi penyatuan, persimpangan dan pengecualian. Contoh acara dasar: "kehilangan tiga kali lipat saat melempar tulang." Contoh acara yang tidak elementer: "hilangnya bilangan genap apa pun kecuali dua." Jadi, kami mencantumkan properti probabilitas:

1. Probabilitas suatu peristiwa yang mustahil adalah nol.
2. Probabilitas untuk seluruh ruang probabilitas sama dengan kesatuan.
3. Jika satu peristiwa juga memerlukan yang lain, maka probabilitas yang kedua tidak melebihi probabilitas yang pertama. Di sini, relasi "memerlukan" untuk acara adalah setara dengan "adalah himpunan bagian" untuk set dan tidak berarti "adalah penyebab".
4. Probabilitas terjadinya setidaknya satu dari dua peristiwa sewenang-wenang adalah sama dengan jumlah probabilitas masing-masing peristiwa ini, dikurangi probabilitas bahwa peristiwa tersebut akan terjadi secara bersamaan.
5. Probabilitas suatu peristiwa tidak terjadi adalah satu dikurangi probabilitas suatu peristiwa terjadi.

Lihatlah lebih dekat pada properti ukuran dan probabilitas dan Anda akan melihat bahwa kita berbicara tentang properti yang sama.

Tidak semua sifat probabilitas muncul dari definisi sebagai ukuran: konsep independensi peristiwa dan metode penghitungan probabilitas dua atau lebih peristiwa independen secara bersamaan karena produk dari probabilitas diperkenalkan melalui probabilitas kondisional , tetapi konsep ini konsisten dengan definisi Kolmogorov.

Variabel acak diskrit sesuai dengan himpunan yang dapat dihitung terbatas, di dalamnya, ukuran alami adalah jumlah biasa dari jumlah elemen. Dengan demikian, probabilitas dalam ruang probabilistik diskrit adalah perhitungan kombinasi opsi yang akrab bagi setiap siswa. Untuk variabel acak kontinu, probabilitas, sebagai ukuran, lebih mirip panjang atau luas, dan di sini kita berbicara tentang kepadatan probabilitas .

Analogi probabilitas dengan ukuran tidak berakhir di sana. Berapa nilai rata - rata ? Ini adalah analog dari posisi pusat massa suatu gambar yang terdiri dari titik massa atau padatan dengan kerapatan yang diketahui. Dan jumlah ini dihitung dengan cara yang sama. Dan bagaimana dispersi variabel acak di sekitar rata-rata ditandai: varians ? Persis seperti momen inersia yang menjadi ciri distribusi massa di sekitar pusat massa. Dan lagi, rumus untuk menghitung varians untuk sampel atau distribusi bertepatan dengan rumus untuk momen inersia seperangkat benda atau benda padat bentuk licik.

Ngomong-ngomong, jika kita mengganti definisi dan sifat probabilitas jumlah dengan “maksimum” dan produk dengan “minimum”, maka kita dapat membangun teori alternatif, itu disebut teori kemungkinan . Beginilah cara kerja matematika. Kita mulai dengan penalaran abstrak: angka membentuk aljabar dengan operasi penjumlahan dan perkalian, tetapi pada interval angka terbatas, Anda dapat membangun aljabar serupa dengan operasi minimum dan maksimum. Kami membangun konsep ukuran pada aljabar baru dan menemukan bahwa itu membuka pandangan dunia yang baru! Berbeda dengan teori probabilitas, dalam teori semacam itu dua ukuran terkoordinasi dapat dibangun - kemungkinan dan kebutuhan , dan, tidak seperti probabilitas, mereka dalam perjanjian yang baik dengan serikat dan operasi persimpangan. Arahan ini dibuat oleh Lotfi Zadeh Amerika, asal Azerbaijan, berfungsi sebagai dasar untuk logika fuzzy dan digunakan dalam pengenalan pola otomatis dan sistem pengambilan keputusan.

Luar biasa, tetapi benar!

Properti langkah-langkah pertama tampaknya sepele, tetapi menarik dalam asimetrisnya. Jika ukuran subset adalah nol, ini tidak berarti kosong! Misalnya, garis adalah himpunan bagian dari titik-titik pada pesawat, tetapi luasnya (ukur) adalah nol. Ada contoh yang lebih eksotis - Cantor dan set fraktal, memiliki struktur yang kompleks, mengandung jumlah poin yang tak terbatas, secara visual "menempati" area atau volume tertentu, tetapi tetap memiliki ukuran nol.

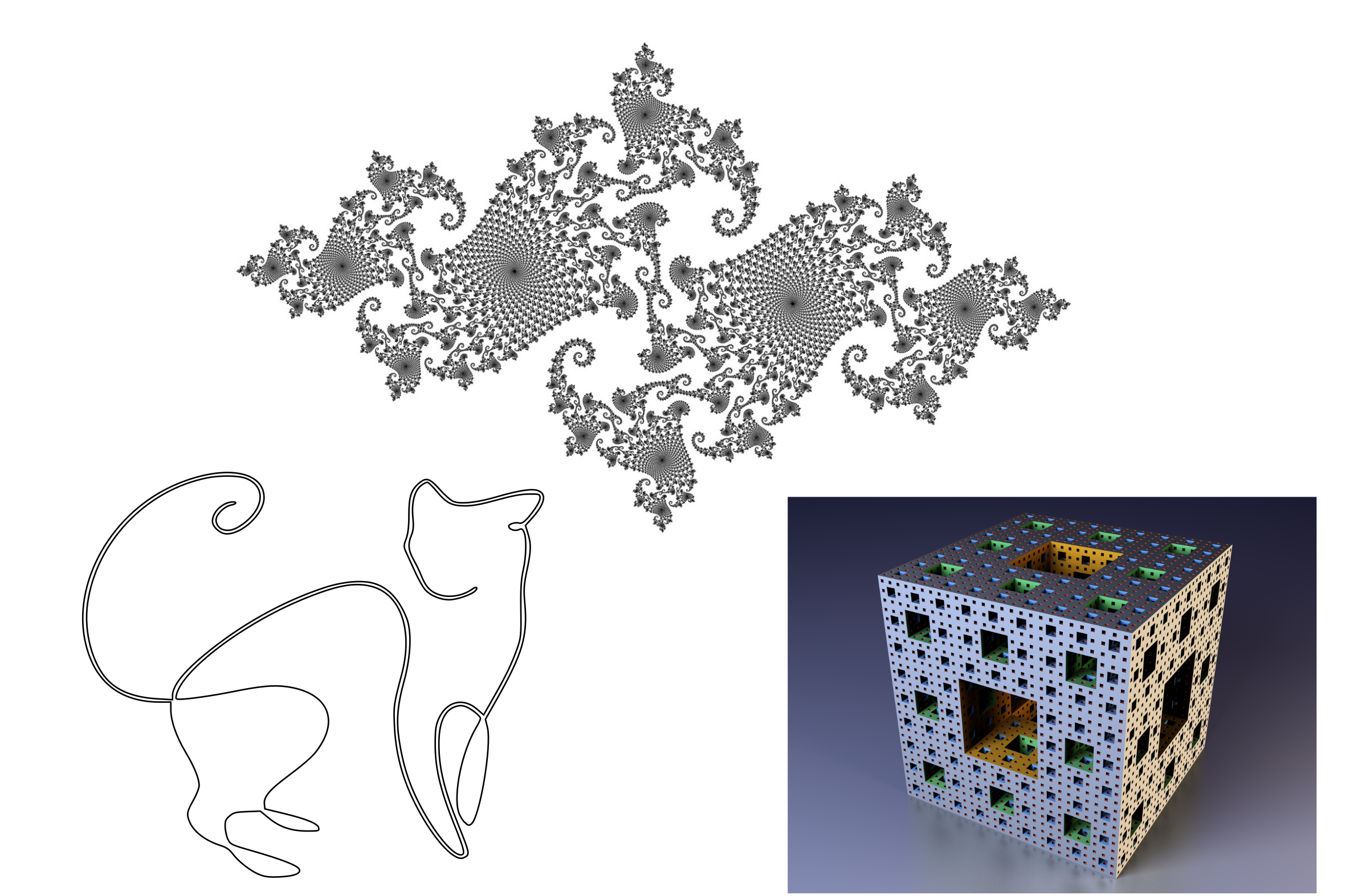Beberapa objek tanpa ukuran: garis di pesawat, set Julia sporadis, spons fraksi Menger.

Saat mempersiapkan ilustrasi ini, saya menemukan gambar yang indah dari rangkaian Julia yang terputus pada latar transparan dengan resolusi tinggi. Setelah memasukkannya ke editor vektor, saya menemukan kesulitan yang lucu - sangat sulit untuk masuk ke gambar ini dengan mouse untuk memilihnya. Sangat "longgar" sehingga kemungkinan untuk masuk ke piksel yang terisi terasa kurang dari masuk ke latar belakang transparan. Dalam ruang probabilitas, himpunan bagian dari ukuran nol mungkin juga ada, tetapi ini tidak berarti bahwa peristiwa dari himpunan bagian ini tidak mungkin. Dari upaya keempat hingga kelima, saya masih dapat memilih gambar, karena piksel memiliki ukuran yang terbatas. Tetapi apa yang akan terjadi jika saya siap dengan satu set Julia nyata tidak koheren dengan resolusi tak terbatas?

Bayangkan Anda menggunakan generator nomor acak perangkat lunak yang menghasilkan bilangan real arbitrer $$$0$ sebelumnya $$$1$ . Berapakah probabilitas suatu angka jatuh? $$$0$ ? dan angka $$$1/2$ atau $$$e / \ pi$ ? Dalam semua kasus ini, jawabannya adalah - nol! Sebaliknya, angka positif terkecil yang tersedia untuk komputer, yang disebut mesin epsilon, karena komputer beroperasi dengan jumlah desimal yang terbatas. Tunggu, katamu, dalam arti apa nol? Angka yang sama bukan tidak mungkin. Mari kita melakukan percobaan, sebagai hasilnya kita mendapatkan beberapa angka tertentu, dan ketika kita mendapatkannya, maka "dengan konstruksi" probabilitas penampilannya tidak boleh nol. Itu benar, tetapi berapa lama saya harus menunggu sampai tepat 0 keluar? Hampir tanpa akhir! Faktanya adalah bahwa angka tunggal, seperti titik pada suatu segmen, memiliki ukuran nol dan probabilitas nol jujur. Hanya ukuran segmen kontinu, bahkan yang sangat kecil, adalah nol. Jadi kita tidak berbicara tentang probabilitas, tetapi tentang kepadatan probabilitas, yang, ketika dikalikan dengan ukuran terbatas dari subset dalam ruang probabilitas, akan memberikan nilai hingga - probabilitas jatuh ke dalam subset ini. Omong-omong, berubah menjadi penghasil bilangan acak ideal kami dengan akurasi tak terbatas, kemungkinan mendapatkan bilangan rasional (bukan beton, tetapi ada) dengan itu juga akan menjadi nol. Bukti bahwa bilangan rasional membentuk subset padat dari ukuran nol himpunan bilangan real membuat kebisingan pada akhir abad ke-19.

Jika seseorang dengan sabar melakukan seribu percobaan dengan koin dan dengan senang hati memberi tahu Anda bahwa ia mendapatkan "elang" sebanyak yang ia lakukan "berekor", Anda dapat dengan aman mengungkapkan keraguan atau memberi selamat kepadanya atas keberuntungan yang langka. Meskipun melempar koin dan proses acak terpisah, ketika statistik menumpuk, kekuatan ruang probabilitas akan meningkat dan ukuran acara: "jumlah" elang "bertepatan dengan jumlah" ekor "" akan berkurang. Dapat ditunjukkan, menggunakan rumus Stirling, bahwa probabilitas peristiwa "paling mungkin" ini cenderung nol dengan peningkatan jumlah tes sebagai $$$1 / \ sqrt {\ pi n}$ . Untuk seratus pemain, ini sedikit lebih dari lima persen, untuk sepuluh ribu - hanya setengah persen. Dalam kasus seperti itu, ahli matematika mengatakan: hampir pasti jumlah "elang" tidak akan sama dengan jumlah "ekor" . Tidak peduli betapa aneh kedengarannya, tetapi "hampir pasti" adalah istilah matematika yang tepat, yang berarti bahwa acara tersebut merupakan pelengkap bagi subset ruang probabilitas dari ukuran nol. Kita akan kembali ke pertimbangan ini dalam salah satu bab berikut ketika kita bertanya pada diri sendiri: seberapa banyak dari kita masing-masing dapat menganggap diri kita normal.

Memeriksa kejujuran koin asli

Mari kita kembali ke koin dan kejujurannya. Definisi Kolmogorov tentang probabilitas mendamaikan definisi frekuensinya (sebagai frekuensi relatif dari peristiwa yang terjadi) dan geometris (sebagai sebagian kecil dari "volume" suatu peristiwa dalam "volume" total kemungkinan). Dengan demikian, fraksi luas garis-garis putih dalam diagram yang dihitung untuk koin berputar mencerminkan kemungkinan jatuh dari sisi yang sama dengan yang kita lemparkan.

Tapi masalahnya! Luas setiap strip dalam diagram kami tidak terbatas (jika kami mempertimbangkan seluruh kuartal bidang koordinat). Namun, aditivitas ukuran akan memungkinkan kita untuk secara akurat menunjukkan bahwa ini tidak mencegah area yang diarsir dan putih menjadi sama. Dalam bentuk eksplisit, persamaan untuk kurva kami memiliki bentuk$$$\omega = n/t$ . Jika area di bawah kurva $$ω = 1 / t sama$\omega = 1/t$$$S , kemudian karena sifat aditivitas, area di bawah kurva$S$$$ω = n / t akan sama$\omega = n/t$$$$S_n = n S$ . Pada gilirannya, untuk setiap strip kita dapatkan: $$$S_{n} - S_{n-1} = n S - (n-1)S = S$ .Ternyata perbedaan area tidak tergantung pada "jumlah" hiperbola. Ini bukan sesuatu yang istimewa tentang hiperbola, kesimpulan yang sama dapat ditarik untuk setiap kurva bentuk$$y = n f ( x ) , jika hanya fungsi$y = n f(x)$$$f dapat diukur. Dan jika demikian, maka untuk seluruh area definisi, masuk ke bagian putih diagram atau yang teduh sama-sama memungkinkan, seperti yang diharapkan untuk koin "jujur". Argumen yang baru saja kita kutip tampak cukup sederhana, tetapi mereka memberikan hasil yang sangat umum, berlaku untuk jumlah aditif apa pun. Konsep abstrak ukuran memungkinkan kita untuk membandingkan jumlah tak berujung di antara mereka sendiri, sambil tetap berada dalam kerangka logika dan akal sehat. Abstraksi itu baik, tetapi dapat dikatakan bahwa pada kenyataannya kita tidak melempar koin dengan semua parameter yang mungkin. Seperti yang ditunjukkan oleh percobaan dengan kamera kecepatan tinggi, kecepatan sudut jatuh dalam kisaran dari$f$



$$20 hingga$20$$$40 putaran per detik, dan durasi penerbangan dari setengah hingga satu detik. Area ini disorot oleh segi empat dalam diagram. Di dalamnya, total area dari garis-garis putih sedikit lebih besar daripada yang oranye, dan kita dapat menyimpulkan bahwa kemungkinan jatuh dari sisi yang sama yang selama lemparan$40$$$$50.6\%$ .

Pada 2007, sekelompok Percy Deaconess et al dari Stanford menerbitkan sebuah artikel yang memberikan analisis terperinci tentang proses membalik koin. Penjelasan terperinci tentang mekanisme piringan terbang dan berputar, yang tidak hanya berputar, tetapi juga precesses - sumbu rotasi itu sendiri berputar dalam penerbangan, menunjukkan bahwa dengan manual melemparkan dari posisi "elang dari atas", probabilitas "elang" yang jatuh dengan seperseratus lebih dari setengah.

Apakah banyak atau sedikit? Berapa banyak percobaan yang Anda butuhkan untuk membuat perbedaan? Ketika data eksperimental terakumulasi, kesalahan standar rata-rata, yang mencerminkan kesalahan yang dengannya nilai rata-rata dapat dihitung, menurun secara proporsional dengan akar kuadrat dari jumlah tes:$$σ μ = σ / √di sini$\sigma_{\mu} = \sigma/\sqrt{n}$$$σ adalah standar deviasi untuk distribusi yang diteliti. Dalam kasus kami, untuk distribusi Bernoulli dengan probabilitas$\sigma$$$0,51 yang sama$0.51$$$$\sqrt{0.51\times0,49}\approx0.5$ . Untuk dengan yakin mengidentifikasi penyimpangan rata-rata seperseratus, penyimpangan ini harus melebihi $$3 standar deviasi. Dengan demikian, kita dapat memperkirakan jumlah uji coba:$3$

$$

$$n = \left(\frac{\sigma}{\sigma_{\mu}}\right)^2 = \left(\frac{3\times0.5}{0.01}\right)^2 \approx 22500$$

Berkali-kali Anda perlu membalik koin untuk memperhatikan penentuan mekanistik dari hasilnya. Untuk memperjelas apa yang dimaksud, saya akan memberikan contoh dua ratus tes "koin" ideal dan sedikit tidak sempurna yang dilakukan untuk menghitung kemungkinan hilangnya, misalnya, seekor elang. Setiap tes terdiri dari$$40.000 lemparan. Kata-kata "koin" dan "lemparan" ada dalam tanda kutip, karena pada kenyataannya, bukan koin fisik yang digunakan, tetapi generator nomor acak yang mematuhi distribusi Bernoulli.$40000$

Eksperimen dengan melempar koin yang ideal dan sedikit tidak sempurna untuk memperbaiki ketidaksempurnaan.

Terlihat hanya setelah itu$$20.000 tes "awan" dari nilai rata-rata yang diamati mulai terpisah dengan jelas. Nah, untuk penggunaan domestik, kita dapat mengasumsikan bahwa koin adalah generator yang baik dari pilihan acak dari dua opsi yang sama-sama mungkin.$20000$

Hukum turis

Kesetaraan penentuan frekuensi geometris dan probabilitas mengungkapkan misteri satu hukum kekejaman, yang dikenal di kalangan wisatawan, ahli geologi dan semua orang yang menggunakan peta topografi:

Tempat di mana turis pergi paling sering di lipatan peta atau di tepi lembaran.

Misalkan kita sama-sama sering tertarik pada objek yang terletak di semua bagian peta. Tetapi kita jarang tertarik pada objek tanpa ukuran - seluruh titik menggunakan peta adalah untuk mensurvei sekitar objek, yaitu, beberapa area terbatas. Biarkan sebagian kecil sudah cukup bagi kita$$α dari area seluruh peta$\alpha$$$S untuk mencari cara untuk sampai ke objek. Jadi, jika objek mendekati tikungan atau tepi pada jarak kritis$S$$$d , kami akan mempertimbangkan hukum turis terpenuhi. Bagian wilayah perbatasan di area total peta akan memberi kita kesempatan untuk mengalami hukum kekejaman ini pada diri kita sendiri. Inilah tampilan bagian peta yang tidak menyenangkan saat itu$d$$$α = 0,5 % dan dalam satu tikungan.$\alpha=0.5\%$

Gray menunjukkan area "buruk". Secara terpisah menunjukkan sebagian dari daerah setengah poin dari kartu lebar 40 cm, memiliki diameter sedikit lebih besar dari 3 cm.

Untuk kartu persegi$$$d = \sqrt{\alpha S}$ . Potongan tidak menyenangkan akan memiliki area $$$d \sqrt{S} = S\sqrt{\alpha}$ .Empat garis, dua vertikal dan dua horisontal, akan terletak di tepi, setiap tikungan tambahan, horizontal atau vertikal, akan menambah strip lain. Pada saat yang sama, strip berpotongan menambahkan kotak tambahan dengan area$$$d^2 = \alpha S$ . Dengan melipat kartunya sehingga ternyata $$$n$ horisontal dan $$$m$ tikungan vertikal, kami mendapatkan luas total zona tidak menyenangkan yang sama dengan: $$$S (n + 2) \ sqrt {\ alpha} + S (m + 2) \ sqrt {\ alpha} -S (n + 2) (m + 2) \ alpha$ . Membawanya ke area seluruh peta, kami mendapat bagian yang tidak menyenangkan dari total area:

$$

$$p = (n + m + 4) \ sqrt {\ alpha} - (n + 2) (m + 2) \ alpha.$$

Gambar tersebut menunjukkan area di mana proporsi ini melebihi $$$50 \%$ untuk berbagai nilai $$$\ alpha$ .

Area di mana ada kemungkinan peningkatan berada di lipatan peta atau di tepinya. Angka menunjukkan fraksi dari area yang dianggap lingkungan dari area seluruh peta.

Ternyata kartu yang dilipat dua dua kali sudah secara resmi dianggap tidak jujur ​​dalam kaitannya dengan turis. Paling sering, kartu memiliki tiga lipatan horizontal vertikal dan tiga, yang memberikan kemungkinan memenuhi hukum kekejaman dengan probabilitas sekitar $$$60 \%$ di $$$\ alpha = 0,5 \%$

Dari mana datangnya peluang?

Di toko-toko suvenir, Anda dapat menemukan pendulum magnetik untuk "pilihan keinginan." Mereka juga merupakan generator acak mekanis dan kadang-kadang keliru disebut "pendulum kacau". Memulai pergerakan dari beberapa posisi awal dan kecepatan, bandul melakukan serangkaian osilasi “tak terduga” dan akhirnya berhenti di salah satu sektor. Namun, fluktuasi di sini tidak dapat diprediksi, mereka hanya sangat sensitif terhadap kondisi awal. Untuk setiap sektor di mana pendulum dapat berhenti, ada wilayah tarikan di ruang kecepatan koordinat. Ini adalah seperangkat kondisi awal di mana pendulum akan menarik ke titik tertentu di sektor yang ditunjukkan. Titik henti pendulum disebut sebagai penarik - titik menarik. Dalam kasus pendulum dari gambar, ruang koordinat dan kecepatan adalah empat dimensi, sehingga tidak mudah untuk menunjukkan area tarikan. Tetapi jika kita membatasi diri hanya pada dua sektor dan mengurangi masalah menjadi satu dimensi (pendulum seperti itu disebut osilator Duffing), maka ruang nilai awal akan berubah menjadi sebuah pesawat, sehingga daerah objek wisata dapat dilihat. Mereka tampak seperti simbol Yin-Yang yang rumit, dengan cepat berubah menjadi garis-garis sempit yang memisahkan bidang-bidang daya tarik.

Area daya tarik penarik untuk pendulum keinginan satu dimensi - osilator Duffing.

Seperti dalam kasus koin, sedikit mengubah kondisi awal, kita dapat dari satu penarik ke penarik lainnya. Dadu dan roulette bekerja dengan cara yang sama, tetapi mereka sendiri bukan generator acak. Ini bukan sistem yang benar-benar kacau dan perilaku mereka dapat dihitung secara akurat.

Tapi apa itu peluang nyata? Contoh yang baik dari sistem stokastik sejati adalah penampilan mobil di jalan. Orang tidak setuju, tidak mengoordinasikan rencana mereka, setiap elemen dari ansambel di luar jalan bertindak secara independen. Dan meskipun ada pola tertentu dalam perilaku orang - jam sibuk di pagi dan sore hari, jalan kosong di malam hari, dll., Kita tidak memiliki dan tidak akan pernah memiliki informasi yang cukup tentang setiap peserta dalam gerakan untuk memprediksi penampilan mereka. Mekanika partikel elementer di tingkat kuantum, peluruhan atom yang tidak stabil, perubahan kode genetik, kemungkinan besar, gempa bumi dan harga saham di bursa saham juga bersifat stokastik. Satu-satunya hal yang tersisa bagi peneliti adalah menganggap mereka sebagai variabel acak dan menggambarkannya dalam hal teori probabilitas.

Tapi ada sumber peluang lain - kekacauan dinamis . Sistem chaotic berbeda dari yang stokastik dalam hal mereka digambarkan oleh persamaan dan parameter yang tidak mengandung keacakan. Namun, perilaku mereka tidak hanya rumit, tetapi kacau dan benar-benar tidak dapat diprediksi. Jika kita mulai menggoyangkan pendulum keinginan, dengan sangat hati-hati, dengan frekuensi dan amplitudo yang terkontrol dengan baik, kita akan menemukan bahwa gerakannya yang halus tidak dapat dihitung untuk waktu yang lama. Tidak ada algoritma pada komputer yang akurat dan sewenang-wenang yang akan memungkinkan kami untuk menghitung perilaku pendulum yang tepat untuk masa depan yang jauh secara sewenang-wenang. Dia tidak akan berhenti di sektor apa pun, tetapi akan membuat gerakan halus, tetapi dia tidak akan pernah kembali ke titik yang sama di ruang kecepatan koordinat dua kali. Contoh lain dari sistem kacau yang sangat sederhana adalah bola ideal yang memantul di medan gravitasi di atas meja ideal dengan pegas. Persamaan Lorentz yang relatif sederhana menunjukkan bahwa kita tidak pernah dapat memprediksi cuaca selama lebih dari beberapa minggu - ini juga merupakan sistem yang kacau.

Teori kekacauan dinamis mampu menjelaskan sifat ketidakpastian seperti itu. Pendulum keinginan satu dimensi yang sederhana, yang kami kaji, memiliki dua titik stasioner yang stabil - dua penarik, dan satu tidak stabil, dari mana sistem berusaha untuk melarikan diri, itu ditunjukkan oleh lingkaran putih. Dalam mode kacau, alih-alih satu set penarik, jumlah lintasan stasioner tidak stabil yang tak terbatas muncul dalam sistem. Himpunan ini tidak terbatas, tetapi memiliki ukuran nol , dan merupakan struktur terpisah yang sangat rumit. Setelah berada di salah satu lintasan ini, pada prinsipnya tidak mungkin untuk mengikutinya menggunakan algoritma terbatas. Tetapi yang paling mengejutkan, ternyata jumlah lintasan tidak stabil yang tak terbatas ini menarik! 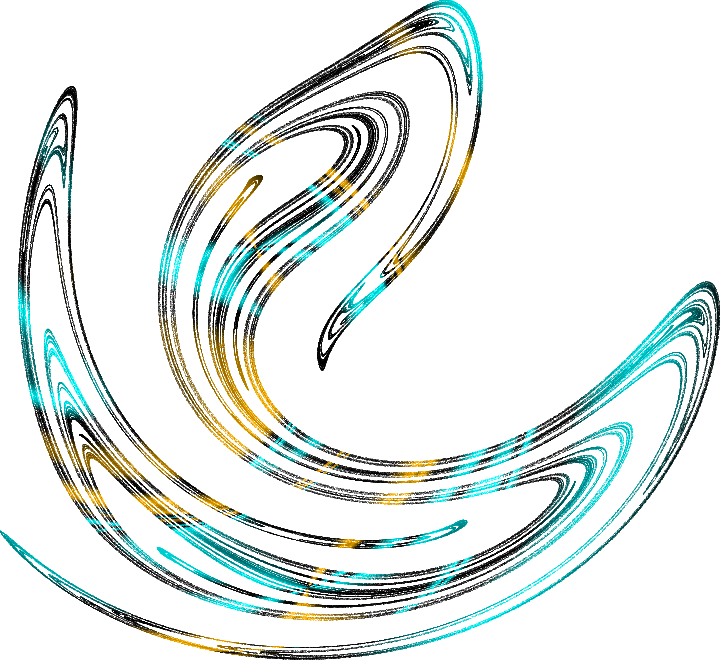Sistem kacau terus-menerus melompat dari sekitar satu lintasan yang tidak stabil ke lintasan yang lain, sambil tetap berada dalam batas-batas penarik aneh ini. Jadi set ini disebut: penarik aneh . Ini adalah bagaimana bagian dari penarik aneh untuk pendulum keinginan, tunduk pada osilasi harmonis, terlihat sangat indah. Objek ini untuk pendulum satu dimensi dapat dijelaskan dalam ruang tiga dimensi (koordinat, kecepatan, fase osilasi paksa). Jika Anda memotong penarik di ruang ini dengan pesawat, Anda dapat melihat strukturnya, ini disebut bagian Poincare . Setiap titik di sini adalah jejak lintasan, dan warna titik-titik mencerminkan kecepatan relatif yang dengannya lintasan saling berhamburan. Berikut adalah beberapa penarik aneh yang cantik:


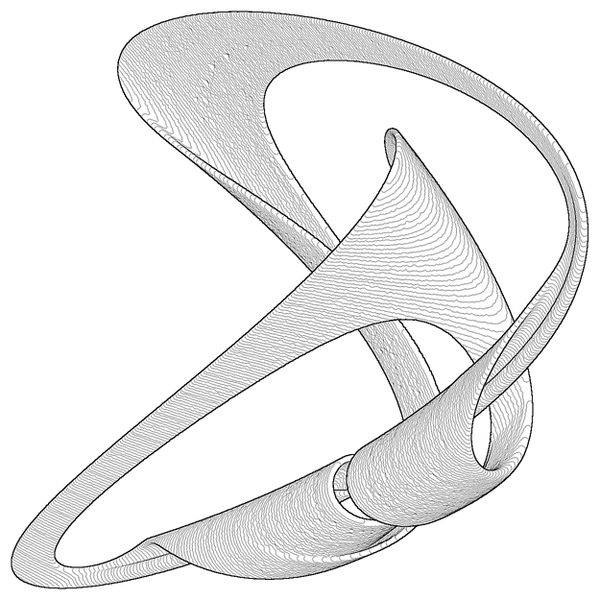Kiri: Bagian Poincare untuk lintasan bola memantul di atas meja pegas. Banyak titik milik permukaan bola sesuai dengan hukum kekekalan energi. Kanan: daerah volumetrik yang membungkus penarik aneh yang dilahirkan selama getaran paksa dari pelat tebal.

Kelancaran lintasan kacau memungkinkan Anda untuk melihat sedikit ke masa depan. Ini menjelaskan satu pengamatan yang menjengkelkan: di satu sisi, peramal cuaca kadang-kadang tidak percaya diri dapat memprediksi cuaca selama seminggu, tetapi di sisi lain, jika Anda mengatakan bahwa besok akan menjadi cuaca yang sama seperti hari ini, maka Anda tidak akan salah dalam sekitar tiga dari empat kasus. . Secara umum, lelucon tentang peramal cuaca tidak adil dan kita harus menghargai pikiran dan ketekunan manusia, yang memungkinkan untuk memprediksi cuaca di tingkat modern!

Kekacauan yang dinamis sangat kompleks dan indah sebagai teori, ini menimbulkan gambar keanggunan yang luar biasa, tetapi juga bisa berguna. Misalnya, algoritma yang digunakan angka acak di komputer juga bersifat deterministik. Untuk contoh-contoh dalam buku ini, saya menggunakan generator bilangan pseudo-acak yang tidak memulai proses stokastik nyata (peluruhan alfa, atau menghitung mobil di jalan), tetapi menghitung angka "acak" berikutnya berdasarkan yang sebelumnya diterima sebelumnya.

Dari koin hingga kupu-kupu dan nasib sendiri

Pengamatan bagaimana penyimpangan kecil tumbuh menjadi perubahan global dalam sistem menyebabkan pemikiran tentang "efek kupu-kupu". Biarkan saya mengingatkan Anda bahwa efek ini berarti rantai konsekuensi dramatis yang luas dari beberapa peristiwa yang tidak signifikan, pada pandangan pertama. Hancur oleh para peneliti di masa lalu, kupu-kupu dalam cerita pendek Ray Bradbury "And the Thunder hit" menyebabkan restrukturisasi radikal masa depan. Dan salah satu ceramahnya, Edward Lorenz, pencipta teori kekacauan dinamis, berjudul: "Bisakah kepakan sayap kupu-kupu di Brasil menyebabkan tornado di Texas?"

Kami secara implisit merujuk pada efek ini, meratapi: "Jika saya tidak berbelok, semuanya akan berbeda!", "Jika dia tidak naik kereta ini, tidak akan ada bencana!" atau "Karena hal-hal sepele seperti itu, mereka bertengkar dan berpisah !!" Tetapi kita melihat bahwa dunia kuantum yang benar-benar stokastik dan jam atom ultra-presisi hidup berdampingan di dunia, sistem Hamilton yang stabil di dunia bintang dan galaksi dan kekacauan cincin Saturnus atau cincin Kuiper, gerakan termal molekul dan akurasi yang luar biasa dari pengoperasian sistem biologis atau mekanisme mobil. Tidak, kepakan sayap kupu-kupu tidak menimbulkan badai, tetapi menghilang tanpa jejak, memunculkan rantai vortisitas yang mentransmisikan energi dan informasi ke vortisitas yang semakin kecil, sampai energi dan informasi menghilang dalam kekacauan fluktuasi. Harus dipahami dengan jelas bahwa penyimpangan kecil mengarah pada reorganisasi mendasar sistem hanya jika tidak stabil atau jika sistem berada di ambang bifurkasi atau malapetaka - inilah yang disebut restrukturisasi global dalam perilaku sistem dengan perubahan kecil dalam parameter yang disebut dalam bahasa matematika. Dan bifurkasi selalu membentuk set ukuran nol di ruang parameter - ini adalah titik atau batas. Gangguan kecil tidak mengarah ke bencana hampir di mana-mana (ini juga merupakan istilah yang tepat yang berarti "di mana-mana, kecuali untuk seperangkat ukuran nol"), dan keadaan yang tidak stabil di alam jarang diamati tanpa melewati "ujian waktu".

Jika pasangan itu putus “karena omong kosong”, dia ditakdirkan untuk putus dalam hal apa pun, dia tidak stabil. Pasangan yang stabil melewati perang dan kelaparan, dan kemudian, kadang-kadang, mereka putus, tetapi bukan karena hal-hal sepele, tetapi sebagai hasil dari perubahan mendalam yang dapat terjadi pada seseorang selama hidupnya. Dalam rangkaian peristiwa yang menyebabkan kecelakaan kereta api, tidak mudah untuk memilih peristiwa utama (kesalahan spesifik atau kecelakaan fatal) dan, kemungkinan besar, kuncinya bukan peristiwa, tetapi pelanggaran sistematis terhadap peraturan, yang menyebabkan sistem ke keadaan yang tidak stabil. Jika ada banyak parameter dalam sistem, dan beberapa di antaranya adalah acak, dan kehidupan kita terstruktur seperti itu, maka informasi dalam sistem seperti itu cenderung hilang, dan tidak mungkin untuk memulihkan pada saat yang tepat dalam hidup kita "semuanya salah." Jangan menyiksa diri sendiri dengan penyesalan tentang apa yang terjadi, tetapi perhatikan lebih dekat apa yang terjadi pada Anda sekarang, agar tidak ketinggalan titik bifurkasi yang sebenarnya.

Dalam hal ini, kita dapat mengingat salah satu hukum merfologi, yang disebut hukum restorasi oleh Dreisen tertentu:

Waktu untuk memperbaiki situasi berbanding terbalik dengan waktu memburuk.

Pengamatan berikut diberikan sebagai contoh: Butuh waktu lebih lama untuk merekatkan vas daripada mematahkannya. Undang-undang ini secara mengejutkan secara akurat menggambarkan hubungan antara tingkat karakteristik untuk proses relaksasi sistem yang stabil, yang dapat dijelaskan oleh hukum eksponensial yang menurun $$$e ^ {- \ lambda t}$ dan laju perkembangan proses bencana dalam sistem yang tidak stabil, dalam pendekatan linier - pertumbuhan eksponensial dari gangguan kecil $$$e ^ {\ lambda t}$ . Kecepatan ini memang berbanding terbalik satu sama lain. Contoh vas, bagaimanapun, bukanlah relaksasi - transisi ke keadaan yang paling memungkinkan. Ini lebih dekat ke proses lain - untuk mengatur diri sendiri , proses ini, sebagai pendekatan pertama, dijelaskan oleh hukum logistik dan lebih cepat dalam kecepatan untuk relaksasi daripada bencana.

Proses non-stasioner yang khas: bencana, relaksasi, dan pengaturan diri, memiliki waktu karakteristik yang sama.

$$

$$* * *$$

Terkadang, berjalan di salju, aku terkejut bahwa kepingan salju jatuh di hidungku. Saya terkejut bahwa kemungkinan acara ini dapat diabaikan. Dilihat oleh itu, dia dilahirkan tinggi di langit di atas Samudra Pasifik, dilingkari dalam arus turbulen yang tidak menentu di awan, jatuh terus-menerus mengubah arah ... untuk sampai ke ujung hidungku! Dan betapa menakjubkannya perjalanan foton dari bintang yang jauh !? Selama puluhan ribu tahun mereka bergegas melintasi Semesta, mereka tidak ditelan debu, mereka tidak bertemu asteroid! Mereka lahir di dunia kuantum bintang jauh, dan mengakhiri perjalanan mereka di dunia kuantum protein opsin di retina di mata saya. Tidak ada gunanya bahkan mempertimbangkan probabilitas dari peristiwa ini, itu adalah nol, tetapi peristiwa itu terjadi, dan saya melihat cahaya bintang yang berkedip-kedip. Sekarang jelas bahwa ini semua karena area hidungku dan bahkan molekul-molekulnya memiliki ukuran yang tidak nol, tetapi masih menakjubkan: apa yang hampir pasti tidak seharusnya terjadi masih terjadi!

Biarkan para filsuf berdebat tentang nasib yang telah ditentukan atau tidak disengaja, kebenaran atau bayangan pengetahuan kita tentang alam. Saya mendesak pembaca untuk melihat dunia dari ketinggian abstraksi matematika dan mengagumi keindahan dan konsistensinya.