Logika bernilai tiga
Daftar pencapaian
- Gerbang logika ternary dasar: T_NOT, T_OR, T_AND, T_NAND, T_NOR, T_XOR, dan lainnya
- Sintesis, Minimisasi dan Realisasi untuk Fungsi Ternary
- Setengah adder ternary, Adary penuh adder, Adary ternary ripple carry
- Subtractor penuh penuh, komparator, multiplier, multiplexer / demultiplexer
- Flip flap jepit dan kait ternary
- Unit Aritmatika dan Logistik Ternary (ALU) primitif
Konvensi dan teknologi yang digunakan
- Unbalanced Ternary (0, 1, 2) digunakan dalam implementasi
- 1 Trit dinyatakan oleh 2 Bits: 0 ~ 00, 1 ~ 01, 2 ~ 10 (11 tidak ditentukan)
- ModelSim, Quartus prime, Logisim
Pendahuluan
Sebagai mahasiswa tahun pertama dari Innopolis University, kami memiliki kesempatan untuk merealisasikan proyek di seluruh kursus arsitektur komputer kami. Kelompok kami sangat tertarik dengan sistem terner dan fungsinya, jadi kami memutuskan untuk menerapkan sistem terner sederhana dengan komponen dasar (gerbang).
Dalam logika, logika tiga nilai (juga logika triner, trivalen, ternary) adalah salah satu dari beberapa sistem logika bernilai tinggi di mana ada tiga nilai kebenaran yang menunjukkan nilai ketiga benar, salah, dan beberapa tidak pasti.
Logika ternary sesuai dengan MVL (Logika bernilai banyak). Namun, hanya tiga keadaan logika yang digunakan, ' 0 ', ' 1 ' dan ' 2 '. Radix ( r ) optimal dari bilangan pecahan ditemukan sebagai logaritma natural ( e ). Logika ternary menggunakan representasi angka dengan r = 3 , dibandingkan dengan logika biner yang menggunakan r = 2 , maka bilangan bulat integer paling ekonomis yang paling dekat dengan logaritma natural e , adalah basis 3. Properti khusus ini dari basis 3 mengilhami komputer awal desainer untuk membangun komputer ternary.
Komputer ternary pertama yang berfungsi dibangun di Rusia di Moscow State University pada tahun 1958. Komputer ini dirancang oleh Nikolay Brusentsov dan rekan-rekannya. Mereka menamakannya Setun , seperti sungai yang mengalir di dekat kampus universitas.
Logika ternary
Fungsi logika terner adalah pemetaan F: {0,1,2} n -> {0,1,2} . Kami akan membahas kelebihan dan kekurangan logika terner daripada logika biner.
Di mana logika Boolean memiliki 2 2 = 4 operator unary, penambahan nilai ketiga dalam logika ternary mengarah ke total 3 3 = 27 operator yang berbeda pada nilai input tunggal. Demikian pula, di mana logika Boolean memiliki 2 2 2 = 16 operator biner yang berbeda (operator dengan 2 input), logika ternary memiliki 3 3 2 = 19.683 operator tersebut. Di mana kita dapat dengan mudah menyebutkan fraksi signifikan dari operator Boolean (bukan, dan, atau, nand, atau, eksklusif atau, ekivalensi, implikasi), tidak masuk akal untuk mencoba menyebut semua kecuali sebagian kecil dari operator ternary yang mungkin.
Keuntungan Logika Ternary
Representasi logika ternary memungkinkan penyandian informasi yang lebih kompak dan efisien daripada representasi logika biner yang setara. Argumen yang dinyatakan adalah sebagai berikut: jika kita mengasumsikan bahwa sirkuit digital memiliki kombinasi input N yang mungkin, maka sirkuit biner memerlukan log 2 jalur input N dan sirkuit terner membutuhkan jalur input log 3 N.
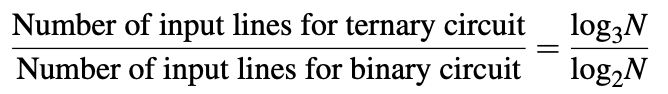

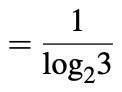

Oleh karena itu, implementasi pengkodean terner dari fungsi logika biner yang diberikan harus membutuhkan 0,63 kali garis input daripada implementasi biner yang sesuai.
Kerugian Logika Ternary
Meskipun sirkuit logika ternary harus memerlukan jalur input yang lebih sedikit daripada sirkuit logika biner yang setara, sirkuit logika ternary saat ini bukan pilihan yang praktis. Alasannya adalah
- Teknologi implementasi perangkat keras ternary masih dalam level teoritis, simulasi, dan uji laboratorium
- Mewakili tiga level logika terner (0, 1, dan 2) menggunakan level voltase dari teknologi yang ada belum didefinisikan secara efektif
- Tidak ada model komputasi dan bahasa pemrograman yang dikembangkan. Namun, mensimulasikan hasil implementasi rangkaian terner menggunakan semikonduktor oksida logam komplementer (CMOS), diode resonansi tunneling (RTD), dan teknologi tabung nano karbon, menunjukkan bahwa logika terner mungkin menjadi pilihan untuk komputasi masa depan.
Berbagai kemungkinan representasi untuk sistem ternary
- Sistem angka ternary (ternary tidak seimbang) , setiap digit adalah trit (trinary digit) yang memiliki nilai: 0, 1, atau 2
- Ternary seimbang , setiap digit memiliki salah satu dari 3 nilai: −1, 0, atau +1; nilai-nilai ini juga dapat disederhanakan menjadi -, 0, +, masing-masing (paling sering digunakan)
- Representasi biner redundan , setiap digit dapat memiliki nilai −1, 0, 0/1 (nilai 0/1 memiliki dua representasi berbeda)
- Sistem angka biner miring , hanya digit non-nol paling signifikan yang memiliki nilai 2, dan digit lainnya memiliki nilai 0 atau 1
Lebih lanjut tentang Sistem Penomoran Ternary yang seimbang
Saat ini, sebagian besar semua perangkat keras dirancang untuk komputasi biner. Jika kita memiliki komponen elektronik yang stabil dengan tiga keadaan stabil, dunia mungkin akan beralih ke komputasi ternary. Namun, ini bukan kebenaran hari ini. Notasi radix terner seimbang memiliki beberapa sifat yang bermanfaat:
- Pembalikan ternary mudah, cukup tukar −1 dengan 1 dan sebaliknya. Jika kita menggunakan contoh, 24 direpresentasikan sebagai 1T0, dan -24 sebagai T10 dalam notasi ternary seimbang (T hanyalah notasi untuk -1). Ini lebih sederhana daripada aturan untuk komplemen keduanya dalam logika biner.
- Tanda angka diberikan oleh 'nol' bukan nol yang paling signifikan
- Operasi pembulatan ke bilangan bulat terdekat identik dengan pemotongan.
- Penambahan dan pengurangan pada dasarnya adalah operasi yang sama (Yaitu Anda hanya menambahkan digit menggunakan aturan untuk penambahan angka)
Contoh:
21 10 = 1T10 3 ; 296 10 = 11T00T 3 ;
-24 10 = T10 3 ; -137 10 = T110T1 3
Aritmatika ternary
Aritmatika ternary dapat menawarkan notasi yang lebih ringkas daripada aritmatika biner, dan akan menjadi pilihan yang jelas jika produsen perangkat keras akan menemukan saklar ternary.
Penambahan dan Multiplikasi Ternary yang Seimbang
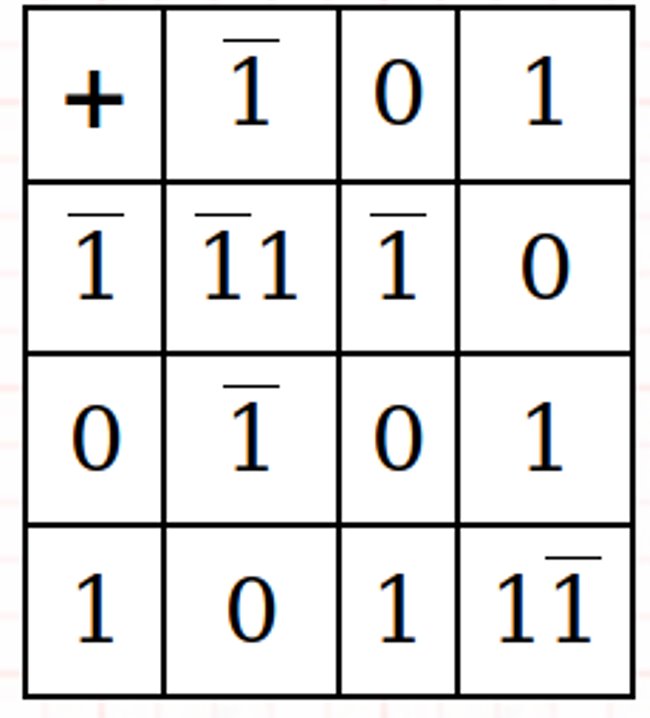
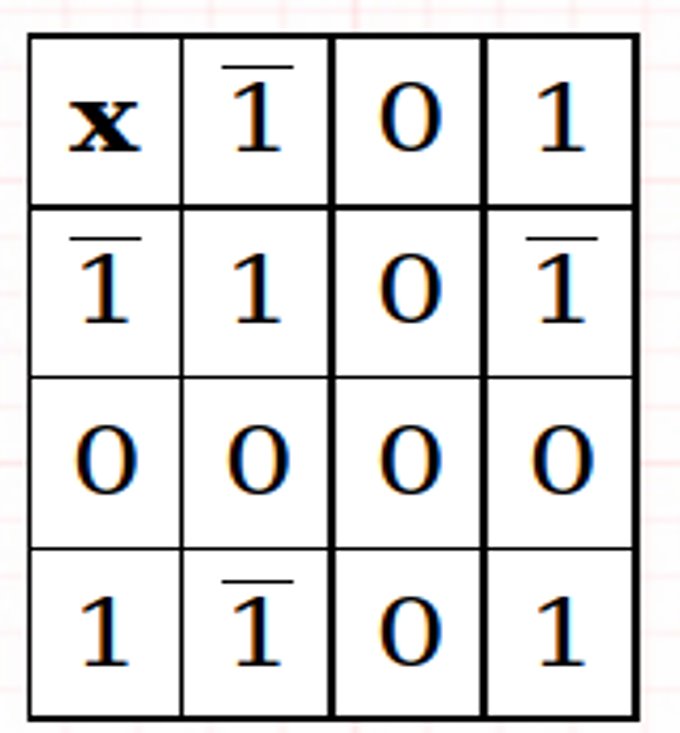
Contoh:
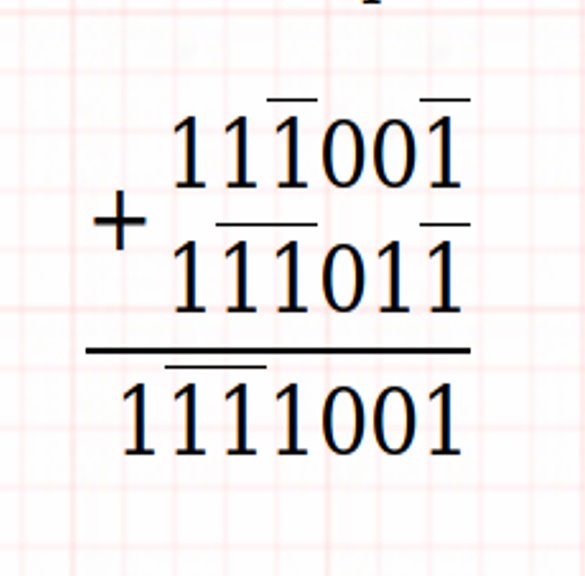
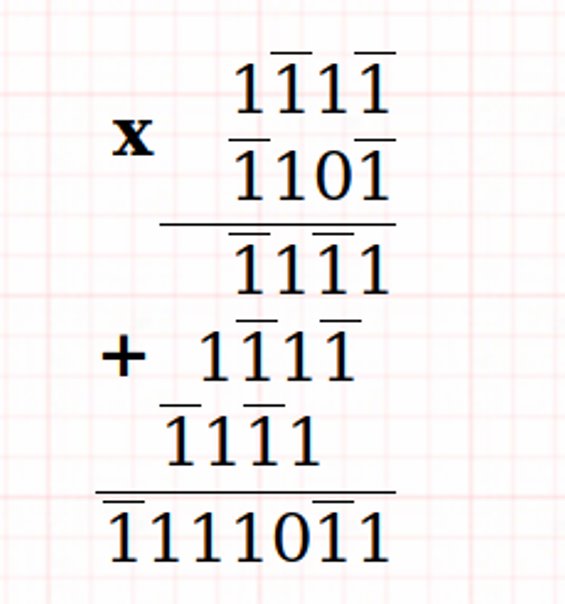
Sirkuit kombinasional ternary (Gerbang Ternary)
Sirkuit kombinasional terdiri dari variabel input, gerbang logika ternary dan variabel output. Output dari sirkuit hanya bergantung pada input yang ada. Gerbang logika menerima sinyal dari variabel input dan menghasilkan sinyal output. Proses ini mengubah informasi terner dari
input data yang diberikan ke data output ternary yang diperlukan.
Seperti yang disebutkan di atas, kita dapat dengan mudah menyebutkan fraksi signifikan dari operator Boolean (bukan, dan, atau, nand, atau, eksklusif atau, ekivalensi, implikasi), namun, tidak masuk akal untuk mencoba menyebut semua kecuali sebagian kecil dari kemungkinan operator ternary. Kami akan mempertimbangkan sirkuit terner berikut:
Dan (Min) : Wajar untuk memperluas Boolean dan fungsinya menjadi fungsi ternary dengan menyatakan bahwa hasilnya hanya benar jika kedua input benar, salah jika ada input salah, dan tidak diketahui sebaliknya.
Dan sirkuit / tabel kebenaran Atau (Maks) : Adalah wajar untuk memperluas Boolean atau fungsi ke ternary dengan menyatakan bahwa hasilnya benar jika input apa pun benar, salah hanya jika kedua input salah, dan tidak diketahui sebaliknya.
Atau sirkuit / tabel kebenaran Konsensus : Dalam logika Boolean, kebalikan dari eksklusif atau benar ketika dua input sama, dan salah ketika mereka berbeda. Ada beberapa ekstensi alami dari ide ini ke logika terner. Salah satunya adalah konsensus logis dari satu set variabel, yang benar jika semuanya benar, salah jika semuanya salah, dan sebaliknya tidak diketahui
Sirkuit konsensus / tabel kebenaran Any : Jika konsensus mensyaratkan bahwa kedua input setuju sebelum menyatakan sesuatu tetapi tidak diketahui, operator menerima apa pun menyatakan kesimpulan yang tidak diketahui hanya jika kedua input tersebut tidak diketahui atau secara aktif tidak setuju. Jika tidak, ia akan mengambil kesimpulan dari input yang tidak dikenal yang tersedia untuknya.
Setiap tabel sirkuit / kebenaran Peningkatan dan Penurunan : Dalam logika Boolean, inverter dapat dianggap sebagai penambahan atau penurunan argumen modulo 2. Logika internal, fungsi penambahan dan penurunan modulo 3 cukup berbeda dari inversi.
Sirkuit kenaikan dan Penurunan Sintesis, Minimisasi dan Realisasi untuk Fungsi Ternary
Hubungan saling terkait dalam sistem logika terner
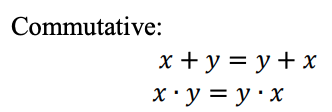
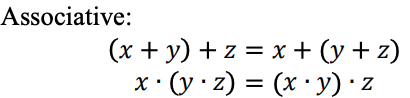
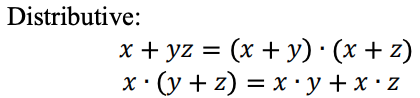
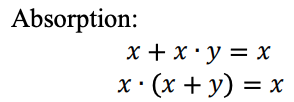
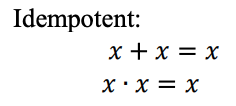
Fungsi logika ternary dapat direpresentasikan sebagai ekspresi Max-Min. Ekspresi Max-Min Ternary didefinisikan sebagai berikut:
Variabel : Setiap simbol yang mengambil nilai dari set T ∈ {0,1,2} adalah variabel ternary.
Literal : Literal adalah bentuk-bentuk variabel yang diubah. Mereka digunakan untuk membentuk ekspresi Max-Min.
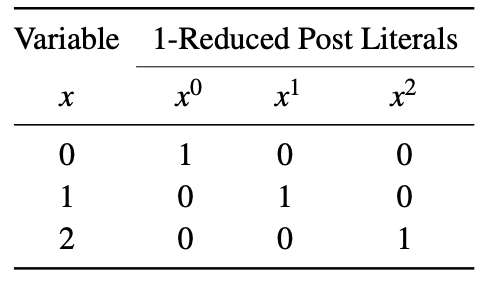
Dalam literatur dua jenis literal umumnya digunakan: 1-berkurang Post literal dan 2-berkurang post literal. Post literal 1-tereduksi dari variabel x direpresentasikan sebagai x i , di mana i ∈ {0,1,2}. Ketika x = i, maka x i = 1, jika tidak x i = 0. Liter 1 Post yang dikurangi dari suatu variabel ditunjukkan di bawah ini.
Post literal 2-reduksi dari variabel x direpresentasikan sebagai x i , di mana i ∈ {0,1,2}. Ketika x = i, maka x i = 2, jika tidak x i = 0. Liter 2 Post yang dikurangi dari suatu variabel ditunjukkan di bawah ini. Contoh ini menggunakan set literal yang berbeda untuk membentuk ekspresi Max-Min seperti yang dibahas sebelumnya.
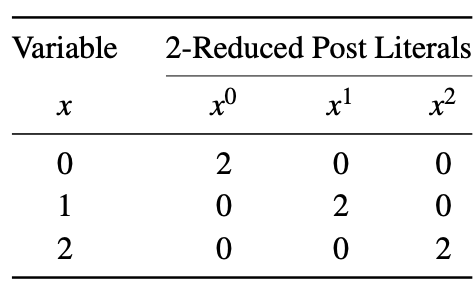
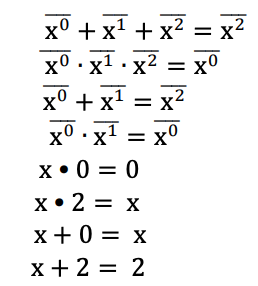
Minterm : Ketika literal variabel suatu fungsi digabungkan menggunakan operasi Min, maka istilah itu disebut minterm. Sebagai contoh, untuk fungsi logika ternary 3-variabel F (x, y, z), xyz dan xz adalah dua contoh minterm.
Ekspresi Maks-Min : Ketika dua atau lebih minterm digabungkan menggunakan operasi Max, maka ekspresi tersebut disebut sebagai ekspresi Max dari minterm (Max-Min). Misalnya, untuk fungsi logika ternary 3-variabel F (x, y, z) = xy + yz + xyz adalah contoh ekspresi Max-Min.
Setiap fungsi F (x, y, z) selalu dapat direpresentasikan sebagai
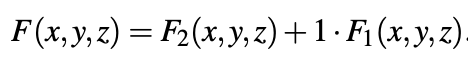
Tiga metode dasar untuk meminimalkan fungsi terner adalah:
- Manipulasi ekspresi aljabar seperti pada aljabar Boolean.
- Metode tabular.
- Metode peta ternary K.
Untuk implementasi sirkuit ternary, perlu untuk mengubah variabel ternary menjadi variabel unary (menggunakan tabel 2-Reduced Post Literals).
Setengah adder ternary
Sirkuit untuk penambahan dua angka 1 trit disebut sebagai setengah penambah. sirkuit tidak mempertimbangkan carry yang dihasilkan pada penambahan sebelumnya. Proses penambahan dalam sistem logika terner ditunjukkan di bawah ini. Di sini A dan B adalah dua input dan jumlah (S) dan carry (CARRY)
dua output.
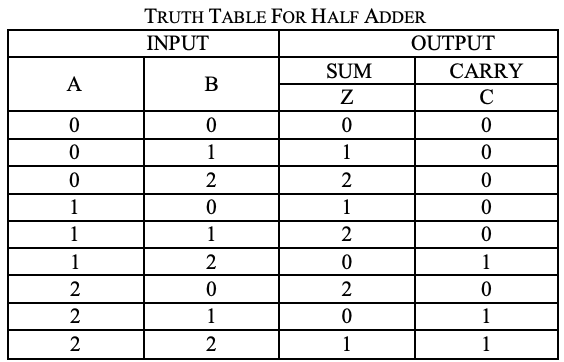
Analisis
Peta karnaugh (K-map) digunakan untuk mewakili jumlah dan membawa output. K-maps berguna untuk meminimalkan dan mengoptimalkan rangkaian logika. Di sini digunakan peta-K dari 2 input. Karena tidak ada pengelompokan 2's dan 1'is mungkin, persamaan output adalah sebagai berikut.
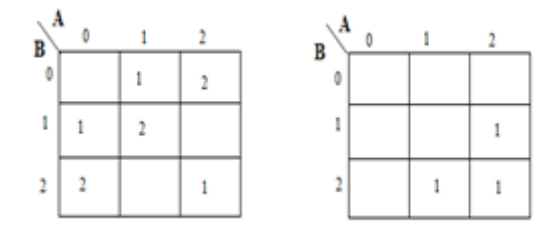
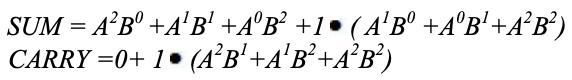
Implementasi
Sirkuit setengah penambah / Verilogmodule half_adder ( input [1:0] A, [1:0] B, output [1:0] sum, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; wire [1:0] c0, c1, c2, c3; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a2,b0,i0); andgate and_2(a1,b1,i1); andgate and_3(a0,b2,i2); // partial products orgate or_1(i0, i1, o0); orgate or_2(o0, i2, o1); // f1 andgate and_4(a1,b0,i3); andgate and_5(a0,b1,i4); andgate and_6(a2,b2,i5); // partial products orgate or_3(i3, i4, o2); orgate or_4(o2, i5, o3); // f2 andgate and_7(o3,temp,o4); // 1.f2 andgate andc_0(a2,b1,c0); andgate andc_1(a1,b2,c1); orgate orc_0(c0,c1,c2); orgate orc_1(c2,i5,c3); andgate andc_2(c3,temp,carry); // carry orgate or_5(o1, o4, sum); // sum endmodule
Penambah penuh ternary
Seperti dengan setengah adders, satu tahap penambah penuh terner dapat dijelaskan oleh tabel numerik yang memberikan jumlah SUM dan menjalankan CARRY sebagai fungsi dari tiga input A, B, bersama dengan carry di C :
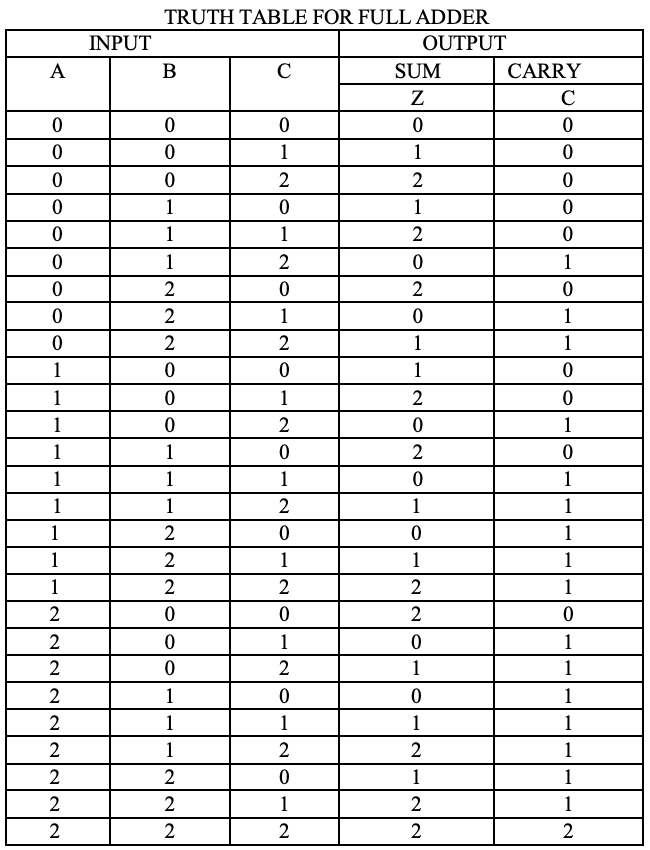
Analisis
Peta karnaugh (K-map) digunakan untuk mewakili jumlah dan membawa output. K-maps berguna untuk meminimalkan dan mengoptimalkan rangkaian logika. Di sini digunakan peta-K dari 3 input.
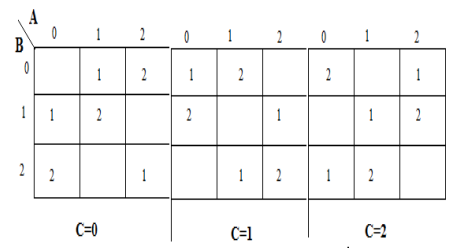
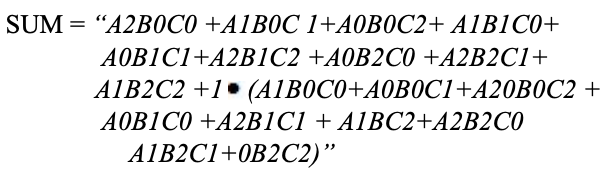
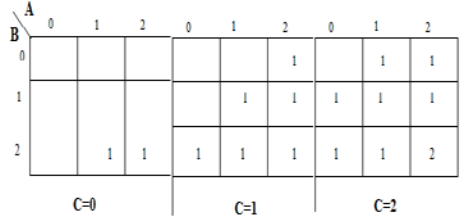
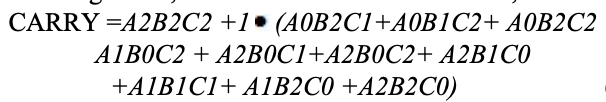
Implementasi
Sirkuit penambah penuh ternary / Verilog module ternary_full_adder ( input [1:0] A, [1:0] B, [1:0] c_in, output [1:0] sum, [1:0] c_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b00; wire [1:0] a0, a1, a2, b0, b1, b2, a20; wire [1:0] i0, i1, i2, i3, i4; wire [1:0] i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] o0, o1, o2, o3, o4, o5, o6, o7, o8, o9; wire [1:0] c0, c1, c2; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12, t13, t14, t15, t16; wire [1:0] g0, g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15; mask mk_1(A, a0, a1, a2); mask mk_2(B, b0, b1, b2); mask mk_3(c_in, c0, c1, c2); andgate3 and3_1(a2,b0,c0, i0); andgate3 and3_2(a1,b0,c1, i1); andgate3 and3_3(a0,b0,c2, i2); andgate3 and3_4(a1,b1,c0, i3); andgate3 and3_5(a0,b1,c1, i4); andgate3 and3_6(a2,b1,c2, i5); andgate3 and3_7(a0,b2,c0, i6); andgate3 and3_8(a2,b2,c1, i7); andgate3 and3_9(a1,b2,c2, i8); andgate3 and3_10(a1,b0,c0, i9); andgate3 and3_11(a0,b0,c1, i10); orgate or__(a2, a0, a20); andgate3 and3_12(a20,b0,c2, i11); // note a20 andgate3 and3_13(a0,b1,c0, i12); andgate3 and3_14(a2,b1,c1, i13); andgate3 and3_15(a1,B,c2, i14); andgate3 and3_16(a2,b2,c0, i15); andgate3 and3_17(a1,b2,c1, i16); andgate3 and3_18(temp2,b2,c2, i17); orgate or_1(i9, i10, o0); orgate or_2(o0, i11, o1); orgate or_3(o1, i12, o2); orgate or_4(o2, i13, o3); orgate or_5(o3, i14, o4); orgate or_6(o4, i15, o5); orgate or_7(o5, i16, o6); orgate or_8(o6, i17, o7); andgate and_1(o7, temp1, o8); // 1.f2 orgate or_9(i0, i1, h0); orgate or_10(h0, i2, h1); orgate or_11(h1, i3, h2); orgate or_12(h2, i4, h3); orgate or_13(h3, i5, h4); orgate or_14(h4, i6, h5); orgate or_15(h5, i7, h6); orgate or_16(h6, i8, h7); orgate or_17_(h7, o8, sum); // sum // carry andgate3 and3_19(a2,b2,c2, t0); // f1 andgate3 and3_20(a0,b1,c2, t1); andgate3 and3_21(a0,b2,c2, t2); andgate3 and3_22(a0,b2,c1, t3); andgate3 and3_23(a1,b2,c0, t4); andgate3 and3_24(a2,b2,c0, t5); andgate3 and3_25(a1,b1,c1, t6); andgate3 and3_26(a1,b2,c1, t7); andgate3 and3_27(a1,b0,c2, t8); andgate3 and3_28(a1,b1,c2, t9); andgate3 and3_29(a1,b2,c2, t10); andgate3 and3_25_(a2,b0,c2, t11); andgate3 and3_26_(a2,b1,c2, t12); andgate3 and3_27_(a2,b0,c1, t13); andgate3 and3_28_(a2,b1,c1, t14); andgate3 and3_29_(a2,b2,c1, t15); andgate3 and3_9_(a2,b1,c0, t16); orgate or_17(t1, t2, g0); orgate or_18(g0, t3, g1); orgate or_19(g1, t4, g2); orgate or_20(g2, t5, g3); orgate or_21(g3, t6, g4); orgate or_22(g4, t7, g5); orgate or_23(g5, t8, g6); orgate or_24(g6, t9, g7); orgate or_25(g7, t10, g8); orgate or_21_(g8, t11, g9); orgate or_22_(g9, t12, g10); orgate or_23_(g10, t13, g11); orgate or_24_(g11, t14, g12); orgate or_25_(g12, t15, g13); orgate or_5_(g13, t16, g14); //f2 andgate and_2(g14, temp1, g15); // 1.f2 orgate or_26(g15, t0, c_out); // carry endmodule
Subtractor penuh ternary
Ternary full-Subtractor adalah sirkuit yang mengurangi dua input dan pinjaman sebelumnya. Tabel kebenaran untuk Subtractor ditunjukkan di bawah ini

Analisis dan Implementasi Pengurangan Penuh Ternary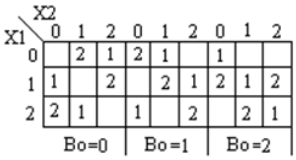
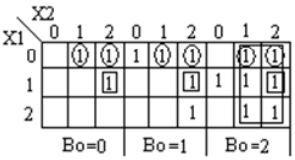
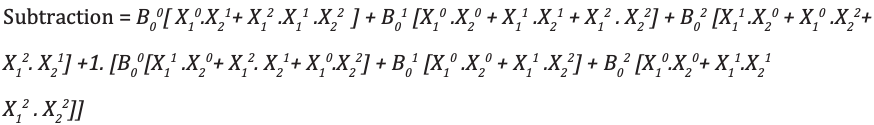
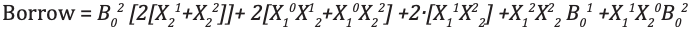
Kode module full_subtractor( input [1:0] P, Q, b_in, output [1:0] diff, b_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b10; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] c0, c1, c2, c3; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7, h8, h9, h10, h11; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9; wire [1:0] p0, p1, p2; wire [1:0] q0, q1, q2; mask mk_1(P, p0, p1, p2); mask mk_2(Q, q0, q1, q2); mask mk_3(b_in, b0, b1, b2); andgate and_0(p0, q1, i0); andgate3 and3_0(p2, p1, q2, i1); orgate or_0(i0, i1, i2); andgate and_1(b0, i2, i3); // first expression andgate and_2(p0, q0, i4); andgate and_3(p1, q1, i5); andgate and_4(p2, q2, i6); orgate or_1(i4, i5, i7); orgate or_2(i7, i6, i8); andgate and_5(i8, b1, i9); // second expression andgate and_6(p1, q0, i10); andgate and_7(p0, q2, i11); andgate and_8(p2, q1, i12); orgate or_3(i10, i11, i13); orgate or_4(i13, i12, i14); andgate and_9(i14, b2, i15); // third expression orgate or_5(i3, i9, i16); orgate or_6(i16, i15, c0); //f1 orgate or_7(i10, i12, t0); orgate or_8(t0, i11, t1); andgate and_10(t1, b0, t2); // 1 expression andgate and_11(p1, q2, i17); orgate or_9(i4, i17, t3); andgate and_12(t3, b1, t4); // 1- expression orgate or_10(i4, i5, t5); orgate or_11(t5, i6, t6); andgate and_12_(t6, b2, t7); // 1-- expression orgate or_12(t2, t4, t8); orgate or_13(t8, t7, t9); andgate and_13(t9, temp1, c1); orgate or_14(c0, c1, diff); // difference orgate or_15(q1, q2, h0); andgate and_14(h0, temp2, h1); andgate and_15(h1, b2, h3); // 1 b orgate or_16(i0, i11, h4); andgate and_16(h4, temp2, h5); // 1- b andgate and_17(i17, temp2, h6); // 1-- b andgate3 and3_1(p2, q2, b1, h7); // 1--- b andgate3 and3_2(p1, q0, b2, h8); // 1---- b orgate or_17(h3, h5, h9); orgate or_18(h9, h6, h10); orgate or_19(h10, h7, h11); orgate or_20(h11, h8, b_out); // borrow endmodule
Riak ternary carry adder
Ripple-carry adder (RCA) adalah sirkuit terkenal untuk melakukan penambahan dua angka oleh cascading ternary full adders. RCA Ternary sangat mirip dengan mitra Binernya. Seorang Half Adder Ternary digunakan untuk menambahkan digit Ternary yang paling tidak signifikan. Sisanya disimpulkan oleh Ternary Full Adders. Seperti disebutkan sebelumnya, Ternary Full Adder menambahkan tiga variabel input Ternary.
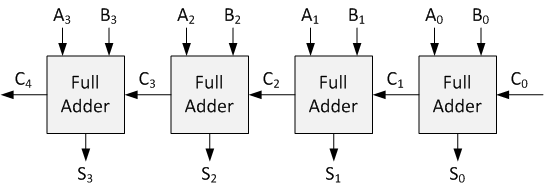
Implementasi
kode Verilog: Ternary ripple carry adder module ternary_ripple_adder ( input [15:0] input1 , input [15:0] input2 , output [15:0] out , output [1:0] overflow_trit ); wire [15:0] carry ; reg tem; assign carry[0] = tem; assign carry[1] = tem; always @(input1, input2) begin tem <= 1'b0; end generate genvar i; for (i = 0; i <= 12; i=i+2) begin full_add af({input1[i+1],input1[i]}, {input2[i+1],input2[i]}, {carry[i+1],carry[i]}, {out[i+1], out[i]}, {carry[i+3],carry[i+2]}); end full_add af({input1[15],input1[14]}, {input2[15],input2[14]}, {carry[15],carry[14]}, {out[15], out[14]}, overflow_trit); endgenerate endmodule
Pembanding ternary
Camper komparator rangkaian ternary dua input X 1 , X 2 dan sesuai menghasilkan output sebagai X 1 = X 2 , X 1 > X 2 , X 1 <X 2 . Tabel kebenaran untuk pembanding ternary ditunjukkan di bawah ini
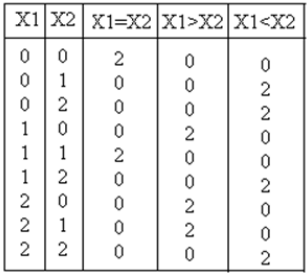
Analisis dan implementasiPersamaan output untuk X 1 = X 2 , X 1 > X 2 , X 1 <X 2 adalah:
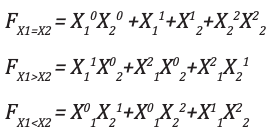
Peta-k yang sesuai ditunjukkan di bawah ini

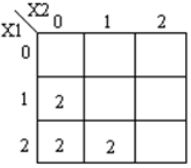
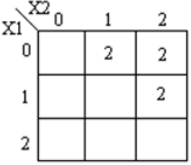
Kode module ternary_comparators ( input [1:0] x1, x2, output [1:0] f1, f2, f3 ); wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7; wire [1:0] h0, h1, h2, h3, h4, h5; wire [1:0] x10, x11, x12; wire [1:0] x20, x21, x22; mask mk_1(x1, x10, x11, x12); mask mk_2(x2, x20, x21, x22); andgate and_0(x10, x20, t0); andgate and_1(x22, x22, t1); orgate or_0(t0, t1, h0); orgate or_1(h0, x11, h1); orgate or_2(h1, x21, f1); // x1 == x2 andgate and_2(x11, x20, t2); andgate and_3(x12, x20, t3); andgate and_4(x12, x21, t4); orgate or_3(t2, t3, h3); orgate or_4(h3, t4, f2); // x1>x2 andgate and_5(x10, x21, t5); andgate and_6(x10, x22, t6); andgate and_7(x11, x22, t7); orgate or_5(t5, t6, h4); orgate or_6(h4, t7, f3); // x1<X2 endmodule
Pengganda ternary
Multiplier ternary adalah sirkuit yang mengalikan dua angka input dan menghasilkan produk yang sesuai. Tabel kebenaran untuk sirkuit ini ditunjukkan di bawah ini:
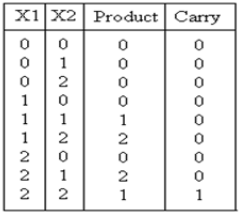
Analisis dan implementasiEkspresi yang dihasilkan untuk produk dan carry ditampilkan:
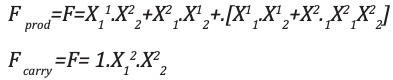
Peta-K yang sesuai ditunjukkan:
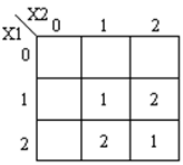
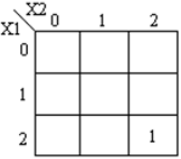
Kode module ternary_multiplier ( input [1:0] A, [1:0] B, output [1:0] product, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a1,b2,i0); andgate and_2(a2,b1,i1); orgate or_1(i0, i1, o0); // f1 andgate and_4(a1,b1,i3); andgate and_5(a2,b2,i4); orgate or_3(i3, i4, o2); andgate and_3(temp,o2,o3); orgate or_4(o3, o0, product); // product andgate andc_0(a2,b2,o4); andgate andc_1(temp,o4,carry); // carry endmodule
Multiplexer dan Demultiplexer Ternary
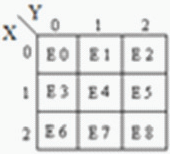
Multiplexer adalah sirkuit yang memiliki banyak input dan output tunggal. Ia juga dikenal sebagai decoder. Fungsi output dari multiplexer ditentukan oleh jumlah garis fungsi. Jadi untuk 2 trit
multiplexer output akan menjadi 3 2 = 9 dan dua akan menjadi fungsi pilih baris. Fungsi multiplexer yaitu
logika seleksi memilih 1 dari 9 fungsi sebagai output. Fungsi pilih logika diimplementasikan menggunakan gerbang logika. Persamaan output dari logika pemilihan fungsi adalah:
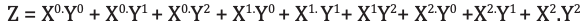
Analisis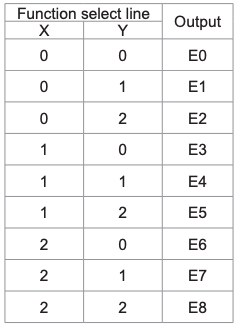
Demultiplexer juga disebut sebagai encoder. Fungsinya terbalik dengan multiplexer. Ia menerima input tunggal dan mendistribusikannya melalui beberapa output
Ternary d kait sederhana
Meskipun desain sirkuit yang menerapkan logika terner kombinasional sangat mudah, desain elemen memori ternary yang sederhana dan kuat (yaitu kait) yang cocok untuk implementasi sirkuit terintegrasi (IC) telah menjadi tantangan. Namun, kait terner sederhana dapat diperoleh dengan mengganti gerbang biner NOR atau NAND yang digunakan dengan gerbang T_NOR atau T_NAND.
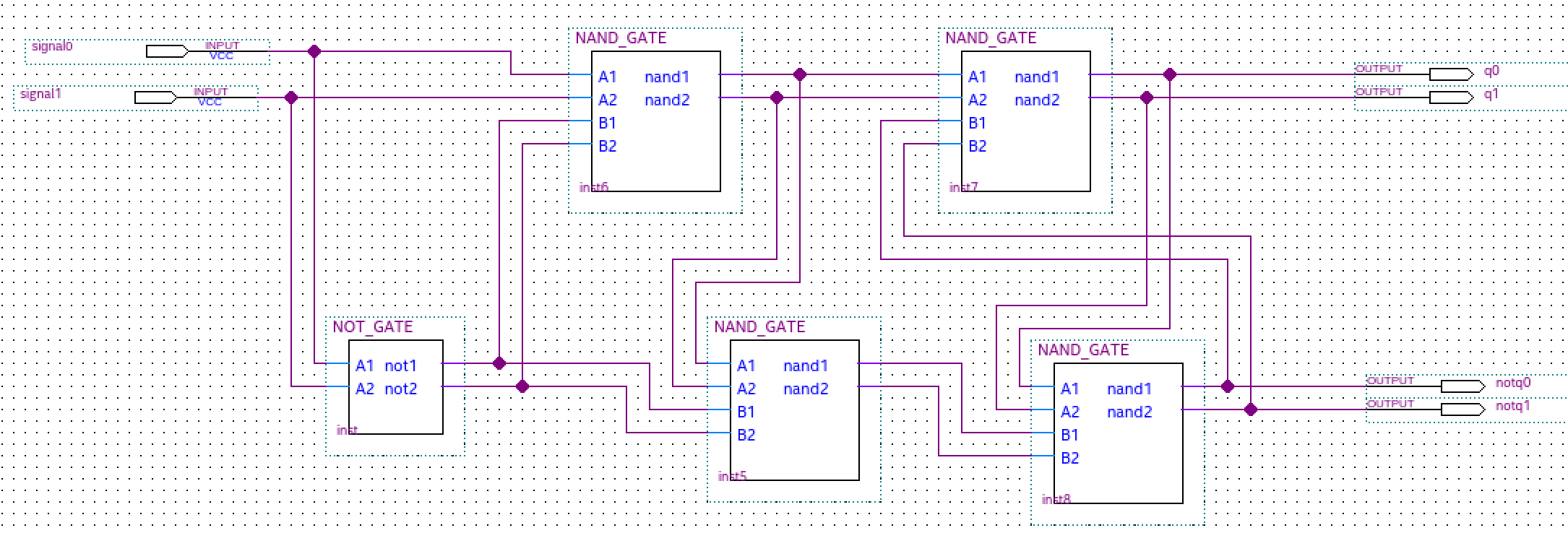
Sederhana Ternary D Flip-Flap-Flop
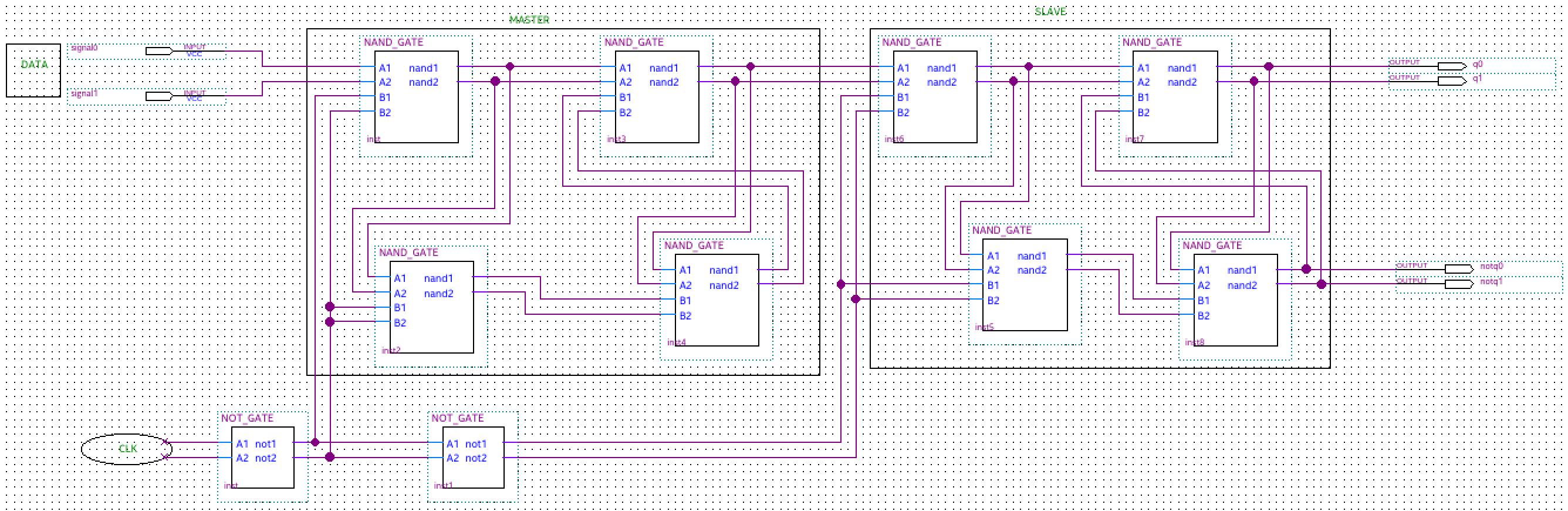
Master Slave (MS) ternary D Flip-Flap-Flop (FFF) direalisasikan berdasarkan pada kait D ternary. Ini mirip dengan cara biner D Flip-Flop (FF) direalisasikan menggunakan kait D biner. Diagram logika dan deskripsi operasi dari MS binary D flip-flop telah dikenal luas. Untuk mengimplementasikan MS ternary D FFF , kami mengganti kait D biner dengan kait D ternary (direalisasikan dengan gerbang negated-minimun gerbang dua input - NAND) dan pembalik biner dengan inverter ternary sederhana (IMS). Tabel kebenaran untuk sirkuit NAND ternary dan sirkuit STI ternary ditampilkan
Tabel kebenaran untuk sirkuit nand dan sti Untuk MS ternary D FFF dengan jam biner, datanya adalah ternary (logika 0, 1 dan 2) dan jam tersebut biner (rendah dan tinggi - di
implementasi, 0 dan 2 logika). MS ternary D FFF dengan
jam biner dapat membaca data saat jam beralih dari rendah ke
tinggi (tepi positif) atau dari tinggi ke rendah (tepi negatif), tergantung
pada jumlah IMS.
Input dari D FFF terner adalah Data dan Clk, dan outputnya adalah Q dan Not_Q. Sinyal clock adalah biner dan level logika dinotasikan 0 dan 2, untuk menjaga korespondensi dengan implementasi listrik
Unit Aritmatika dan Logika Ternary 1-bit (T-ALU)
Ternary Arithmetic Logic Unit (ALU) adalah sirkuit digital yang digunakan untuk melakukan operasi aritmatika dan logika. Ini merupakan blok bangunan mendasar dari Central Processing Unit (CPU) dari komputer ternary. ALU melakukan operasi aritmatika seperti operasi penambahan, pengurangan, perkalian, dan logika, NAND, NOR, NOT, AND, dan OR. Di bawah ini ditampilkan arsitektur primitif ALU 1 trit
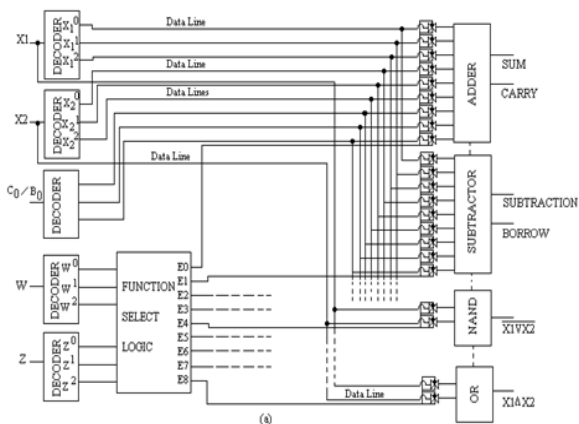
Tabel kebenaran dan berfungsi untuk T-ALU Blok bangunan dasar ALU adalah decoder, logika pilih fungsi (Multiplexer), gerbang transmisi dan modul pemrosesan terpisah. Logika pemilihan fungsi memilih 1 dari 9 fungsi yang terdaftar tergantung pada keadaan logika pada fungsi pilih garis W dan Z.
Jalur output dari logika pemilihan terhubung ke TG (gerbang Ternary) yang terkait dengan setiap modul. Modul apa pun dipilih hanya ketika TG terkait diaktifkan atau diisolasi dari jalur data. Untuk misalnya Jika input dari jalur pilih W dan Z = 0, output E 0 dari logika pemilihan tinggi (2) sedangkan E 1 , ke E 8 rendah (0) jadi, TG yang terkait dengan modul adder akan memungkinkan memungkinkan data
jalur yang akan dihubungkan ke modul adder sementara modul lain diisolasi dari jalur data.
Akhirnya, dengan cascading n / 2 trit, irisan ALU, ALU n trit dapat dibentuk.