Pendahuluan
Kami telah membuat kode Verilog yang dapat disintesis untuk menghitung akar kubus integer dari angka integer melalui algoritma pencarian biner. Kode ini telah diuji pada papan FPGA Cyclone IV. Di sini Anda dapat membaca tentang implementasi dan memahami cara kerja berbagai hal.
Tautan Github:
Root cubeApa itu root cube?
Root cube dari angka
y adalah angka
x sedemikian rupa
$$ tampilan $$ x ^ 3 = y tampilan $$ $$
Contoh:
$$ tampilkan $$ \ sqrt [3] {8} = 2 \\ \ sqrt [3] {27} = 3 \\ \ sqrt [3] {64} = 4 $$ tampilkan $$
Jadi, dalam implementasi kami, kami menggunakan
integer cube root .
Ini berarti bahwa akar pangkat tiga dari bilangan bulat
x adalah bilangan bulat lain sehingga:
$$ menampilkan $$ a ^ 3 \ leqslant x, \\ (a + 1) ^ 3 \ geqslant x $$ menampilkan $$
Contoh:
$$ menampilkan $$ \ sqrt [3] {26} = 2 \\ \ sqrt [3] {28} = 3 \\ \ sqrt [3] {63} = 3 \\ \ sqrt [3] {65} = 4 $$ menampilkan $$
Logika utama
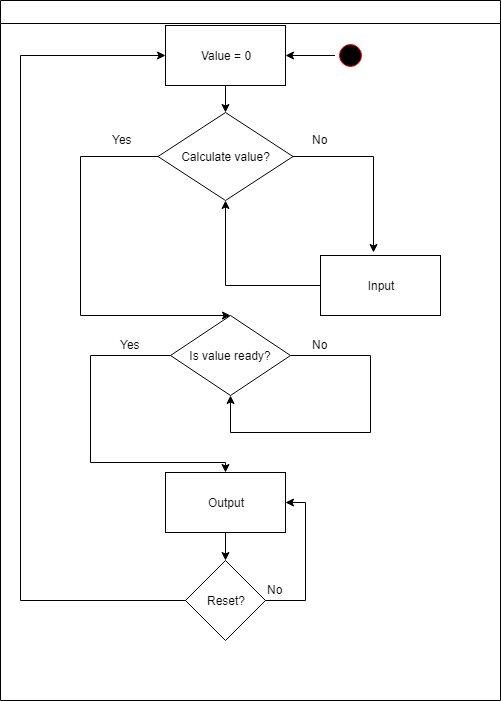
Modul utama bertanggung jawab untuk semua tindakan dengan angka selama input.
Ini memiliki 4 tindakan yang mungkin:
- kalikan selisih dengan 10
- bagi kenaikan dengan 10 (kenaikan selalu tidak kurang dari 1)
- menambah jumlah
- jumlah yang berkurang
Modul utamamodule cube_root( input inc, input sub, input next, input prev, input enter, input clk, output wire [7:0] leds, output wire [7:0] control ); reg signed [31:0] exit; wire ready; wire [31:0] res; reg zero = 0; // input // reg inc1 = 0; reg next1 = 0; reg prev1 = 0; reg sub1 = 0; reg enter1 = 0; reg [31:0] decimal = 1; ////////// reg [31:0] to_display; display_bcd display( .clk(clk), .value(ready == 0 ? exit : res), .control(control), .leds(leds) ); calculate calc( .clk(clk), .ready_to_calc(~enter), .num(exit), .ready(ready), .res(res) ); always @(posedge clk) begin if (enter == 1) begin if ((inc1 == 1'b0) && (~inc == 1'b1)) begin exit = exit + decimal; end inc1 = ~inc; if ((sub1 == 1'b0) && (~sub == 1'b1)) begin if (exit > 0) begin exit = exit - decimal; end end sub1 = ~sub; if ((next1 == 1'b0) && (~next == 1'b1)) begin decimal = decimal * 10; end next1 = ~next; if ((prev1 == 1'b0) && (~prev == 1'b1)) begin if (decimal >= 1 && decimal <= 9) begin decimal = 1; end else begin decimal = decimal / 10; end end prev1 = ~prev; end else begin if (ready == 1'b1) begin exit = 0; decimal = 1; end end end endmodule
Di modul utama
cube_root ada juga dua modul lain:
menghitung dan
display_bcd . Yang pertama melakukan semua perhitungan yang diperlukan, sedangkan modul kedua bertanggung jawab untuk menampilkan nilai input dan output selama eksekusi program.
Sekarang, mari kita pahami cara kerjanya.
Hitung modul
Modul perhitungan menggunakan algoritma pencarian biner. Dan ketika semua perhitungan dilakukan, ia menetapkan variabel
siap menjadi 1. Ini adalah sinyal untuk modul tampilan untuk menampilkan jawabannya.
Hitung modul module calculate( input clk, input ready_to_calc, input [31:0] num, output reg ready, output [31:0] res ); integer mid; integer start; integer final; integer counter; assign res = mid; always @(posedge clk) begin if (ready_to_calc == 1) begin if (ready == 0) begin mid = (start + final )/2; if ((mid*mid*mid) > num) begin final = mid; end else begin start = mid; end if (counter == 27) begin ready = 1; counter = 0; end else begin counter = counter + 1; end end end else begin final = 465; start = 0; ready = 0; counter = 0; end end endmodule
Mengapa modul ini melakukan 27 iterasi persis?- Nomor input maksimum adalah 99999999. Jadi, jumlah iterasi maksimum yang mungkin adalah
$ inline $ \ log_2 99999999 = 26.575424745 \ sekitar 27 $ inline $
Mengapa batas atas pencarian biner diinisialisasi oleh 465?- Karena itu angka maksimal yang bisa kita dapatkan sebagai hasilnya.
$ inline $ \ sqrt [3] {99999999} \ sekitar 464 $ inline $
Modul tampilan
Modul ini bertanggung jawab atas kinerja. Ia menggunakan delapan layar delapan segmen dan mereka dimanipulasi oleh 16 pin. Di mana 8 pin "bertanggung jawab" untuk led tertentu pada layar dan 8 pin lainnya adalah segmen kontrol, mereka mewakili angka yang berbeda.
Jadi, kami memberikan nilai integer yang ingin kami tampilkan ke modul ini. Kemudian, nilai ini diteruskan ke modul
Binary_to_BCD yang mengubah angka biner ke Binary Coded Decimal menggunakan
algoritma Double Dabble . Setelah itu, nilai yang dikonversi menjadi mudah ditampilkan.
Modul tampilan module display_bcd ( input clk, input [31:0] value, output [7:0] control, output [7:0] leds ); bcd_convert #(32, 8) bcd_convert( .i_Clock(clk), .i_Binary(value_temp), .i_Start(1'b1), .o_BCD(bcd_number), .o_DV(bcd_ready) ); integer delay = 0; integer final_bcd; reg [2:0] ctrl = 0; reg [4:0] digit; wire bcd_ready; wire [31:0] bcd_number; wire [31:0] digits; assign digits = final_bcd; wire [31:0] value_temp; assign value_temp = value; assign control = ~(1 << ctrl); assign leds = ~ (digit == 0 ? 8'b00111111 : (digit == 1 ? 8'b00000110 : (digit == 2 ? 8'b01011011 : (digit == 3 ? 8'b01001111 : (digit == 4 ? 8'b01100110 : (digit == 5 ? 8'b01101101 : (digit == 6 ? 8'b01111101 : (digit == 7 ? 8'b00000111 : (digit == 8 ? 8'b01111111 : (digit == 9 ? 8'b01101111 : 8'b00000000)))))))))); always @(posedge clk) begin if (bcd_ready) final_bcd = bcd_number; case(ctrl) 0: digit = digits[3:0]; 1: digit = digits[31:4] ? digits[7:4] : 10; 2: digit = digits[31:8] ? digits[11:8] : 10; 3: digit = digits[31:12] ? digits[15:12] : 10; 4: digit = digits[31:16] ? digits[19:16] : 10; 5: digit = digits[31:20] ? digits[23:20] : 10; 6: digit = digits[31:24] ? digits[27:24] : 10; 7: digit = digits[31:28] ? digits[31:28] : 10; endcase delay = delay + 1; if (delay == 10000) ctrl = ctrl + 1; end endmodule
Konversi Bcd module bcd_convert #(parameter INPUT_WIDTH, parameter DECIMAL_DIGITS) ( input i_Clock, input [INPUT_WIDTH-1:0] i_Binary, input i_Start, output [DECIMAL_DIGITS*4-1:0] o_BCD, output o_DV ); parameter s_IDLE = 3'b000; parameter s_SHIFT = 3'b001; parameter s_CHECK_SHIFT_INDEX = 3'b010; parameter s_ADD = 3'b011; parameter s_CHECK_DIGIT_INDEX = 3'b100; parameter s_BCD_DONE = 3'b101; reg [2:0] r_SM_Main = s_IDLE; // The vector that contains the output BCD reg [DECIMAL_DIGITS*4-1:0] r_BCD = 0; // The vector that contains the input binary value being shifted. reg [INPUT_WIDTH-1:0] r_Binary = 0; // Keeps track of which Decimal Digit we are indexing reg [DECIMAL_DIGITS-1:0] r_Digit_Index = 0; // Keeps track of which loop iteration we are on. // Number of loops performed = INPUT_WIDTH reg [7:0] r_Loop_Count = 0; wire [3:0] w_BCD_Digit; reg r_DV = 1'b0; always @(posedge i_Clock) begin case (r_SM_Main) // Stay in this state until i_Start comes along s_IDLE : begin r_DV <= 1'b0; if (i_Start == 1'b1) begin r_Binary <= i_Binary; r_SM_Main <= s_SHIFT; r_BCD <= 0; end else r_SM_Main <= s_IDLE; end // Always shift the BCD Vector until we have shifted all bits through // Shift the most significant bit of r_Binary into r_BCD lowest bit. s_SHIFT : begin r_BCD <= r_BCD << 1; r_BCD[0] <= r_Binary[INPUT_WIDTH-1]; r_Binary <= r_Binary << 1; r_SM_Main <= s_CHECK_SHIFT_INDEX; end // Check if we are done with shifting in r_Binary vector s_CHECK_SHIFT_INDEX : begin if (r_Loop_Count == INPUT_WIDTH-1) begin r_Loop_Count <= 0; r_SM_Main <= s_BCD_DONE; end else begin r_Loop_Count <= r_Loop_Count + 1; r_SM_Main <= s_ADD; end end // Break down each BCD Digit individually. Check them one-by-one to // see if they are greater than 4. If they are, increment by 3. // Put the result back into r_BCD Vector. s_ADD : begin if (w_BCD_Digit > 4) begin r_BCD[(r_Digit_Index*4)+:4] <= w_BCD_Digit + 3; end r_SM_Main <= s_CHECK_DIGIT_INDEX; end // Check if we are done incrementing all of the BCD Digits s_CHECK_DIGIT_INDEX : begin if (r_Digit_Index == DECIMAL_DIGITS-1) begin r_Digit_Index <= 0; r_SM_Main <= s_SHIFT; end else begin r_Digit_Index <= r_Digit_Index + 1; r_SM_Main <= s_ADD; end end s_BCD_DONE : begin r_DV <= 1'b1; r_SM_Main <= s_IDLE; end default : r_SM_Main <= s_IDLE; endcase end // always @ (posedge i_Clock) assign w_BCD_Digit = r_BCD[r_Digit_Index*4 +: 4]; assign o_BCD = r_BCD; assign o_DV = r_DV; endmodule // Binary_to_BCD
Penulis: Tyurin Leonid, Tikhonov Nikita.