Menggabungkan pekerjaan berdasarkan prinsip ini:

1. Subarrays yang dipesan dicari (sebagai opsi - dibentuk).
2. Subarrays yang dipesan digabung menjadi subarray yang umum dipesan.

Dengan sendirinya, setiap subarray yang dipesan di dalam array tidak memiliki banyak nilai. Tetapi jika dalam sebuah array kita menemukan dua sub-array yang dipesan, maka ini adalah masalah yang sama sekali berbeda. Faktanya adalah bahwa Anda dapat menggabungkan mereka dengan sangat cepat dan dengan biaya minimal - untuk membentuk subarray umum dari sepasang sub-array yang dipesan.



Seperti yang Anda lihat, menggabungkan dua array berurutan menjadi satu tidak mudah, tetapi sangat sederhana. Anda perlu bergerak secara bersamaan di kedua array dari kiri ke kanan dan membandingkan pasangan elemen berikutnya dari kedua array. Elemen yang lebih kecil dikirim ke boiler umum. Ketika elemen berakhir di salah satu array, elemen yang tersisa dari array lain hanya ditransfer ke daftar utama secara berurutan.

Ini adalah garam dari algoritma kelas ini. Awalnya, array acak dapat dibagi menjadi banyak subarrays kecil yang dipesan. Dalam penggabungan berpasangan, jumlah subarrays yang dipesan berkurang, panjang masing-masing sub-bertambah. Pada langkah terakhir, array hanya terdiri dari dua subarrays berurutan yang bergabung menjadi satu struktur berurutan.


Penulis konsep ini adalah John von Neumann. Kadang-kadang ada klaim kontroversial bahwa ia datang dengan menyortir saat bekerja di proyek Manhattan, karena ia dihadapkan dengan tugas memberikan perhitungan yang efektif dari sejumlah besar data statistik dalam pengembangan bom nuklir. Sulit untuk menilai kredibilitas versi ini, karena pekerjaan pertamanya pada penyortiran berdasarkan tanggal merger kembali ke 1948, dan pembuatan bom selesai 3 tahun sebelumnya. Namun, jenis penyortiran atom apa yang ada di sana, mari kita melihatnya.

Natural Neumann Fusion

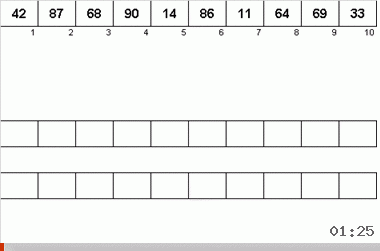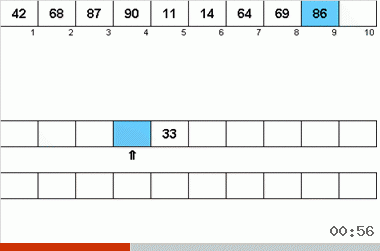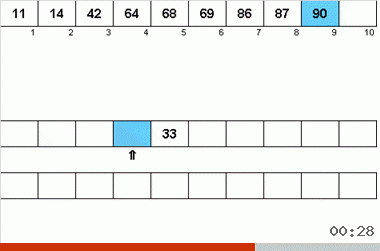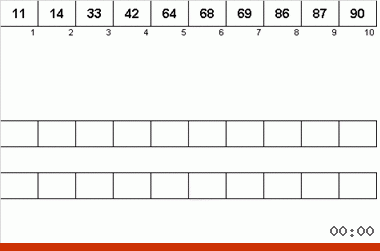
Algoritma Neyman dipengaruhi oleh fitur desain komputer tahun 40-an. Itu terlihat seperti ini:

1. Secara total, tiga pita magnetik digunakan - yang utama, di mana data yang tidak disortir dan dua data tambahan dicatat.
2. Data dibaca secara berurutan dari rekaman utama.
3. Sementara membaca data secara berurutan adalah subarray yang dipesan, mereka disalin ke salah satu kaset tambahan.
4. Segera setelah subarray yang diurutkan berikutnya selesai (mis., Elemen yang lebih kecil dari yang sebelumnya ditemukan pada pita utama), sebuah penunjuk ditempatkan pada pita bantu (ujung subarray) dan pergantian ke kaset tambahan terjadi.
5. Poin 2-4 diulangi lagi, hanya data yang ditransfer ke kaset tambahan lainnya. Pada akhir subarray yang dipesan berikutnya, pita utama secara bergantian beralih ke satu pita bantu, kemudian ke yang lain.
6. Ketika semua data dari rekaman utama telah dibaca, pemrosesan kaset tambahan dilakukan.
7. Kedua kaset tambahan membaca data secara bergantian.
8. Dalam hal ini, data selanjutnya dari dua kaset dibandingkan satu sama lain. Menurut hasil perbandingan, elemen terkecil dari pasangan dicatat pada kaset utama.
9. Karena batas-batas array pada kaset tambahan ditandai dengan pointer, pembacaan dan perbandingan hanya terjadi dalam sub-array yang diurutkan.
10. Jika pada salah satu kaset tambahan elemen dari subarray berikutnya selesai, maka dari kaset yang tersisa sisa dari subarray hanya ditransfer ke tape utama.
11. Kami ulangi seluruh proses lagi sampai data pada rekaman utama adalah susunan yang terurut sepenuhnya.

Penyortiran Neumann adalah suatu algoritma adaptif: ia tidak hanya memperbaiki potongan-potongan array yang diurutkan, tetapi juga pertama-tama mencoba untuk meningkatkannya, sehingga berdasarkan sub-susunan yang memanjang untuk membentuk sub-sus yang lebih panjang. Oleh karena itu, ini juga disebut penyortiran gabungan adaptif .

Kompleksitas algoritma ini sederhana - O ( n ² ), dan, bagaimanapun, untuk pelopor komputasi tabung ini merupakan terobosan.

Pada contoh jenis gabungan pertama ini, kelemahan dari kelas algoritma ini sudah terlihat - biaya memori tambahan. Dalam hal ini, hampir semua penyortiran gabungan juga membutuhkan O ( n ), namun, pengecualian elegan jarang terjadi.

Penggabungan langsung Bowes-Nelson

Sebenarnya, algoritma Bowes-Nelson adalah jaringan penyortiran, bukan penyortiran. Dalam prosesnya, array dan semua sub-layannya dibagi menjadi dua dan tidak ada yang mencegah semua bagian ini diproses secara paralel pada semua tahapan. Namun, itu juga bisa direpresentasikan dalam bentuk sortasi. Dan kita akan membahas topik menyortir jaringan juga.

1. Array dibagi menjadi dua - menjadi dua bagian kiri dan kanan.
2. Elemen dibagi menjadi kelompok-kelompok.
3. Pada iterasi pertama, ini adalah dua elemen (elemen pertama setengah kiri + elemen pertama setengah kanan, elemen kedua setengah kiri + elemen kedua setengah kanan, dll.), Pada iterasi kedua - empat elemen (1- Elemen ke-2 dan ke-2 dari setengah kiri + elemen ke-1 dan ke-2 dari setengah ke kanan, ke-3 dan ke-4 elemen dari ke-setengah + ke-3 dan ke-4 dari elemen di sebelah kanan, dll.), Di ketiga - delapan, dll.
4. Elemen-elemen dari masing-masing kelompok dari bagian kiri adalah sub-susunan yang diurutkan, elemen-elemen dari setiap kelompok dari bagian-bagian kanan juga sub-susunan yang diurutkan.
5. Gabungkan subarrays yang diurutkan dari paragraf sebelumnya.
6. Kami kembali ke titik 1. Siklus berlanjut hingga ukuran grup lebih kecil dari ukuran array.

Sepertinya memori tambahan diperlukan di sini. Tapi tidak! Untuk persepsi yang lebih dimengerti dalam animasi, bagian kiri dan kanan array terletak satu sama lain, sehingga posisi relatif dari subarrays yang dibandingkan lebih jelas. Namun, karena pembelahan yang ketat, suatu algoritma dimungkinkan di mana semua perbandingan dan pertukaran dilakukan, tanpa melibatkan sumber daya tambahan dari memori. Yang sangat tidak biasa untuk menyortir gabungan.

def bose_nelson(data): m = 1 while m < len(data): j = 0 while j + m < len(data): bose_nelson_merge(j, m, m) j = j + m + m m = m + m return data def bose_nelson_merge(j, r, m): if j + r < len(data): if m == 1: if data[j] > data[j + r]: data[j], data[j + r] = data[j + r], data[j] else: m = m // 2 bose_nelson_merge(j, r, m) if j + r + m < len(data): bose_nelson_merge(j + m, r, m) bose_nelson_merge(j + m, r - m, m) return data 

Ada sesuatu dalam semua jenis merger yang membuatnya mirip dengan bom hidrogen. Pembelahan pertama terjadi, kemudian sintesis.

Referensi

Gabung / Gabung

Artikel Seri:

• Aplikasi Excel AlgoLab.xlsm
• Pertukaran macam
• Urutan Penyisipan
• Sortir berdasarkan pilihan
• Gabungkan Urusan
  • Merger top-down dan bottom-up yang seimbang
  • Sortasi Penggabungan Multi-fase
  • Cascading Merge Sort
  • Urutkan Gabung Berosilasi
  • Penyortiran berulir dan tidak bercampur
  • Gabungkan Sortir Perbandingan
• Urutkan berdasarkan distribusi
• Sortasi Hibrid

Kedua penyortiran yang disebutkan dalam artikel hari ini sekarang tersedia di aplikasi AlgoLab (bagi mereka yang mempelajari algoritma menggunakan aplikasi Excel ini, perbarui file). Dan hanya dalam beberapa hari, dengan rilis tindak lanjut segera pada jenis penggabungan, beberapa algoritma lainnya dari kelas ini akan tersedia.

Ada batasan untuk penyortiran Bowes-Nelson - ukuran array harus memiliki kekuatan dua. Jika kondisi ini tidak terpenuhi, maka makro akan memotong array ke ukuran yang sesuai.

Artikel ini ditulis dengan dukungan EDISON Software, sebuah perusahaan yang menulis perangkat lunak rekonstruksi 3D dan sedang mengembangkan peralatan pengukuran yang canggih .