Setelah booming nyata permainan papan di akhir tahun 00-an, keluarga meninggalkan beberapa kotak dengan permainan. Salah satunya adalah game "Hare and Hedgehog" dalam versi asli Jerman. Sebuah permainan untuk beberapa pemain, di mana unsur keacakan diminimalkan, dan perhitungan yang bijaksana dan kemampuan pemain untuk "melihat ke depan" dengan beberapa langkah menang.
Kekalahan saya yang sering terjadi dalam permainan membuat saya menulis "kecerdasan" komputer untuk memilih langkah terbaik. Kecerdasan, idealnya mampu melawan grandmaster Hare dan Hedgehog (dan apa, teh, bukan catur, permainan akan lebih mudah). Sisa artikel ini menjelaskan proses pengembangan, logika AI, dan tautan ke sumber.
Aturan permainan Hare dan Hedgehog
Di lapangan bermain 65 sel ada beberapa chip pemain, dari 2 hingga 6 peserta (gambar saya, non-kanonik, penampilan, tentu saja, biasa saja):
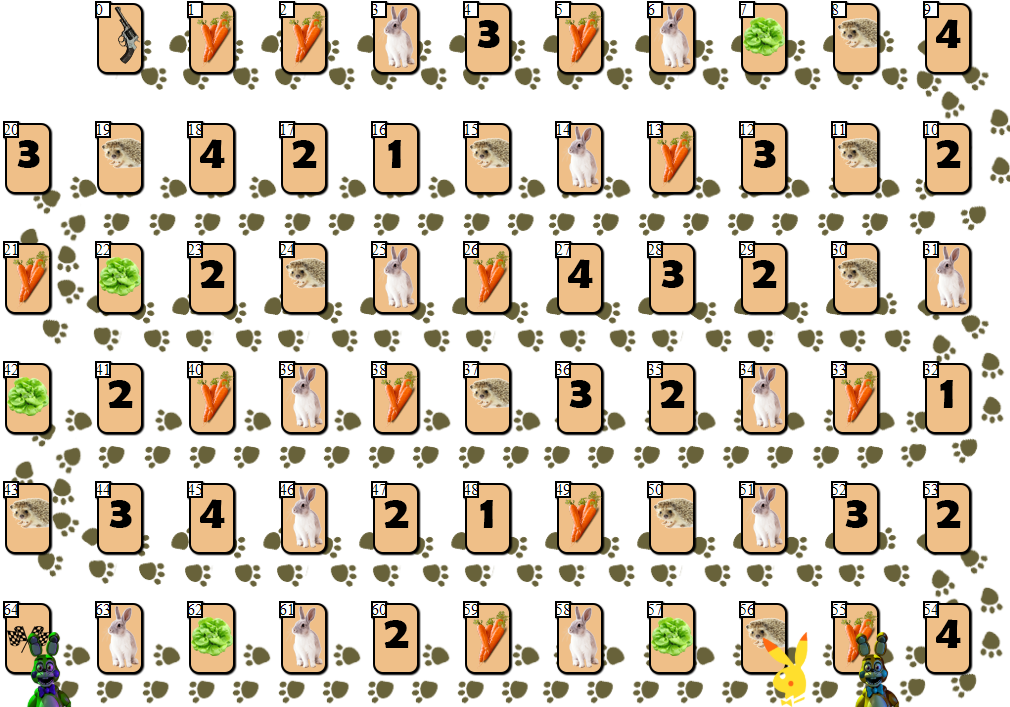
Terlepas dari sel dengan indeks 0 (mulai) dan 64 (selesai), hanya satu pemain dapat ditempatkan di masing-masing sel. Tujuan setiap pemain adalah bergerak maju ke sel finish, di depan para pesaing.
"Bahan bakar" untuk bergerak maju adalah wortel - "
mata uang " permainan. Pada awalnya, setiap pemain menerima 68 wortel, yang ia berikan (dan kadang-kadang menerima) saat ia bergerak.
Selain wortel, pada awalnya pemain menerima 3 kartu salad. Salad adalah "artefak" khusus yang harus
disingkirkan seorang pemain sebelum selesai. Menyingkirkan selada (dan ini hanya bisa dilakukan pada selada khusus, seperti ini:

), pemain, termasuk, menerima wortel tambahan. Sebelum itu, lewati langkah Anda. Semakin banyak pemain di depan salad yang meninggalkan kartu, semakin banyak wortel yang akan diterima pemain: 10 x (posisi pemain di lapangan relatif terhadap pemain lain). Artinya, pemain yang berdiri di atas lapangan kedua akan menerima 20 wortel, meninggalkan sangkar salad.
Sel dengan angka 1 - 4 dapat membawa beberapa puluh wortel jika posisi pemain bertepatan dengan angka pada sel (1 - 4, sel dengan nomor 1 juga cocok untuk posisi ke-4 dan ke-6 di lapangan), dengan analogi dengan sel selada.
Pemain dapat melewatkan langkah, tetap di kandang dengan gambar wortel dan menerima atau memberikan 10 wortel untuk tindakan ini. Mengapa pemain harus memberi "bahan bakar"? Faktanya adalah bahwa seorang pemain dapat menyelesaikan hanya memiliki 10 wortel setelah langkah terakhirnya (20 jika Anda finis kedua, 30 jika Anda finis ketiga, dll.).
Akhirnya, pemain bisa mendapatkan 10 x N wortel dengan mengambil langkah N di landak
gratis terdekat (jika landak terdekat sibuk, langkah seperti itu tidak mungkin).
Biaya bergerak maju dihitung tidak proporsional dengan jumlah gerakan, sesuai dengan rumus (dengan pembulatan ke atas):
,
di mana N adalah jumlah langkah maju.
Jadi untuk melangkah maju satu sel, pemain memberikan 1 wortel, 3 wortel untuk 2 sel, 6 wortel untuk 3 sel, 10 untuk 4, ..., 210 wortel untuk memindahkan 20 sel ke depan.
Sel terakhir - sel dengan gambar kelinci - memperkenalkan unsur keacakan ke dalam permainan. Setelah berdiri di kandang dengan kelinci, pemain mengambil kartu khusus dari tumpukan, setelah itu beberapa tindakan dilakukan. Bergantung pada kartu dan situasi permainan, pemain dapat kehilangan beberapa wortel, mendapatkan wortel ekstra atau melewatkan satu putaran. Perlu dicatat bahwa di antara kartu dengan "efek" ada beberapa skenario negatif bagi pemain, yang mendorong permainan untuk berhati-hati dan dihitung.
Implementasi tanpa AI
Dalam implementasi pertama, yang kemudian akan menjadi dasar untuk pengembangan "kecerdasan" gaming, saya membatasi diri pada opsi di mana setiap pemain membuat gerakan - seseorang.
Saya memutuskan untuk mengimplementasikan game sebagai klien - situs web satu halaman statis, semua "logika" yang diimplementasikan pada JS dan server - aplikasi WEB API. Server ditulis dalam .NET Core 2.1 dan menghasilkan satu artefak perakitan - file dll, yang dapat dijalankan di bawah Windows / Linux / Mac OS.
"Logika" dari bagian klien diminimalkan (serta UX, karena GUI adalah murni utilitarian). Misalnya, klien web tidak melakukan pemeriksaan sendiri untuk melihat apakah aturan yang diminta oleh pemain dapat diterima. Pemeriksaan ini dilakukan di server. Server memberi tahu klien tentang gerakan apa yang dapat dilakukan pemain dari posisi permainan saat ini.
Server adalah
mesin Moore klasik. Logika server tidak memiliki konsep seperti "klien yang terhubung", "sesi permainan", dll.
Yang dilakukan server hanyalah memproses perintah yang diterima (HTTP POST). Pola
"perintah" diterapkan di server. Klien dapat meminta eksekusi salah satu dari perintah berikut:
- memulai permainan baru, mis. "Tempatkan" chip dari jumlah pemain yang ditentukan di papan "bersih"
- lakukan langkah yang ditunjukkan dalam perintah
Untuk tim kedua, klien mengirimkan server posisi permainan saat ini (objek dari kelas Disposisi), yaitu, deskripsi bentuk berikut:
- posisi, jumlah wortel, dan selada untuk masing-masing kelinci, ditambah bidang Boolean tambahan yang menunjukkan bahwa kelinci tersebut kehilangan gilirannya
- indeks kelinci membuat langkah.
Server tidak perlu mengirim informasi tambahan - misalnya, informasi tentang lapangan permainan. Sama seperti untuk merekam sketsa catur, Anda tidak perlu mengecat susunan sel hitam dan putih di papan tulis - informasi ini diambil sebagai konstanta.
Sebagai tanggapan, server menunjukkan apakah perintah berhasil diselesaikan. Secara teknis, klien dapat, misalnya, meminta langkah yang tidak valid. Atau coba buat game baru untuk satu peserta, yang jelas tidak masuk akal.
Jika tim berhasil, respons akan berisi
posisi permainan baru, serta daftar gerakan yang dapat dilakukan oleh pemain berikutnya dalam antrian (saat ini untuk posisi baru).
Selain itu, respons server berisi beberapa bidang layanan. Misalnya, teks kartu seekor kelinci “ditarik keluar” oleh pemain pada langkah di kandang yang sesuai.
Putar Pemain
Giliran pemain dikodekan sebagai bilangan bulat:
- 0, jika pemain dipaksa untuk tetap di sel saat ini,
1, 2, ... N untuk 1, ... N melangkah maju, - -1, -2, ... -M untuk memindahkan 1 ... sel M kembali ke landak gratis terdekat,
- 1001, 1002 - kode khusus untuk pemain yang memutuskan untuk tetap di sel wortel dan menerima (1001) atau memberikan (1002) 10 wortel untuk itu.
Implementasi perangkat lunak
Server menerima JSON dari perintah yang diminta, mem-parsingnya ke dalam salah satu kelas permintaan yang sesuai, dan melakukan tindakan yang diminta.
Jika klien (pemain) diminta untuk bergerak dengan kode CMD dari posisi (POS) yang ditransfer ke tim, server melakukan tindakan berikut:
- memeriksa apakah langkah seperti itu mungkin dilakukan
- menciptakan posisi baru dari yang sekarang, menerapkan modifikasi yang sesuai dengannya,
mendapat banyak kemungkinan gerakan untuk posisi baru. Biarkan saya mengingatkan Anda bahwa indeks pemain yang bergerak sudah termasuk dalam objek yang menggambarkan posisi , - mengembalikan kepada klien jawaban dengan posisi baru, kemungkinan gerakan atau tanda sukses sama dengan false, dan deskripsi kesalahan.
Logika mengecek diterimanya langkah yang diminta (CMD) dan membangun posisi baru ternyata sedikit lebih dekat terhubung daripada yang kita inginkan. Dengan logika ini, metode untuk menemukan gerakan yang dapat diterima memiliki kesamaan. Semua fungsi ini diimplementasikan oleh kelas TurnChecker.
Pada input metode pemeriksaan / eksekusi, TurnChecker menerima objek dari kelas posisi permainan (Disposisi). Objek Disposisi berisi larik data pemain (Haze [] hazes), indeks pemain yang bergerak + beberapa informasi layanan yang diisi selama pengoperasian objek TurnChecker.
Lapangan bermain menggambarkan kelas FieldMap, yang diimplementasikan sebagai
singleton . Kelas berisi array sel + beberapa informasi overhead yang digunakan untuk menyederhanakan / mempercepat perhitungan selanjutnya.
Pertimbangan KinerjaDalam implementasi kelas TurnChecker, saya mencoba untuk menghindari loop sebanyak mungkin. Faktanya adalah bahwa metode untuk memperoleh seperangkat gerakan yang diizinkan / eksekusi langkah selanjutnya akan disebut ribuan (puluhan ribu) kali selama prosedur pencarian untuk langkah kuasi-optimal.
Jadi, misalnya, saya menghitung berapa banyak sel yang pemain dapat maju dengan N wortel, menggunakan rumus:
return ((int)Math.Pow(8 * N + 1, 0.5) - 1) / 2;
Memeriksa apakah sel saya ditempati oleh salah satu pemain, saya tidak melihat daftar pemain (karena tindakan ini mungkin harus dilakukan berkali-kali), tetapi saya beralih ke kamus formulir
[cell_index, busy_cage_ flag] yang diisi terlebih dahulu.
Saat memeriksa apakah sel landak yang ditentukan adalah yang terdekat (di belakang) dengan sel saat ini yang ditempati oleh pemain, saya juga membandingkan posisi yang diminta dengan nilai dari kamus formulir
[cell_index, terdekat_back_dezh] _index] - informasi statis.
Implementasi dengan AI
Satu perintah ditambahkan ke daftar perintah yang diproses oleh server: jalankan langkah kuasi-optimal yang dipilih oleh program. Tim ini adalah modifikasi kecil dari perintah "gerakan pemain", yang darinya, bidang gerakan (
CMD ) telah dihapus.
Keputusan pertama yang muncul dalam pikiran adalah menggunakan heuristik untuk memilih langkah "terbaik". Dengan analogi dengan catur, kita dapat mengevaluasi setiap posisi permainan yang diperoleh dengan langkah kita dengan menetapkan semacam peringkat untuk posisi ini.
Evaluasi posisi heuristik
Sebagai contoh, dalam catur, untuk membuat penilaian (tanpa merangkak ke dalam belantara bukaan) cukup sederhana: minimal, Anda dapat menghitung total "biaya" dari potongan-potongan dengan mengambil nilai ksatria / uskup untuk 3 pion, nilai rook menjadi 5 pion, ratu ke 9, dan raja untuk
int .MaxValue pion. Mudah untuk meningkatkan taksiran, misalnya, menambahnya (dengan faktor koreksi - faktor / eksponen atau fungsi lainnya):
- jumlah kemungkinan gerakan dari posisi saat ini,
- rasio ancaman terhadap angka musuh / ancaman dari musuh.
Penilaian khusus diberikan pada posisi mat:
int.MaxValue , jika skakmat menempatkan komputer,
int.MinValue jika skakmat menempatkan orang tersebut.
Jika Anda memesan prosesor catur untuk memilih langkah berikutnya, hanya dipandu oleh penilaian seperti itu, prosesor mungkin akan memilih bukan gerakan terburuk. Khususnya:
- Jangan lewatkan kesempatan untuk mengambil bagian yang lebih besar atau skakmat,
- kemungkinan besar, itu tidak akan mendorong angka-angka di sudut-sudut,
- Itu tidak membuat angka diserang lagi (mengingat jumlah ancaman dalam penilaian).
Tentu saja, gerakan komputer seperti itu tidak akan memberinya peluang sukses dengan lawan yang membuat gerakannya dalam arti sekecil apa pun. Komputer akan mengabaikan salah satu colokan. Selain itu, dia mungkin tidak ragu untuk menukar ratu dengan pion.
Namun demikian, algoritma untuk evaluasi heuristik dari posisi bermain saat ini dalam catur (tanpa mengklaim kemenangan program juara) cukup transparan. Anda tidak bisa mengatakan tentang game Hare dan Hedgehog.
Dalam kasus umum, dalam game the Hare and the Hedgehog, pepatah yang agak kabur bekerja: "
lebih baik melangkah lebih jauh dengan lebih banyak wortel dan lebih sedikit selada " Namun, tidak semuanya begitu mudah. Katakanlah, jika seorang pemain memiliki 1 kartu salad di tengah permainan, opsi ini bisa sangat bagus. Tetapi pemain yang berdiri di garis finish dengan kartu salad jelas akan berada dalam situasi kalah. Selain algoritma evaluasi, saya juga ingin dapat "mengintip" selangkah lebih maju, sama seperti ancaman terhadap potongan dapat dihitung dalam evaluasi heuristik dari posisi catur. Sebagai contoh, ada baiknya mempertimbangkan bonus wortel yang diterima oleh pemain yang meninggalkan sel sel / posisi sel (1 ... 4), dengan mempertimbangkan jumlah pemain di depan.
Saya menyimpulkan nilai akhir sebagai fungsi:
E = Ks * S + Kc * C + Kp * P,
di mana S, C, P adalah nilai yang dihitung menggunakan kartu salad (S) dan wortel © di tangan pemain, P adalah nilai yang diberikan kepada pemain untuk jarak yang ditempuh.
Ks, Kc, Kp adalah faktor koreksi yang sesuai (mereka akan dibahas nanti).
Cara termudah adalah saya menentukan tanda untuk
jalur yang dilalui :
P = i * 3, di mana i adalah indeks sel tempat pemain berada.
Grading C (wortel) sudah lebih sulit.
Untuk mendapatkan nilai C tertentu, saya memilih satu dari 3 fungsi
dari satu argumen (jumlah wortel di tangan). Indeks fungsi C ([0, 1, 2]) ditentukan oleh posisi relatif pemain di lapangan bermain:
- [0] jika pemain telah menyelesaikan kurang dari setengah lapangan bermain,
- [2] jika seorang pemain memiliki cukup (mb, bahkan banyak) wortel untuk diselesaikan,
- [1] dalam kasus lain.
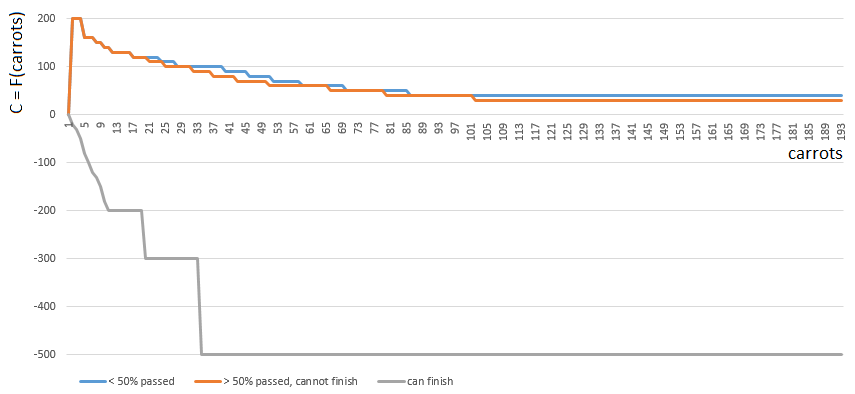
Fungsi 0 dan 1 serupa: “nilai” setiap wortel di tangan pemain secara bertahap berkurang dengan meningkatnya jumlah wortel di tangan. Gim ini jarang mendorong Plyushkins. Dalam kasus 1 (setengah dari bidang berlalu), nilai wortel berkurang sedikit lebih cepat.
Fungsi 2 (pemain dapat menyelesaikan), sebaliknya, mengenakan denda besar (nilai koefisien negatif) pada setiap wortel di tangan pemain - semakin banyak wortel, semakin besar koefisien penalti. Karena dengan kelebihan wortel, hasil akhir dilarang oleh aturan permainan.
Sebelum menghitung jumlah wortel di tangan pemain ditentukan dengan memperhitungkan wortel per langkah dari sel sel / nomor 1 ... 4.
"
Selada " kelas S disimpulkan dengan cara yang sama. Bergantung pada jumlah salad di tangan pemain (0 ... 3), fungsi dipilih
atau
. Argumen fungsi
. - lagi, jalur "relatif" yang dilalui oleh pemain. Yaitu, jumlah sel dengan salad yang tersisa di depan (relatif terhadap sel yang ditempati oleh pemain):
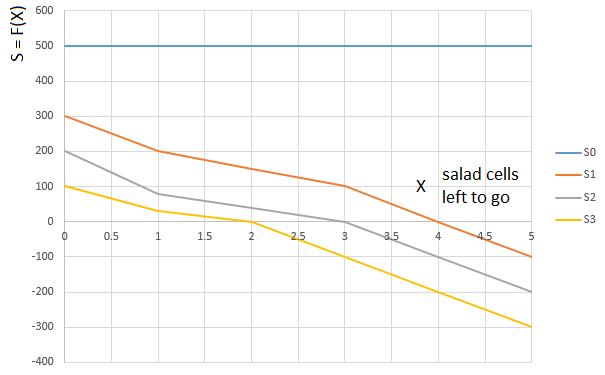
Kurva
- fungsi evaluasi (S) pada jumlah sel selada di depan pemain (0 ... 5), untuk pemain dengan 0 kartu selada di tangan,
kurva
- fungsi yang sama untuk pemain dengan satu kartu salad, dll.
Nilai akhir (E = Ks * S + Kc * C + Kp * P) dengan demikian memperhitungkan:
- jumlah tambahan wortel yang akan diterima pemain segera sebelum kepindahannya sendiri,
- jalur pemain
- jumlah wortel dan selada di tangan yang mempengaruhi skor secara nonlinier.
Dan inilah cara komputer bermain, memilih langkah selanjutnya dengan skor heuristik maksimum:
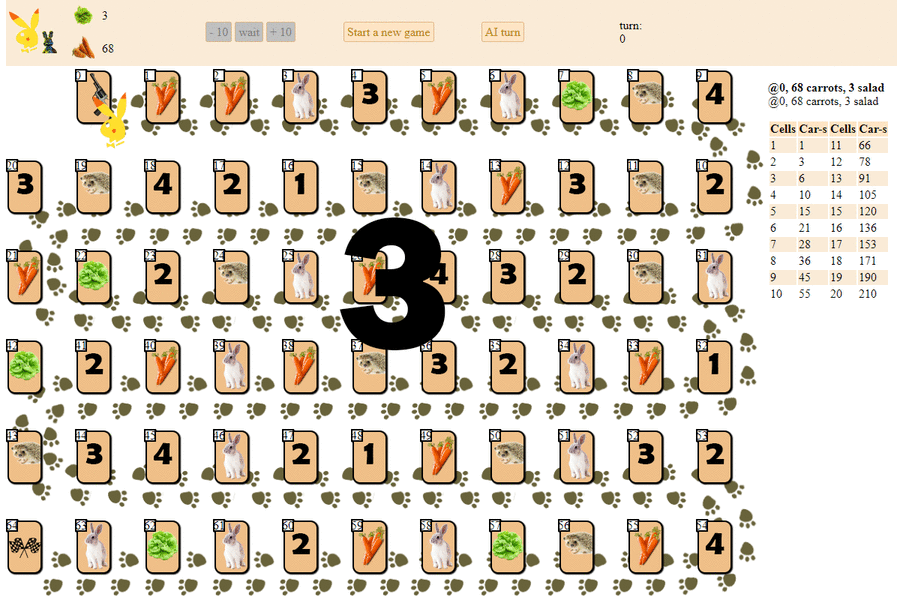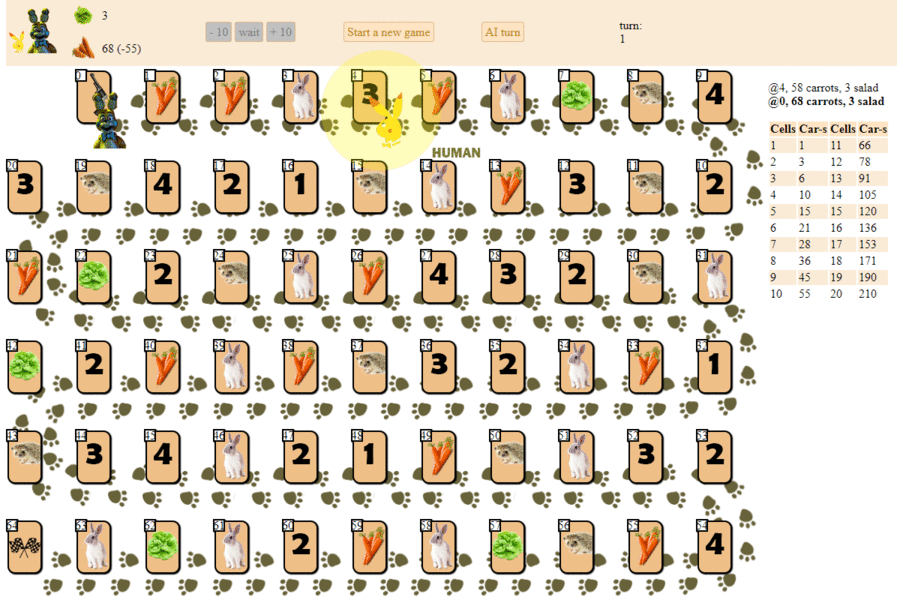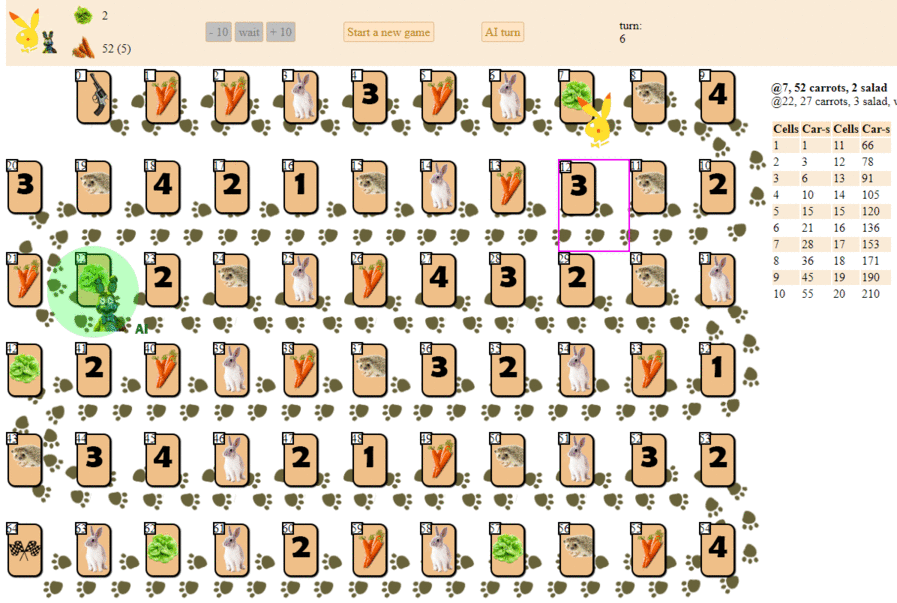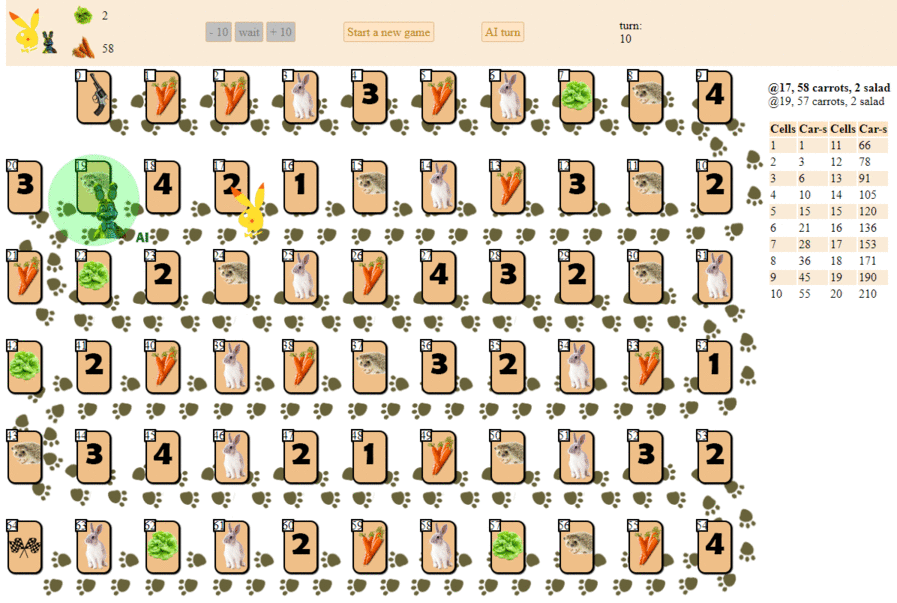
Pada prinsipnya, debutnya tidak terlalu buruk. Namun, kita seharusnya tidak mengharapkan game yang bagus dari AI seperti itu: di tengah permainan, "robot" hijau mulai membuat gerakan berulang, dan pada akhirnya membuat beberapa iterasi bergerak maju - mundur ke landak, sampai akhirnya selesai. Sebagian karena kebetulan, ia akan finis di belakang pemain - seseorang dengan selusin gerakan.
Catatan ImplementasiPerhitungan penilaian dikelola oleh kelas khusus - EstimationCalculator. Fungsi untuk mengevaluasi posisi relatif terhadap kartu salad wortel dimuat ke dalam array di konstruktor statis dari kelas kalkulator. Metode estimasi posisi menerima objek posisi itu sendiri dan indeks pemain, dari "sudut pandang" yang posisinya dievaluasi oleh algoritma. Artinya, posisi permainan yang sama dapat menerima beberapa peringkat berbeda, tergantung pada pemain mana poin virtual dipertimbangkan.
Decision Tree dan Algoritma Minimax
Kami menggunakan algoritma pengambilan keputusan dalam game Minimax yang antagonis. Sangat bagus, menurut saya, algoritma ini dijelaskan dalam
posting ini (terjemahan) .
Kami mengajarkan program untuk "melihat" beberapa langkah ke depan. Misalkan, dari posisi saat ini (dan latar belakang tidak penting untuk algoritma - seperti yang kita ingat, program berfungsi sebagai
mesin Moore ), diberi nomor dengan angka 1, program dapat membuat dua gerakan. Kami mendapatkan dua posisi yang memungkinkan, 2 dan 3. Selanjutnya adalah giliran pemain - orang (dalam kasus umum - musuh). Dari posisi 2, lawan memiliki 3 gerakan, dari yang ketiga - hanya dua gerakan. Selanjutnya, giliran untuk bergerak kembali ke program, yang, secara total, dapat membuat 10 gerakan dari 5 posisi yang memungkinkan:
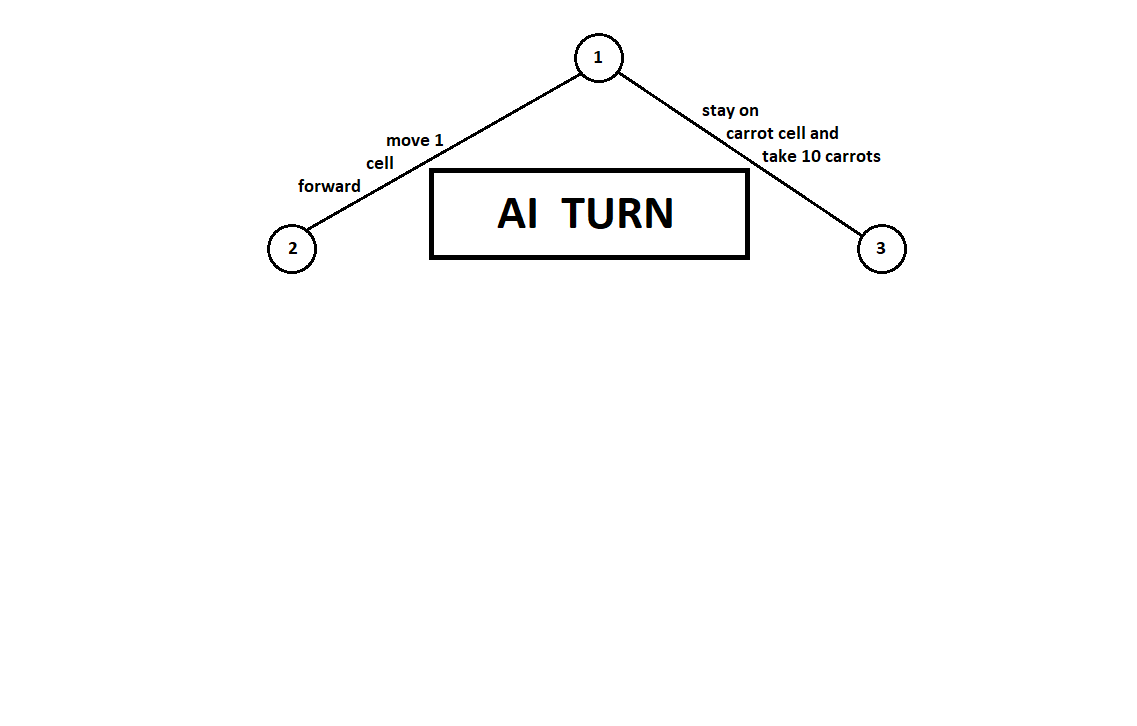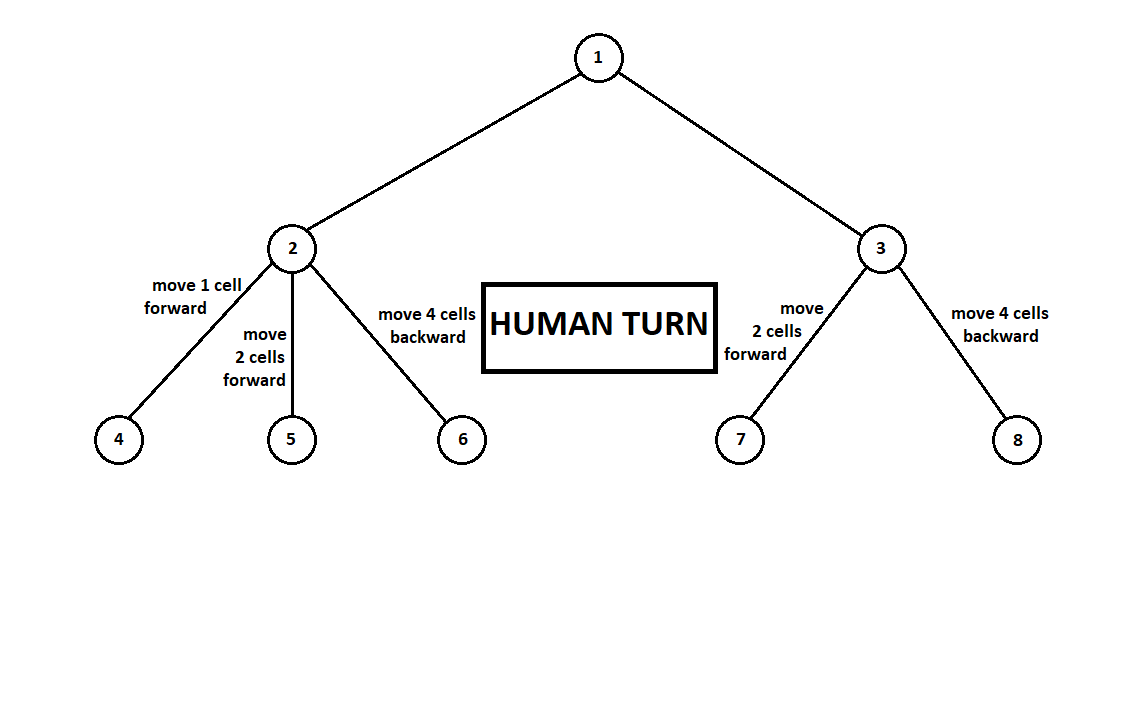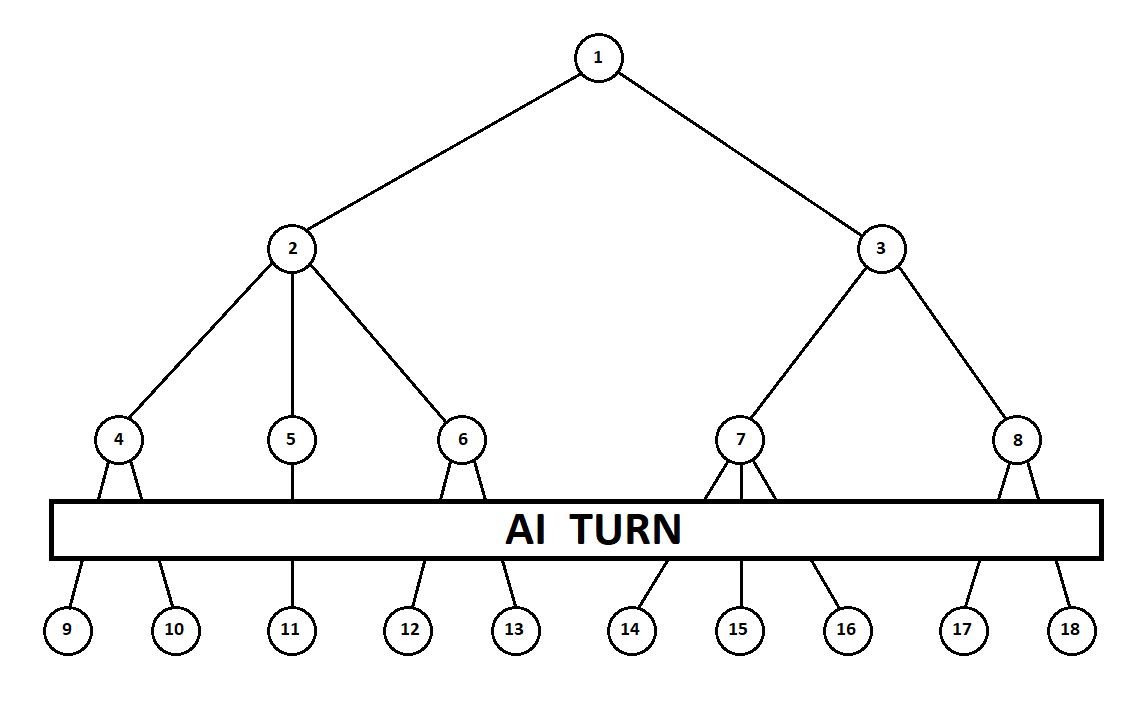
Misalkan, setelah langkah kedua komputer, permainan berakhir dan masing-masing posisi yang diterima dievaluasi dari sudut pandang pemain pertama dan kedua. Dan kami sudah menerapkan algoritma evaluasi. Mari kita evaluasi setiap posisi akhir (daun pohon 9 ... 18) dalam bentuk vektor
,
dimana
- skor dihitung untuk pemain pertama,
- skor pemain kedua:
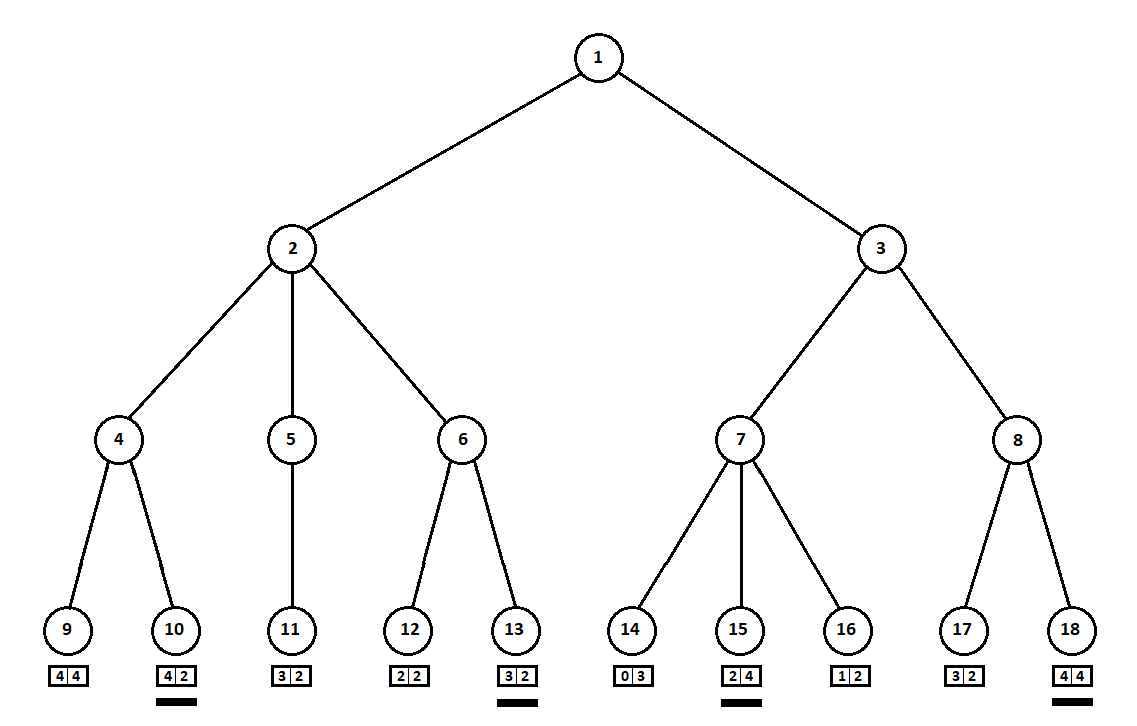
Karena komputer membuat langkah terakhir, itu jelas akan memilih opsi di masing-masing sub pohon ([9, 10], [11], [12, 13], [14, 15, 16], [17, 18]) yang memberinya peringkat yang lebih baik. Pertanyaan segera muncul: dengan prinsip apa seseorang harus memilih posisi "terbaik"?
Misalnya, ada dua gerakan, setelah itu kami memiliki posisi dengan peringkat [5; 5] dan [2; 1]. Mengevaluasi pemain pertama. Dua alternatif sudah jelas:
- pemilihan posisi dengan nilai absolut maksimum dari skor ke-i untuk pemain ke-i. Dengan kata lain, pembalap mulia Leslie, ingin sekali menang, tanpa memperhatikan pesaing. Dalam hal ini, posisi dengan perkiraan [5; 5].
- pilihan posisi dengan peringkat maksimum relatif terhadap perkiraan pesaing adalah profesor Iman yang licik, yang tidak melewatkan kesempatan untuk memberikan trik kotor pada musuh. Misalnya, sengaja ketinggalan perencanaan pemain untuk memulai dari posisi kedua. Item dengan peringkat [2; 1].
Dalam implementasi perangkat lunak saya, saya membuat algoritme pemilihan tingkat (fungsi yang memetakan vektor tingkat ke nilai skalar untuk pemain ith) sebagai parameter khusus. Tes lebih lanjut menunjukkan, yang mengejutkan saya, keunggulan strategi pertama - pilihan posisi dengan nilai absolut maksimum
.
Fitur implementasi perangkat lunakJika opsi pertama untuk memilih kelas terbaik ditentukan dalam pengaturan AI (kelas TurnMaker), kode metode yang sesuai akan berbentuk:
int ContractEstimateByAbsMax(int[] estimationVector, int playerIndex) { return estimationVector[playerIndex]; }
Metode kedua - relatif relatif terhadap posisi pesaing - diterapkan sedikit lebih rumit:
int ContractEstimateByRelativeNumber(int[]eVector, int player) { int? min = null; var pVal = eVector[player]; for (var i = 0; i < eVector.Length; i++) { if (i == player) continue; var val = pVal - eVector[i]; if (!min.HasValue || min.Value > val) min = val; } return min.Value; }
Estimasi yang dipilih (digarisbawahi dalam gambar) ditransfer ke tingkat atas. Sekarang musuh harus memilih posisi, mengetahui posisi selanjutnya yang akan dipilih algoritma:
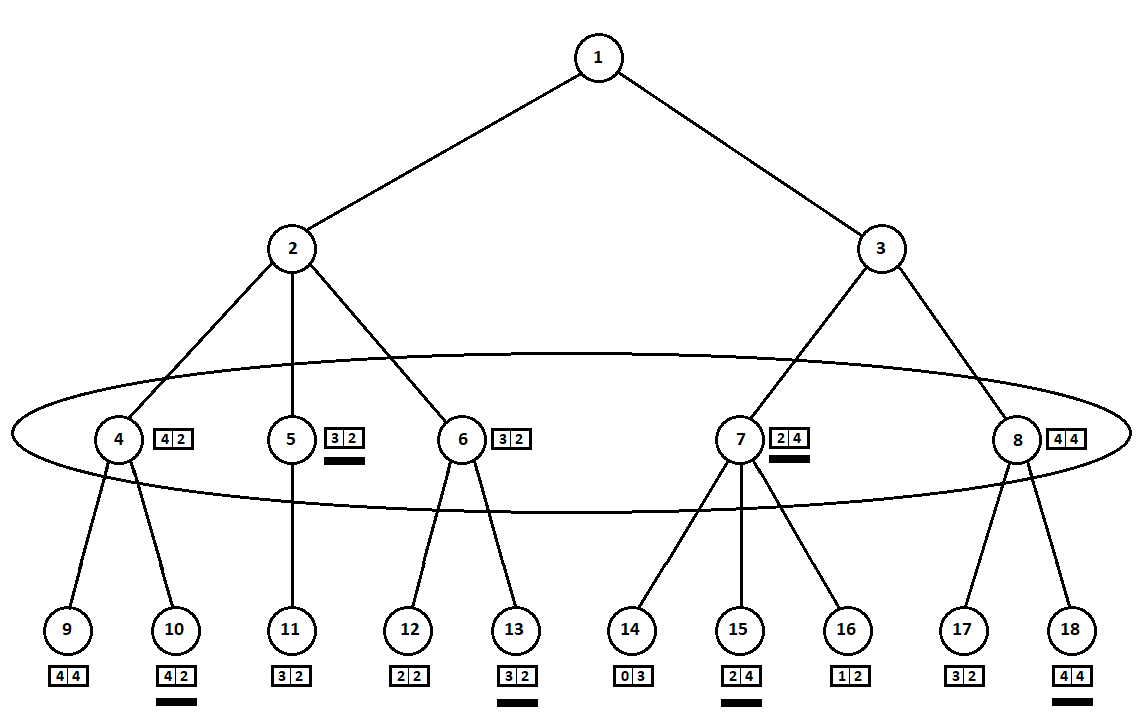
Musuh, tentu saja, akan memilih posisi dengan peringkat terbaik untuk dirinya sendiri (yang mana
koordinat kedua vektor mengambil nilai terbesar). Perkiraan ini sekali lagi digarisbawahi dalam grafik.
Akhirnya, kami kembali ke langkah pertama. Komputer memilih, dan dia lebih suka bergerak dengan koordinat pertama terbesar dari vektor:
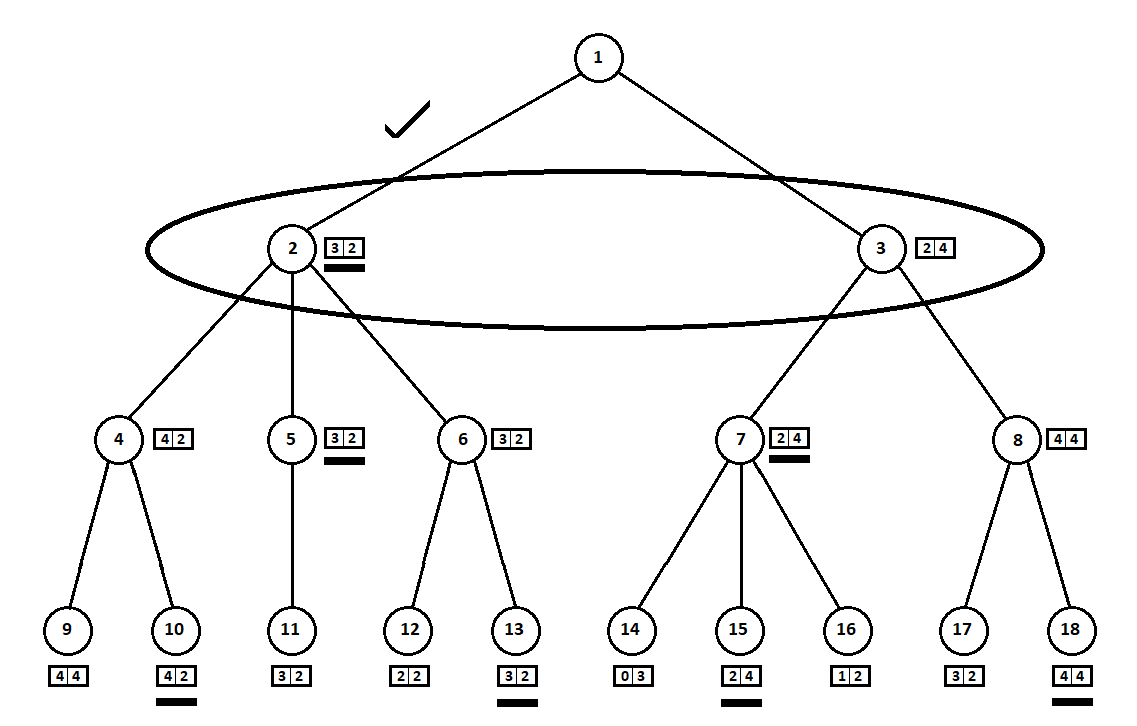
Dengan demikian, masalah terpecahkan - langkah kuasi-optimal ditemukan. Misalkan skor heuristik 100% pada posisi daun pada pohon menunjukkan pemenang di masa depan. Maka algoritma kami akan dengan tegas memilih langkah terbaik yang mungkin.
Namun, skor heuristik adalah 100% akurat hanya ketika posisi
akhir permainan dievaluasi - satu (atau beberapa) pemain telah selesai, pemenang ditentukan. Oleh karena itu, memiliki kesempatan untuk melihat ke depan gerakan N - sebanyak yang diperlukan untuk memenangkan saingan dengan kekuatan yang sama, Anda dapat memilih langkah yang optimal.
Tapi permainan tipikal untuk 2 pemain berlangsung rata-rata sekitar 30 - 40 gerakan (untuk tiga pemain - sekitar 60 gerakan, dll.). Dari setiap posisi, seorang pemain biasanya dapat membuat sekitar 8 gerakan. Akibatnya, pohon lengkap posisi yang memungkinkan untuk 30 gerakan akan terdiri dari sekitar
= 1237940039285380274899124224 puncak!
Dalam praktiknya, membangun dan "mem-parsing" pohon dengan ~ 100.000 posisi pada PC saya membutuhkan waktu sekitar 300 milidetik. Yang memberi kita batas pada kedalaman pohon di level 7 - 8 (bergerak), jika kita ingin mengharapkan respons komputer tidak lebih dari satu detik.
Fitur implementasi perangkat lunakJelas, metode rekursif diperlukan untuk membangun pohon posisi dan menemukan langkah terbaik. Pada input metode - posisi saat ini (di mana, seperti yang kita ingat, pemain sudah bergerak) dan level pohon saat ini (nomor langkah). Segera setelah kami turun ke level maksimum yang diizinkan oleh pengaturan algoritma, fungsi mengembalikan vektor estimasi posisi heuristik dari "sudut pandang" masing-masing pemain.
Tambahan penting : keturunan di bawah pohon juga harus dihentikan ketika pemain saat ini selesai. Kalau tidak (jika algoritma untuk memilih posisi terbaik relatif terhadap posisi pemain lain dipilih), program dapat "menginjak" di finish untuk waktu yang lama, "mengejek" lawan. Selain itu, dengan cara ini kita akan sedikit mengurangi ukuran pohon di endgame.
Jika kita belum berada pada level rekursi tertinggi, maka kita memilih gerakan yang mungkin, buat posisi baru untuk setiap gerakan dan meneruskannya ke panggilan rekursif dari metode saat ini.
Mengapa Minimax?Dalam interpretasi asli para pemain selalu dua. Program ini menghitung skor secara eksklusif dari posisi pemain pertama. Dengan demikian, ketika memilih posisi "terbaik", pemain dengan indeks 0 mencari posisi dengan peringkat maksimum, pemain dengan indeks 1 mencari minimum.
Dalam kasus kami, peringkat harus berupa vektor sehingga masing-masing pemain N dapat mengevaluasinya dari "sudut pandang", karena peringkat naik ke pohon.
Tuning AI
Praktek saya bermain melawan komputer telah menunjukkan bahwa algoritma tidak begitu buruk, tetapi masih kalah dengan manusia. Saya memutuskan untuk meningkatkan AI dalam dua cara:
- mengoptimalkan konstruksi / traversal dari pohon keputusan,
- meningkatkan heuristik.
Optimasi algoritma Minimax
Pada contoh di atas, kita dapat menolak untuk mempertimbangkan posisi 8 dan “menyimpan” 2 - 3 simpul pohon:
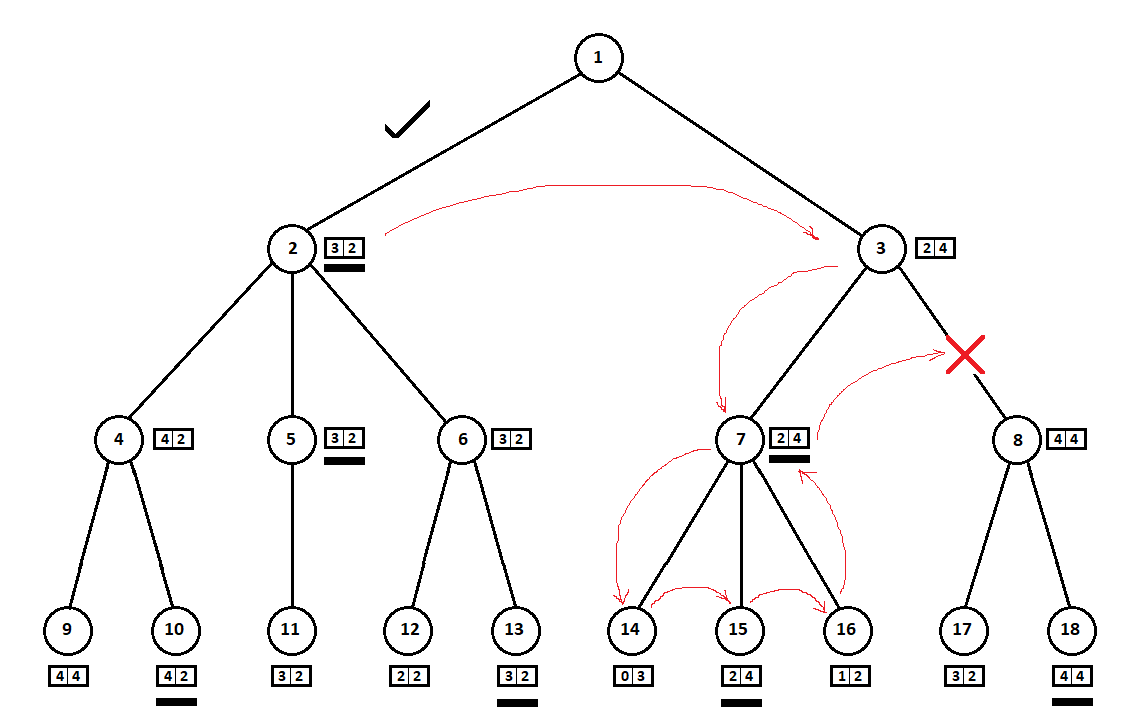
Kami berjalan di sekitar pohon dari atas ke bawah, dari kiri ke kanan. Melewati subtree mulai dari posisi 2, kami menyimpulkan perkiraan terbaik untuk langkah 1 -> 2: [3, 2]. Memotong subtree dengan root di posisi 7, kami menentukan peringkat saat ini (terbaik untuk bergerak 3 -> 7): [2, 4]. Dari sudut pandang komputer (pemain pertama), skor [2, 4] lebih buruk daripada skor [3, 2]. Dan karena lawan komputer memilih langkah dari posisi 3, berapa pun skor untuk posisi 8, skor akhir untuk posisi 3 akan lebih buruk daripada skor yang diperoleh untuk posisi ketiga. Dengan demikian, subtree dengan root di posisi 8 tidak dapat dibangun dan tidak dievaluasi.
Versi optimal dari algoritma Minimax, yang memungkinkan Anda untuk memotong sub-sub pohon berlebih, disebut
algoritma kliping alpha-beta . Menerapkan algoritma ini akan memerlukan modifikasi kecil pada kode sumber.
Fitur implementasi perangkat lunakDua parameter integer juga diteruskan ke metode CalcEstimate dari kelas TurnMaker - alpha, yang sama dengan int.MinValue awalnya dan beta, yaitu int.MaxValue. Lebih lanjut, setelah menerima estimasi pergerakan saat ini dalam pertimbangan, pseudocode dari form dieksekusi:
e = _[0]
Fitur penting dari implementasi perangkat lunakmetode kliping alpha-beta, menurut definisi, mengarah ke solusi yang sama dengan algoritma Minimax "bersih". Untuk memeriksa apakah logika pengambilan keputusan telah berubah (atau lebih tepatnya, hasilnya bergerak), saya menulis tes unit di mana robot membuat 8 gerakan untuk masing-masing 2 lawan (total 16 gerakan) dan menyimpan serangkaian gerakan yang dihasilkan - dengan opsi kliping dinonaktifkan .
Kemudian, dalam tes yang sama, prosedur diulangi dengan opsi kliping dihidupkan . Setelah itu, urutan gerakan dibandingkan. Perbedaan dalam gerakan menunjukkan kesalahan dalam implementasi algoritma kliping alpha-beta (tes gagal).
Optimalisasi kliping alpha-beta kecil
Dengan opsi kliping diaktifkan di pengaturan AI, jumlah simpul di pohon posisi berkurang rata-rata 3 kali. Hasil ini bisa agak ditingkatkan.
Dalam contoh di atas:

begitu berhasil "bertepatan" sehingga, sebelum subtree dengan vertex di posisi 3, kami memeriksa subtree dengan vertex di posisi 2. Jika urutannya berbeda, kita bisa mulai dengan subtree "terburuk" dan tidak menyimpulkan bahwa tidak ada gunanya mempertimbangkan posisi berikutnya. .
Sebagai aturan, kliping pada pohon ternyata lebih “ekonomis”, simpul turunannya pada level yang sama (yaitu, semua kemungkinan pergerakan dari posisi-i) sudah diurutkan berdasarkan estimasi posisi saat ini (tanpa melihat ke dalam). Dengan kata lain, kami menganggap bahwa langkah terbaik (dari sudut pandang heuristik) lebih mungkin untuk mendapatkan nilai akhir yang lebih baik. Jadi, kami, dengan beberapa kemungkinan, mengurutkan pohon sehingga subtree "terbaik" akan dipertimbangkan sebelum yang "terburuk", yang akan memungkinkan kami untuk memotong lebih banyak opsi.
Penilaian posisi saat ini adalah prosedur yang mahal. Jika sebelumnya cukup bagi kita untuk mengevaluasi hanya posisi terminal (daun), maka sekarang penilaian dibuat untuk semua simpul pohon. Namun, seperti yang ditunjukkan oleh tes, jumlah perkiraan yang dibuat masih sedikit kurang dari dalam versi tanpa penyortiran awal dari kemungkinan langkah.
Fitur implementasi perangkat lunakAlgoritme kliping alpha-beta mengembalikan langkah yang sama dengan algoritma Minimax asli. Ini memeriksa unit test yang kami tulis, membandingkan dua urutan gerakan (untuk algoritma dengan kliping dan tanpa). Pemangkasan alfa-beta dengan penyortiran , dalam kasus umum, dapat mengindikasikan perpindahan berbeda sebagai kuasi-optimal.
Untuk menguji operasi yang benar dari algoritma yang dimodifikasi, Anda perlu tes baru. Meskipun ada modifikasi, algoritma dengan pengurutan harus menghasilkan vektor estimasi akhir yang persis sama ([3, 2] pada contoh pada gambar) sebagai algoritma tanpa pengurutan seperti algoritma Minimax asli.
Dalam pengujian, saya membuat serangkaian posisi uji dan memilih dari masing-masing sesuai dengan gerakan "terbaik", menghidupkan dan mematikan opsi pengurutan. Kemudian ia membandingkan vektor evaluasi yang diperoleh dengan dua cara.
Selain itu, karena posisi untuk masing-masing gerakan yang mungkin dalam simpul pohon saat ini diurutkan berdasarkan evaluasi heuristik, itu memunculkan ide untuk segera membuang beberapa opsi terburuk. Sebagai contoh, seorang pemain catur dapat mempertimbangkan gerakan di mana ia mengganti bentengnya untuk pukulan gadai. Namun, dengan "membuka gulungan" situasi secara mendalam dengan 3, 4 ... maju bergerak, ia akan segera melihat opsi ketika, misalnya, lawan menempatkan uskup ratu diserang.
Dalam pengaturan AI, saya mengatur vektor "kliping opsi terburuk". Misalnya, vektor formulir [0, 0, 8, 8, 4] berarti bahwa:
- melihat satu [0] dan dua [0] langkah maju, program akan mempertimbangkan semua kemungkinan langkah, karena 0 ,
- [8] [8] , 8 “” , , ,
- melihat lima atau lebih langkah ke depan [4], program ini akan mengevaluasi tidak lebih dari 4 gerakan "terbaik".
Dengan penyortiran diaktifkan untuk algoritma kliping alfa-beta dan vektor yang serupa dalam pengaturan kliping, program mulai menghabiskan sekitar 300 milidetik untuk memilih langkah semu-optimal, “melangkah lebih dalam” 8 langkah maju.Optimalisasi Heuristik
Terlepas dari jumlah posisi vertex yang layak yang diulang di pohon dan "dalam" memandang ke depan untuk mencari langkah kuasi-optimal, AI memiliki beberapa kelemahan. Saya mendefinisikan salah satu dari mereka sebagai " perangkap kelinci ".Perangkap kelinci. ( 8 — 10 15), . “” ( !):
. :
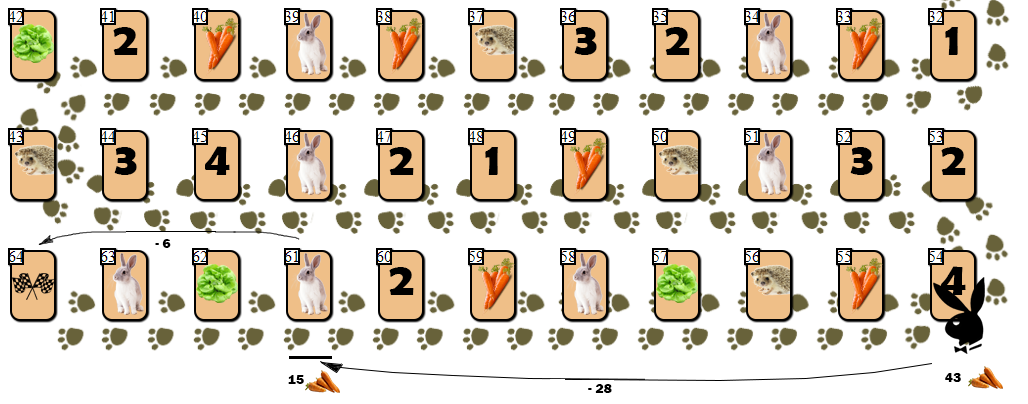
54 (43), — 10 55 . AI, , (61), 28 . , 6 9 ( 10 ).
, ( ), , 4 — 6 . , , , AI ?
,
, . AI . , , . “ ” :
65 — “” , , . , , , () .
Faktor Koreksi
Sebelumnya, memberikan rumus untuk estimasi heuristik dari posisi saat iniE = Ks * S + Kc * C + Kp * P,saya sebutkan, tetapi tidak menjelaskan, faktor koreksi.Faktanya adalah bahwa rumus itu sendiri dan set fungsi 45;26;2;f;29;19;0;f;2 ...
Baris ini secara harfiah berarti yang berikut:- pemain pertama berada di kotak 45, ia memiliki 26 kartu wortel dan 2 kartu salad di tangannya, pemain tidak ketinggalan langkah (f = false). Hak untuk bergerak selalu menjadi pemain pertama.
- pemain kedua pada sel 29 dengan 19 kartu wortel dan tanpa kartu salad, tidak ketinggalan bergerak.
- angka dua berarti bahwa, "memutuskan" studi, saya berasumsi bahwa pemain kedua berada dalam situasi kemenangan.
Setelah memasukkan 20 sketsa ke dalam program, saya “mengunduhnya” di game web-client, dan kemudian mengurutkan masing-masing sketsa. Menganalisis sketsa, saya bergantian membuat gerakan untuk masing-masing pemain, sampai saya memutuskan "pemenang". Setelah menyelesaikan penilaian, saya mengirimkannya dalam tim khusus ke server.Setelah mengevaluasi 20 etudes (tentu saja, akan bermanfaat untuk menganalisis lebih banyak dari mereka), saya mengevaluasi masing-masing etudes oleh program. Dalam evaluasi, nilai masing-masing faktor koreksi, dari 0,5 menjadi 2 dalam peningkatan 0,1 - totalRingkasan
Akibatnya, saya mendapatkan program yang berfungsi, yang, sebagai aturan, mengalahkan saya dalam versi satu-satu terhadap komputer. Statistik kemenangan dan kekalahan yang serius untuk versi program saat ini belum diakumulasikan. Mungkin penyetelan AI mudah berikutnya akan membuat kemenangan saya tidak mungkin. Atau hampir mustahil, karena faktor sel kelinci masih tetap ada.Misalnya, dalam logika memilih peringkat (maksimum absolut atau relatif relatif terhadap pemain lain), saya pasti akan mencoba opsi perantara. Paling tidak, jika nilai absolut dari skor pemain ith adalah sama, masuk akal untuk memilih langkah yang mengarah ke posisi dengan nilai relatif yang lebih besar dari skor (gabungan dari bangsawan Leslie dan Feith yang berbahaya).Program ini berfungsi penuh untuk versi dengan 3 pemain. Namun, ada kecurigaan bahwa “kualitas” pergerakan AI untuk bermain dengan 3 pemain lebih rendah daripada untuk bermain dengan dua pemain. Namun, selama tes terakhir saya kehilangan komputer - mungkin karena kelalaian, dengan santai mengevaluasi jumlah wortel di tangan saya dan datang ke garis finish dengan kelebihan "bahan bakar".Sejauh ini, pengembangan lebih lanjut dari AI terhambat oleh kurangnya seseorang - "tester", yaitu, lawan hidup dari "jenius" komputer. Saya sendiri memainkan cukup banyak Hare dan Hedgehog untuk mual dan dipaksa untuk mengganggu pada tahap saat ini.→ Tautan ke repositori dengan sumber