Matematika di Gamedev sederhana. Matriks dan transformasi affine

Halo semuanya! Nama saya Grisha dan saya adalah pendiri CGDevs. Hari ini saya ingin melanjutkan topik matematika di game dev. Dalam artikel sebelumnya , kami menunjukkan contoh dasar menggunakan vektor dan integral dalam proyek Unity, dan sekarang mari kita bicara tentang matriks dan transformasi affine. Jika Anda berpengalaman dalam aritmatika matriks; Anda tahu apa itu TRS dan bagaimana cara mengatasinya; apa itu transformasi Householder - Anda mungkin tidak akan menemukan sesuatu yang baru untuk diri Anda sendiri. Kami akan berbicara dalam konteks grafik 3D. Jika Anda tertarik dengan topik ini - selamat datang di kucing.



Mari kita mulai dengan salah satu konsep terpenting dalam konteks artikel - transformasi affine . Transformasi affine pada dasarnya adalah transformasi sistem koordinat (atau ruang) dengan mengalikan vektor dengan matriks khusus. Misalnya, transformasi seperti gerakan, rotasi, penskalaan, refleksi, dll. Sifat utama dari transformasi affine adalah Anda tetap berada di ruang yang sama (tidak mungkin membuat vektor dua dimensi dari dua dimensi) dan bahwa jika garis berpotongan / berparalel Saya dilintasi sebelum konversi, maka properti ini akan dipertahankan setelah konversi. Selain itu, mereka memiliki banyak sifat matematika yang membutuhkan pengetahuan tentang teori kelompok, set dan aljabar linier, yang membuat bekerja dengan mereka lebih mudah.

Matriks TRS

Konsep penting kedua dalam grafik komputer adalah matriks TRS . Dengan menggunakannya, Anda dapat menggambarkan operasi yang paling umum digunakan saat bekerja dengan grafik komputer. Matriks TRS adalah komposisi dari tiga matriks transformasi. Matriks perpindahan (Terjemahan), rotasi pada setiap sumbu (Rotasi) dan penskalaan (Skala).
Dia terlihat seperti ini.



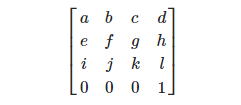
Dimana:
Langkahnya adalah t = Vector3 baru (d, h, l).
Penskalaan - s = Vector3 baru (Vector3 baru (a, e, i) .magnitude, Vector3 baru (b, f, j) .magnitude, Vector3 baru (c, g, k) .magnitude);

Rotasi adalah matriks bentuk:



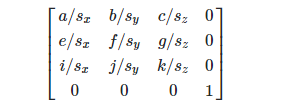
Sekarang mari kita masuk lebih dalam ke konteks Unity. Untuk mulai dengan, matriks TRS adalah hal yang sangat nyaman, tetapi tidak boleh digunakan di mana-mana. Karena indikasi sederhana dari posisi atau penambahan vektor dalam suatu unit akan bekerja lebih cepat, tetapi dalam banyak algoritma matematika, matriks jauh lebih mudah daripada vektor. Fungsionalitas TRS di Unity sebagian besar diimplementasikan di kelas Matrix4x4 , tetapi tidak nyaman dari sudut pandang aplikasi. Karena, selain menerapkan matriks melalui perkalian, ia umumnya dapat menyimpan informasi tentang orientasi objek, dan untuk beberapa transformasi, saya ingin dapat menghitung tidak hanya posisi, tetapi juga mengubah orientasi objek secara keseluruhan (misalnya, refleksi yang tidak diterapkan dalam Unity)

Semua contoh diberikan di bawah ini untuk sistem koordinat lokal (asal GameObject dianggap sebagai asal koordinat, di mana objek berada. Jika objek adalah akar hierarki dalam unit, maka asal adalah dunia (0,0,0)).

Karena menggunakan matriks TRS pada dasarnya kita dapat menggambarkan posisi suatu objek dalam ruang, kita memerlukan dekomposisi dari TRS ke nilai spesifik posisi, rotasi dan skala untuk Unity. Untuk melakukan ini, Anda bisa menulis metode ekstensi untuk kelas Matrix4x4


Selain itu, untuk pekerjaan yang mudah, Anda dapat menerapkan beberapa ekstensi kelas Transform untuk bekerja dengan TRS di dalamnya.


Mengenai hal ini, keuntungan dari persatuan berakhir, karena matriks dalam Persatuan sangat buruk dalam operasinya. Banyak algoritma membutuhkan aritmatika matriks, yang tidak diimplementasikan dalam unit bahkan dalam operasi yang sepenuhnya dasar, seperti menambahkan matriks dan mengalikan matriks dengan skalar. Selain itu, karena kekhasan implementasi vektor di Unity3d, ada juga beberapa ketidaknyamanan terkait dengan fakta bahwa Anda dapat membuat vektor 4x4, tetapi tidak dapat membuat 1x4 di luar kotak. Karena kita akan berbicara lebih banyak tentang transformasi Householder untuk refleksi, pertama-tama kita mengimplementasikan operasi yang diperlukan untuk ini.

Menambahkan / mengurangi dan mengalikan dengan skalar sederhana. Ini terlihat agak besar, tetapi tidak ada yang rumit di sini, karena aritmatika sederhana.


Tetapi untuk refleksi, kita membutuhkan operasi perkalian matriks dalam kasus khusus tertentu. Penggandaan vektor dimensi 4x4 oleh 1x4 (ditranskripsikan) Jika Anda terbiasa dengan matematika matriks, maka Anda tahu bahwa dengan penggandaan ini Anda perlu melihat angka ekstrim dari dimensi, dan Anda akan mendapatkan dimensi matriks pada output, yaitu, dalam hal ini 4x4. Ada informasi yang cukup tentang bagaimana matriks dikalikan, jadi kami tidak akan melukis ini. Berikut adalah contoh kasus tertentu yang akan berguna di masa depan.

Transformasi Householder

Dalam mencari cara untuk mencerminkan objek relatif terhadap sumbu apa pun, saya sering menemukan saran untuk menempatkan skala negatif ke arah yang diperlukan. Ini adalah saran yang sangat buruk dalam konteks Unity, karena ia memecah banyak sistem dalam mesin (batching, collision, dll.) Dalam beberapa algoritma, ini berubah menjadi perhitungan yang sangat tidak sepele jika Anda perlu mencerminkan tidak sepele sehubungan dengan Vector3.up atau Vector3.forward, tetapi dalam arah yang sewenang-wenang. Metode refleksi dalam unit out of the box itu sendiri tidak diterapkan, jadi saya menerapkan metode Householder .

Transformasi Householder digunakan tidak hanya dalam grafik komputer, tetapi dalam konteks ini adalah transformasi linear yang mencerminkan objek relatif terhadap pesawat yang melewati "asal" dan ditentukan oleh normal ke pesawat. Dalam banyak sumber, ini dijelaskan dengan cukup rumit dan tidak dapat dipahami, walaupun formulanya sederhana.

H = I-2 * n * (n ^ T)

Di mana H adalah matriks transformasi, I dalam kasus kami adalah Matrix4x4.identity, dan n = Vector4 baru (planeNormal.x, planeNormal.y, planeNormal.z, 0). Simbol T berarti transposisi, yaitu, setelah mengalikan n * (n ^ T) kita mendapatkan matriks 4x4.

Metode yang diimplementasikan akan berguna dan rekaman akan sangat kompak.


Penting: planeNormal harus dinormalisasi (yang logis), dan koordinat terakhir n harus 0, sehingga tidak ada efek peregangan arah, karena itu tergantung pada panjang vektor n.

Sekarang untuk kenyamanan di Unity, kami menerapkan metode ekstensi untuk transformasi


Itu saja untuk hari ini, jika seri artikel ini akan terus menarik, saya juga akan mengungkapkan aplikasi matematika lainnya dalam pengembangan game. Kali ini tidak akan ada proyek, karena semua kode ditempatkan di artikel, tetapi proyek dengan aplikasi spesifik akan ada di artikel berikutnya. Dari gambar ini Anda bisa menebak apa artikel selanjutnya.



Terima kasih atas perhatian anda!