Butuh Kabur Lebih Berbeda

Pengaburan gambar dengan filter Gaussian Blur banyak digunakan dalam berbagai tugas. Tetapi kadang-kadang Anda ingin sedikit lebih banyak variasi daripada hanya satu filter untuk semua kesempatan, di mana hanya satu parameter cocok untuk penyesuaian - ukurannya. Pada artikel ini, kita akan melihat beberapa implementasi blur lainnya.

Pendahuluan

Efek Gaussian Blur adalah operasi linier dan secara matematis mewakili konvolusi gambar dengan matriks filter. Dalam hal ini, setiap piksel dalam gambar diganti dengan jumlah piksel terdekat yang diambil dengan faktor bobot tertentu.

Filter disebut Gaussian karena dibangun dari fungsi yang dikenal sebagai Gaussian, $$$e ^ {- x ^ 2}$:



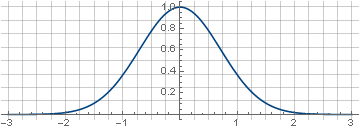
versi dua dimensi yang diperoleh dengan rotasi tentang sumbu ordinat, $$$e ^ {- (x ^ 2 + y ^ 2)}$:



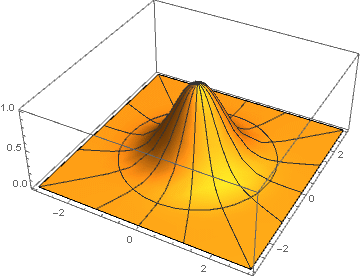
Di sini untuk setiap pasangan koordinat $$$(x, y)$jarak ke pusat dihitung dengan rumus $$$\ sqrt {x ^ 2 + y ^ 2}$, yang diteruskan sebagai argumen ke fungsi Gaussian - dan, seperti yang dapat Anda lihat dengan mudah, $$$e ^ {- \ kiri (\ sqrt {x ^ 2 + y ^ 2} \ kanan) ^ 2}$dikurangi menjadi $$$e ^ {- (x ^ 2 + y ^ 2)}$.

Matriks dibangun pada segmen $$$[- 3.3]$dan dengan beberapa tingkat pengambilan sampel, akan terlihat seperti ini:

$$

$$\ left (\ begin {array} {ccccccc} 1.52 \ kali 10 ^ {- 8} & 2.26 \ kali 10 ^ {- 6} & 0.0000454 & 0.000123 & 0.0000454 & 2.26 \ kali 10 ^ {- 6} & 1.52 \ kali 10 ^ {- 8} \\ 2,26 \ kali 10 ^ {- 6} & 0,000335 & 0,00674 & 0,0183 & 0,00674 & 0,000335 & 2,26 \ kali 10 ^ {- 6} \\ 0,0000454 & 0,0067 & 0,135 & 0,368 & 0,135 & 0,00674 & 0,0000454 \\ 0,000123 & 0,0183 & 0,368 & 1,008 & 0,0183 & 0,000123 \\ 0,0000454 & 0,005 & 0,135 & 0,135 & 0,008 & 0,005 & 0,005454 & 0,005454 \\ 2,26 \ kali 10 ^ {- 6} & 0,000335 & 0,006735 & 0,0183 & 0,00674 & 0,000335 & 2,26 \ kali 10 ^ {- 6} \\ 1,52 \ kali 10 ^ {- 8} & 2,26 \ kali 10 ^ {- 6} & 0,0000454 & 0,000123 & 0,0000454 & 2,26 \ kali 10 ^ { -6} & 1,52 \ kali 10 ^ {- 8} \\ \ end {array} \ kanan)$$

Atau, jika kita menganggap nilai elemen matriks sebagai tingkat kecerahan, seperti ini:



Dalam hal pemrosesan sinyal, ini disebut respon impuls, karena inilah yang merupakan hasil dari konvolusi filter ini dengan impuls tunggal (dalam kasus ini, sebuah piksel) akan terlihat.

Awalnya, Gaussian didefinisikan pada interval yang tak terbatas. Tetapi karena fakta bahwa itu meluruh agak cepat, adalah mungkin untuk mengecualikan dari nilai perhitungan mendekati nol - karena mereka masih tidak akan mempengaruhi hasilnya. Dalam aplikasi nyata, normalisasi nilai juga diperlukan agar setelah konvolusi kecerahan gambar tidak berubah; dan dalam kasus mengaburkan gambar di mana setiap piksel memiliki warna yang sama, gambar itu sendiri tidak boleh berubah.

Untuk kenyamanan, normalisasi juga sering digunakan dalam koordinat, dengan memperkenalkan parameter tambahan $$$\ sigma$(baca "sigma") - untuk mempertimbangkan argumen dalam kisaran $$$[- 1,1]$, dan $$$\ sigma$menentukan rasio kompresi Gaussian:

$$

$$\ frac {e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}}} {2 \ pi \ sigma ^ 2}$$

Pembagi Normalisasi $$$2 \ pi \ sigma ^ 2$diperoleh di sini secara analitik melalui integral tak terhingga pada tak terhingga:

$$

$$\ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}} \, dx dy = 2 \ pi \ sigma ^ 2$$

Karena kenyataan bahwa kesetaraan berlaku $$$e ^ {- \ kiri (x ^ 2 + y ^ 2 \ kanan)} = e ^ {- x ^ 2} e ^ {- y ^ 2}$Gaussian blurring dapat diimplementasikan secara berurutan, pertama di baris dan kemudian di kolom - yang memungkinkan Anda untuk menyimpan cukup banyak perhitungan. Dalam hal ini, perlu menggunakan rumus normalisasi untuk kasus satu dimensi -

$$

$$\ frac {e ^ {- \ frac {x ^ 2} {2 \ sigma ^ 2}}} {\ sqrt {2 \ pi \ sigma ^ 2}}$$

Mulai

Untuk filter sewenang-wenang, pertama-tama kita perlu mendefinisikan fungsi atenuasi kita sendiri dari satu variabel $$$f$, dari mana fungsi dua variabel diperoleh dengan rotasi dengan mengganti $$$x$pada $$$\ sqrt {x ^ 2 + y ^ 2}$dimana $$$x$dan $$$y$ini adalah koordinat elemen matriks dalam rentang $$$(- 1,1)$, dan yang selanjutnya digunakan untuk mengisi elemen matriks. Normalisasi tidak akan dianggap analitis, tetapi penjumlahan langsung dari semua elemen matriks - ini lebih sederhana dan lebih akurat - karena setelah diskritisasi fungsi tersebut "menipis" dan nilai normalisasi akan tergantung pada tingkat diskritisasi.

Dalam kasus elemen-elemen matriks diberi nomor dari awal, koordinat $$$x$atau $$$y$dihitung dengan rumus

$$

$$\ frac {2 index} {size-1} -1$$

dimana $$$index$- nomor seri elemen di baris atau kolom, dan $$$size$- jumlah total elemen.

Misalnya, untuk matriks 5 kali 5, akan terlihat seperti ini:

$$

$$\ kiri (\ mulai {array} {ccccc} f (-1, -1) & f \ kiri (- \ frac {1} {2}, - 1 \ kanan) & f (0, -1) & f \ kiri (\ frac {1} {2}, - 1 \ kanan) & f (1, -1) \\ f \ kiri (-1, - \ frac {1} {2} \ kanan) & f \ kiri (- \ frac {1} {2}, - \ frac {1} {2} \ kanan) & f \ kiri (0, - \ frac {1} {2} \ kanan) & f \ kiri (\ frac { 1} {2}, - \ frac {1} {2} \ kanan) & f \ kiri (1, - \ frac {1} {2} \ kanan) \\ f (-1.0) & f \ kiri (- \ frac {1} {2}, 0 \ kanan) & f (0,0) & f \ kiri (\ frac {1} {2}, 0 \ kanan) & f (1,0) \\ f \ kiri (-1, \ frac {1} {2} \ kanan) & f \ kiri (- \ frac {1} {2}, \ frac {1} {2} \ kanan) & f \ kiri (0, \ frac {1} {2} \ kanan) & f \ kiri (\ frac {1} {2}, \ frac {1} {2} \ kanan) & f \ kiri (1, \ frac {1} {2 } \ kanan) \\ f (-1,1) & f \ kiri (- \ frac {1} {2}, 1 \ kanan) & f (0,1) & f \ kiri (\ frac {1} { 2}, 1 \ kanan) & f (1,1) \\ \ end {array} \ kanan)$$

Atau, jika kita mengecualikan nilai batas yang masih nol, maka koordinat akan dihitung oleh rumus

$$

$$\ frac {2 ukuran indeks + 1} {ukuran}$$

dan matriks akan mengambil formulir

$$

$$\ kiri (\ mulai {array} {ccccc} f \ kiri (- \ frac {4} {5}, - \ frac {4} {5} \ kanan) & f \ kiri (- \ frac {2} { 5}, - \ frac {4} {5} \ kanan) & f \ kiri (0, - \ frac {4} {5} \ kanan) & f \ kiri (\ frac {2} {5}, - \ frac {4} {5} \ kanan) & f \ kiri (\ frac {4} {5}, - \ frac {4} {5} \ kanan) \\ f \ kiri (- \ frac {4} {5 }, - \ frac {2} {5} \ kanan) & f \ kiri (- \ frac {2} {5}, - \ frac {2} {5} \ kanan) & f \ kiri (0, - \ frac {2} {5} \ kanan) & f \ kiri (\ frac {2} {5}, - \ frac {2} {5} \ kanan) & f \ kiri (\ frac {4} {5}, - \ frac {2} {5} \ kanan) \\ f \ kiri (- \ frac {4} {5}, 0 \ kanan) & f \ kiri (- \ frac {2} {5}, 0 \ kanan ) & f (0,0) & f \ kiri (\ frac {2} {5}, 0 \ kanan) & f \ kiri (\ frac {4} {5}, 0 \ kanan) \\ f \ kiri ( - \ frac {4} {5}, \ frac {2} {5} \ kanan) & f \ kiri (- \ frac {2} {5}, \ frac {2} {5} \ kanan) & f \ kiri (0, \ frac {2} {5} \ kanan) & f \ kiri (\ frac {2} {5}, \ frac {2} {5} \ kanan) & f \ kiri (\ frac {4} {5}, \ frac {2} {5} \ kanan) \\ f \ kiri (- \ frac {4} {5}, \ frac {4} {5} \ kanan) & f \ kiri (- \ frac {2} {5}, \ frac {4} {5} \ kanan) & f \ kiri (0, \ frac {4} {5} \ kanan) & f \ kiri (\ frac {2} {5}, \ frac {4} {5} \ kanan) & f \ kiri (\ frac {4} {5}, \ frac {4} {5} \ kanan) \\ \ end {array} \ kanan)$$

Setelah elemen matriks dihitung dengan rumus, perlu untuk menghitung jumlah mereka dan membagi matriks ke dalamnya. Misalnya, jika kita mendapatkan matriks

$$

$$\ kiri (\ mulai {array} {ccc} 1 & 4 & 1 \\ 4 & 20 & 4 \\ 1 & 4 & 1 \\ \ end {array} \ kanan)$$

maka jumlah semua elemennya akan menjadi 40, dan setelah normalisasi akan mengambil bentuk

$$

$$\ left (\ begin {array} {ccc} \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ frac {1} {10} & \ frac {1} {2} & \ frac {1} {10} \\ \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ end {array } \ kanan)$$

dan jumlah semua elemennya menjadi 1.

Redaman linear

Pertama, ambil fungsi yang paling sederhana - baris:

$$

$$\ left \ {\ begin {array} {ll} 1-x, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ kanan.$$

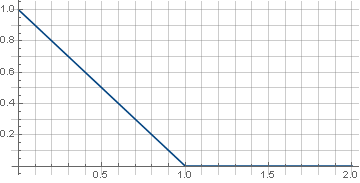
Definisi kontinu piecewise di sini mensyaratkan bahwa fungsi dijamin pergi ke nol dan tidak ada artefak yang muncul di sudut-sudut matriks selama rotasi. Selain itu, karena rotasi menggunakan akar jumlah kuadrat dari koordinat, yang selalu positif, itu cukup untuk menentukan fungsi hanya di bagian positif dari nilai. Sebagai hasilnya, kita mendapatkan:

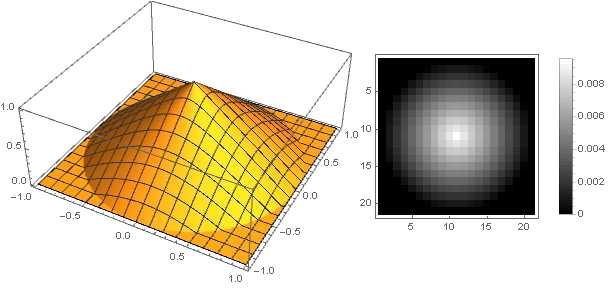
Redaman linear lunak

Transisi yang tajam dari garis miring ke fungsi nol dapat menyebabkan kontradiksi dengan rasa keindahan. Untuk mengatasinya, fungsi tersebut akan membantu kita.

$$

$$1- \ frac {n x-x ^ n} {n-1}$$

di mana $$$n$menentukan "kekakuan" docking, $$$n> 1$. Sebagai contoh $$$n = 3$kita dapatkan

$$

$$\ left \ {\ begin {array} {ll} 1- \ frac {3 xx ^ 3} {2}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ kanan.$$

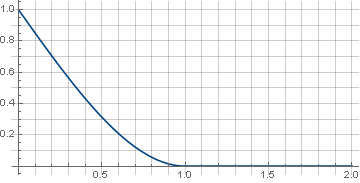
dan filter itu sendiri akan terlihat seperti

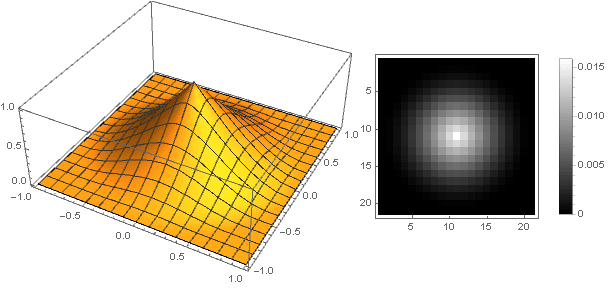
Atenuasi hiperbolik

Filter dapat dibuat lebih "tajam" dan lebih lancar menuju nol dengan mengambil fungsi lain, misalnya, hiperbola, dan memastikan transisi yang mulus ke nol dengan menjumlahkan dengan parabola.



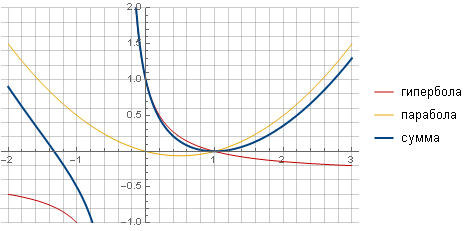
Setelah semua perhitungan dan penyederhanaan, kami mendapatkan formula

$$

$$\ left \ {\ begin {array} {ll} \ frac {(x-1) ^ 2 (k x + k + 1)} {(k + 1) (k x + 1)}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ benar.$$

di mana parameter $$$k> 0$menentukan sifat atenuasi:



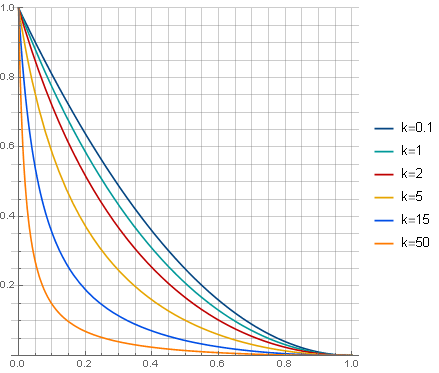
dan filter itu sendiri akan mencari (untuk $$$k = 5$) bagaimana

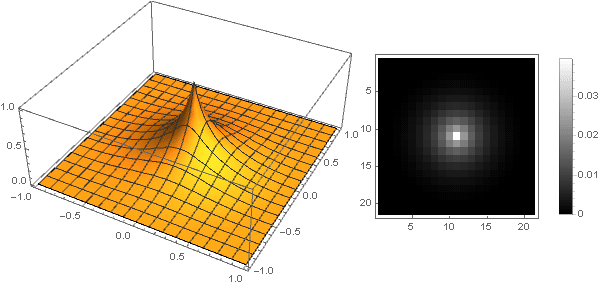
Efek Bokeh

Anda dapat memilih cara lain - untuk membuat bagian atas filter tidak tajam, tetapi bodoh. Cara termudah untuk mengimplementasikan ini adalah dengan menetapkan fungsi redaman sebagai konstanta:

$$

$$\ left \ {\ begin {array} {ll} 1, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ kanan.$$

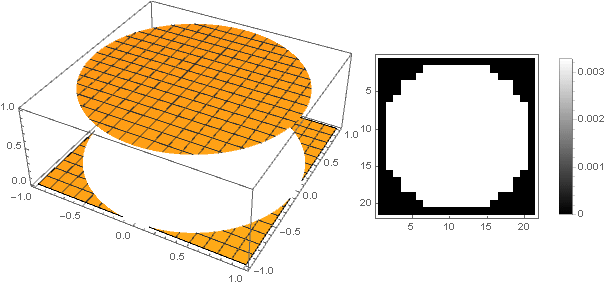
Namun dalam hal ini, kita mendapatkan pixelation yang kuat, yang kontras dengan indera keindahan. Untuk membuatnya lebih halus di tepi, parabola tingkat tinggi akan membantu kita, dari mana, dengan menggerakkannya sepanjang sumbu ordinat dan mengkuadratkannya, kita mendapatkan

$$

$$\ left \ {\ begin {array} {ll} \ kiri (1-x ^ n \ kanan) ^ 2, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ kanan.$$

Memvariasikan parameter $$$n$Anda bisa mendapatkan berbagai opsi filter:

$$

$$n = 0,5$$

$$

$$n = 2$$

$$

$$n = 10$$

$$

$$n = 50$$

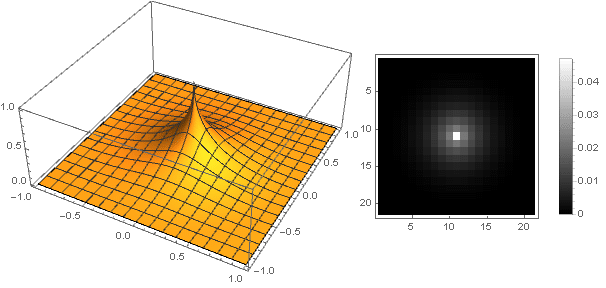
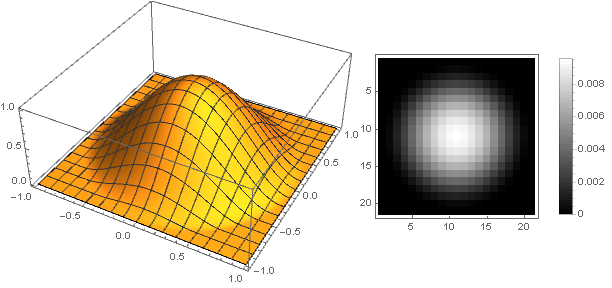
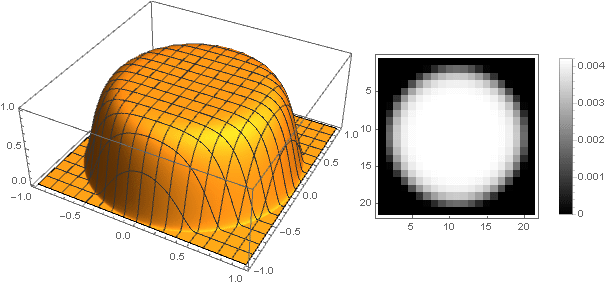
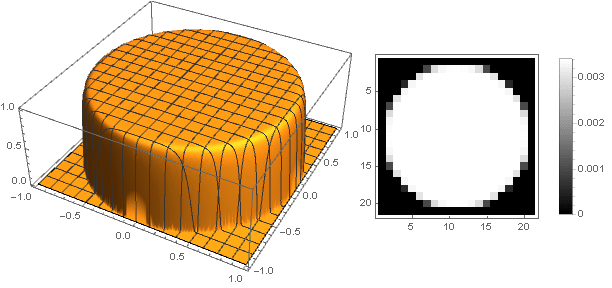
Dan dengan sedikit memodifikasi fungsi redaman, Anda dapat membuat cincin di tepi filter lebih jelas, misalnya seperti ini:

$$

$$\ kiri \ {\ begin {array} {ll} \ kiri (1-x ^ n \ kanan) ^ 2 \ kiri (d + x ^ m \ kanan), & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ benar.$$

Parameter di sini $$$d$menentukan ketinggian pusat, dan $$$m$- Ketajaman transisi ke tepi.
Untuk $$$d = 0,2, m = 2, n = 10$kita dapatkan



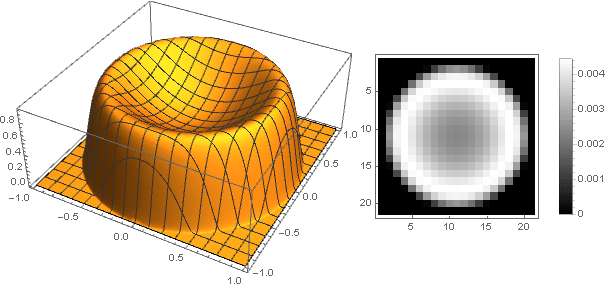
tapi untuk $$$d = 0, m = 12, n = 2$

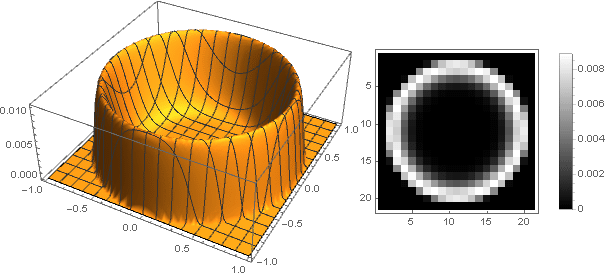
Variasi Gaussian

Fungsi Gaussian itu sendiri juga dapat dimodifikasi secara langsung. Cara yang paling jelas untuk melakukan ini adalah membuat parameter eksponen - kita tidak akan mempertimbangkannya sekarang, tetapi mengambil opsi yang lebih menarik:

$$

$$\ left \ {\ begin {array} {ll} e ^ {\ frac {kx ^ 2} {x ^ 2-1}}, & -1 <x <1 \\ 0, & jika tidak \\ \ end { array} \ benar.$$

Karena kenyataan itu dengan $$$x$unit-penyebut $$$x ^ 2-1$cenderung nol fraksi $$$\ frac {k x ^ 2} {x ^ 2-1}$cenderung minus tak terhingga, dan eksponen itu sendiri juga cenderung nol. Jadi membaginya dengan $$$x ^ 2-1$memungkinkan untuk mengompres domain definisi fungsi dengan $$$(- \ infty, \ infty)$sebelumnya $$$(- 1,1)$. Apalagi kapan $$$x = \ pm 1$karena pembagian dengan nol ( $$$1 ^ 2-1 = 0$) nilai fungsi tidak didefinisikan, tetapi memiliki dua batas - batas di satu sisi (dari dalam) adalah nol, dan di sisi lain, tak terhingga:

$$

$$\ underset {x \ to 1 ^ -} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = 0$$

$$

$$\ underset {x \ to 1 ^ +} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = \ infty$$

Karena nilai batas tidak termasuk dalam interval, maka nol dalam batas di satu sisi saja sudah cukup. Menariknya, properti ini meluas ke semua turunan dari fungsi ini, yang memastikan pencocokan sempurna dengan nol.

Parameter $$$k$menentukan kemiripan dengan Gaussian - semakin besar, semakin kuat kemiripan yang diperoleh - karena fakta bahwa bagian yang semakin linier $$$\ frac {1} {x ^ 2-1}$jatuh di tengah fungsi. Orang bisa berasumsi bahwa karena ini, dalam batasnya, Anda bisa mendapatkan Gaussian asli - tetapi, sayangnya, tidak - fungsinya masih berbeda.



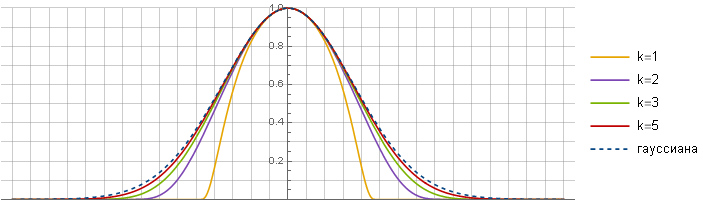
Sekarang Anda dapat melihat apa yang terjadi:

$$

$$k = 5$$

$$

$$k = 2$$

$$

$$k = 0,5$$

$$

$$k = 0,1$$

$$

$$k = 0,01$$

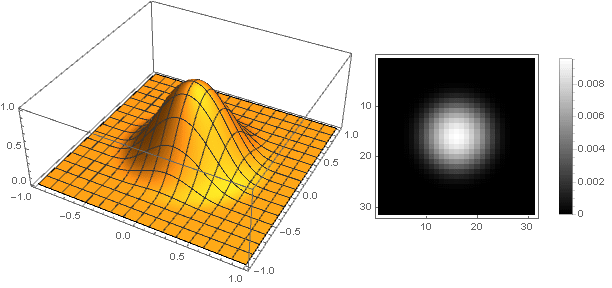
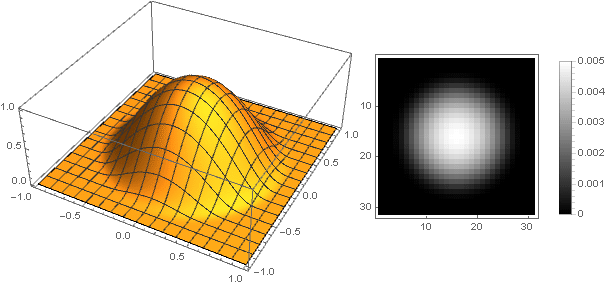
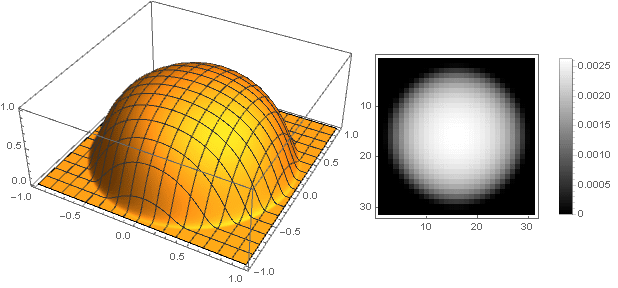
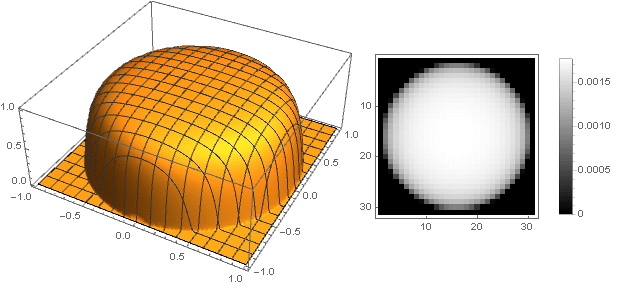
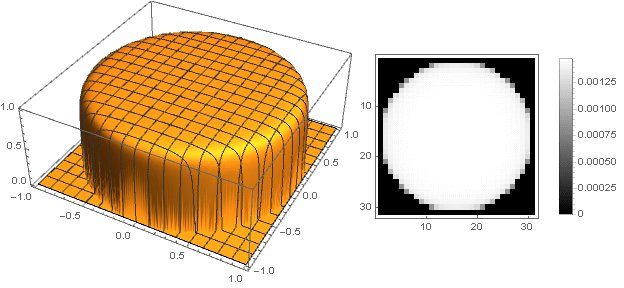
Variasi bentuk

Dengan mengubah fungsi transisi dari dua koordinat ke satu $$$\ sqrt {x ^ 2 + y ^ 2}$, Anda bisa mendapatkan bentuk lain, bukan hanya disk. Sebagai contoh:

$$

$$f \ kiri (\ frac {\ kiri | x-y \ kanan | + \ kiri | x + y \ kanan |} {2} \ kanan)$$

$$

$$f (\ kiri | x \ kanan | + \ kiri | y \ kanan |)$$

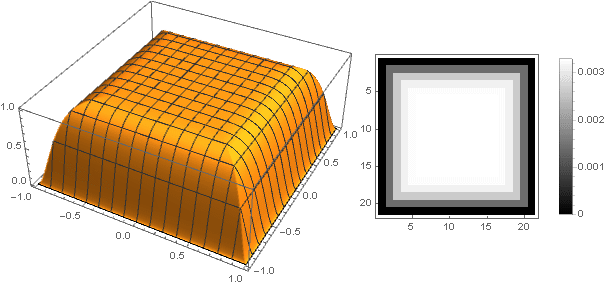
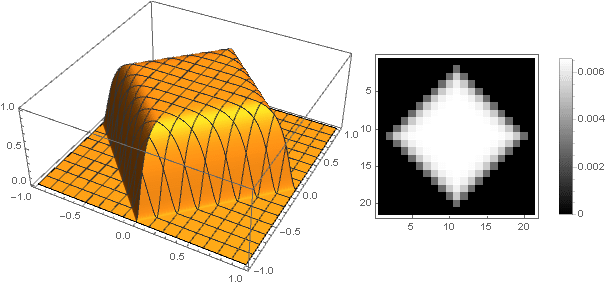
Dengan berpindah ke bilangan kompleks, Anda dapat membuat angka yang lebih kompleks:

$$

$$f \ kiri (\ frac {\ kiri | \ Re \ kiri ((x + iy) (-1) ^ {\ frac {0} {3}} \ kanan) \ kanan | + \ kiri | \ Re \ kiri ((x + iy) (-1) ^ {\ frac {1} {3}} \ kanan) \ kanan | + \ kiri | \ Re \ kiri ((x + iy) (-1) ^ {\ frac { 2} {3}} \ kanan) \ kanan |} {\ sqrt {3}} \ kanan)$$

$$

$$f \ biggl (10 \ kiri | \ Re \ kiri ((x + iy) (-1) ^ {\ frac {1} {8}} \ kanan) \ kanan | \ biggr) \ cdot f (\ kiri | x + iy \ benar |)$$

$$

$$f \ biggl (\ biggl | 5 \ kiri | x + iy \ kanan | (x + iy) \ Re \ biggl (\ cos \ kiri (\ frac {5} {2} \ arg (x + iy) \ kanan ) \ biggr) \ biggr | \ biggr) \ cdot f (\ kiri | x + iy \ kanan |)$$

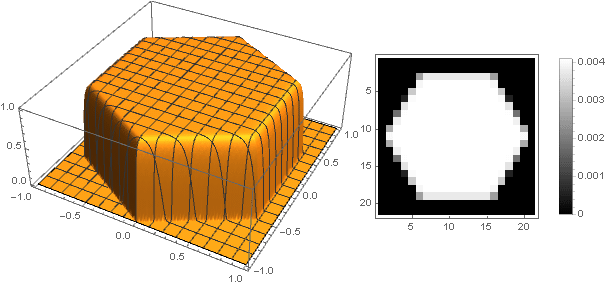
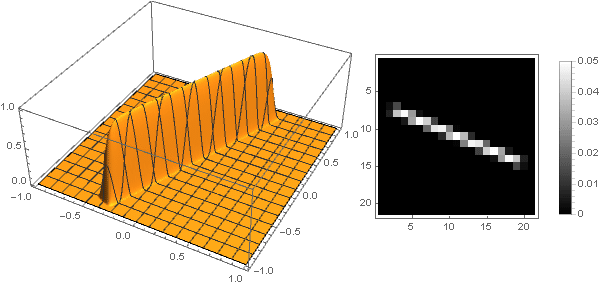
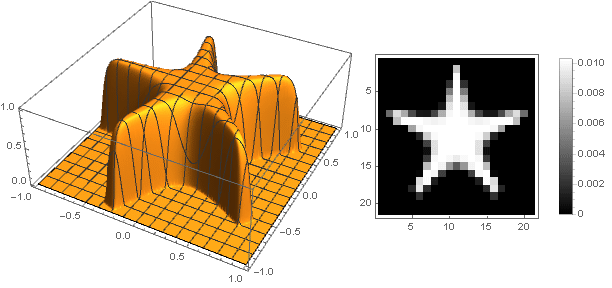
Dalam hal ini, Anda harus memastikan bahwa saat mengonversi koordinat tidak melampaui interval $$$(0,1)$- baik, atau sebaliknya, mendefinisikan kembali fungsi redaman untuk nilai negatif dari argumen.

Beberapa contoh spesifik

Artikel tidak akan lengkap tanpa pengujian praktis pada gambar tertentu. Karena kami tidak memiliki karya ilmiah, kami juga tidak akan mengambil gambar Lena - kami akan mengambil sesuatu yang lembut dan halus:


















Filter yang sama, tetapi untuk teks:

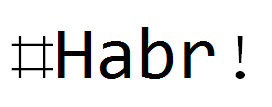
Kesimpulan

Demikian pula, Anda dapat membuat filter yang lebih kompleks, termasuk yang memiliki penajaman atau garis besar; dan juga memodifikasi yang sudah dipertimbangkan.

Yang menarik adalah penyaringan nonlinier, ketika nilai koefisien filter tergantung pada koordinat atau gambar yang disaring secara langsung - tetapi ini sudah menjadi subjek untuk penelitian lain.

Secara lebih rinci, derivasi fungsi untuk docking dengan konstanta dipertimbangkan di sini . Fungsi-fungsi jendela yang dipertimbangkan di sini juga dapat digunakan sebagai fungsi atenuasi - yang diperlukan hanyalah skala argumen c (0,1) ke ( $$$\ frac {1} {2}$, 1) atau awalnya mempertimbangkan fungsi jendela dengan rumus $$$\ frac {1} {2} \ kiri (f \ kiri (\ frac {t x + 1} {t-1} \ kanan) -f \ kiri (\ frac {t x-1} {t-1} \ benar) \ benar)$.

Dokumen sumber Wolfram Mathematica untuk artikel ini dapat diunduh di sini .