Alih-alih kata pengantar
Misalkan, duduk di kursi hangat di malam hari, sebuah pikiran gila terjadi pada Anda: "Hmm, mengapa saya tidak mencari tahu mengapa model hiperparameter dipilih secara acak dan mengapa semuanya bekerja?"
Ini adalah lereng yang licin - Anda pikir beberapa malam dengan membaca santai bab "Belajar Dalam" atau klip youtube 5 menit dari berbagai MOOC sudah cukup; pada kenyataannya, untuk menciptakan pemahaman, dan bukan ilusi, diperlukan waktu yang layak (well, tentu saja tidak kurang dari enam bulan untuk yang paling fanatik); tetapi hal yang paling menyedihkan adalah bahwa keuntungan dari acara ini tidak jelas - untungnya (atau sayangnya), dunia tidak diatur menurut hukum matematika, dan jika Anda seorang dokter fisika dan fisika tiga kali, beberapa model akan bekerja lebih baik hanya jika Anda memasukkan mereka memiliki lebih banyak data pra-pemrosesan atau membangun ansambel besar.
Saya menganggap itu tugas saya untuk memperingatkan Anda bahwa ini adalah jalur kurva, dan ada kemungkinan bahwa investasi dalam matematika tidak akan membuahkan hasil secepat yang kita inginkan. Tapi matematika itu sendiri menarik, aplikasinya pun apa. Terlebih lagi, jika Anda tertarik, dan apa yang terjadi di kotak hitam ini dengan hyperparameter, maka ini berarti bahwa matematika kemungkinan besar tidak acuh terhadap Anda.
Sesuatu yang lain tentang rekomendasi saya: Saya tidak suka literatur matematika, yang penuh dengan indeks, mutiara seperti "a_ijk dengan tiga garis bawah dan topi konjugat". Saya percaya bahwa ide lebih penting daripada kesimpulan yang teliti. Pada saat yang sama, ide tidak boleh jatuh ke "tangan", semuanya harus cukup ketat. Saya tidak suka buku-buku seperti Bourbaki dan Knut. Menurut pendapat saya, buku-buku ini dimaksudkan untuk apa saja, tetapi tidak untuk membaca dan bukan untuk mempelajari subjek. Mereka bagus sebagai tautan dan sebagai ensiklopedi.
Pada akhirnya, saya akan mengutip sesuatu dari Bertrand Russell:
Euclid membenci utilitas praktis yang diperkenalkan Plato. Mereka mengatakan bahwa satu siswa, setelah mendengarkan bukti, bertanya apa yang dia menangkan dengan mempelajari geometri; kemudian Euclid memanggil seorang budak dan berkata: "Berikan satu sen muda pada pemuda itu, karena dia pasti mendapat manfaat dari apa yang dia pelajari."
Sekarang saya akan pindah ke bagian utama.
Prasyarat
- Saya berasumsi bahwa Anda sedikit banyak berorientasi pada pelajaran matematika di sekolah.
- Saya berasumsi bahwa Anda tidak sepenuhnya dalam bahasa Inggris dengan "Anda," karena banyak literatur dan kursus yang baik ditulis dan diceritakan dalam bahasa itu. Bahasa Inggris matematika tidak seseram bahasa Inggris pada umumnya; ini adalah kosakata yang agak terbatas dengan kalimat yang dibangun secara standar, tanpa kesalahan waktu, tanpa kerusuhan warna, dll.
- Saya berasumsi bahwa Anda memiliki tali yang dapat Anda ikat sendiri ke kursi.
Tingkat kesulitan
Bukan rahasia bahwa banyak literatur telah ditulis pada setiap disiplin matematika, dan kadang-kadang bahkan pilihan sederhana dari buku yang tepat menjadi masalah. Saya akan menyoroti beberapa tingkat kompleksitas dalam literatur yang Anda tahu harus ikut campur dan ke mana harus mendaki (sejauh ini) tidak perlu (atau apa yang dapat Anda lihat untuk mendapatkan informasi yang lebih lengkap).
- Bawa - pekerja keras utama; Ini adalah buku-buku yang disebut "must have".
- Terluka saya banyak - level lebih tinggi, memungkinkan Anda untuk melihat level 1 dari pandangan burung, mensistematisasikan pengetahuan, menggabungkan berbagai bidang pengetahuan.
- Mimpi buruk - untuk semangat yang kuat, tingkat mehmat, untuk pecinta matematika dan menara gading.
Peta jalan
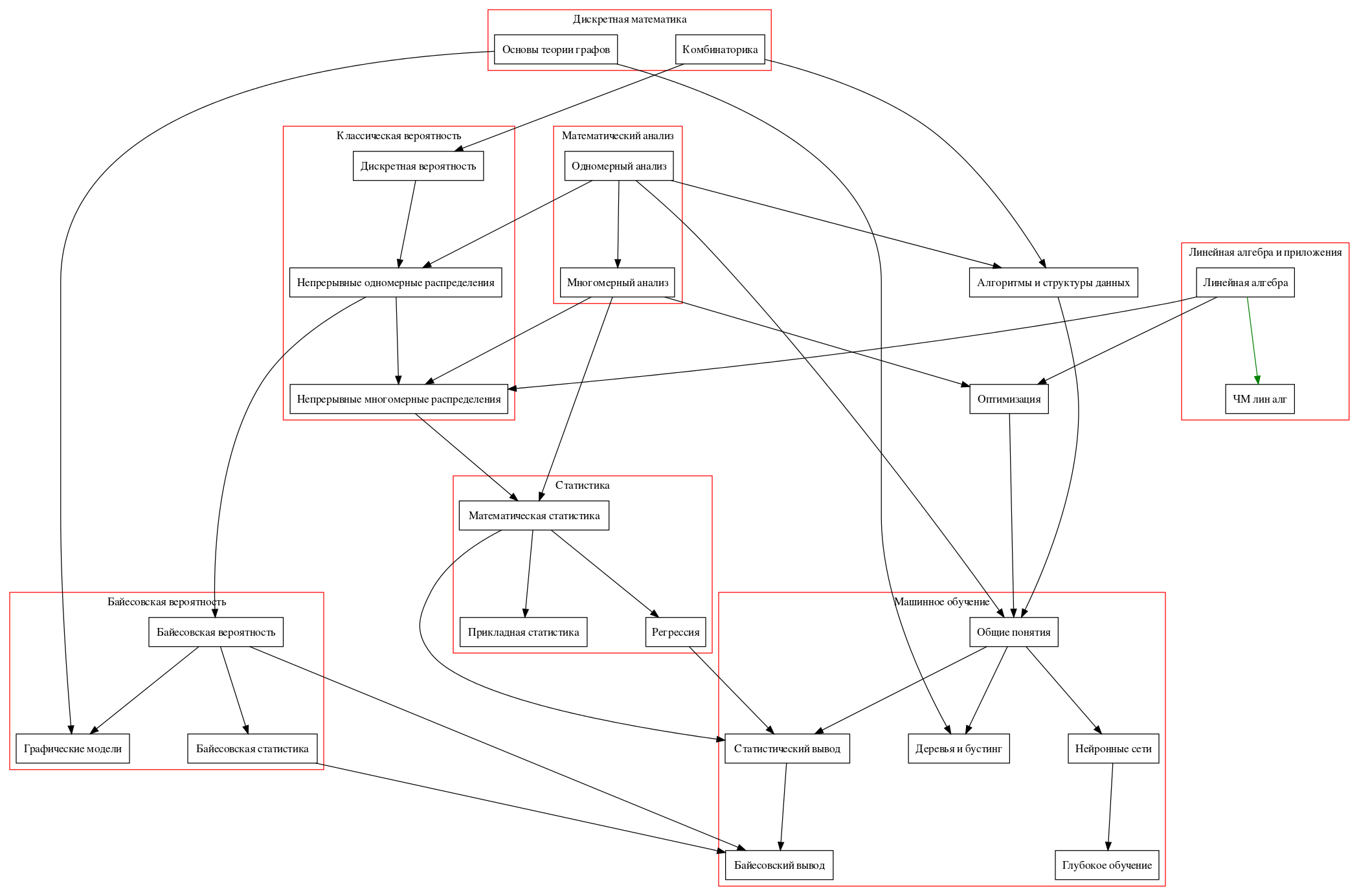
Sebenarnya saya akan lulus untuk kursus tertentu.
Analisis, dia adalah kalkulus
Dia diajarkan dengan cukup menarik di universitas-universitas Rusia: kebanyakan dari mereka, beberapa tahun setelah akhir kursus, samar-samar hanya ingat beberapa integral di sana, dan sesuatu yang lain tampaknya. Dan ini terlepas dari kenyataan bahwa analisis adalah disiplin, pada kenyataannya, salah satu yang mendasar dalam matematika secara umum. Sebagai aturan, tidak ada jembatan dari teori ke praktek, dan kursus ini, seperti pulau terbang, melayang di suatu tempat di kepala, benar-benar bercerai dari kehidupan nyata. Penting untuk mengatasi ini dengan menyelesaikan masalah, apalagi, tidak hanya dari bidang matematika, tetapi juga sesuatu dari "kehidupan nyata" diinginkan.
Apa yang perlu Anda ketahui dari analisis?
Hal-hal utama yang akan kita butuhkan adalah konsep batas, kontinuitas, turunan, fungsi banyak variabel, gradien, integral, integral dengan batas atas variabel, integral multidimensi *.
Sastra
Bawa : semuanya lebih atau kurang standar di sini -
Piskunov / Fichtenholtz .
Banyak yang menyakitiku :
Zorich, Volume 1 . Saya sangat menyukai buku ini; ini bukan buku teks, tetapi novel dalam formula, sesuatu seperti Eugene Onegin. Sayangnya, ini lebih rumit daripada kursus analisis standar karena kenyataan bahwa banyak hal di dalamnya diberikan secara lebih umum, dan Anda perlu membiasakan diri dengannya; tetapi karena kesamaan ini banyak hal yang berbeda dihubungkan bersama (lihat batas yang sama di pangkalan).
Nightmare :
Zorich Volume 1 + Volume 2, Rudin "Dasar-dasar Analisis Matematika", Lviv "Kuliah tentang Analisis Matematika", Ramanan "Global Calculus".Secara umum, ringkasan di sini adalah ini: literatur analisis, bahkan dalam bahasa Rusia, penuh; buku teks cenderung murni matematika. Sebagai tambahan untuk buku teks level 2-3, saya dapat menyarankan beberapa kursus:
Saya tidak melihat kursus dari ruang kuliah MIPT tentang analisis, tetapi untuk kelengkapan saya juga akan memberikan:
Berlatih
Berlatih dan menerapkan pengetahuan yang diperoleh tidak hanya "opsional", tetapi sangat wajib, jika tidak seluruh teori akan bergantung pada Anda dengan bobot mati, dan Anda akan dengan cepat tenggelam ke dasar tanpa menyadarinya.
Saya mengusulkan untuk mempertimbangkan pilihan berikut:
Demidovich, set masalah dari program MIT (https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/index.htm)
Aljabar linier
Roti harian untuk Ilmu Data dan untuk ilmu pengetahuan secara umum. Sayangnya, orang telah belajar untuk menyelesaikan dengan baik hanya persamaan linear dan sistem mereka; untuk persamaan derajat 2 dan di atas, ada segala macam teori yang sangat tidak sepele (aljabar komutatif, geometri aljabar, dan lain-lain seperti mereka). Oleh karena itu, dalam analisis data, model linier terutama digunakan (atau model linier umum, seperti regresi logistik, perceptron, dll.).
Ada banyak buku tentang aljabar linier dalam bahasa Rusia. Masalahnya adalah bahwa mereka ditulis baik untuk ahli matematika, atau ada banyak indeks di dalamnya (dan tidak ada hutan terlihat di belakang pohon). Seringkali penekanan dalam kursus universitas adalah pada formulir Jordan; bentuk standar lainnya sering tidak disebutkan; ada Gauss dan Kramer bodoh, tetapi jarang apa yang terjadi tentang LU, tentang SVD.
Apa yang perlu Anda ketahui dari aljabar linier?
Konsep vektor dan ruang vektor; konsep operator linier; komunikasi operator dan matriks; dekomposisi matriks (setidaknya LU, SVD); vektor eigen dan nilai eigen; orthogonal, operator kesatuan; operator simetris dan hermitian; bentuk kuadratik, reduksi ke sumbu utama.
Sastra
Bawa :
Kursus Gilbert Strang OCW-MIT tentang aljabar linear + bukunya .
ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/index.htmHal terbaik tentang kursus ini adalah kurangnya teorema aljabar linier yang "kompleks" dan agak bodoh, semua jenis ruang ganda, sejumlah besar masalah dalam buku ini, pendekatan berorientasi praktik (bukan "apa itu," tetapi "bagaimana cara menghitungnya"). Lebih banyak program penjelasan dalam aljabar linier yang belum saya temui.
Banyak yang terluka :
Axler “Aljabar linier dikerjakan dengan benar”; Gelfand "Kuliah tentang aljabar linier "; Kursus MIPT
lectoriy.mipt.ru/course/LinearAlgebra ;
Kostrikin "Pengantar Aljabar, Bagian 2", Tyrtyshnikov "Analisis Matriks dan Aljabar Linier".Masalah dengan buku dan kursus dari tingkat kerumitan ini adalah bahwa mereka secara teori berorientasi. Ada fungsional linier dan ruang ganda, tetapi tidak ada matriks proyeksi pada ruang bagian dan metode praktis untuk menghitung nilai eigen. Kemungkinan besar, kursus dari tingkat ini harus dilengkapi dengan praktik yang kuat; misalnya dengan metode numerik aljabar linier.
Tentang buku terakhir secara terpisah. Menurut pendapat saya, ini adalah salah satu buku berbahasa Rusia yang paling sukses tentang aljabar linier dalam arti bahwa buku ini tidak terlalu bercerai dari praktik; pada saat yang sama, ini berisi segala macam topik "lanjutan". Hingga taraf tertentu, ini dapat sepenuhnya menggantikan kuliah Strang, tetapi perlu ditambah dengan tugas-tugas sederhana untuk "mengisi tangan Anda". Ada masalah dalam buku ini, tetapi mereka cukup parah.
Mimpi buruk :
Kostrikin-Manin "Aljabar Linier dan Geometri", Shafarevich-Remizov "Aljabar Linier dan Geometri".Secara umum, ada banyak literatur yang bagus di Rusia, terutama di tingkat terakhir, tetapi menderita kompleksitas yang berlebihan.
Berlatih
Seperti dalam kasus pertama, latihan diperlukan. Go SVD - Pelajari Kompresi Gambar. Pergi melalui perkalian matriks - pelajari transformasi Fourier cepat, algoritma Strassen; menyelesaikan banyak masalah (misalnya, dari
buku masalah Kostrikin atau Proskuryakov ); tulis dekomposisi LU Anda, Gauss. Untuk yang paling gigih, saya dapat menawarkan buku-buku bagus tentang metode numerik aljabar linier, seperti
Trefethen, Bau "NUMERICAL LINEAR ALGEBRA"; Horn, Johnson "Analisis Matriks" . Buku-buku ini akan berguna, pertama-tama, untuk "mengisi" tangan Anda; kedua, akan segera menjadi jelas bahwa banyak metode teoritis dipecah menjadi chip tentang prosa kehidupan (akurasi mesin, ketidakstabilan metode, bekerja dengan matriks jarang).
Matematika diskrit
Paus CS modern lainnya. Di sini kita terutama tertarik pada kombinatorik dan dasar-dasar teori grafik.
Apa yang perlu Anda ketahui dari teori kombinatorik dan grafik?
Koefisien binomial, asimtotiknya; grafik; pohon; pencarian mendalam dan luas; hubungan rekurensi dan solusi mereka;
Sastra
Bawa :
Anderson J. "Matematika Terpisah dan Combinatorics"; Haggarti, Schlipf J., Whitesides S. "Matematika diskrit untuk programmer", Ore O. "Grafik dan aplikasi mereka .
"Dua buku pertama - Talmud yang sangat baik dalam matematika diskrit, mencakup hampir semua pertanyaan yang perlu Anda ketahui.
Banyak yang terluka saya :
Graham, Knut, Patashnik "Matematika Beton", Harari "Teori Grafik", Bijih "Teori Grafik".Nightmare :
Sachkov "Pengantar Metode Kombinatorial Matematika Diskrit", Omelchenko "Teori Grafik".Berlatih
Sebagai aturan, sejumlah besar masalah dimasukkan dalam buku teks tentang kombinatorik; mereka harus diselesaikan. Faktanya, semua kombinatorik adalah seni memecahkan berbagai masalah, dan bukan teori tunggal.