Teori kebahagiaan. Sandwich sandwich dengan mentega

Saya terus berkenalan dengan para pembaca Habr dengan bab-bab dari bukunya "Theory of Happiness" dengan subtitle "Yayasan Matematika dari Hukum Makna." Ini belum diterbitkan buku sains populer, sangat informal menceritakan tentang bagaimana matematika memungkinkan Anda untuk melihat dunia dan kehidupan orang-orang dengan tingkat kesadaran yang baru. Ini untuk mereka yang tertarik pada sains dan bagi mereka yang tertarik pada kehidupan. Dan karena kehidupan kita kompleks dan, pada umumnya, tidak dapat diprediksi, penekanan dalam buku ini terutama pada teori probabilitas dan statistik matematika. Di sini teorema tidak terbukti dan dasar-dasar sains tidak diberikan, ini sama sekali bukan buku teks, tetapi apa yang disebut ilmu rekreasi. Tetapi justru pendekatan yang hampir menyenangkan yang memungkinkan kami untuk mengembangkan intuisi, mencerahkan kuliah untuk siswa dengan contoh-contoh nyata dan, akhirnya, menjelaskan kepada non-matematikawan dan anak-anak kami bahwa kami menemukan hal-hal menarik dalam ilmu kering kami.



Dalam bab ini, kami memeriksa hukum sandwich dan mengatur seluruh penelitian menggunakan metode Monte Carlo dan analisis dimensi. Dan akhirnya, sanggah mitos populer bahwa minyak adalah penyebab hukum kekejaman ini.

Tema sandwich terjatuh menghantui baik masyarakat umum maupun peneliti. Selama beberapa dekade, percobaan telah dilakukan, film telah diambil, artikel ditulis, roti lapis yang jatuh ditumbuhi legenda dan kesimpulan yang salah. Beberapa tugas yang tidak berharga menarik begitu banyak perhatian, dan jika Anda berpikir bahwa semua ini memanjakan, maka perlu diingat bahwa bahkan penghargaan, bagaimanapun, juga tidak serius, untuk solusinya. Pada 1995, Robert Matthews menerima Hadiah Shnobel untuk karyanya, “Falling Sandwich, Murphy Law, dan Fundamental Constants,” diterbitkan dalam European Journal of Physics. Terlepas dari topik komik dan reaksi yang sesuai dari komunitas ilmiah, ini adalah artikel yang sangat menarik di mana analisis menyeluruh dari proses geser dilakukan dan kesimpulan yang luas dibuat: tidak peduli makhluk antropomorfik apa yang hidup di atmosfer muncul, mereka akan ditakdirkan untuk hukum sandwich. Setelah kemenangan penelitian yang sia-sia, orang dapat menutup topik, tetapi mengapa kehilangan kesempatan untuk mempertimbangkan metode yang menarik dan berguna secara objektif sebagai contoh masalah yang menarik!

Ida melempar sandwich di Monte Carlo!

Kita jarang melempar sandwich seperti koin, setidaknya ketika kita bertambah tua dari dua tahun. Lebih sering daripada tidak, kita tanpa sadar mengulangi tentang percobaan yang sama: sandwich, awalnya ditempatkan dengan mentega ke atas, terlepas dari tangan kita, atau meluncur dari meja. Dalam proses tergelincir, ia berputar, terbang di udara, dan, akhirnya, menjatuhkan diri ke atas meja atau di lantai. Tahap awal musim gugur dipengaruhi oleh sejumlah parameter: gesekan terhadap jari-jari atau permukaan meja, posisi awal sandwich dan kecepatan awalnya, ketinggian musim gugur, dan akhirnya, ukuran sandwich. Kami memiliki sistem dinamis dengan beberapa parameter input dan satu output - posisi sandwich di lantai. Di dalam sistem, seperti dalam kasus koin, hukum mekanis bekerja, yang dijelaskan oleh persamaan diferensial dan bersifat deterministik . Ini berarti bahwa tidak ada kecelakaan di dalamnya - hasilnya hanya bergantung pada data input, dan dengan pengulangan yang tepat dari parameter, kita harus mendapatkan hasil yang identik. Ini berlaku untuk model sandwich, disajikan dalam bentuk sistem persamaan diferensial, tetapi bagaimana dengan sandwich nyata, kasar dan unik, dijatuhkan oleh orang sungguhan di restoran, di jalan, atau di sofa? Keragaman dunia nyata dapat dijelaskan dengan menerapkan parameter acak pada input sistem deterministik.

Namun, bahkan aljabar variabel acak, yang hanya mencakup penjumlahan dan perkalian, bukanlah tugas yang mudah, tetapi kami memiliki persamaan diferensial! Kami tidak memanjat ke alam liar yang menarik ini, tetapi menggunakan teknik yang dikembangkan dengan baik di banyak daerah - metode Monte Carlo . Ini terdiri dalam mengumpulkan statistik dan dalam menentukan sifat-sifat sistem kompleks tertentu sebagai hasil dari pengujian berulang dengan berbagai parameter acak. Saya tekankan lagi: sistem yang diteliti tidak bersifat stokastik dan tidak kacau, dan bereaksi sesuai prediksi terhadap data input acak. Dalam metode Monte Carlo, keacakan diperlukan hanya untuk efisien memilah banyak pilihan sebanyak mungkin dan melihat ke semua "sudut" realistis, mendapatkan ide tentang perilaku sistem.

Bahkan, kami telah menggunakan metode ini, menonton pengendara sepeda di atas bukit dan masih akan menggunakannya dengan mengatur tenggat waktu di kantor dan berbagi uang dalam masyarakat tertutup. Korespondensi satu-ke-satu antara probabilitas dan ukuran volume atau area, yang telah kita bicarakan sebelumnya, memungkinkan kita untuk menggunakan metode Monte Carlo untuk integrasi numerik. Fitur dari percobaan sandwich yang akan datang adalah bahwa kita akan tertarik bukan pada distribusi probabilitas (tepat atau empiris), tetapi pada ketergantungan probabilitas pada parameter masalah. Kami akan mencari jawaban untuk pertanyaan: dalam keadaan apa hukum sandwich dipenuhi? Kami akan menyediakan berbagai parameter khusus untuk input sistem dinamis kami dan mengumpulkan statistik tentang turunnya minyak dan turunnya minyak. Dengan demikian, hasil dari serangkaian percobaan akan menjadi angka - probabilitas minyak jatuh.

Saya yakin bahwa sengaja menjatuhkan sandwich nyata di lantai itu salah, jadi kami akan menggunakan pemodelan matematika. Untuk mengatasi masalah jatuhnya sandwich, saya memilih salah satu simulator dunia fisik yang tersedia yang digunakan untuk membuat game online. Dia diizinkan membuat meja dan lantai virtual, serta dua sandwich. Satu muncul di tepi meja, dan yang kedua - "terlepas dari jarinya", yaitu, tergelincir dari titik dukungan. Adalah kekuatan saya untuk mengatur posisi awal dan sudut sandwich, kecepatan horizontal (kasus menghancurkan sandwich dari meja), koefisien gesek, ukuran sandwich dan ketinggian musim gugur. Eksperimennya terlihat seperti ini:

Eksperimen dengan jatuhnya sandwich virtual di simulator dunia fisik.

Pada saat sandwich menyentuh lantai, sudut sandwich tetap, atau lebih tepatnya, sudut vektor normal. Tanda sinus dari sudut ini akan memberi tahu kita dari sisi mana minyak berubah: case yang berhasil sesuai dengan nilai positif, dan posisi ke bawah sesuai dengan nilai negatif. Hasilnya dimasukkan ke dalam tabel, dan sandwich virtual baru siap untuk jatuh. Tugas yang kami tetapkan adalah ini: untuk menilai kemungkinan sandwich jatuh minyak turun ketika jatuh dari ketinggian tertentu.

Metode Monte Carlo mengasumsikan bahwa variabel acak digunakan sebagai parameter. Dan di sini perlu dikatakan beberapa kata tentang apa variabel acak itu . Mari kita kembali ke ahli matematika dan struktur matematika. Struktur apa yang dapat digunakan untuk mensimulasikan hasil penurunan angka pada dadu, atau ketinggian air di sungai, karena ada kegembiraan yang konstan di atas air? Bagaimana cara bekerja dengan jumlah mobil yang melewati persimpangan dalam satu jam? Struktur apa yang bisa menggambarkan keadaan elektron? Di satu sisi, ini adalah angka-angka spesifik dari set nilai yang terdefinisi dengan baik: untuk sebuah tulang, misalnya, dari suatu set $$$\ {1,2,3,4,5,6 \}$ , dan nilai ini mudah diperoleh dengan melakukan percobaan. Namun, percobaan kedua akan memberikan hasil yang berbeda, ini jelas bukan hanya angka: hari ini adalah satu, besok itu adalah yang lain. Sebuah pertanyaan filosofis bahkan mungkin muncul: apakah masuk akal untuk berbicara tentang beberapa nilai "ketinggian air di sungai", atau jumlah mobil, karena nilai-nilai ini tidak dapat "ditangkap" dan dicatat? Mungkinkah ada, dalam arti tertentu, pengetahuan yang tepat dari variabel acak?

Seringkali, ketika berbicara tentang variabel acak seperti itu, mereka hanya terbatas pada nilai rata-rata, tetapi ini adalah cara yang bagus untuk bingung atau bahkan sengaja dibuat bingung. Dua angka: mean dan standar deviasi, sudah lebih baik, tetapi ini jelas tidak semua informasi tentang objek yang menarik bagi kita. Mungkin ini bukan angka, tapi set? Katakanlah, Anda dapat mencoba menggambarkan ketinggian air di sungai sebagai interval nilai yang mungkin, dengan mempertimbangkan kegembiraan, dan untuk contoh dengan mobil, katakan bahwa dari 1 hingga 100 mobil lewat dalam satu jam, dll. Tetapi mudah untuk melihat bahwa himpunan nilai yang mungkin juga tidak cukup, misalnya, dengan pengulangan pengukuran jumlah mobil di jalan, beberapa angka akan terjadi lebih sering, dan beberapa kita tidak akan menunggu sama sekali. Dalam bab terakhir, kami memperkenalkan ukuran probabilitas sebagai fungsi pada ruang probabilitas. Untuk kuantitas acak, peristiwa dasar ruang ini akan menjadi elemen dari domain definisinya, dan ukuran menentukan distribusi probabilitas untuk kuantitas ini. Dan sekarang ini adalah informasi yang lengkap dan akurat. Suatu fungsi dapat direpresentasikan secara analitik atau sebagai perkiraan oleh fungsi lain, dalam bentuk tabel, histogram, atau dalam bentuk grafik. Semua representasi ini adalah model dari objek yang sama - variabel acak, dan yang paling penting di sini bukanlah tipe representasi yang spesifik seperti sifat matematika dari fungsi ini. Untuk distribusi probabilitas, sifat-sifatnya berbeda: jumlah parameter, jumlah mode, entropi, pembagian tak terhingga, aditivitas, stabilitas, keterpaduan, dan sebagainya. Memodelkan variabel acak yang tidak diketahui yang diperoleh dari percobaan, statistik dari gudang besar dari distribusi yang diketahui dengan sifat yang didefinisikan secara tepat, memilih tidak begitu banyak fungsi "paling mirip", melainkan sebuah fungsi yang paling sepenuhnya bertepatan dalam sifat-sifatnya dengan variabel acak yang diamati. Ini adalah inti dari analisis statistik dan teknik untuk menguji hipotesis statistik yang akrab bagi setiap siswa yang telah menyentuh statistik.

Kami sekarang memiliki masalah, dalam arti, yang sebaliknya. Kita perlu mengatur parameter sandwich dengan variabel acak, tidak memiliki data statistik, tetapi dipandu oleh sifat-sifat yang diperlukan dari jumlah ini. Ini adalah bagian yang penting dan menarik dari metode Monte Carlo, yang menjadi sandaran baik solusi maupun kebenarannya.

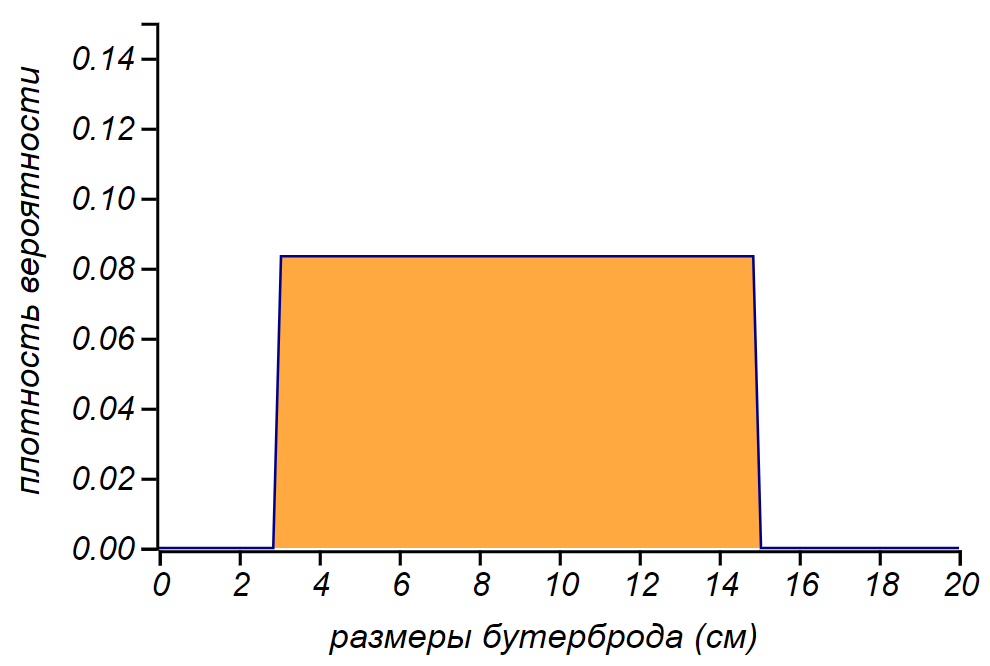1. Dimensi sandwich. Apa yang bisa mereka Canape berukuran wajar memiliki satu sentimeter $$$3$ lebar, dan "kulit pohon" siswa yang baik bisa menjadi sentimeter $$$15$ . Paling sering, sandwich memiliki ukuran $$$6$ sebelumnya $$$10$ lihat Dalam kasus ini, kemungkinan bertemu sandwich dengan lebar milimeter atau meter, dalam arti praktis, adalah nol. Saya tidak bisa mengatakan apa-apa lagi tentang sandwich dan saya akan menerima ukuran sandwich yang didistribusikan secara merata dalam rentang yang ditentukan. Pilihannya tidak sempurna, namun kami menemukan sandwich normal lebih sering daripada sandwich kecil atau raksasa. Tetapi nanti kita akan melihat bahwa titik lemah ini dapat dielakkan dengan anggun.

2. Posisi awal. Di sini, tanpa basa-basi lagi, kami akan mengatur distribusi seragam untuk memindahkan sandwich ke tepi meja, kalau saja jatuh.

3. Koefisien gesekan. Ini adalah jumlah yang tidak berdimensi, hanya bergantung pada bahannya. Meja dan taplak meja berbeda, jari meremas sandwich dengan kekuatan yang berbeda. Koefisien mulai dari $$$0,01$ sebelumnya $$$0,5$ , sementara nilai ekstrim tidak mungkin, secara rata-rata, Anda dapat mengharapkan sesuatu $$$0,3$ . Setiap distribusi asimetris berbentuk lonceng dari nilai non-negatif, misalnya, distribusi gamma atau log-normal, akan membantu kami.

4. Kecepatan awal. Kami jarang meluncurkan sandwich dengan kecepatan tinggi, dan paling sering kami tidak melemparnya sama sekali, tetapi hal itu memang terjadi. Semua yang diketahui tentang besarnya kecepatan adalah bahwa itu positif, dan dapat diasumsikan bahwa ketika menyapu, rata-rata kita bergerak dengan cara yang sama seperti tangan rata-rata, yaitu, dengan kecepatan sekitar $$$0,5$ m / s Jika hanya ini yang diketahui tentang kuantitas, maka masuk akal untuk menggambarkannya dengan distribusi eksponensial (mengapa, kita akan berbicara nanti ketika kita mengetahui tentang entropi distribusi). Modusnya nol, sehingga proporsi sandwich yang jatuh tanpa kecepatan awal yang besar akan cukup baik. Dalam "ekor" akan menjadi sandwich, secara tidak sengaja diluncurkan ke penerbangan ketika mengocok remah-remah dari meja.

5. Kami akan memperbaiki ketinggian meja, menjatuhkan seratus sandwich darinya, menghitung jumlah minyak yang jatuh ke bawah dan menaruhnya di atas meja, atau mencerminkan kemungkinan ketinggian pada grafik.

Berikut adalah probabilitas menjatuhkan sandwich dengan mentega ke bawah yang kita dapatkan:

Kemungkinan sandwich minyak mendarat sandwich berbeda dengan kondisi berbeda tergantung pada ketinggian musim gugur. Untuk setiap ketinggian $$$100$ tes.

Beberapa kecenderungan terlihat, tetapi penyebaran yang sangat luas telah terjadi. Ketika rata-rata, ternyata probabilitas ketinggian jatuh hampir independen dan hampir tidak melebihi setengahnya. Bisakah Anda memercayai eksperimen seperti itu? Apakah dia membantah hukum sandwich? Mungkin kita tidak cukup melempar sandwich - ada begitu banyak data berisik! Mari kita tambah jumlah lemparan dan lihat apa yang terjadi:

Probabilitas pendaratan minyak ke berbagai sandwich dihitung untuk jumlah tes yang lebih besar (500 untuk setiap ketinggian).

Ada lebih sedikit emisi, tetapi bahkan lebih jelas terlihat bahwa hukum sandwich sangat, sangat lemah. Tetapi apakah kami melakukan eksperimen dengan benar? Metode Monte Carlo terlihat sangat sederhana: ketahui diri Anda menggantikan data mengerikan apa dan lihat apa yang terjadi. Matematika adalah hal yang jujur: pertanyaan seperti apa yang siap dia berikan jawaban seperti apa . Tetapi apakah jawaban ini masuk akal tergantung pada pertanyaan.

Sebelum memulai eksperimen, tidak seperti mainan seperti milik kami, tetapi nyata dan mahal, menggunakan satelit yang mengorbit, akselerator partikel atau ribuan sandwich nyata dengan minyak, perlu untuk melakukan pekerjaan persiapan. Dan salah satu cara yang kuat dan indah untuk memahami bagaimana melakukan percobaan dengan benar adalah menganalisis dimensi masalah.

Kami memodelkan sandwich dengan koordinat umum, momen dan gaya - jumlah fisik, yang, pada gilirannya, dihubungkan oleh persamaan mekanika analitik. Dalam fisika, jumlah kuantitatif yang kita pakai, yang kita ukur dan gantikan dalam persamaan, tidak "cocok" dengan bilangan biasa - mereka memiliki struktur tambahan, yang disebut dimensi . Tidak semua ekspresi matematis yang benar masuk akal jika jumlah dimensi berpartisipasi di dalamnya. Katakanlah tidak masuk akal untuk menambah kecepatan dan massa, tidak mungkin untuk membandingkan kekuatan dan jarak. Namun, kita dapat mempertimbangkan produk kecepatan dan massa, setelah menerima kuantitas dimensi baru - momentum, atau momentum; adalah mungkin untuk mengkuadratkan kecepatan dan membaginya dengan jarak, sehingga memperoleh nilai yang memiliki dimensi akselerasi.

Analisis dimensi dan teori kesamaan lahir sejak lama, sejak zaman Lord Rayleigh. Mereka digunakan dalam mekanika, elektrodinamika, dalam astrofisika dan kosmologi, sehingga memungkinkan untuk melakukan tugas-tugas kompleks dengan keanggunan yang menakutkan. Namun, penelitian di bidang ini belum selesai dan definisi ketat dari struktur yang dibentuk oleh kuantitas kuantitatif (dimensi) hanya diberikan pada tahun 2016 oleh ahli matematika Spanyol Alvaro Raposo.

Kendala yang dipaksakan oleh dimensi pada formula fisik sering dianggap oleh siswa dan siswa sebagai kekacauan tambahan yang perlu dipantau. Tetapi di sisi lain, kendala yang konsisten secara logis sangat berguna! Mereka menyaring ekspresi yang salah, mereka memungkinkan Anda untuk "memprediksi" struktur solusi masalah fisik sebelum solusi terperinci, mereka adalah alat yang ampuh dalam merencanakan dan menganalisis data eksperimental.

Tapi itu menarik. Kami menghitung jatuhnya sandwich dalam program, menggunakan bukan angka tetapi angka biasa. Bagaimana seseorang bisa "menghapus" kuantitas fisik dari dimensi dan mengubahnya menjadi angka? Untuk tujuan ini, kita akrab dengan satuan pengukuran kuantitas fisik: semua meter, pound, menit, dan Newton ini. Unit pengukuran mengambil bagian dimensi dari kuantitas, meninggalkan kita dengan faktor - bilangan real, yang sudah dapat ditangani oleh komputer. Misalnya, kecepatan dalam arah yang dipilih adalah $$$60$ km / jam dapat direpresentasikan dengan angka $$$60$ . Tetapi ada kehalusan: representasi numerik tergantung pada pilihan satuan pengukuran. Jika Anda memilih unit lain (katakanlah, meter dan detik) , kecepatan yang sama akan diwakili oleh nomor yang berbeda: $$$16,7$ . Jumlahnya berbeda, tetapi jumlahnya adalah satu, dan itu tidak tergantung pada pilihan kami untuk setiap unit.

Timbul pertanyaan: apakah ada sistem unit yang “terbaik”? Ternyata ada, untuk ini, ketika memecahkan masalah, perlu untuk menggunakan jumlah dimensi yang dimasukkan dalam masalah sebagai unit pengukuran.

Dalam bab ini, kami memiliki sandwich yang terbang, dalam koin terbang sebelumnya, kami memberikan satu lagi contoh terbang. Bagaimana kualitas penerbangan burung yang berbeda dibandingkan? Jelas bahwa kecepatan yang dikembangkan burung berbeda: untuk merpati - $$$90$ km / jam, di jalan cepat - $$$140$ km / jam, untuk derek, burung pipit atau palu - $$$50$ km / jam, burung kolibri - $$$80$km / jam Tetapi semua burung ini sangat bervariasi dalam ukuran dan cara terbang. Jika panjang nuri diukur dalam nuri, dan waktu diukur dalam periode mengepakkan sayapnya, Anda bisa mendapatkan kecepatan sendiri , seperti yang mereka katakan . Anda dapat membagi kecepatan burung-burung ini dapat berkembang menjadi nilai eigen dan mendapatkan kecepatan tanpa dimensi yang menunjukkan berapa lama tubuh dapat melakukan perjalanan dalam satu kepakan sayap. Inilah hasil perbandingan ini:

burung	kecepatan, km / jam	panjang tubuh	frekuensi sapuan, 1 / s	kecepatan sendiri, m / s	kecepatan tanpa dimensi
cepat	140	18 cm	5	0,9	43
merpati pos	90	30 cm	5	1,5	17
burung kolibri	80	8 cm	200	16	1.4
crane	50	1 m	2,5	2,5	5
mallard	50	40 cm	9	3.6	3.8
burung gereja	46	12 cm	13	1,6	8

Dapat dilihat bahwa burung layang-layang dianggap selebaran terbaik, tetapi burung kolibri tidak efisien dalam mengkonsumsi energi, namun burung ini tidak memiliki tugas terbang untuk waktu yang lama, seperti burung merpati. Kecepatan absolut yang sama dari crane, sparrow dan bebek berbeda secara signifikan ketika diterjemahkan ke dalam jumlah yang tidak berdimensi. Perhitungan semacam ini digunakan untuk mensimulasikan pesawat nyata besar, menguji model kecil di terowongan angin. Jika semua parameter tanpa dimensi dari kedua sistem ini dekat, mereka dapat dianggap serupa secara fisik dan pemodelan masuk akal. Kami telah menggunakan pendekatan ini, mencerminkan unit relatif daripada yang absolut pada diagram Lorenz. Ini memungkinkan kami untuk membandingkan berbagai fenomena dan distribusi di antara mereka sendiri.

Jelaslah sistem unit apa yang paling cocok saat menganalisis penerbangan sandwich. Tentu saja, panjangnya harus diukur dalam sandwich. Untuk satuan waktu, kita dapat mengambil nilainya$$$\sqrt{l/g}$ dimana $$$l$ - panjang sandwich, dan $$$g$- percepatan gravitasi. Dan ketinggian meja tidak harus diukur dalam meter, tetapi dalam satuan sendiri. Dengan demikian memperoleh hasilnya, kita dapat segera menggeneralisasikannya baik untuk canape maupun ke "sepatu kulit" yang solid. Jadi, kami mengulangi perhitungan, tetapi pada grafik kami mencerminkan ketinggian tabel dalam satuan relatif. Jika kita melakukan segalanya dengan benar, maka untuk dua sandwich ukuran berbeda, kita harus mendapatkan gambar yang sangat mirip. Mari kita periksa ini:

Peluang sandwich sandwich mendarat pada nilai tetap tertentu, pada ketinggian insiden berbeda, dihitung dalam unit relatif. Titik biru sesuai dengan sandwich dengan ukuran 5 cm, titik merah sesuai dengan 10 cm.

Dalam formulasi awal, kami menyortir berbagai ukuran dan menerima awan hasil di mana ketergantungan yang menarik bagi kami disembunyikan. Dengan peningkatan jumlah tes, kami membuat rata-rata cloud ini dan menerima jawaban yang tidak menarik. Untuk lebih jelasnya menunjukkan kesalahan metodologis, bayangkan kita ingin menghitung kemungkinan sandwich jatuh, turun secara acak melihat kondisi awal dan ukuran sandwich dan tinggi. Ini setara dengan rata-rata semua hasil yang kami peroleh sekaligus. Sebagai hasilnya, kami mendapatkan jalan tengah yang percaya diri - kemungkinan yang sangat dekat$$$1/2$suka melempar koin! Ini adalah hasil yang sangat logis dan diharapkan, tetapi sama sekali tidak menarik. Dengan rata-rata banyak data untuk ukuran yang berbeda, kami sudah dekat dengan kesimpulan ini. Tetapi jika tujuan pemodelan adalah untuk mengidentifikasi pola, masuk akal untuk meminimalkan jumlah parameter.

Data yang telah dibersihkan sekarang jelas-jelas mendukung hukum kekejaman, namun membatasinya sampai batas tertentu: dari$$$2$ sebelumnya $$$6$ ukuran sandwich (dari ketinggian siku di atas meja ke ketinggian lengan orang yang berdiri). Di luar kisaran ini, sandwich memiliki peluang lebih tinggi untuk membalikkan sisi kanan sebelum jatuh.

Tetapi bagaimana jika Anda melihat lebih jauh dan melemparkan sandwich ke luar jendela? Jelas bahwa ketika jatuh dari ketinggian, tidak masalah dari sisi mana ia jatuh menjadi sandwich yang akan berubah, dan hambatan udara menstabilkan jatuh, tetapi secara teoritis, apa yang kita harapkan untuk dilihat? Mungkin, beberapa fluktuasi dalam probabilitas harus diamati ketika waktu penerbangan meningkat. Mari kita lihat:
Kemungkinan pendaratan sandwich minyak saat jatuh dari ketinggian.

Kami menebak dengan frekuensinya, tetapi aneh bahwa amplitudo menurun, dan fluktuasi probabilitas bertemu $$$0,5$ . Apa yang bisa dibicarakan? Apakah ini efek yang sama seperti dalam kasus koin, ketika dengan peningkatan durasi penerbangan konsekuensi penyimpangan kondisi awal menjadi lebih signifikan? Ternyata dalam hal ini sifat pemerataan probabilitas berbeda.

Analisis sedikit lebih dimensional

Tidak peduli seberapa serampangan topik buku kita, kita berbicara dalam bahasa matematika, dan dia berusaha mencari solusi yang tepat. Metode Monte Carlo memungkinkan kami untuk mendapatkan ide solusinya, tetapi itulah yang disebut brute force. Ini tidak semenarik setidaknya beberapa, tetapi solusi analitis. Analisis dimensi akan memungkinkan kita untuk mendapatkan bentuk teoretis dari ketergantungan yang diperoleh dengan metode Monte Carlo. Untuk ini, kita tidak perlu menyelesaikan persamaan diferensial, terlebih lagi, semua pertimbangan kita tidak melampaui batas hubungan yang sepenuhnya primitif dan jelas. Ini adalah pesona analisis dimensi, yang, bagaimanapun, terkadang terlihat seperti trik. Jadi mari kita mulai, membatasi diri kita sendiri demi kesederhanaan hanya dengan menyelipkan roti lapis panjang $$$l$ dari tabel ketinggian $$$H$ dengan nol kecepatan horisontal.

1. Sudut rotasi sandwich yang jatuh tergantung pada waktu dan kecepatan sudut:

$$

$$\ varphi = t \ omega.$$

2. Kecepatan sudut sama dengan produk dari waktu geser dan percepatan sudut:

$$

$$\ omega = t_0 \ varepsilon.$$

3. Waktu geser dapat dinyatakan dalam hal percepatan gravitasi dan bagian dari panjang sandwich yang bersentuhan dengan meja dalam proporsi berikut:

$$

$$t_0 \ propto \ sqrt {\ frac {l_0} {g}}.$$

Di sini $$$l_0$ - Panjang sandwich tergeletak di atas meja. Di sini kita menggunakan hubungan proporsionalitas yang ditunjukkan oleh tanda $$$\ propto$ . Ekspresi $$$y \ propto x$ dapat digantikan oleh $$$y = C x$ dimana $$$C$ - beberapa konstanta yang tidak diketahui. Saya sangat menyukai sikap ini. Proportionalitas "menggabungkan" segala sesuatu yang rumit yang berubah menjadi konstan: baik fakta bahwa momen gravitasi berubah selama rotasi, dan bahwa pusat rotasi berubah ketika meluncur. Semua ini, tentu saja, Anda perlu tahu untuk perhitungan yang akurat, tetapi hasilnya hanya koefisien tanpa dimensi, dan dalam analisis kami itu tidak berperan. Dengan satu ikon, kami menyelamatkan diri dari integrasi yang membosankan.

4. Akselerasi sudut terjadi dari percepatan gravitasi dan tergantung pada bahu yang diterapkan gravitasi:

$$

$$\ varepsilon \ propto \ frac {g} {l-l_0}.$$

Dan lagi tandanya $$$\ propto$ memungkinkan kita untuk tidak menghitung momen inersia lempeng untuk sumbu yang terletak di bidangnya, serta proyeksi perubahan gravitasi (ini adalah dua integral lagi).

5. Akhirnya, waktu jatuh tergantung pada ketinggian meja dan percepatan gravitasi:

$$

$$t \ propto \ sqrt {\ frac {H} {g}}.$$

6. Mengganti semua ekspresi ini dalam rumus pertama, kami memperoleh hasil sederhana:

$$

$$\ varphi \ propto \ sqrt {\ frac {l_0 H} {l (l-l_0)}},$$

yang, jika Anda mengukur semua panjang di sandwich, berubah menjadi

$$

$$\ varphi \ propto \ sqrt {\ frac {x h} {1-x}}.$$

Di sini $$$l_0 = x l$ dan $$$H = h l$ . Nah, semuanya bertemu - sudutnya tidak berdimensi dan itu tergantung pada koefisien tanpa dimensi. Sudut ini tidak tergantung pada skala waktu, geometri murni tetap. Penyebut tidak berbahaya saat $$$x> 0,5$ sandwich tidak akan jatuh sama sekali (kami sedang mempertimbangkan kecepatan nol horisontal), jadi $$$0 <x <0,5$ .

Sisi mana sandwich akan jatuh ditentukan oleh tanda sinus sudut $$$\ varphi$ mis. berfungsi $$$\ mathrm {sign} (\ sin \ varphi)$ . Fungsi ini kembali $$$-1$ untuk kasus "minyak" dan $$$1$ untuk "minyak turun." Kita dapat menggunakan fungsi ini untuk menyatakan kemungkinan jatuh sandwich deterministik jika kita membawanya ke kisaran $$$0$ sebelumnya $$$1$ :

$$

$$P _ {\ downarrow} (x, h) = \ frac12 \ kiri [1+ \ mathrm {sign} (\ sin \ varphi) \ kanan] = \ frac12 \ kiri \ {1+ \ mathrm {sign} \ kiri [ \ sin \ kiri (C \ sqrt {\ frac {xh} {1-x}} \ kanan) \ kanan] \ kanan \},$$

di mana panah menunjukkan posisi minyak secara simbolis. Koefisien $$$C$ yang muncul dalam rumus probabilitas mengekspresikan segala sesuatu yang tetap tersembunyi dengan bantuan tanda proporsional. Itu memang langkah yang sangat rumit, ini menyelamatkan kami dari integrasi yang membosankan (dan bahkan tiga), tetapi bagaimana kita sekarang mengetahui apa yang setara dengan koefisien ini? Selain itu, dari percobaan, satu percobaan tunggal dengan mengukur sudut pada saat jatuh sudah cukup untuk mendapatkan perkiraan nilai ini! Menggunakan simulator, saya dengan mudah menemukan itu $$$C = 2.3$ .

Tugas selanjutnya adalah mengekspresikan posisi awal secara matematis $$$x$ mungkin berbeda. Kami tertarik pada kemungkinan roti lapis akan jatuh jika $$$x$ akan sama $$$0,2$ atau $$$0,4$ atau nomor apa saja dari $$$0$ sebelumnya $$$0,5$ . Kami menggunakan serikat "atau", dan masing-masing kasus ini dianggap oleh kami sebagai independen dan mengecualikan semua yang lain dalam percobaan tertentu. Ingat bahwa probabilitas adalah ukuran ruang probabilitas, dan jika demikian, maka probabilitas adalah tambahan. Ini memungkinkan kita untuk menambahkan probabilitas $$$P _ {\ downarrow} (x, h)$ , untuk semua nilai $$$x$ , mengalikan dari sebelumnya dengan probabilitas jatuh ke rentang nilai tertentu. Kami memutuskan segmen dari $$$0$ sebelumnya $$$0,5$ pada $$$n$ bagian, dan menghitung estimasi probabilitas dalam bentuk jumlah:

$$

$$P _ {\ downarrow} (h) \ sim \ frac {2} {n} \ jumlah \ limit_ {i = 0} ^ n P _ {\ downarrow} \ kiri (\ frac {i} {2n}, h \ kanan ),$$

di sini adalah pengganda $$$2 / n$ menyatakan probabilitas untuk variabel acak $$$x$ masuk ke selembar lebar $$$1 / n$ . Ini adalah bagaimana hasilnya terlihat untuk sejumlah besar partisi ( $$$n = 100$ ) dan serangkaian eksperimen numerik dengan nol kecepatan horizontal:

Penilaian teoretis dan eksperimental tentang kemungkinan pendaratan minyak pada sandwich ketika jatuh dari ketinggian. Kecepatan horisontal awal dalam percobaan adalah nol.

Solusi yang kami sajikan sebelumnya mengandung lebih banyak parameter acak, sehingga ternyata lebih halus dan dekat $$$0,5$ . Tetapi, pada prinsipnya, analisis dimensi dapat dilakukan untuk kasus yang lebih umum.

Harap dicatat bahwa kemungkinannya $$$P _ {\ downarrow}$ mendekati dengan meningkatnya $$$h$ ke nilai yang dekat dengan $$$0,5$ . Dan ini sama sekali bukan karena ketidakpastian dan pengaruh kesalahan awal. Perhitungan menunjukkan bahwa ini adalah hasil dari penambahan banyak harmonisa yang dibentuk oleh nilai-nilai $$$x$ saat menjumlahkan $$$P _ {\ downarrow} (x, h)$ . Jika kita melupakan sandwich malang dan melanjutkan jadwal $$$P _ {\ downarrow}$ , maka kita melihat bahwa estimasi probabilitas akan terus berfluktuasi begitu dekat $$$0,5$ , secara bertahap berjuang untuk nilai ini.

Apakah mungkin untuk mencari tahu tanpa perhitungan langsung apakah probabilitas akan terus menyatu $$$0,5$ atau akankah ia tumbuh lagi? Dan dalam fenomena ini ada juga tempat untuk matematika non-sepele dan mendalam. Faktanya adalah bahwa setiap nilai $$$x$ frekuensi osilasi tertentu bersesuaian, dan seluruh rangkaian membentuk spektrum yang disebut fungsi total. Jika spektrum diskrit, yaitu terdiri dari frekuensi yang terpisah, maka fungsi total (disebut transformasi Fourier) akan periodik. Untuk spektrum berkelanjutan dalam bentuk konstanta pada segmen dari $$$0$ sebelumnya $$$0,5$ fungsi aperiodik yang berhubungan dengan berkurangnya osilasi akan sesuai. Tapi kami melihat ke cabang baru matematika - analisis fungsional .

Enrico Fermi yang hebat, kakek dari metode Monte Carlo (matematikawan Stanislav Ulam dianggap sebagai bapak), mengajar murid-muridnya untuk melakukan evaluasi sederhana, mencari selembar kertas atau jari, yang kita harapkan sebelum melanjutkan dengan solusi tepat untuk masalah tersebut. Sungguh luar biasa bahwa jika penilaian ternyata benar, maka akan menjadi jelas bahwa esensi masalah ditangkap, jika tidak, maka ini adalah hasil yang lebih berguna - itu berarti tugas tersebut ternyata lebih menarik daripada kelihatannya!

Dalam kasus kami, perkiraan sederhana sudah cukup, masalah sandwich tidak layak solusi yang lebih menyeluruh. Metode Monte Carlo menunjukkan kepada kita hanya petunjuk dari solusi, dan analisis dimensi hanya menunjukkan beberapa struktur umumnya, tetapi bersama-sama mereka dapat menunjukkan kepada kita bagaimana probabilitas yang diinginkan bekerja. Pengetahuan memungkinkan ahli matematika untuk melihat struktur yang sudah jadi dalam cetak biru dari solusi dan membuat asumsi dan kesimpulan yang luas.

Robert Matthews, dalam studi tengara, juga menggunakan analisis dimensi untuk menunjukkan bahwa hukum sandwich itu fundamental. Kesimpulannya didasarkan pada fakta bahwa ketinggian maksimum dari suatu organisme yang telah mencapai tungkai belakangnya dengan tujuan mengambil kaki depan untuk mengambil sandwich dengan minyak ditentukan oleh sifat kekuatan jaringan biologis dan gravitasi. Pada gilirannya, ukuran karakteristik sandwich harus sesuai dengan skala makhluk - dan kurcaci di beberapa planet berat dan dylds di planet dengan gravitasi rendah akan memilih sandwich untuk ukuran sendiri. Di sini kita sampai pada apa yang disebut spekulasi dalam sains. Ini bukan penjualan kembali barang apa pun dengan harga selangit, tetapi asumsi yang meragukan yang membentuk dasar dari konstruksi logis. Secara khusus, kami berasumsi bahwa makhluk memiliki tangan yang memiliki proporsi yang sama dengan tangan kita, dan ini lebih dari bisa diperdebatkan.

Tentang minyak dan angin

Dalam merfologi, kutipan yang salah dari hukum X.L. Grup Menka:

Masalah kompleks selalu memiliki solusi yang salah, sederhana, mudah dipahami, dan salah.

Anda sering dapat mendengar bahwa hukum roti lapis adalah yang harus disalahkan atas minyak, yang lebih padat dari pada roti dan karenanya “lebih penting daripada”. Dan meskipun ini tidak berlaku untuk subjek buku kami, saya ingin menganalisis pertanyaan ini untuk mengakhiri itu. Sehingga siapa pun nantinya dapat merujuk pada fakta bahwa "para ilmuwan telah membuktikan bahwa kehadiran minyak tidak memengaruhi sisi sandwich yang ditampar!"

Sebagai seorang anak, kami terhibur dengan melempar lalat merpati atau bulu ekor, terjebak dalam sepotong plastisin, berdiameter satu atau dua sentimeter, tinggi-tinggi. Itu terbang hingga empat meter, setelah itu turun dengan indah dan lancar di autorotation, seperti helikopter dengan mesin teredam. Lalu kami tumbuh dewasa, dan kesenangan kami menjadi tidak berbahaya. Kami mendapat mur dan memasang dua baut ke dalamnya dari sisi yang berlawanan, mengompresi isian dari kepala korek yang hancur. Tetap mengikat pita atau hanya seutas tali ke salah satu baut, benar-benar terlepas dan berlari ke langit selama lima belas meter. Pada musim gugur, pita cahaya menstabilkan posisi vertikal proyektil, memberikan dampak berkualitas tinggi pada aspal dan ledakan kecil, terkadang merobek mur menjadi potongan-potongan. (Hati-hati jika Anda memutuskan untuk membagikan pengalaman masa kecil ini dengan anak-anak Anda!)

Dalam kedua percobaan, kita melihat bahwa pena atau selotip dengan cepat muncul di bagian berat peralatan dan menstabilkan jatuh. Ini, tampaknya, mengarah pada pendapat intuitif bahwa mentega berat dan roti ringan juga harus berperilaku seperti ini. Bayangkan sebuah balon: keranjang yang lebih padat selalu terletak di bawah balon yang kurang padat. Selain itu, pengalaman menunjukkan bahwa jika Anda memegang dengan dua jari tengah geometris dari sebuah objek dengan massa yang terdistribusi secara asimetris, maka ia akan jatuh sehingga bagian yang berat berada di bagian bawah.

Tetapi kedua fenomena ini tidak bekerja dalam kasus sandwich yang jatuh.

Mari kita mulai dengan proses kedua - dengan "melebihi". Bukan kebetulan saya dengan bosannya menetapkan: "... jika Anda mengambil titik tengah geometris dari sebuah objek ..", itu berarti bahwa titik-titik singgung terletak pada garis lurus tertentu yang membentuk sumbu rotasi yang melewati pusat gravitasi objek. Dalam hal ini, memang, posisi stabil adalah posisi di mana pusat gravitasi berada di bawah sumbu. Tetapi jika sumbu rotasi yang dibentuk oleh jari-jari melewati pusat gravitasi, maka sistem akan berada dalam kesetimbangan acuh tak acuh - tidak akan peduli bagaimana itu diorientasikan.

Apa yang membuat bulu dengan bobot kecil, bom dari kacang, atau balon dengan balon di keranjang membuat Anda menavigasi dengan cara yang "benar"? Udara. Dia "memegang" benda-benda kita sehingga porosnya melintas di atas pusat gravitasi. Lebih tepatnya, aliran udara yang mendekat yang menciptakan gaya yang didistribusikan di atas area tubuh. Dan titik kondisional penerapan gaya ini akan terletak di dekat pusat geometris kuadrat gambar. Untuk membuatnya lebih jelas, kita akan menggambar gaya yang bekerja pada balon bersyarat, seperti pada benda dengan kerapatan yang tidak rata:

Kekuatan yang membawa balon ke posisi stabil.

Bagaimana dengan sandwich?

Pertama, jika kita "mematikan" udara, itu hanya akan jatuh. Dalam jatuh bebas, tubuh berputar tepat di sekitar pusat massa, sehingga tidak memiliki alasan untuk berputar dengan cara khusus. Seperti yang mereka katakan di sekolah: "Di lift yang jatuh, ketiadaan bobot diamati." Mentega di dalam sandwich sama tidak berbobotnya.

Minyak padat dapat mempengaruhi proses selip, ini akan secara efektif meningkatkan pusat massa di atas sentuhan yang tepat dan mengubah ekspresi untuk akselerasi sudut $$$l$ pada $$$\ sqrt {l ^ 2 + d ^ 2} = l \ sqrt {1+ \ delta ^ 2}$ dimana $$$\ delta = d / l$ - ketebalan relatif dari sandwich. Untuk nilai kecil $$$\ delta$ ungkapan ini dapat dihitung sebagai $$$l (1+ \ delta ^ 2/2)$ . Kami mendapatkan, seperti kata mereka, efek orde kedua. Untuk sandwich dengan rasio lebar terhadap ketebalan sama $$$5$ untuk $$$1$ , perubahan relatif tidak melebihi $$$2 \%$ . Dan ini adalah batas maksimum maksimum efek, karena kami menaikkan pusat massa ke ketebalan sandwich, yang sesuai dengan minyak padat tak terhingga!

Sekarang kita menghidupkan kembali udara, meninggalkan kerapatan minyak jauh lebih tinggi dari kerapatan roti. Kami memiliki pelat padat tipis dengan parasut ringan namun tahan udara. Sementara bidang sandwich horizontal atau lebih, momen hambatan udara sebanding dengan gerakan angin di atasnya - area di mana aliran udara berinteraksi: $$$M _ {-} \ propto l ^ 2$ . Dalam posisi tegak lurus, windage akan berkurang dan, karenanya, momennya akan berbeda: $$$M_ {|} \ propto l d$ . Rasio poin-poin ini: $$$M_ {|} / M _ {-} \ propto \ delta.$ Saya menulis tanda proporsional di sini, karena koefisien resistansi untuk pelat yang terletak di sepanjang dan di sepanjang aliran berbeda, dan mereka tidak diketahui oleh saya. Tetapi mereka tidak diperlukan - sudah jelas bahwa efek udara dalam posisi vertikal (yaitu, membuat posisi oli tidak merata) lebih lemah daripada di posisi horizontal. Dan sekarang kita ingat roti itu berputar, yang berarti roti itu diganti untuk alirannya, baik di ujung atau di pesawat. Kita bisa memperkenalkan tindakan pasukan perlawanan. Jika kecepatan sudut rotasi tidak berubah secara signifikan dalam satu periode (dan ini adalah kasus untuk udara), maka masuk akal untuk mengambil sebagai ukuran perubahan momentum sudut sebanding dengan waktu gaya. Pada gilirannya, periode tindakan sebanding dengan sudut "disapu" oleh sandwich selama periode ini. Akibatnya, langkah-langkah saat tindakan $$$M_ {|}$ dan $$$M _ {-}$ akan proporsional $$$M_ {|} \ varphi_ {|}$ dan $$$M _ {-} \ varphi _ {-}$ di mana sudut yang menyapu ujung dan bidang ditunjukkan pada gambar. 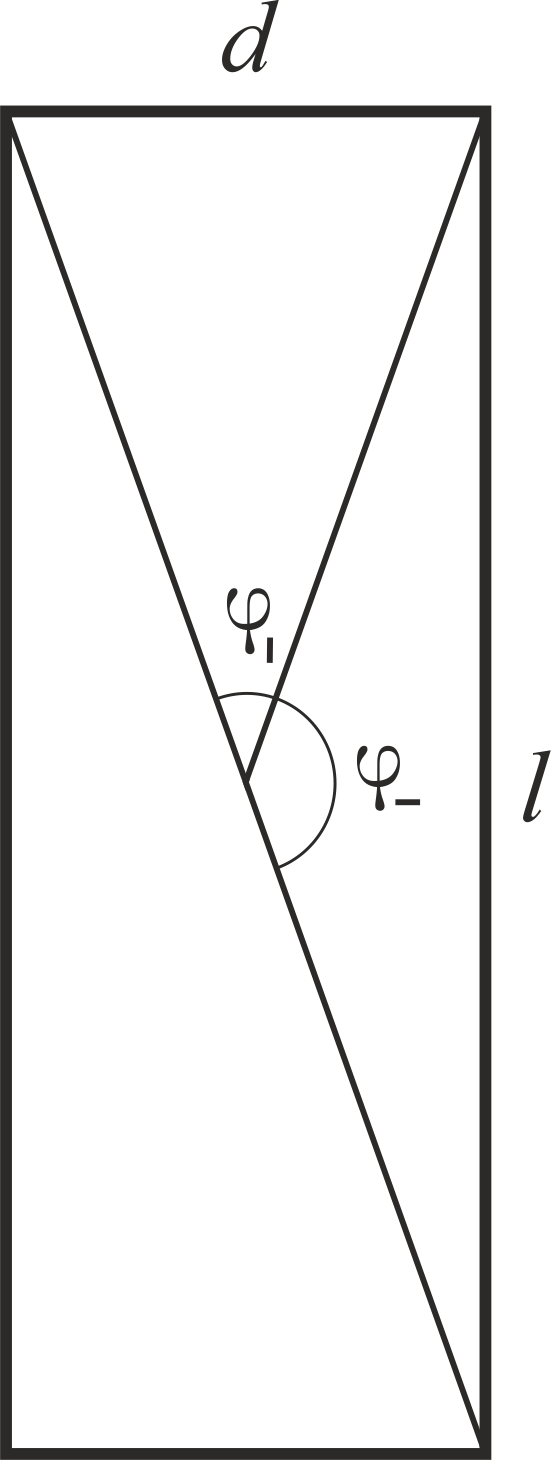Kita bisa menggunakan pekerjaan pasukan perlawanan sebagai ukuran dan mendapatkan rasio yang sama. Rasio sudut mudah dihitung:

$$

$$\ frac {\ varphi_ {|}} {\ varphi _ {-}} = \ frac {\ varphi_ {|}} {\ frac {\ pi} {2} - \ varphi_ {|}}.$$

Paling tidak $$$d / l$ , $$$\ varphi_ {|} \ sim \ delta$ (kami menggunakan properti garis singgung dari sudut kecil $$$10 \%$ akurasi pada sudut kurang $$$30 ^ \ circ$ ), dan oleh karena itu, kami memiliki:

$$

$$\ frac {M_ {|} \ varphi_ {|}} {M _ {-} \ varphi _ {-}} \ sim \ delta \ frac {\ delta} {\ frac {\ pi} {2} - \ delta} \ propto \ delta ^ 2.$$

Sekali lagi, ternyata efek asimetri untuk sandwich datar dibatasi oleh efek orde kedua. Biasanya, kepadatan mentega hanya dua kali lipat dari roti, dan pusat perpindahan massa tidak melebihi sepertiga dari ketebalan sandwich dengan lapisan mentega yang masuk akal tidak melebihi ketebalan roti. Pengamatan ini akan mengurangi efek minyak terhadap $$$0,2 \%$ .

Jika bagi pembaca tampaknya kita menembaki burung pipit dari pistol, maka saya sepenuhnya setuju dengannya. Tetapi, pertama, saya tidak ingin mendengar lebih banyak tentang minyak "melebihi", kedua, saya tidak ingin tidak berdasar, dan ketiga, saya ingin menunjukkan bagaimana fisikawan memperkirakan jumlah, mewakili proses, tetapi tidak memiliki data lengkap. Tentu saja, pada saat pendaratan, mentega dapat menempel ke lantai dan mencegah sandwich dari melompat dan menjungkirbalikkan lagi, tetapi saya pasti tidak akan membongkar mekanisme tumbukan, deformasi elastis dan lompatan sepotong roti. Jadi banyak analisis yang muncul untuk masalah ini. Dan Shnobelevskaya kedua untuknya tidak akan lagi diberikan.

$$

$$* * *$$

Tujuan dari jalan kita tidak begitu penting: sanggahan atau pembenaran hukum roti lapis, seperti jalan itu sendiri. Dia menunjukkan bagaimana kombinasi metode matematika yang berbeda memungkinkan Anda untuk melihat masalah dari sudut yang berbeda dan memberikan pengetahuan yang cukup akurat, bahkan tanpa solusi terperinci untuk masalah tersebut. Konsistensi dari berbagai disiplin ilmu matematika, pendekatan dan sudut pandang adalah kekuatan dan keindahan matematika. Sangat tepat untuk mengingat kata-kata indah dari Marina Tsvetaeva: "Saya tidak ingin memiliki sudut pandang, saya ingin memiliki penglihatan . " Studi tentang berbagai bidang matematika dapat memberi peneliti visi multidimensi "volumetrik" yang nyata, yang memungkinkan Anda untuk melihat ke dalam ruang pengetahuan yang tampaknya tertutup dan tersembunyi.