Mungkin, layanan apa pun yang umumnya memiliki pencarian, cepat atau lambat datang ke kebutuhan untuk belajar bagaimana memperbaiki kesalahan dalam permintaan pengguna. Errare humanum est; pengguna terus-menerus disegel dan salah, dan kualitas pencarian pasti menderita - dan dengan itu pengalaman pengguna.

Selain itu, setiap layanan memiliki spesifiknya sendiri, kosa katanya sendiri, yang harus dapat mengoperasikan pengoreksi kesalahan ketik, yang sangat mempersulit penggunaan solusi yang ada. Misalnya, permintaan tersebut harus belajar mengedit wali kami:



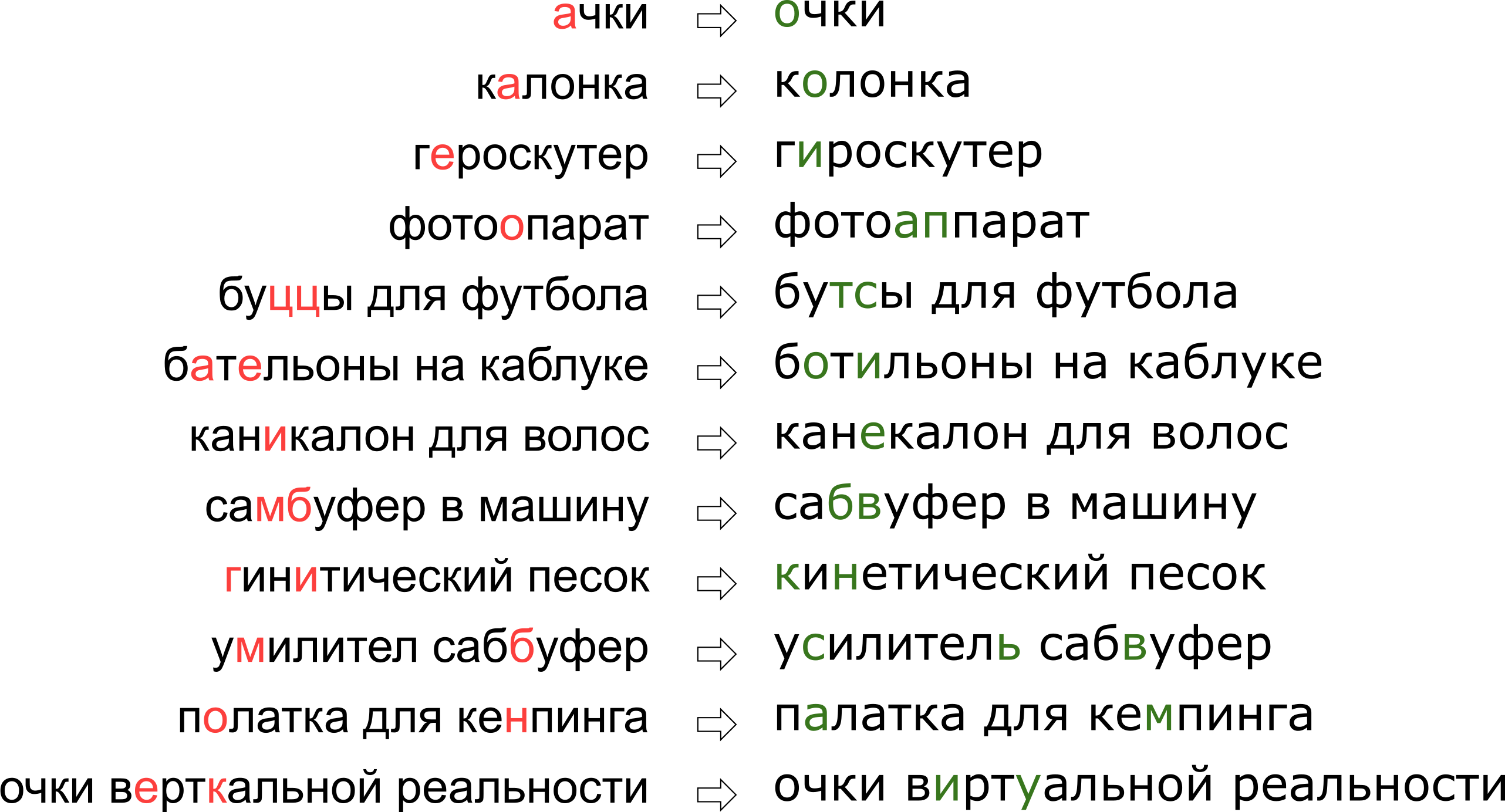Tampaknya kami menolak impian pengguna tentang realitas vertikal, tetapi sebenarnya huruf K hanya berdiri di keyboard di sebelah huruf U.

Pada artikel ini, kita akan melihat salah satu pendekatan klasik untuk memperbaiki kesalahan ketik, dari membangun model hingga menulis kode dengan Python dan Go. Dan sebagai bonus - video dari laporan saya " Kacamata Realitas Vertikal": kami mengoreksi kesalahan ketik dalam permintaan pencarian "di Highload ++.

Pernyataan masalah

Jadi, kami menerima permintaan yang disegel dan kami harus memperbaikinya. Biasanya, masalahnya secara matematis diajukan sebagai berikut:

• diberi kata $$$s$ dikirimkan kepada kami dengan kesalahan;
• punya kamus $$$\ Sigma$ kata-kata yang tepat;
• untuk semua kata w dalam kamus ada kemungkinan bersyarat $$$P (w | s)$ apa yang dimaksud dengan kata itu $$$w$ asalkan kita mendapat kata $$$s$ ;
• Anda perlu menemukan kata w dari kamus dengan probabilitas maksimum $$$P (w | s)$ .

Pernyataan ini - yang paling dasar - menunjukkan bahwa jika kami menerima permintaan beberapa kata, maka kami mengoreksi setiap kata secara terpisah. Pada kenyataannya, tentu saja, kita akan ingin mengoreksi seluruh frasa sebagai keseluruhan, mengingat kecocokan kata-kata yang berdekatan; Saya akan membicarakan hal ini nanti di bagian "Cara mengoreksi frasa".

Ada dua momen yang tidak jelas - di mana mendapatkan kamus dan bagaimana cara menghitung $$$P (w | s)$ . Pertanyaan pertama dianggap sederhana. Pada 1990 [1], kamus disusun dari basis data utilitas ejaan dan kamus yang tersedia secara elektronik; pada tahun 2009, Google [4] melakukan lebih sederhana dan hanya mengambil kata-kata paling populer di Internet (bersama dengan salah ejaan populer). Saya mengambil pendekatan ini untuk membangun wali saya.

Pertanyaan kedua lebih rumit. Kalau saja karena keputusannya biasanya dimulai dengan penerapan formula Bayes!

$$

$$P (w | s) = \ mathrm {const} \ cdot P (s | w) \ cdot P (w)$$

Sekarang, alih-alih probabilitas awal yang tidak dapat dipahami, kita perlu mengevaluasi dua yang baru, yang sedikit lebih dapat dipahami: $$$P (s | w)$ - probabilitas saat mengetik kata $$$w$ dapat disegel dan dapatkan $$$s$ , dan $$$P (w)$ - pada prinsipnya, probabilitas pengguna menggunakan kata tersebut $$$w$ .

Bagaimana cara menilai $$$P (s | w)$ ? Jelas, pengguna lebih cenderung membingungkan A dengan O daripada b dengan S. Dan jika kita memperbaiki teks yang dikenali dari dokumen yang dipindai, maka ada kemungkinan besar kebingungan antara rn dan m. Dengan satu atau lain cara, kita membutuhkan semacam model yang menjelaskan kesalahan dan probabilitasnya.

Model seperti itu disebut model saluran bising (model saluran bising; dalam kasus kami, saluran bising dimulai di suatu tempat di tengah Brock pengguna dan berakhir di sisi lain keyboard-nya) atau, lebih singkat, model kesalahan adalah model kesalahan. Model ini, yang dibahas pada bagian terpisah di bawah, akan bertanggung jawab untuk memperhitungkan kesalahan pengejaan dan, bahkan, kesalahan ketik.

Nilai probabilitas menggunakan kata - $$$P (w)$ - itu mungkin dengan cara yang berbeda. Pilihan paling sederhana adalah dengan mengambil frekuensi kata tersebut muncul di beberapa kumpulan teks besar. Bagi wali kita, dengan mempertimbangkan konteks frasa, tentu saja, sesuatu yang lebih rumit diperlukan - model lain. Model ini disebut model bahasa, model bahasa.

Model kesalahan

Model kesalahan pertama dipertimbangkan $$$P (s | w)$ , menghitung probabilitas substitusi dasar dalam set pelatihan: berapa kali alih-alih E yang mereka tulis DAN, berapa kali alih-alih T mereka menulis T, bukan T-T dan seterusnya [1]. Hasilnya adalah model dengan sejumlah kecil parameter yang dapat mempelajari beberapa efek lokal (misalnya, bahwa orang sering membingungkan E dan I).

Dalam penelitian kami, kami menetapkan model kesalahan yang lebih berkembang yang diusulkan pada tahun 2000 oleh Brill dan Moore [2] dan digunakan kembali nanti (misalnya, oleh para ahli Google [4]). Bayangkan bahwa pengguna tidak berpikir dalam karakter yang terpisah (membingungkan E dan I, tekan K bukan Y, lewati tanda lunak), tetapi dapat mengubah potongan kata yang berubah-ubah menjadi kata lain - misalnya, ganti TSYA dengan TYSYA, Y dengan K, SHA dengan SHCHYA, SS ke C dan seterusnya. Probabilitas bahwa pengguna disegel dan bukannya TSYA telah menulis THY, kami tunjukkan $$$P (\ text {ribu} \ rightarrow \ text {ribu})$ Merupakan parameter dari model kami. Jika untuk semua kemungkinan fragmen $$$\ alpha, \ beta$ kita bisa menghitung $$$P (\ alpha \ rightarrow \ beta)$ , maka probabilitas yang diinginkan $$$P (s | w)$ satu set kata s ketika mencoba mengetik kata w dalam model Brill dan Moore dapat diperoleh sebagai berikut: kita memecah kata w dan s menjadi fragmen yang lebih pendek dengan semua cara yang mungkin sehingga ada jumlah fragmen yang sama dalam dua kata. Untuk setiap partisi, kami menghitung produk dari probabilitas semua fragmen untuk berubah menjadi fragmen yang sesuai. Maksimum untuk semua partisi tersebut akan dianggap sebagai nilai $$$P (s | w)$ :

$$

$$P (s | w) = \ max_ {s = \ alpha_1 \ alpha_2 \ ldots \ alpha_k, w = \ beta_1 \ beta_2 \ ldots \ beta_k} P (\ alpha_1 \ rightarrow \ beta_1) \ cdot P (\ alpha_2 \ rightarrow \ beta_2) \ cdot \ ldots \ cdot P (\ alpha_k \ rightarrow \ beta_k) \,$$

Mari kita lihat contoh partisi yang terjadi ketika menghitung probabilitas pencetakan "aksesori" daripada "aksesori":

$$

$$\ begin {matrix} \ text {ak} & \ text {cec} & \ text {sou} & \ text {a} & \ text {p} \\ \ downarrow & \ downarrow & \ downarrow & \ downarrow & \ downarrow \\ \ text {a} & \ text {cc} & \ text {e} & \ text {soua} & \ text {p} \ end {matrix}$$

Seperti yang mungkin Anda perhatikan, ini adalah contoh dari partisi yang tidak terlalu sukses: jelas bahwa sebagian dari kata-kata tersebut tidak terletak di bawah satu sama lain sesukses mungkin. Jika jumlahnya $$$P (\ text {ak} \ rightarrow \ text {a})$ dan $$$P (\ text {p} \ rightarrow \ text {p})$ masih tidak terlalu buruk kalau begitu $$$P (\ text {sou} \ rightarrow \ text {e})$ dan $$$P (\ text {a} \ rightarrow \ text {soua})$ kemungkinan besar mereka akan membuat "skor" terakhir dari partisi ini benar-benar menyedihkan. Partisi yang lebih sukses terlihat seperti ini:

$$

$$\ begin {matrix} \ text {ak} & \ text {ce} & \ text {ss} & \ text {y} & \ text {ar} \\ \ downarrow & \ downarrow & \ downarrow & \ downarrow & \ downarrow \\ \ text {ak} & \ text {ce} & \ text {c} & \ text {y} & \ text {ar} \ end {matrix}$$

Di sini, semuanya langsung jatuh ke tempatnya, dan jelaslah bahwa probabilitas akhir akan ditentukan terutama oleh nilainya $$$P (\ text {ss} \ rightarrow \ text {s})$ .

Cara menghitung $$$P (s | w)$

Terlepas dari kenyataan bahwa ada perintah kemungkinan partisi untuk dua kata $$$O (2 ^ {| s | + | w |})$ menggunakan algoritma perhitungan pemrograman dinamis $$$P (s | w)$ dapat dibuat cukup cepat - untuk $$$O (| s | ^ 2 | w | ^ 2)$ . Algoritme itu sendiri akan sangat menyerupai algoritma Wagner-Fisher untuk menghitung jarak Levenshtein .

Kami akan membuat tabel persegi panjang, baris yang akan sesuai dengan huruf dari kata yang benar, dan kolom ke yang disegel. Sel di persimpangan baris i dan kolom j pada akhir algoritma akan memiliki probabilitas yang tepat untuk mendapatkan s[:j] ketika mencoba mencetak w[:i] . Untuk menghitungnya, cukup untuk menghitung nilai semua sel di baris dan kolom sebelumnya dan mengatasinya, mengalikan dengan yang sesuai $$$P (\ alpha \ rightarrow \ beta)$ . Sebagai contoh, jika kita memiliki tabel yang diisi


, lalu untuk mengisi sel di baris keempat dan kolom ketiga (abu-abu) Anda harus mengambil maksimum $$$0,8 \ cdot P (\ text {cc} \ rightarrow \ text {c})$ dan $$$0,16 \ cdot P (\ text {c} \ rightarrow \ text {k})$ . Pada saat yang sama, kami menjalankan semua sel yang disorot dalam gambar hijau. Jika kami juga mempertimbangkan modifikasi formulir $$$P (\ alpha \ rightarrow \ text {empty line})$ dan $$$P (\ text {empty line} \ rightarrow \ beta)$ , maka Anda harus memeriksa sel yang disorot dengan warna kuning.

Kompleksitas dari algoritma ini, seperti yang saya sebutkan di atas, adalah $$$O (| s | ^ 2 | w | ^ 2)$ : kita isi tabel $$$| s | \ kali | w |$ , dan untuk mengisi sel (i, j) yang Anda butuhkan $$$O (i \ cdot j)$ operasi. Namun, jika kami membatasi pertimbangan kami untuk fragmen tidak lebih dari beberapa panjang terbatas $$$L$ (misalnya, tidak lebih dari dua huruf, seperti pada [4]), kompleksitasnya akan berkurang menjadi $$$O (| s | \ cdot | w | \ cdot L ^ 2)$ . Untuk bahasa Rusia dalam percobaan saya, saya mengambil $$$L = 3$ .

Cara memaksimalkan $$$P (s | w)$

Kami belajar menemukan $$$P (s | w)$ untuk waktu polinomial baik. Tetapi kita perlu belajar cara cepat menemukan kata-kata terbaik di seluruh kamus. Dan yang terbaik bukan $$$P (s | w)$ tapi $$$P (w | s)$ ! Faktanya, cukup bagi kami untuk mendapatkan beberapa kata yang masuk akal (misalnya, 20 kata terbaik) untuk $$$P (s | w)$ , yang kemudian akan kami kirim ke model bahasa untuk memilih koreksi yang paling tepat (lebih lanjut tentang ini di bawah).

Untuk mempelajari cara menelusuri seluruh kamus dengan cepat, kami perhatikan bahwa tabel yang disajikan di atas memiliki banyak kesamaan untuk dua kata dengan awalan yang sama. Memang, jika kita, mengoreksi kata "aksesori", cobalah mengisinya untuk dua kata kosakata "aksesori" dan "aksesori", kita akan melihat bahwa sembilan baris pertama di dalamnya tidak berbeda sama sekali! Jika kita dapat mengatur pass kamus sehingga dua kata berikutnya memiliki awalan umum yang cukup panjang, kita dapat menyimpan banyak perhitungan.

Dan kita bisa. Mari kita ambil kata-kata kosa kata dan membuatnya trie . Berjalan melaluinya secara mendalam, kita mendapatkan properti yang diinginkan: sebagian besar langkah adalah langkah-langkah dari node ke turunannya, ketika tabel perlu mengisi beberapa baris terakhir.

Algoritma ini, dengan beberapa optimasi tambahan, memungkinkan kita untuk memilah kamus dari bahasa Eropa yang khas dalam 50-100 ribu kata dalam seratus milidetik [2]. Dan hasil caching akan membuat proses lebih cepat.

Bagaimana cara mendapatkannya $$$P (\ alpha \ rightarrow \ beta)$

Perhitungan $$$P (\ alpha \ rightarrow \ beta)$ untuk semua fragmen yang dipertimbangkan - bagian yang paling menarik dan non-sepele dari membangun model kesalahan. Dari jumlah inilah kualitasnya akan bergantung.

Pendekatan yang digunakan dalam [2, 4] relatif sederhana. Mari temukan banyak pasangan $$$(s_i, w_i)$ dimana $$$w_i$ Adalah kata yang benar dari kamus, dan $$$s_i$ - versi yang disegel. (Bagaimana tepatnya menemukan mereka sedikit lebih rendah.) Sekarang kita perlu mengekstrak probabilitas kesalahan ketik tertentu dari pasangan ini (mengganti beberapa fragmen dengan yang lain).

Untuk setiap pasangan kami mengambil komponennya $$$w$ dan $$$s$ dan membangun korespondensi antara surat-surat mereka, meminimalkan jarak Levenshtein:

$$

$$\ begin {matrix} \ text {a} & \ text {c} & \ text {c} & \ text {e} & \ text {c} & \ text {c} & \ text {y} & \ text {a} & \ text {p} \\ \ text {a} & \ text {k} & \ text {c} & \ text {e} & \ text {c} & \ text {} & \ text {y } & \ text {a} & \ text {p} \ end {matrix}$$

Sekarang kita segera melihat substitusi: a → a, e → dan, c → c, c → string kosong dan sebagainya. Kita juga melihat penggantian dua atau lebih karakter: ak → ak, ce → si, ec → is, ss → s, ses → sis, ess → is dan lainnya, dan seterusnya. Semua penggantian ini harus dihitung, dan masing-masing sebanyak kata s muncul dalam corpus (jika kita mengambil kata-kata dari corpus, yang sangat mungkin).

Setelah melewati semua pasangan $$$(s_i, w_i)$ untuk probabilitas $$$P (\ alpha \ rightarrow \ beta)$ jumlah substitusi α → β yang terjadi pada pasangan kami diterima (dengan mempertimbangkan terjadinya kata-kata yang sesuai) dibagi dengan jumlah pengulangan fragmen α.

Bagaimana menemukan pasangan $$$(s_i, w_i)$ ? Dalam [4], pendekatan ini diusulkan. Ambil konten besar yang dibuat pengguna (UGC). Dalam kasus Google, itu hanya teks-teks dari ratusan juta halaman web; Kami memiliki jutaan pencarian dan ulasan pengguna. Diasumsikan bahwa biasanya kata yang tepat lebih sering ditemukan di corpus daripada varian yang salah. Jadi, mari kita cari kata-kata untuk setiap kata yang dekat dengannya dari Levenshtein dari corpus, yang jauh kurang populer (misalnya, sepuluh kali). Jadilah populer $$$w$ , kurang populer - untuk $$$s$ . Jadi kita mendapatkan pasangan yang berisik, tetapi cukup besar untuk berlatih.

Algoritma pencocokan pasangan ini menyisakan banyak ruang untuk perbaikan. Dalam [4], hanya filter berdasarkan kejadian ( $$$w$ sepuluh kali lebih populer daripada $$$s$ ), tetapi penulis artikel ini mencoba membuat gosip, tanpa menggunakan pengetahuan apriori tentang bahasa tersebut. Jika kita hanya mempertimbangkan bahasa Rusia, kita dapat, misalnya, mengambil satu set kamus bentuk kata Rusia dan hanya menyisakan pasangan dengan kata $$$w$ ditemukan dalam kamus (bukan ide yang baik, karena kamus kemungkinan besar tidak memiliki kosakata khusus untuk layanan) atau, sebaliknya, buang pasangan dengan kata s yang ditemukan dalam kamus (artinya, hampir dijamin tidak akan disegel).

Untuk meningkatkan kualitas pasangan yang diterima, saya menulis fungsi sederhana yang menentukan apakah pengguna menggunakan dua kata sebagai sinonim. Logikanya sederhana: jika kata-kata w dan s sering ditemukan dikelilingi oleh kata-kata yang sama, maka mereka mungkin sinonim - yang, mengingat kedekatannya menurut Levenshtein, berarti bahwa kata yang kurang populer kemungkinan besar merupakan versi keliru dari yang lebih populer. Untuk perhitungan ini, saya menggunakan statistik tentang kemunculan trigram (frasa tiga kata) yang dibangun untuk model bahasa di bawah ini.

Model bahasa

Jadi, sekarang untuk kata kamus yang diberikan, kita perlu menghitung $$$P (w)$ - probabilitas penggunaannya oleh pengguna. Solusi paling sederhana adalah dengan mengambil kata dalam beberapa kasus besar. Secara umum, mungkin, model bahasa apa pun dimulai dengan mengumpulkan kumpulan besar teks dan menghitung kemunculan kata-kata di dalamnya. Tetapi kita tidak boleh membatasi diri kita pada hal ini: pada kenyataannya, ketika menghitung P (w), kita juga dapat memperhitungkan frasa di mana kita berusaha untuk mengoreksi kata, dan konteks eksternal lainnya. Tugas berubah menjadi tugas perhitungan $$$P (w_1w_2 \ ldots w_k)$ dimana salah satunya $$$w_i$ - kata di mana kita memperbaiki kesalahan ketik dan yang sekarang kita hitung $$$P (w)$ dan sisanya $$$w_i$ - Kata-kata yang mengelilingi kata yang diperbaiki dalam permintaan pengguna.

Untuk mempelajari cara memperhitungkannya, ada baiknya menelusuri korpus lagi dan menyusun statistik n-gram, urutan kata. Biasanya mengambil urutan panjang yang terbatas; Saya membatasi diri pada trigram agar tidak mengembang indeks, tetapi semuanya tergantung pada kekuatan pikiran Anda (dan ukuran kasing - pada kasing kecil bahkan statistik pada trigram akan terlalu berisik).

Model bahasa n-gram tradisional terlihat seperti ini. Untuk frasa $$$w_1w_2 \ ldots w_k$ probabilitasnya dihitung dengan rumus

$$

$$P (w_1w_2 \ ldots w_k) = P (w_1) \ cdot P (w_2 | w_1) \ cdot P (w_3 | w_1w_2) P (w_k | w_1w_2w_ {k-1}) \ ,,$$

dimana $$$P (w_1)$ - secara langsung frekuensi kata, dan $$$P (w_3 | w_1w_2)$ - probabilitas kata $$$w_3$ asalkan sebelum dia pergi $$$w_1w_2$ - hanya rasio frekuensi trigram $$$w_1 w_2 w_3$ ke frekuensi bigram $$$w_1 w_2$ . (Perhatikan bahwa formula ini hanyalah hasil dari penggunaan berulang formula Bayes.)

Dengan kata lain, jika kita ingin menghitung $$$P (\ text {bingkai sabun ibu})$ , yang menunjukkan frekuensi n-gram dalam $$$f$ kami mendapatkan formula

$$

$$P (\ text {mom soap frame}) = f (\ text {mom}) \ cdot \ frac {f (\ text {mom soap})} {f (\ text {mom})} \ cdot \ frac { f (\ teks {bingkai sabun ibu})} {f (\ teks {sabun ibu})} = f (\ teks {bingkai sabun ibu}) \,.$$

Apakah ini logis? Masuk akal. Namun, kesulitan dimulai ketika frasa menjadi lebih panjang. Bagaimana jika pengguna memasukkan permintaan pencarian sepuluh kata dengan detail yang mengesankan? Kami tidak ingin menyimpan statistik untuk semua 10 gram - ini mahal, dan datanya cenderung berisik dan bukan indikatif. Kami ingin bertahan dengan n-gram dengan panjang terbatas - misalnya, panjang 3 sudah diusulkan di atas.

Di sinilah rumus di atas berguna. Mari kita asumsikan bahwa probabilitas sebuah kata yang muncul di akhir kalimat secara signifikan dipengaruhi hanya oleh beberapa kata di depannya, yaitu,

$$

$$P (w_k | w_1w_2 \ ldots w_ {k-1}) \ approx P (w_k | w_ {k-L + 1} \ ldots w_ {k-1}) \,.$$

Puting $$$L = 3$ , untuk frasa yang lebih panjang kita mendapatkan formula


$$$P (\ text {carl mencuri karang dari Clara}) \ approx f (\ text {carl}) \ cdot \ frac {f (\ text {carl})} {f (\ text {carl})} \ cdot \ frac {f (\ text {carl from clara})} {f (\ text {carl from})} \ cdot \ frac {f (\ text {stole from clara})} {f (\ text {from clara} )} \ cdot \ frac {f (\ text {claire stole coral})} {f (\ text {claire stole})} \,.$


Harap dicatat: frasa terdiri dari lima kata, tetapi n-gram tidak lebih dari tiga muncul dalam rumus. Inilah yang kami cari.

Ada satu momen tipis yang tersisa. Bagaimana jika pengguna memasukkan frasa yang sangat aneh dan n-gram yang sesuai dalam statistik kami dan tidak sama sekali? Akan mudah bagi n-gram yang tidak dikenal untuk diletakkan $$$f = 0$ jika tidak perlu dibagi dengan nilai ini. Di sinilah bantuan perataan (smoothing), yang dapat dilakukan dengan berbagai cara; Namun, diskusi rinci tentang pendekatan anti-aliasing yang serius seperti perataan Kneser-Ney jauh di luar cakupan artikel ini.

Bagaimana cara mengoreksi frasa

Kami membahas titik halus terakhir sebelum beralih ke implementasi. Pernyataan masalah yang saya jelaskan di atas menyiratkan bahwa ada satu kata dan itu perlu diperbaiki. Kemudian kami mengklarifikasi bahwa satu kata ini mungkin ada di tengah frasa di antara beberapa kata lain dan mereka juga perlu diperhitungkan, memilih koreksi terbaik. Namun pada kenyataannya, pengguna hanya mengirim kami frasa tanpa menentukan kata mana yang dieja; sering beberapa kata atau bahkan semua perlu diperbaiki.

Mungkin ada banyak pendekatan. Misalnya, Anda dapat mempertimbangkan hanya konteks kiri kata dalam frasa. Kemudian, sesuai dengan kata-kata dari kiri ke kanan dan memperbaikinya seperlunya, kita akan mendapatkan frase baru dengan kualitas tertentu. Kualitasnya akan buruk jika, misalnya, kata pertama ternyata seperti beberapa kata populer dan kami memilih opsi yang salah. Seluruh frasa yang tersisa (mungkin awalnya benar-benar bebas kesalahan) akan disesuaikan oleh kami dengan kata pertama yang salah dan kami bisa mendapatkan teks yang sama sekali tidak relevan dengan aslinya.

Anda dapat mempertimbangkan kata-kata secara individual dan menerapkan pengelompokan tertentu untuk memahami apakah kata yang diberikan disegel atau tidak, seperti yang disarankan dalam [4]. Pengklasifikasi dilatih tentang probabilitas yang telah kita ketahui cara menghitung, dan sejumlah fitur lainnya. Jika classifier mengatakan apa yang perlu diperbaiki, kami memperbaikinya, mengingat konteks yang ada. Sekali lagi, jika beberapa kata salah dieja, Anda harus membuat keputusan tentang yang pertama berdasarkan konteks dengan kesalahan, yang dapat menyebabkan masalah kualitas.

Dalam implementasi wali kami, kami menggunakan pendekatan ini. Mari untuk setiap kata $$$s_i$ dalam frasa kami, dengan menggunakan model kesalahan kami menemukan kata-kata kamus top-N yang dapat berarti, kami menggabungkannya ke dalam frasa dengan segala cara yang mungkin dan untuk masing-masing $$$N ^ K$ frase yang dihasilkan di mana $$$K$ - jumlah kata dalam frasa asli, dengan jujur ​​menghitung nilainya

$$

$$P (s_1 | w_1) \ cdot P (s_K | w_K) \ cdot P (s_K | w_K) \ cdot P (w_1w_2 \ ldots w_K) ^ {\ lambda} \,.$$

Di sini $$$s_i$ - kata-kata yang dimasukkan oleh pengguna, $$$w_i$ - koreksi yang dipilih untuk mereka (yang sekarang kita selidiki), dan $$$\ lambda$ - koefisien ditentukan oleh kualitas komparatif dari model kesalahan dan model bahasa (koefisien besar - kami lebih mempercayai model bahasa, koefisien kecil - kami lebih mempercayai model kesalahan), diusulkan dalam [4]. Secara total, untuk setiap frasa, kami mengalikan probabilitas setiap kata untuk dikoreksi dalam varian kamus yang sesuai, dan kami juga mengalikannya dengan probabilitas seluruh frasa dalam bahasa kami. Hasil algoritma adalah frasa dari kata-kata kamus yang memaksimalkan nilai ini.

Jadi hentikan apa? Kekuatan kasar $$$N ^ K$ frasa?

Untungnya, karena kami telah membatasi panjang n-gram, mungkin untuk menemukan maksimum dalam semua frasa lebih cepat. Ingat: di atas kami menyederhanakan formula untuk $$$P (w_1w_2 \ ldots w_K)$ sehingga mulai bergantung hanya pada frekuensi panjang n-gram yang tidak lebih tinggi dari tiga:

$$

$$P (w_1w_2 \ ldots w_K) = P (w_1) \ cdot P (w_2 | w_1) \ cdot P (w_3 | w_1w_2) \ cdot \ ldots \ cdot P (w_K | w_ {K-2} w_ {K-1} }) \,.$$

Jika kita kalikan nilai ini dengan $$$P (s_i | w_i)$ dan coba maksimalkan dengan $$$w_K$ , kita akan melihat bahwa itu sudah cukup untuk memilah semua jenis $$$w_ {K-2}$ dan $$$w_ {K-1}$ dan memecahkan masalah bagi mereka - yaitu, untuk frasa $$$w_1w_2 \ ldots w_ {K-2} w_ {K-1}$ . Secara total, masalah diselesaikan dengan pemrograman dinamis di $$$O (KN ^ 3)$ .

Implementasi

Menyatukan case dan menghitung n-gram

Saya akan segera melakukan reservasi: tidak ada begitu banyak data yang saya miliki untuk memulai beberapa MapReduce yang kompleks. Jadi saya hanya mengumpulkan semua teks ulasan, komentar, dan permintaan pencarian dalam bahasa Rusia (deskripsi barang, sayangnya, datang dalam bahasa Inggris, dan penggunaan hasil terjemahan otomatis agak memburuk daripada memperbaiki hasil) dari layanan kami menjadi satu file teks dan mengatur server untuk malam menghitung. trigram dengan skrip Python sederhana.

Sebagai kamus, saya sering mengambil kata-kata teratas sehingga saya mendapatkan sekitar seratus ribu kata. Kata-kata yang terlalu panjang (lebih dari 20 karakter) dan terlalu pendek (kurang dari tiga karakter, kecuali kata-kata Rusia yang dikenal dengan hardcod) dikecualikan. Secara terpisah terhindar dari kata-kata pada keteraturan r"^[a-z0-9]{2}$" - sehingga versi iPhone dan pengenal menarik lainnya dengan panjang 2 bertahan.

Saat menghitung bigrams dan trigram dalam frasa, kata yang bukan kamus dapat muncul. Dalam hal ini, saya membuang kata ini dan mengalahkan seluruh frasa menjadi dua bagian (sebelum dan sesudah kata ini), yang dengannya saya bekerja secara terpisah. Jadi, untuk frasa " Tahukah Anda apa" abyrvalg "itu? Ini adalah ... THE HEADMAN, kolega "akan memperhitungkan trigram" Apakah Anda tahu, "" Anda tahu apa, "" tahu apa itu "dan" ini adalah kolega nelayan utama "(kecuali, tentu saja, kata" kepala "masuk ke dalam kamus ...).

Kami melatih model kesalahan

Selanjutnya saya melakukan semua pemrosesan data di Jupyter. Statistik pada n-gram dimuat dari JSON, post-processing dilakukan untuk dengan cepat menemukan kata yang dekat satu sama lain menurut Levenshtein, dan untuk pasangan dalam loop, fungsi (agak rumit) disebut yang mengatur kata-kata dan mengekstrak suntingan singkat dari bentuk ss → c (di bawah spoiler).


Perhitungan pengeditan itu sendiri terlihat sederhana, meskipun bisa memakan waktu lama.

Terapkan model kesalahan

Bagian ini diimplementasikan sebagai layanan mikro on Go, yang terhubung dengan backend utama melalui gRPC. Algoritma yang dijelaskan oleh Brill dan Moore sendiri [2], dengan sedikit optimasi, telah diimplementasikan. Sebagai hasilnya, itu berfungsi untuk saya, sekitar dua kali lebih lambat dari yang diklaim penulis; Saya tidak berani menilai apakah itu dalam Go atau di saya. Tetapi dalam proses pembuatan profil, saya belajar sedikit tentang Go.

• Jangan gunakan math.Max untuk menghitung maksimal. Ini sekitar tiga kali lebih lambat dibandingkan if a > b { b = a } ! Lihat saja implementasi dari fungsi ini :
  

   // Max returns the larger of x or y. // // Special cases are: // Max(x, +Inf) = Max(+Inf, x) = +Inf // Max(x, NaN) = Max(NaN, x) = NaN // Max(+0, ±0) = Max(±0, +0) = +0 // Max(-0, -0) = -0 func Max(x, y float64) float64 func max(x, y float64) float64 { // special cases switch { case IsInf(x, 1) || IsInf(y, 1): return Inf(1) case IsNaN(x) || IsNaN(y): return NaN() case x == 0 && x == y: if Signbit(x) { return y } return x } if x > y { return x } return y } 

  
  Kecuali jika Anda perlu +0 untuk menjadi lebih besar dari -0, jangan gunakan math.Max .
  
• Jangan gunakan tabel hash jika Anda bisa menggunakan array. Ini, tentu saja, saran yang sangat jelas. Saya harus memberi nomor baru karakter Unicode ke angka pada awal program untuk menggunakannya sebagai indeks dalam array turunan dari simpul trie (pencarian seperti itu adalah operasi yang sangat umum).
  
• Panggilan balik di Go tidak murah. Selama refactoring selama review kode, beberapa upaya saya untuk membuat decoupling secara signifikan memperlambat program meskipun fakta bahwa algoritma tidak berubah secara formal. Sejak itu, saya berpendapat bahwa kompilator pengoptimalan Go memiliki ruang untuk berkembang.
  

Terapkan model bahasa

Di sini, tanpa kejutan, algoritma pemrograman dinamis yang dijelaskan pada bagian di atas diimplementasikan. Komponen ini paling tidak berfungsi - bagian paling lambat adalah penerapan model kesalahan. Oleh karena itu, di antara dua lapisan ini, cache hasil model kesalahan di Redis juga kacau.

Hasil

Berdasarkan hasil pekerjaan ini (yang memakan waktu sekitar satu bulan), kami melakukan uji coba A / B pada pengguna kami. Alih-alih 10% dari hasil pencarian kosong di antara semua permintaan pencarian yang kami miliki sebelum pengenalan wali, ada 5% dari mereka; pada dasarnya, permintaan yang tersisa adalah untuk barang yang tidak kita miliki di platform. Jumlah sesi tanpa permintaan pencarian kedua juga telah meningkat (dan beberapa metrik lainnya yang terkait dengan UX). Namun, metrik yang terkait dengan uang tidak berubah secara signifikan - ini tidak terduga dan mengarahkan kami ke analisis menyeluruh dan pemeriksaan silang metrik lainnya.

Kesimpulan

Stephen Hawking pernah diberi tahu bahwa setiap formula yang dia masukkan dalam buku akan mengurangi separuh jumlah pembaca. Nah, dalam artikel ini ada sekitar lima puluh dari mereka - saya ucapkan selamat kepada Anda, salah satunya$$$10^{-10}$ Pembaca Mencapai Tempat Ini!

Bonus

Referensi

[1] MD Kernighan, Gereja KW, WA Gale. Program Koreksi Ejaan Berdasarkan Model Saluran Bising . Prosiding konferensi ke-13 tentang linguistik Komputasi - Volume 2, 1990.

[2] E.Brill, RC Moore. Model Kesalahan yang Ditingkatkan untuk Koreksi Ejaan Saluran Bising . Prosiding Pertemuan Tahunan ke-38 tentang Asosiasi untuk Linguistik Komputasi, 2000.

[3] T. Brants, AC Popat, P. Xu, FJ Och, J. Dean. Model Bahasa Besar dalam Terjemahan Mesin . Prosiding Konferensi 2007 tentang Metode Empiris dalam Pemrosesan Bahasa Alami.

[4] C. Daftar Putih, B. Hutchinson, GY Chung, G. Ellis. Menggunakan Web untuk Bahasa Pemeriksa Ejaan dan Autokoreksi Independen. Prosiding Konferensi 2009 tentang Metode Empiris dalam Pemrosesan Bahasa Alami: Volume 2.