🈷️ 🔨 🏪 Jaringan kerapatan campuran 🧑 ♣️ 🦈

Halo semuanya!

Mari kita bicarakan, seperti yang sudah Anda duga, jaringan saraf dan pembelajaran mesin. Dari namanya jelas apa yang akan diberitahukan tentang Mixture Density Networks, lalu hanya MDN, saya tidak ingin menerjemahkan nama dan membiarkannya apa adanya. Ya, ya, ya ... akan ada sedikit matematika yang membosankan dan teori probabilitas, tetapi tanpanya, sayangnya, atau untungnya, terserah Anda untuk memutuskan apakah sulit membayangkan dunia pembelajaran mesin. Tetapi saya segera meyakinkan Anda, itu akan relatif kecil dan tidak akan terlalu sulit. Bagaimanapun, Anda dapat melewatinya, tetapi lihat saja sejumlah kecil kode Python dan PyTorch, itu benar, kami akan menulis jaringan menggunakan PyTorch, serta berbagai grafik dengan hasilnya. Tetapi yang paling penting adalah bahwa akan ada kesempatan untuk memahami sedikit dan memahami apa itu jaringan MD.

Baiklah, mari kita mulai!

Regresi

Untuk memulainya, mari menyegarkan kembali sedikit pengetahuan kita dan mengingat, secara singkat, apa itu regresi linier .

Kami memiliki vektor

X = \ {x_1, x_2, ..., x_n \}

$X = \ {x_1, x_2, ..., x_n \}$ kita perlu memprediksi nilainya

$Y$ , yang entah bagaimana tergantung

$X$ menggunakan beberapa model linier:

$\ hat {Y} = X ^ T \ hat {\ beta}$

Sebagai fungsi kesalahan, kami akan menggunakan kesalahan kuadrat:

$SE (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 = \ sum_ {i = 1} ^ N (y_i-x_i ^ T \ hat {\ beta} ) ^ 2$

Masalah ini dapat diselesaikan secara langsung dengan mengambil turunan dari SE dan menetapkan nilainya ke nol:

$\ frac {\ delta SE (\ beta)} {\ delta \ beta} = 2X ^ T (\ mathbf {y} -X \ beta) = 0$

Dengan demikian, kami hanya menemukan minimumnya, dan SE adalah fungsi kuadrat, yang berarti bahwa minimum akan selalu ada. Setelah itu, Anda sudah bisa dengan mudah menemukannya

$\ beta$ :

$\ hat \ beta = (X ^ TX) ^ {- 1} X ^ T \ mathbf {y}$

Itu saja, masalahnya selesai. Di sinilah kita selesai mengingat apa itu regresi linier.

Tentu saja, ketergantungan yang melekat pada sifat pembuatan data dapat berbeda dan beberapa nonlinier harus sudah ditambahkan ke model kami. Memecahkan masalah regresi secara langsung untuk data besar dan nyata juga merupakan ide yang buruk, karena ada matriks

$X ^ TX$ dimensi

$n \ kali n$ , dan kita masih perlu menemukan matriks kebalikannya, dan sering terjadi bahwa matriks semacam itu tidak ada. Dalam hal ini, berbagai metode berdasarkan keturunan gradien datang ke bantuan kami. Non-linearitas model dapat diimplementasikan dengan berbagai cara, termasuk menggunakan jaringan saraf.

Tapi sekarang, mari kita bicara bukan tentang ini, tetapi tentang fungsi kesalahan. Apa perbedaan antara SE dan Log-Kemungkinan ketika data dapat memiliki hubungan non-linear?

Kami berurusan dengan kebun binatang, yaitu: OLS, LS, SE, MSE, RSS

Semua ini adalah satu dan sama pada intinya, RSS - jumlah sisa kuadrat, OLS - kuadrat terkecil biasa, LS - kuadrat terkecil, MSE - kuadrat galat, SE - kuadrat kesalahan. Di sumber yang berbeda Anda dapat menemukan nama yang berbeda. Inti dari ini hanya satu: deviasi kuadratik . Anda tentu saja bisa bingung, tetapi Anda terbiasa dengan cepat.

Perlu dicatat bahwa MSE adalah standar deviasi, nilai rata-rata tertentu dari kesalahan untuk seluruh rangkaian data pelatihan. Dalam praktiknya, MSE biasanya digunakan. Rumusnya tidak terlalu berbeda:

$MSE (\ beta) = \ frac {1} {N} \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2$

$N$ - ukuran dataset,

$\ hat {y} _i$ - prediksi model untuk

$y_i$ .

Hentikan itu! Kemungkinan? Ini adalah sesuatu dari teori probabilitas. Itu benar - itu teori probabilitas murni. Tetapi bagaimana deviasi kuadrat terkait dengan fungsi kemungkinan? Dan bagaimana hasilnya. Ini terhubung dengan menemukan kemungkinan maksimum (Kemungkinan maksimum) dan dengan distribusi normal, lebih tepatnya, dengan rata-rata

$\ mu$ .

Untuk menyadari bahwa ini benar, mari kita lihat kembali fungsi deviasi kuadrat:

$RSS (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 \ qquad \ qquad (1)$

Sekarang anggaplah bahwa fungsi kemungkinan memiliki bentuk normal, mis. Distribusi Gaussian atau normal:

$L (X) = p (X | \ theta) = \ prod ^ X \ mathcal {N} (x_i; \ mu, \ sigma ^ 2)$

Secara umum, apa fungsi kemungkinan dan apa artinya tidak akan saya sampaikan, Anda dapat membacanya di tempat lain, Anda juga harus membiasakan diri dengan konsep probabilitas bersyarat, teorema Bayes, dan banyak lagi, untuk pemahaman yang lebih dalam. Ini semua masuk ke teori probabilitas murni, yang dipelajari baik di sekolah maupun di universitas.

Sekarang, mengingat rumus distribusi normal, kita mendapatkan:

$L (X; \ mu, \ sigma ^ 2) = \ prod ^ X \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {(x_i- \ mu) ^ 2} {2 \ sigma ^ 2}} \ qquad \ qquad (2)$

Bagaimana jika kita menempatkan standar deviasi

$\ sigma ^ 2 = 1$ dan menghapus semua konstanta dalam rumus (2), cukup hapus, jangan kurangi, karena menemukan minimum fungsi tidak bergantung pada mereka. Maka kita akan melihat ini:

$L (X; \ mu, \ sigma ^ 2) \ sim \ prod ^ Xe ^ {- (x_i- \ mu) ^ 2}$

Masih belum ada yang suka? Tidak Nah, bagaimana jika kita mengambil logaritma dari fungsinya? Dari logaritma, ada beberapa keuntungan: multiplikasi akan berubah menjadi penjumlahan, derajat menjadi multiplikasi, dan

$\ log {e} = 1$ - untuk properti ini, perlu diperjelas bahwa kita berbicara tentang logaritma natural dan, sebenarnya

$\ ln {e} = 1$ . Dan secara umum, logaritma suatu fungsi tidak berubah secara maksimal, dan ini adalah fitur yang paling penting bagi kami. Hubungan dengan Log-Likelihood dan Likelihood dan mengapa ini akan berguna akan dijelaskan di bawah ini dalam penyimpangan kecil. Dan apa yang kami lakukan: menghapus semua konstanta, dan mengambil logaritma fungsi kemungkinan. Mereka juga menghilangkan tanda minus, sehingga mengubah Log-Likelihood menjadi Negative Log-Likelihood (NLL), koneksi di antara mereka juga akan digambarkan sebagai bonus. Hasilnya, kami mendapatkan fungsi NLL:

$\ log L (X; \ mu, I ^ 2) \ sim \ sum (X- \ mu) ^ 2$

Lihatlah fungsi RSS (1). Ya, mereka sama! Tepat! Juga terlihat itu

$\ mu = \ hat {y}$ .

Jika Anda menggunakan fungsi standar deviasi MSE, kami dapatkan dari ini:

$\ operatorname {argmin} MSE (\ beta) \ sim \ operatorname {argmax} \ mathbb {E} _ {X \ sim P_ {data}} \ log P_ {model} (x; \ beta)$

dimana

$\ mathbb {E}$ - Harapan matematika

$\ beta$ - parameter model, di masa depan kami akan menyatakannya sebagai:

$\ theta$ .

Kesimpulan: Jika kita menggunakan keluarga LS sebagai fungsi kesalahan dalam pertanyaan regresi, maka pada dasarnya kami memecahkan masalah menemukan fungsi kemungkinan maksimum dalam kasus ketika distribusi Gaussian. Dan nilai yang diprediksi

$\ hat {y}$ sama dengan rata-rata dalam distribusi normal. Dan sekarang kita tahu bagaimana semua ini terhubung, bagaimana teori probabilitas (dengan fungsi kemungkinannya dan distribusi normal) dan metode deviasi standar atau OLS saling terhubung. Rincian lebih lanjut tentang ini dapat ditemukan di [2].

Dan inilah bonus yang dijanjikan. Karena kita berbicara tentang hubungan antara berbagai fungsi kesalahan, kami akan mempertimbangkan (tidak harus dibaca):

Hubungan antara Entropi Silang, Kemungkinan, Log-Kemungkinan dan Negatif Log-Kemungkinan

Misalkan kita punya data

X = \ {x_1, x_2, x_3, x_4, ... \}

$X = \ {x_1, x_2, x_3, x_4, ... \}$ , setiap titik milik kelas tertentu, misalnya

\ {x_1 \ rightarrow1, x_2 \ rightarrow2, x_3 \ rightarrow n, ... \}

$\ {x_1 \ rightarrow1, x_2 \ rightarrow2, x_3 \ rightarrow n, ... \}$ . Total di sana

$n$ kelas, sedangkan kelas 1 terjadi

$c_1$ kali, kelas 2 -

$c_2$ waktu dan kelas

$n$ -

$c_n$ kali. Pada data ini kami melatih beberapa model

$\ theta$ . Fungsi kemungkinan (Kemungkinan) untuk itu akan terlihat seperti ini:

$P (1 | \ theta) P (2 | \ theta) ... P (n | \ theta) = \ prod ^ {c_1} \ hat {y} _1 \ prod ^ {c_2} \ hat {y} _2 ... \ prod ^ {c_n} \ hat {y} _n = \ hat {y} _1 ^ {c_1} \ hat {y} _2 ^ {c_2} ... \ hat {y} _n ^ {c_n}$

dimana

$P (n | \ theta) = \ hat {y} _n$ - probabilitas prediksi untuk kelas

$n$ .

Kami mengambil logaritma dari fungsi likelihood dan mendapatkan Log-Likelihood:

$\ log {P (data | \ theta)} = \ log {(\ hat {y} _1 ^ {c_1} ... \ hat {y} _n ^ {c_n})} = c_1 \ log {\ hat { y_1}} + ... + c_n \ log {\ hat {y_n}} = \ sum_i ^ n {c_i \ log {\ hat {y_i}}}$

Kemungkinan

$\ hat {y} \ dalam [0, 1]$ terletak pada kisaran 0 hingga 1, berdasarkan definisi probabilitas. Oleh karena itu, logaritma akan memiliki nilai negatif. Dan jika kita mengalikan Log-Likelihood dengan -1 kita mendapatkan fungsi Negatif Log-Likelihood (NLL):

$NLL = - \ log {P (data | \ theta)} = - \ sum_i ^ n {c_i \ log {\ hat {y_i}}}$

Jika kita membagi NLL dengan jumlah poin di

$X$ ,

$N = c_1 + c_2 + ... + c_n$ lalu kita dapatkan:

$- \ frac {1} {N} \ log {P (data | \ theta)} = - \ sum_i ^ n {\ frac {c_i} {N} \ log {\ hat {y_i}}} $$

dapat dicatat bahwa probabilitas nyata untuk kelas

$n$ sama dengan:

$y_n = \ frac {c_n} {N}$ . Dari sini kita dapatkan:

$NLL = - \ sum_i ^ n {y_i \ log {\ hat {y_i}}}$

sekarang jika Anda melihat definisi entropi silang

$H (p, q) = - \ jumlah {p \ log {q}}$ lalu kita dapatkan:

$NLL = H (y_i, \ hat {y_i})$

Dalam kasus ketika kita hanya memiliki dua kelas

$n = 2$ (klasifikasi biner) kami mendapatkan rumus untuk entropi silang biner (Anda juga dapat memenuhi nama Log-Loss):

$H (y, \ hat {y}) = - (y \ log {\ hat {y}} + (1-y) \ log {(1- \ hat {y})})$

Dari semua ini, dapat dipahami bahwa dalam beberapa kasus meminimalkan Cross-Entropy setara dengan meminimalkan NLL atau menemukan maksimum fungsi kemungkinan (Kemungkinan) atau Log-Likelihood.

Sebuah contoh Pertimbangkan klasifikasi biner. Kami memiliki nilai kelas:

y = np.array([0, 1, 1, 1, 1, 0, 1, 1]).astype(np.float32)

Peluang nyata

$y$ untuk kelas 0 sama

$2/8 = 0,25$ , untuk kelas 1 sama

$6/8 = 0,75$ . Misalkan kita memiliki classifier biner yang memprediksi probabilitas kelas 0

$\ hat {y}$ untuk setiap contoh, masing-masing, untuk kelas 1, probabilitasnya adalah

$(1- \ hat {y})$ . Mari kita plot nilai-nilai fungsi Log-Loss untuk prediksi yang berbeda

$\ hat {y}$ :

Pada grafik Anda dapat melihat bahwa minimum fungsi Log-Loss sesuai dengan poin 0.75, yaitu jika model kami benar-benar "mempelajari" distribusi data sumber,

$\ hat {y} = y$ .

Regresi Jaringan Saraf Tiruan

Jadi kami sampai pada praktik yang lebih menarik. Mari kita lihat bagaimana Anda bisa menyelesaikan masalah regresi menggunakan jaringan saraf (neural networks). Kami akan mengimplementasikan segala sesuatu dalam bahasa pemrograman Python, untuk membuat jaringan kami menggunakan pustaka pembelajaran mendalam PyTorch.

Sumber data generasi

Masukkan data

$\ mathbf {X} \ in \ mathbb {R} ^ N$ menghasilkan menggunakan distribusi seragam, ambil interval dari -15 ke 15,

$\ mathbf {X} \ dalam U [-15, 15]$ . Poin

$\ mathbf {Y}$ kita dapat menggunakan persamaan:

$\ mathbf {Y} = 0,5 \ mathbf {X} + 8 \ sin (0,3 \ mathbf {X}) + noise \ qquad \ qquad (3)$

dimana

$noise$ Merupakan vektor derau dimensi

$N$ diperoleh dengan menggunakan distribusi normal dengan parameter:

$\ mu = 0, \ sigma ^ 2 = 1$ .

Pembuatan data

 N = 3000 #   IN_DIM = 1 OUT_DIM = IN_DIM x = np.random.uniform(-15., 15., (IN_DIM, N)).T.astype(np.float32) noise = np.random.normal(size=(N, 1)).astype(np.float32) y = 0.5*x+ 8.*np.sin(0.3*x) + noise #  3 x_train, x_test, y_train, y_test = train_test_split(x, y) #

Grafik dari data yang diterima.

Membangun jaringan

Buat jaringan umpan maju biasa atau FFNN.

Membangun FFNN

 class Net(nn.Module): def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=40): super(Net, self).__init__() self.fc = nn.Linear(input_dim, layer_size) self.logit = nn.Linear(layer_size, out_dim) def forward(self, x): x = F.tanh(self.fc(x)) #  4 x = self.logit(x) return x

Jaringan kami terdiri dari satu lapisan tersembunyi dengan dimensi 40 neuron dan dengan fungsi aktivasi - garis singgung hiperbolik:

$\ tanh x = \ frac {e ^ x-e ^ {- x}} {e ^ x + e ^ {- x}} \ qquad \ qquad (4)$

Lapisan output adalah transformasi linear normal tanpa fungsi aktivasi.

Belajar dan mendapatkan hasil

Sebagai pengoptimal, kami akan menggunakan AdamOptimizer. Jumlah zaman studi = 2000, tingkat belajar (tingkat belajar atau lr) = 0,1.

Pelatihan FFNN

 def train(net, x_train, y_train, x_test, y_test, epoches=2000, lr=0.1): criterion = nn.MSELoss() optimizer = optim.Adam(net.parameters(), lr=lr) N_EPOCHES = epoches BS = 1500 n_batches = int(np.ceil(x_train.shape[0] / BS)) train_losses = [] test_losses = [] for i in range(N_EPOCHES): for bi in range(n_batches): x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS) x_train_var = Variable(torch.from_numpy(x_batch)) y_train_var = Variable(torch.from_numpy(y_batch)) optimizer.zero_grad() outputs = net(x_train_var) loss = criterion(outputs, y_train_var) loss.backward() optimizer.step() with torch.no_grad(): x_test_var = Variable(torch.from_numpy(x_test)) y_test_var = Variable(torch.from_numpy(y_test)) outputs = net(x_test_var) test_loss = criterion(outputs, y_test_var) test_losses.append(test_loss.item()) train_losses.append(loss.item()) if i%100 == 0: sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f' %(i, test_loss.item(), loss.item())) sys.stdout.flush() return train_losses, test_losses net = Net() train_losses, test_losses = train(net, x_train, y_train, x_test, y_test)

Sekarang mari kita lihat hasil pembelajaran.

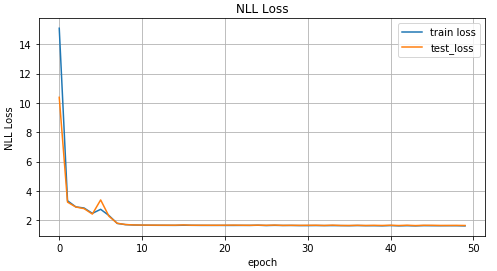
Grafik nilai fungsi UMK tergantung pada iterasi pelatihan, grafik nilai untuk data pelatihan dan data uji.

Hasil nyata dan prediksi pada data uji.

Data terbalik

Kami menyulitkan tugas dan membalikkan data.

Pembalikan data

 x_train_inv = y_train y_train_inv = x_train x_test_inv = y_train y_test_inv = x_train

Grafik Data Terbalik.

Untuk prediksi

$\ mathbf {\ hat Y}$ mari kita gunakan jaringan distribusi langsung dari bagian sebelumnya dan lihat bagaimana ia menangani ini.

 inv_train_losses, inv_test_losses = train(net, x_train_inv, y_train_inv, x_test_inv, y_test_inv)

Grafik nilai fungsi UMK tergantung pada iterasi pelatihan, grafik nilai untuk data pelatihan dan data uji.

Hasil nyata dan prediksi pada data uji.

Seperti yang dapat Anda lihat dari grafik di atas, jaringan kami sama sekali tidak mengatasi data seperti itu, hanya saja tidak dapat memprediksikannya. Dan semua ini terjadi karena dalam masalah terbalik untuk satu titik

$x$ dapat sesuai dengan beberapa poin

$y$ . Anda bertanya, bagaimana dengan kebisingan? Dia juga menciptakan situasi di mana untuk satu

$x$ bisa mendapatkan beberapa nilai

$y$ . Ya itu benar. Tetapi intinya adalah bahwa, meskipun kebisingan, itu semua adalah distribusi yang pasti. Dan karena model kami pada dasarnya diprediksi

$p (y | x)$ , dan dalam kasus MSE, itu adalah nilai rata-rata untuk distribusi normal (mengapa dijelaskan di bagian pertama artikel), kemudian diatasi dengan baik dengan tugas "langsung". Kalau tidak, kami mendapatkan beberapa distribusi yang berbeda untuk satu

$x$ dan karenanya kami tidak bisa mendapatkan hasil yang baik hanya dengan satu distribusi normal.

Jaringan kerapatan campuran

Kesenangan dimulai! Apa itu Jaringan Campuran Kepadatan (selanjutnya disebut jaringan MDN atau MD)? Secara umum, ini adalah model tertentu yang dapat mensimulasikan beberapa distribusi sekaligus:

$p (\ mathbf {y} | \ mathbf {x}; \ theta) = \ sum_k ^ K \ pi_k (\ mathbf {x}) \ mathcal {N} (\ mathbf {y}; \ mu_k (\ mathbf { x}), \ sigma ^ 2 (\ mathbf {x})) \ qquad \ qquad (5)$

Formula yang aneh, katamu. Mari kita cari tahu. Jaringan MD kami sedang belajar untuk memodelkan nilai tengah

$\ mu$ dan varians

$\ sigma ^ 2$ untuk beberapa distribusi. Dalam rumus (5)

$\ pi_k (\ mathbf {x})$ - yang disebut faktor signifikansi dari distribusi terpisah untuk setiap titik

$x_i \ in \ mathbf {x}$ , faktor pencampuran tertentu, atau berapa banyak masing-masing distribusi berkontribusi pada titik tertentu. Total di sana

$K$ distribusi.

Beberapa kata lagi tentang

$\ pi_k (\ mathbf {x})$ - pada kenyataannya, ini juga merupakan distribusi dan mewakili probabilitas untuk suatu titik

$x_i \ in \ mathbf {x}$ akan menjadi suatu kondisi

$k$ .

Fuh, sekali lagi, matematika ini, mari kita sudah menulis sesuatu. Maka, kita akan mulai mewujudkan jaringan. Untuk jaringan kami, kami ambil

$K = 30$ .

 self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance

Tentukan lapisan output untuk jaringan kami:

 x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x)

Kami menulis fungsi kesalahan atau fungsi kerugian, rumus (5):

 def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses))

Kode Bangun MDN Lengkap

 COEFS = 30 class MDN(nn.Module): def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=50, coefs=COEFS): super(MDN, self).__init__() self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance self.out_dim = out_dim self.coefs = coefs def forward(self, x): x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x) return pi, mu, sigma_sq #       def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) #   def loss_fn(y, pi, mu, sigma_sq): losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses)) return loss

Jaringan MD kami siap untuk digunakan. Hampir siap. Tetap melatihnya dan melihat hasilnya.

Pelatihan MDN

 def train_mdn(net, x_train, y_train, x_test, y_test, epoches=1000): optimizer = optim.Adam(net.parameters(), lr=0.01) N_EPOCHES = epoches BS = 1500 n_batches = int(np.ceil(x_train.shape[0] / BS)) train_losses = [] test_losses = [] for i in range(N_EPOCHES): for bi in range(n_batches): x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS) x_train_var = Variable(torch.from_numpy(x_batch)) y_train_var = Variable(torch.from_numpy(y_batch)) optimizer.zero_grad() pi, mu, sigma_sq = net(x_train_var) loss = loss_fn(y_train_var, pi, mu, sigma_sq) loss.backward() optimizer.step() with torch.no_grad(): if i%10 == 0: x_test_var = Variable(torch.from_numpy(x_test)) y_test_var = Variable(torch.from_numpy(y_test)) pi, mu, sigma_sq = net(x_test_var) test_loss = loss_fn(y_test_var, pi, mu, sigma_sq) train_losses.append(loss.item()) test_losses.append(test_loss.item()) sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f' %(i, test_loss.item(), loss.item())) sys.stdout.flush() return train_losses, test_losses mdn_net = MDN() mdn_train_losses, mdn_test_losses = train_mdn(mdn_net, x_train_inv, y_train_inv, x_test_inv, y_test_inv)

Grafik nilai fungsi kerugian tergantung pada iterasi pelatihan, grafik nilai untuk data pelatihan dan data uji.

Karena jaringan kami telah mempelajari nilai rata-rata untuk beberapa distribusi, mari kita lihat ini:

 pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv)))

Grafik untuk dua nilai rata-rata yang paling mungkin untuk setiap titik (kiri). Grafik untuk 4 nilai rata-rata yang paling mungkin untuk setiap titik (kanan).

Grafik untuk semua nilai rata-rata untuk setiap titik.

Untuk memprediksi data, kami akan secara acak memilih beberapa nilai

$\ mu$ dan

$\ sigma ^ 2$ berdasarkan nilai

$\ pi_k (\ mathbf {x})$ . Dan kemudian berdasarkan pada mereka untuk menghasilkan data target

$\ hat {y}$ menggunakan distribusi normal.

Prediksi Hasil

 def rand_n_sample_cumulative(pi, mu, sigmasq, samples=10): n = pi.shape[0] out = Variable(torch.zeros(n, samples, OUT_DIM)) for i in range(n): for j in range(samples): u = np.random.uniform() prob_sum = 0 for k in range(COEFS): prob_sum += pi.data[i, k] if u < prob_sum: for od in range(OUT_DIM): sample = np.random.normal(mu.data[i, k*OUT_DIM+od], np.sqrt(sigmasq.data[i, k])) out[i, j, od] = sample break return out pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv))) preds = rand_n_sample_cumulative(pi, mu, sigma_sq, samples=10)

Data yang diprediksi untuk 10 nilai yang dipilih secara acak

$\ mu$ dan

$\ sigma ^ 2$ (kiri) dan dua (kanan).

Dapat dilihat dari angka-angka bahwa MDN melakukan pekerjaan yang sangat baik dengan tugas "terbalik".

Menggunakan data yang lebih kompleks

Mari kita lihat bagaimana jaringan MD kami menangani data yang lebih kompleks, seperti data spiral. Persamaan spiral hiperbolik dalam koordinat Cartesian:

$x = \ rho \ cos \ phi \\ qquad \ qquad \ qquad \ qquad \ qquad \ qquad (6) \\ y = \ rho \ sin \ phi \\$

Pembuatan Data Spiral

 N = 2000 x_train_compl = [] y_train_compl = [] x_test_compl = [] y_test_compl = [] noise_train = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32) noise_test = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32) for i, theta in enumerate(np.linspace(0, 5*np.pi, N).astype(np.float32)): #  6 r = ((theta)) x_train_compl.append(r*np.cos(theta) + noise_train[i]) y_train_compl.append(r*np.sin(theta)) x_test_compl.append(r*np.cos(theta) + noise_test[i]) y_test_compl.append(r*np.sin(theta)) x_train_compl = np.array(x_train_compl).reshape((-1, 1)) y_train_compl = np.array(y_train_compl).reshape((-1, 1)) x_test_compl = np.array(x_test_compl).reshape((-1, 1)) y_test_compl = np.array(y_test_compl).reshape((-1, 1))

Grafik data spiral.

Untuk bersenang-senang, mari kita lihat bagaimana jaringan Feed-Forward reguler akan mengatasi tugas seperti itu.

Seperti yang diharapkan, jaringan Feed-Forward tidak dapat menyelesaikan masalah regresi untuk data tersebut.

Kami menggunakan jaringan MD yang dijelaskan dan dibuat sebelumnya untuk pelatihan data spiral.

Jaringan Campuran Kepadatan melakukan pekerjaan yang baik dalam situasi ini.

Kesimpulan

Pada awal artikel ini, kami mengingat dasar-dasar regresi linier. Kami melihat bahwa secara umum antara menemukan rata-rata untuk distribusi normal dan MSE. Dibongkar bagaimana terhubung NLL dan cross entropy. Dan yang paling penting, kami menemukan model MDN, yang dapat belajar dari data yang diperoleh dari distribusi campuran. Saya harap artikel ini bisa dimengerti dan menarik, meskipun ada sedikit matematika.

Kode lengkap dapat dilihat di GitHub .

Sastra

Jaringan Campuran Kepadatan (Christopher M. Bishop, Neural Computing Research Group, Departemen Ilmu Komputer dan Matematika Terapan, Universitas Aston, Birmingham) - artikel yang sepenuhnya menjelaskan teori jaringan MD.
Kuadrat terkecil dan kemungkinan maksimum (MROsborne)

Jaringan kerapatan campuran

Regresi

Regresi Jaringan Saraf Tiruan

Sumber data generasi

Membangun jaringan

Belajar dan mendapatkan hasil

Data terbalik

Jaringan kerapatan campuran

Menggunakan data yang lebih kompleks

Kesimpulan

Sastra

More articles: