Halo
Dalam artikel saya sebelumnya, saya berbicara tentang bagaimana saya membuat
animasi planet-planet tata surya untuk anak saya. Terima kasih untuk semua orang atas umpan balik dan sambutan hangat. Hari ini saya telah menyiapkan beberapa animasi yang lebih menarik, yang dipersatukan secara kondisional dengan tema “gerak melingkar dan osilasi”. Dengan kata lain, apa yang digambarkan oleh cosinus dan sinus.

Untuk rendering, saya menggunakan javascript dan kanvas. Untuk setiap contoh, tautan diberikan di mana Anda dapat dengan cermat melihat semuanya. Anda dapat melihat ke dalam kode sumber, Anda dapat menyalin sendiri - Saya tidak keberatan. Materi mungkin berguna dalam kelas dan pilihan dalam fisika, matematika atau ilmu komputer.
Jadi ayo pergi.
Lintasan bulan
Mari kita mulai dengan mekanika selestial. Pertanyaan favorit saya untuk anak sekolah: “Bumi bergerak [hampir] dalam lingkaran di sekitar Matahari, dan Bulan - dalam lingkaran di sekitar Bumi. Seperti apa lintasan bulan dalam kerangka referensi matahari? " Saya harap para pembaca yang budiman akan lebih siap dan tidak akan mulai menggambar "ikal" seperti itu:
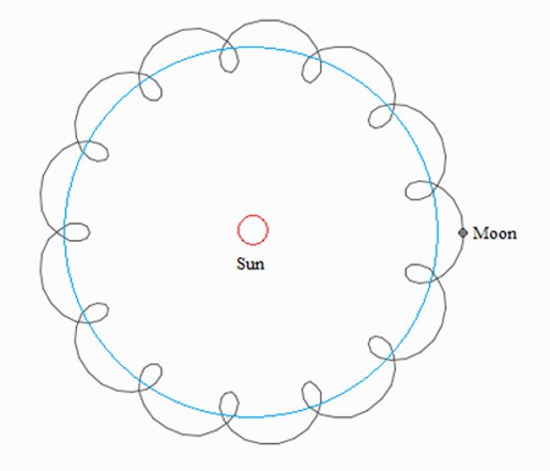
Meskipun lintasan seperti itu cocok dengan akal sehat, itu tidak terjadi secara khusus dengan Bulan. Faktanya, Bumi "bergegas" di orbit, dan Bulan, sebagaimana terlampir, entah sedikit ke kiri atau sedikit ke kanan. Memang: kecepatan orbital Bumi adalah ~ 30 km / s, dari Bulan - sekitar 1 km / s. Jelas, kecepatan bulan tidak cukup untuk bergerak ke arah yang berlawanan. Penjelasan yang lebih akurat dikaitkan dengan perhitungan gaya yang bekerja di Bulan (dari sisi Bumi dan Matahari) dan di mana jari-jari lengkungan lintasan diarahkan (saya akan meninggalkan ini untuk studi independen).
Jadi, secara teori, tampaknya jelas. Tapi masih ada beberapa pernyataan. Saya ingin melihat bagaimana sebenarnya. Mari kita membuat
model pada skala 1 pixel = 30.000 km. Ini adalah opsi kompromi sehingga orbitnya dapat dibedakan, meskipun skala gambarnya masih sangat besar: 15000 * 15000 piksel. Dalam animasi, gerakan Bumi dan Bulan dijelaskan oleh hukum gerak melingkar: lintasan biru untuk Bumi, dan hitam untuk Bulan. Setelah menggambar, Anda bisa melihat hasilnya. Orang dapat melihat seberapa kecil total penyimpangan orbit Bulan dari orbit Bumi. Berikut adalah contoh potongan kecil gambar:

Agar gambar-gambar di internet sangat terdistorsi, Anda perlu mengingat ini.
By the way, demi kepentingan, Anda dapat membuat animasi yang sama dengan beberapa satelit Jupiter. Secara teori, seharusnya sudah ada "ikal."
Angka-angka lissajous
Sekali waktu, ketika saya belajar di sekolah fisika dan fisika Novosibirsk, kami memiliki pekerjaan laboratorium "Angka Lissajous", sebagaimana mestinya, dengan generator dan osiloskop Soviet. Itu terlihat menyeluruh dan menarik. Bergantung pada frekuensi sinyal yang dipasok ke input, berbagai bentuk diperoleh pada layar osiloskop:
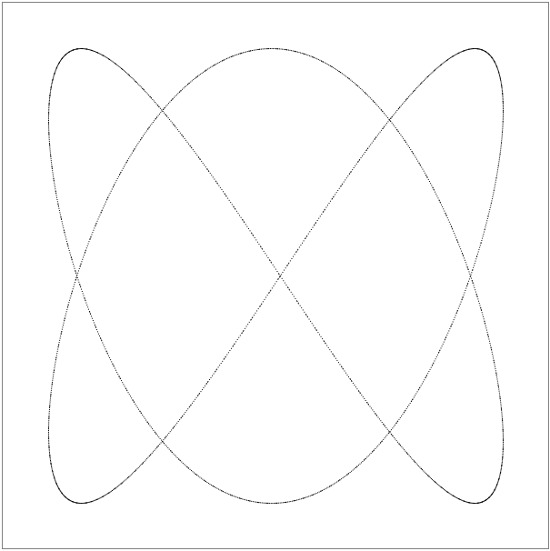
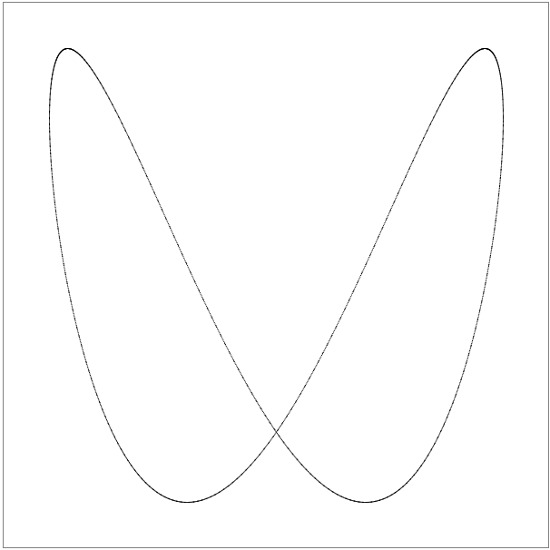
Faktanya, setiap gambar adalah tambahan dari dua getaran simultan - sepanjang sumbu X dan sepanjang sumbu Y. Frekuensi getaran ini dapat dikorelasikan sebagai 1: 1 (satu osilasi sepanjang X, satu sepanjang Y; satu lingkaran, elips atau garis lurus dapat diperoleh), 1: 2 (satu dalam X, dua dalam Y; parabola atau "pelana" diperoleh), 1: 3, 2: 3 (angka yang lebih kompleks) dan seterusnya - saya pikir Anda memahami prinsipnya. Anda dapat menemukan dasar teoretis terperinci di
Wikipedia , dan saya menyiapkan
halaman terpisah di mana Anda dapat "bermain-main" dengan berbagai koefisien.
Parameter yang menarik adalah pergeseran fase antara osilasi. Jika terus berubah, maka sosok "hidup kembali" - mulai berputar. Di sini, pertanyaan favorit saya adalah: "dan ke arah mana ia berputar?" Seseorang mengatakan bahwa dalam satu arah, seseorang - bahwa di arah lain, tetapi secara umum Anda dapat "mengalihkan" arah rotasi saat bepergian. Ini murni masalah persepsi. Cobalah dan lakukanlah.
Kami menyulitkan animasi kami dengan menambahkan
atenuasi . Dalam hal ini, titik secara bertahap “jatuh” ke tengah, tetapi, sekali lagi, di sepanjang lintasan yang rumit dan agak indah.

Ngomong-ngomong, ini bisa dilakukan langsung. Seperti yang disarankan dalam satu buku, Anda perlu membuat silinder dengan lubang kecil di bagian bawah, tuangkan semolina di sana, gantung di ambang pintu dan ayunkan. Semolina yang kosong hanya akan menggambar sosok Lissajous yang pudar.
Spirograph
Sebuah mainan dari kenangan masa kecil, ketika saya, pada usia 6-7 tahun, melukis pola mengunjungi nenek saya:

Jika tiba-tiba seseorang, karena kebetulan yang tidak pernah terdengar, tidak terbiasa dengan keajaiban ini, kemudian lari ke
Wikipedia . Kami akan melihat halaman
animasi . Hanya ada tiga parameter, seperti dalam spirograph nyata: jari-jari lingkaran kecil / besar dan jarak dari titik ke pusat lingkaran kecil. Tetapi kombinasi mereka yang berbeda memberikan sejumlah besar pola (contoh yang Anda lihat di awal artikel ini).
Ngomong-ngomong, satu fitur menarik ditemukan di dalam skrip: di dalamnya Anda dapat mengatur kombinasi yang tidak mungkin dilakukan dalam spirograph nyata - misalnya, membuat
lingkaran bagian dalam lebih besar daripada bagian luar , atau bahkan
membuat lubang di luar lingkaran bagian dalam . Program ini memungkinkan Anda untuk menghasilkan apa pun yang Anda inginkan.
Hasil
Mari kita simpulkan. Seperti yang Anda lihat, animasi kami ada di persimpangan fisika dan ilmu komputer. Sangat bagus dan menarik untuk membaca tentang bulan atau tokoh-tokoh Lissajous yang sama, tetapi sangat bagus dan menarik untuk melihatnya di layar dan “bermain-main” dengan parameter. Tentu saja, jika ada benda nyata untuk mendapatkan hasilnya, maka, tentu saja, Anda harus menggunakannya (misalnya, perangkat elektronik - generator, osiloskop - untuk mengamati angka-angka Lissajous). Saya umumnya adalah pendukung "bekerja dengan tangan." Tetapi seringkali tidak ada yang cocok - dalam kasus seperti itu, animasi pada komputer membantu.
Saya juga ingin secara terpisah mencatat komponen estetika. Alam, dalam keyakinan pribadi saya, sangat indah pada intinya. Setuju, senang melihat formula pendek dan sederhana yang menggambarkan seluruh kelas fenomena. Atau, sekali lagi, ke representasi grafis dari beberapa rumus (seperti dengan spirograph). Dan, misalnya, garis medan magnet? Dan hasil dari tabrakan partikel? Saya ingat bahwa di universitas kami juga membuat solusi persamaan diferensial - bahkan ada keanggunan dan keindahan. Jika Anda tahu semua ini dan mengerti apa yang saya bicarakan - mari kita berjabat tangan satu sama lain. Dan jika Anda sekarang tertarik pada ini, untuk Anda semuanya baru saja dimulai. Hari ini adalah langkah pertama.