Genetika kultivar Romanesco: model matematika fraktal ekspresi gen

Apa kesamaan kepingan salju, kubis Romanesco, bintang laut, kilat, dan pohon? Anda tidak akan langsung mengatakannya, tetapi dari sudut pandang matematika, semua objek ini memiliki fitur umum - fraktalitas. Di mata matematika, segala sesuatu di dunia kita mematuhi hukum "Ratu Ilmu Pengetahuan". Fenomena, proses, atau objek apa pun dapat diekspresikan dalam bentuk matematika, yang memungkinkannya dianalisis dari sudut pandang yang baru, begitulah. Selama bertahun-tahun, para ilmuwan telah mencoba menciptakan representasi matematis gen yang sempurna, hubungan mereka dan proses di mana mereka terlibat. Hari ini kita akan berbicara tentang bagaimana fraktal membantu meletakkan dasar bagi model matematika gen manusia yang sepenuhnya baru dari perspektif kanker. Apa itu fraktal, mengapa begitu penting bagi ahli genetika dan matematikawan, dan bagaimana model matematika baru dapat membantu kedokteran modern? Kami akan mencari jawaban dalam laporan kelompok penelitian. Ayo pergi.

Retret teoretis

Untuk memulainya, ada baiknya mencari tahu apa itu fraktal dan dimakan dengan apa.

Fraktal adalah himpunan dengan sifat kesamaan diri. Sederhananya, ketika sesuatu terdiri dari beberapa salinan mini itu sendiri.



Fraktal ditemukan dalam berbagai fenomena fisik: dari difusi hingga turbulensi. Ini bisa disebut manifestasi alami fraktal. Orang-orang juga menemukan penggunaan fraktal: dalam grafik komputer, teknik radio, teknologi jaringan, dll.

Fraktal sangat berwarna dalam film "Doctor Strange" (2016), ketika Tetua mengirim protagonis dalam perjalanan sepanjang dimensi paralel.


Pemandangan yang agak tidak menyenangkan, tetapi jelas menunjukkan fraktur.

Bahkan di rak-rak supermarket Anda dapat menemukan manifestasi fraktur, yaitu, contoh kubis atau kembang kol Romanesco.

Jika kita memperhitungkan bahwa ada cukup banyak jenis set dengan properti fraktal, dapat dikatakan bahwa hampir semua yang ada di sekitar kita dalam satu atau lain cara terhubung dengan fraktal. Dan tubuh manusia, terutama gennya, tidak terkecuali. Karena fraktal dapat dijelaskan secara matematis dengan mengurutkan komponen, penggunaan model seperti itu pada gen manusia dapat secara signifikan membantu dalam memahami berbagai proses yang terjadi dalam tubuh kita, termasuk berbagai penyakit, patologi, dan hal-hal tidak menyenangkan lainnya.

Salah satu proses terpenting dalam tubuh kita adalah ekspresi gen (gambar 1a ), ketika informasi herediter gen diubah menjadi produk fungsional. Dengan kata lain, sel-sel kita melalui ekspresi gen mengontrol struktur dan fungsinya. Gen kita adalah basis data dari mana semua sel tubuh memperoleh informasi, melakukan fungsi yang diperlukan setelahnya. Karena itu, mulut kita tidak menumbuhkan rambut, sistem kekebalan tubuh melawan infeksi, pengangkutan sel darah, dll. Semua proses ini terjadi tepat karena pemrograman sel untuk melakukan tugas tertentu, yang pada gilirannya dimungkinkan melalui sintesis protein dari aktivasi gen tertentu.


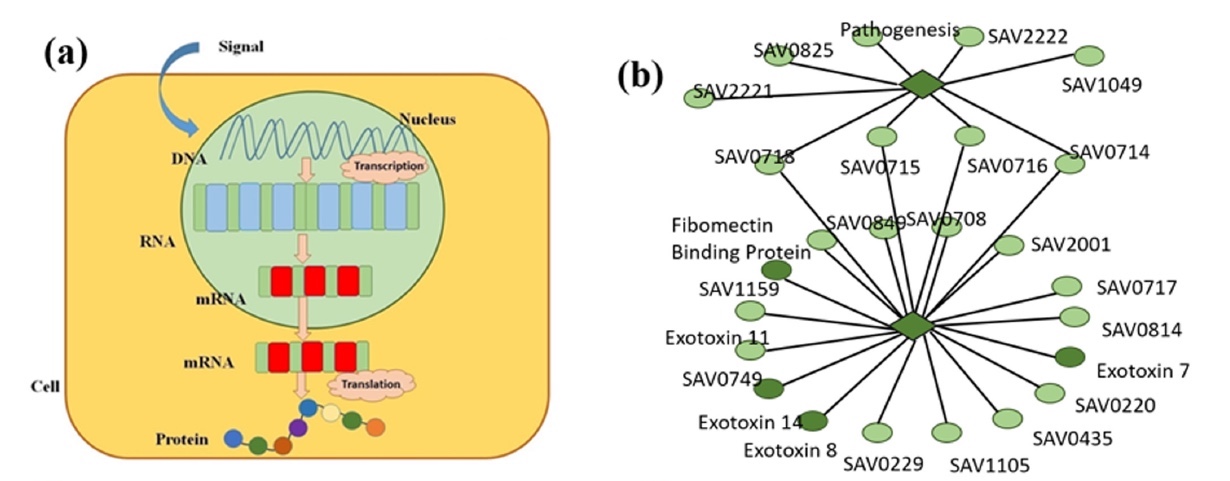Gambar No. 1

Regulasi ekspresi gen menunjukkan kapan, berapa banyak, dan berapa lama protein tertentu harus diproduksi. Oleh karena itu, studi tentang proses ini sangat penting untuk pemahaman penuh tentang bagaimana mekanisme pengendalian organisme tertentu bekerja.

Proses kompleks ini penting bagi para ilmuwan, karena memiliki kesempatan untuk mengendalikannya, mereka akan dapat membuat sel sintetis tertentu yang diberkahi dengan fungsi yang jelas, khususnya, pengiriman obat kanker ke "jantung" penyakit untuk pengobatan yang lebih efektif.

Untuk meningkatkan metode pengobatan penyakit seperti itu, perlu untuk mempelajari aspek genetik secara lebih rinci. Untuk melakukan ini, para ilmuwan mengusulkan untuk menyajikan tubuh manusia dalam bentuk program, di mana gen bertindak sebagai garis kode yang dapat diubah jika program bekerja dengan kegagalan. Untuk mewujudkan ini, Anda harus terlebih dahulu membuat model matematika gen. Saat ini, model seperti itu sudah ada, tetapi mereka tidak dapat mewakili karena mereka bertujuan mempelajari dinamika dalam jaringan gen. Dalam studi yang sama ini, yang menerapkan konsep fraktal, para ilmuwan memutuskan untuk fokus pada proses ekspresi gen tertentu, dan kemudian menerapkan korelasi silang antara pasangan gen- FT * ( 1b ).

Transcription factor (FT) * adalah protein kontrol sintesis mRNA yang berisi informasi tentang struktur primer protein pada matriks DNA dengan menghubungkan ke situs DNA tertentu.

Sederhananya, para ilmuwan memutuskan untuk menggali lebih dalam, setelah memeriksa bukan seluruh "dinding" secara keseluruhan, tetapi "batu bata" individu.

Hasil penelitian

Subjek uji dalam penelitian ini adalah jamur Saccharomyces cerevisiae (ragi roti) dan bakteri Escherichia coli (Escherichia coli).

Dengan menganalisis data statistik dari ekspresi genetik subjek percobaan, koefisien Hurst * dihitung.

Koefisien Hurst * adalah ukuran analisis deret waktu.

Rangkaian waktu * - satu set data statistik yang dikumpulkan pada interval waktu yang berbeda tentang suatu indikator.

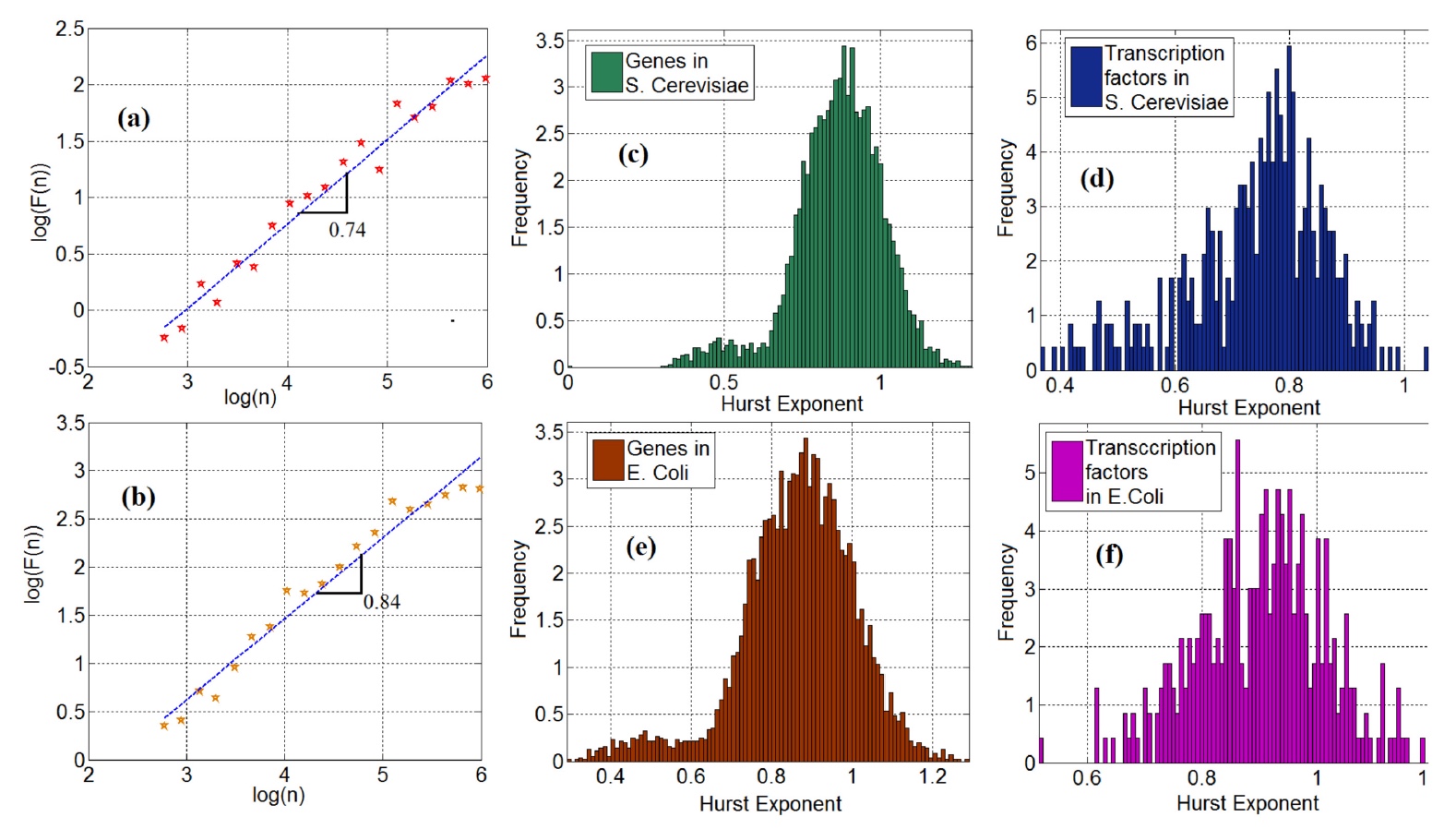Gambar No. 2

Gambar 2a (ragi) dan 2b (Escherichia coli) menunjukkan grafik bilogaritmik * fluktuasi sebagai fungsi dari skala deret waktu FT.

Grafik Bilogaritmik * adalah grafik data dua dimensi menggunakan skala logaritmik pada kedua sumbu (vertikal dan horizontal).

Kemiringan kurva dalam grafik ini sesuai dengan koefisien Hurst. Perlu dicatat bahwa 95% (ragi) dan 98% (bacillus) dari seri waktu gen menunjukkan ketergantungan jangka panjang * .

Ketergantungan jangka panjang * - sebuah indikator dalam analisis deret waktu, yang menunjukkan pelemahan lambat dari ketergantungan statistik dua titik dengan peningkatan interval waktu di antara mereka. Ini ditentukan oleh indikator koefisien Hurst - dari 0 hingga 1. Jika indikator di atas 0,5, maka kita memiliki hubungan jangka panjang yang kuat, di bawah 0,5 - efek sebaliknya.

Koefisien Hurst dari ketergantungan jangka panjang dalam kasus khusus ini adalah 0,5, yang menunjukkan ketidakhadirannya, secara teori. Namun, analisis lebih lanjut dari data menunjukkan bahwa indikator ini melebihi nilai 0,5, yang menunjukkan adanya ketergantungan jangka panjang dari deret waktu dalam ekspresi genetik ( 2c dan 2e ). Ini menunjukkan bahwa deret waktu gen-FT tidak dapat dianggap sebagai sesuatu yang acak, oleh karena itu mereka harus dimodelkan berdasarkan rantai Markov ketika ada serangkaian peristiwa, keacakan masing-masing yang hanya bergantung pada peristiwa sebelumnya.

Seperti halnya gen, faktor transkripsi juga menunjukkan hubungan jangka panjang: pada 97% untuk ragi dan untuk basil (grafik 2d dan 2f ).

Sekarang tambahkan sedikit analisis fraktal ke mangkuk umum. Untuk memulainya, para ilmuwan menarik perhatian kita pada bimodalitas distribusi koefisien Hurst. Ini paling baik dilihat pada grafik 2c dan 2e. Para ilmuwan menjelaskan pengamatan ini dengan fakta bahwa ada proses difusi dalam ekspresi gen yang memiliki beberapa potensi difusi. Oleh karena itu, bimodality dapat dijelaskan oleh gerakan Brownian yang tidak tenang dengan berbagai potensi. Namun pernyataan ini membutuhkan bukti tambahan, yang akan dicari para ilmuwan dalam studi berikut.

Dan sekarang kita akan kembali ke multifractality. Para ilmuwan menggunakan analisis multifractal dari fluktuasi detrend untuk menentukan ada / tidaknya karakteristik multifractal dalam rangkaian waktu ekspresi gen. Analisis ini menunjukkan adanya gen dan FT.

Para ilmuwan juga menerapkan metodologi bootstrap * untuk secara akurat menentukan (lebih tepatnya, untuk mengonfirmasi) keberadaan ketergantungan jangka panjang, mengingat panjang seri waktu eksperimental yang terbatas.

Bootstrap * - teknik untuk menganalisis statistik distribusi probabilitas.

Untuk setiap seri waktu ekspresi gen, 10 sub-interval acak disiapkan, masing-masing berisi 90% dari fragmen yang terurut dari seri waktu awal. Selanjutnya, untuk semua opsi, koefisien Hurst dihitung. Dengan demikian, perbedaan diperoleh antara indikator deret waktu eksperimental dan versi acak. Untuk E. coli, perbedaannya hanya 0,006%, dan untuk ragi roti bahkan kurang - 0,0001%. Dengan demikian, keberadaan ketergantungan jangka panjang pada kedua sampel dikonfirmasi.

Setelah mempertimbangkan karakteristik gen dan FT secara terpisah yang menarik, para ilmuwan mengatur tentang menganalisis pasangan gen-FT sebagai objek tunggal. Perhitungan indeks korelasi silang menunjukkan bahwa 98% pasangan gen-FT (pada kedua sampel) memiliki sifat ketergantungan jangka panjang ( 3a ).


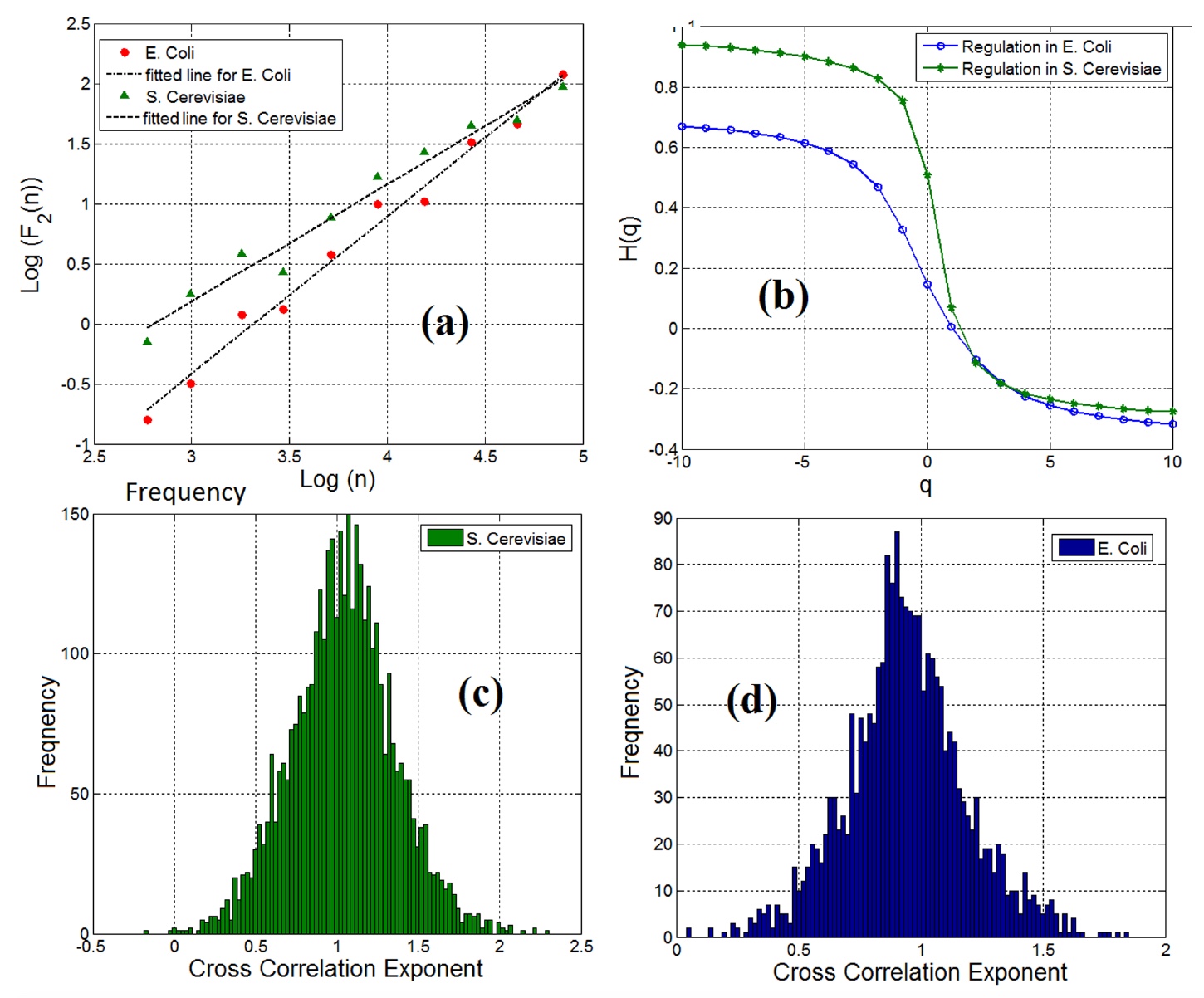Gambar No. 3

Analisis multifraktal terhadap fluktuasi detrend mengkonfirmasi adanya fitur multifraktal pada pasangan gen-FT (grafik 3b ).

Perlu dicatat bahwa terlepas dari fakta bahwa baik korelasi silang fraktal dan jangka panjang diamati pada pasangan gen dan faktor transkripsi dalam jaringan regulasi gen, korelasi silang tidak sama untuk semua pasangan. Grafik 3c (ragi) dan 3d (Escherichia coli) menunjukkan korelasi silang dari pasangan gen-FT.

Para ilmuwan menggunakan grafik ini untuk mengukur entropi informasi dan, sebagai hasilnya, konten informasi dari jaringan regulasi gen untuk berbagai jenis sel untuk analisis kuantitatif dan spesifikasi jaringan regulasi gen.Indikator entropi adalah: 4,18 - ragi, 5,29 - E. coli. Dan ini menunjukkan bahwa jaringan ekspresi gen dalam ragi roti jauh lebih besar dan menunjukkan dinamika yang lebih kompleks daripada jaringan ekspresi gen di Escherichia coli.

Dan sekarang hal yang paling menarik adalah penciptaan model matematika. Para ilmuwan telah memilih dua versi model: himpunan Mandelbrot dan himpunan dalam bentuk pohon diad wavelet.

Dengan menggunakan indikator koefisien Hölder yang diperoleh sebelumnya dalam spektrum multifraktal, para ilmuwan menemukan bahwa hanya 0,04 dari semua pasangan gen-FT dalam jaringan regulasi gen ragi roti dapat dimodelkan menggunakan set Mandelbrot. Dan pada E. coli, tidak satu pasangan pun dapat dimodelkan dengan metode ini.

Jika kita mempertimbangkan pasangan yang mampu mensimulasikan, maka ada perbedaan besar dalam data antara model dan pengamatan eksperimental. Sebagai kesimpulan, metode pemodelan karena set Mandelbrot tidak cocok.


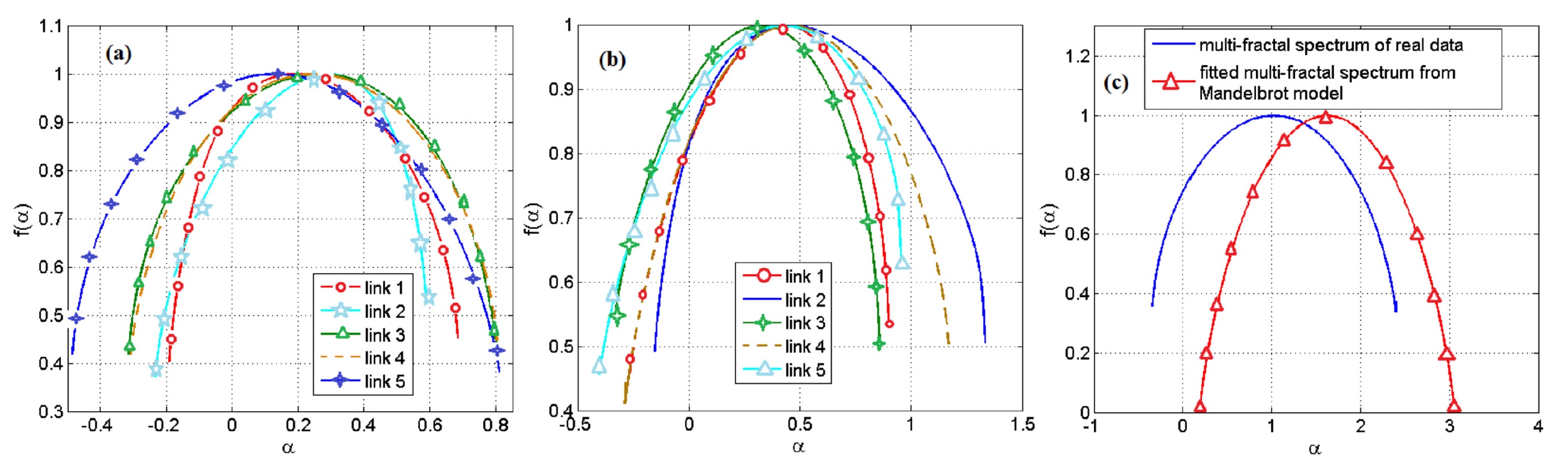Gambar No. 4

Hasil menggunakan model berdasarkan pada set Mandelbrot ditunjukkan pada grafik di atas. Yang paling terang adalah 4c , di mana kita bisa melihat seberapa banyak data berbeda.

Para ilmuwan juga membandingkan multifraktalitas yang diamati dari saling ketergantungan dalam jaringan regulasi gen dan model multifraktal kaskade acak pada pohon wavelet-diadik.

Para peneliti memutuskan untuk memeriksa apakah model logaritmik dari kaskade-W cocok untuk representasi pasangan gen-FT dalam jaringan regulasi gen. Berdasarkan spektrum empiris dan spektrum singularitas, parameter model ini dihitung. Selanjutnya, perhitungan dibuat dari bidang-bidang persimpangan dari spektra multifraktal yang dihitung dan empiris, rasio yang menjadi kriteria utama untuk menerima atau menolak model multifraktal matematika ini.


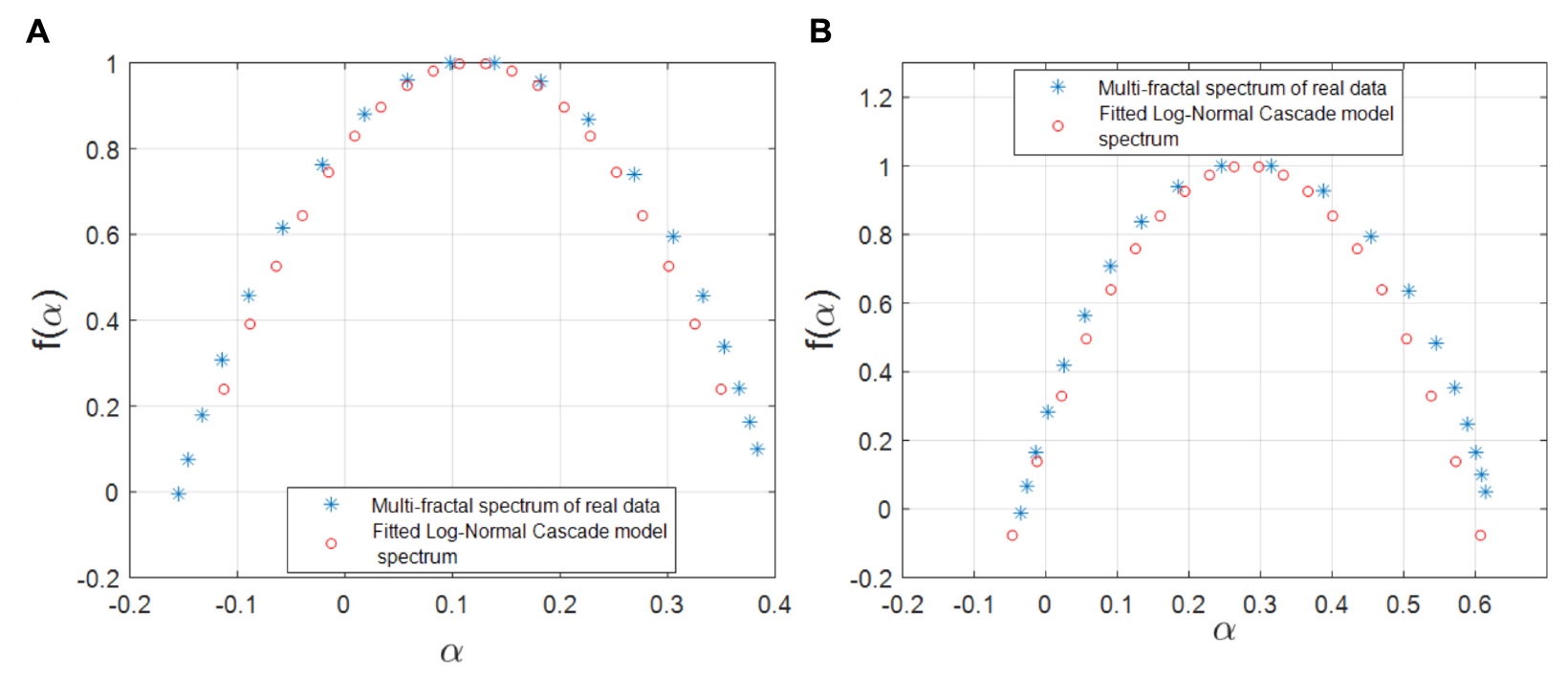Gambar No. 5

Seperti dapat dilihat dari grafik di atas, menunjukkan spektra multifraktal yang disimulasikan dan empiris, model ini hampir sepenuhnya berkorelasi dengan data pengamatan dan perhitungan yang dilakukan sebelumnya.

Untuk seorang kenalan yang lebih mendetail dengan nuansa penelitian, saya sarankan Anda melihat laporan kelompok riset di tautan ini .

Epilog

Studi ini, sebagian besar teoretis, memiliki potensi besar untuk penggunaan praktis, karena membantu secara matematis memodelkan jaringan untuk mengatur ekspresi gen - salah satu proses terpenting dalam organisme hidup. Proses kompleks sulit untuk dipahami, tidak peduli betapa anehnya kedengarannya. Untuk memudahkan tugas, perlu untuk membagi proses menjadi komponen, menyusun "peta" mereka, dan mengikuti rute yang diinginkan, mencatat semua fitur dan karakteristik penting. Pemodelan matematika, tidak seperti yang lain, sangat bagus untuk ini. Setelah mempelajari model matematika dari suatu objek atau proses, kita dapat memahami apa yang kita hadapi sebelum melanjutkan dengan mempelajari objek atau proses yang sebenarnya.

Studi ini sekali lagi menegaskan bahwa tidak hanya fisika dan kimia menguasai dunia, tetapi matematika jauh dari tempat terakhir di Olympus sains.

Terima kasih atas perhatian Anda, tetap ingin tahu dan selamat bekerja, kawan.

Terima kasih telah tinggal bersama kami. Apakah Anda suka artikel kami? Ingin melihat materi yang lebih menarik? Dukung kami dengan melakukan pemesanan atau merekomendasikannya kepada teman-teman Anda, diskon 30% untuk pengguna Habr pada analog unik dari server entry-level yang kami temukan untuk Anda: Seluruh kebenaran tentang VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps dari $ 20 atau bagaimana membagi server? (opsi tersedia dengan RAID1 dan RAID10, hingga 24 core dan hingga 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps hingga 1 Januari gratis jika dibayar untuk jangka waktu enam bulan, Anda dapat memesan di sini .

Dell R730xd 2 kali lebih murah? Hanya kami yang memiliki 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV dari $ 249 di Belanda dan Amerika Serikat! Baca tentang Cara Membangun Infrastruktur Bldg. kelas menggunakan server Dell R730xd E5-2650 v4 seharga 9.000 euro untuk satu sen?