Matematikawan amatir menemukan cakupan universal terkecil

Melalui perhitungan geometris yang sulit, Philip Gibbs menemukan lapisan terkecil yang diketahui untuk segala bentuk yang mungkin.

Penutup universal seperti segi enam dapat dijelaskan di sekitar bentuk apa pun.

Philip Gibbs bukan ahli matematika profesional. Karena itu, ketika dia ingin merenungkan suatu tugas, dia mencari tugas yang bisa ditangani seorang amatir. Dia menemukan tugas yang sulit yang bahkan dapat membuat pikiran terbaik menjadi gila. Dan dalam sebuah makalah yang diterbitkan tahun ini, Gibbs membuat kemajuan yang signifikan dalam menyelesaikan masalah seratus tahun yang lalu, tergantung pada kemampuan untuk secara akurat mengukur area ke skala atom.

Yang pertama mengusulkan masalah ini adalah ahli matematika Prancis Henri Leon Lebesgue, dalam sepucuk surat kepada temannya Julius Pal, yang ditulis pada tahun 1914. Lebesgue bertanya: apa bentuk area terkecil yang mungkin, yang mampu sepenuhnya menutupi sejumlah besar bentuk lain (memiliki satu properti umum, yang dijelaskan di bawah)?

Selama abad yang lalu, tugas menemukan sampul universal telah berubah menjadi perangkap tikus: kemajuan dalam menyelesaikannya, jika terjadi secara berkala, selalu luar biasa kecil. Peningkatan Gibbs atas hal ini menjadi dramatis - meskipun Anda masih perlu berpikir sedikit tentangnya.

Bayangkan selusin kliping kertas berbagai ukuran dan bentuk berbaring di lantai Anda. Sekarang bayangkan Anda ditawari untuk membuat bentuk lain yang cukup besar untuk menutupi yang tersedia. Melalui eksperimen - dengan menumpangkan formulir dan membalikkannya - Anda dapat menemukan beberapa cara untuk menyelesaikan masalah ini. Tetapi, setelah menemukan cakupan universal, dapatkah Anda yakin bahwa Anda telah menemukan cakupan terkecil? Anda dapat membayangkan bahwa pada siang hari Anda secara berkala kembali ke formulir Anda, dan menemukan kesempatan untuk memotong potongan tambahan di sana-sini.

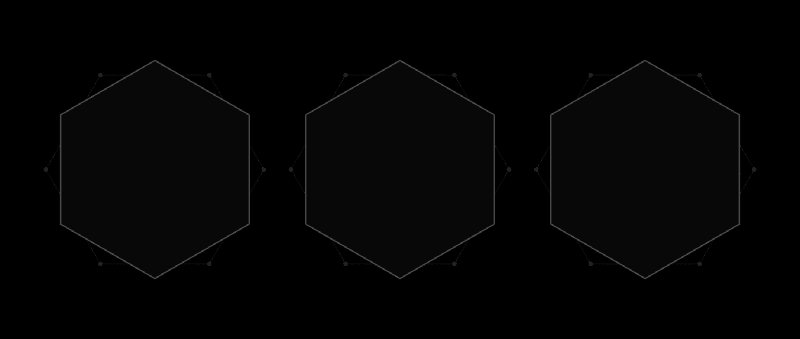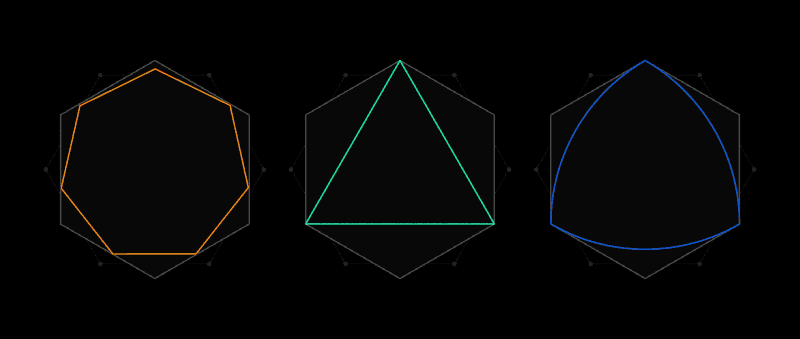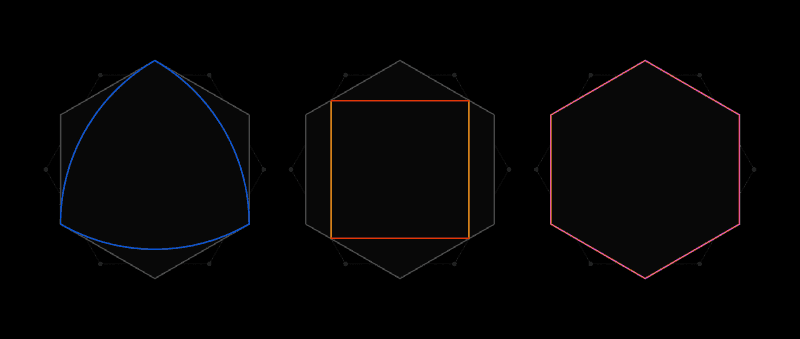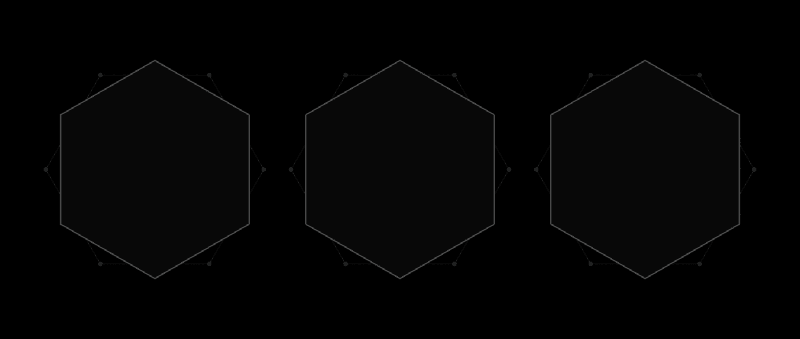
Inilah semangat masalah cakupan universal Lebesgue. Alih-alih kliping kertas, ia mempertimbangkan bentuk-bentuk di mana dua titik berjarak tidak lebih dari satu unit panjang terpisah. Bentuk yang paling jelas adalah lingkaran dengan diameter 1, tetapi ada jumlah yang tak terbatas dari mereka: segitiga sama sisi, pentagon biasa, segi enam biasa, bentuk segitiga dengan sisi bengkak, yang dikenal sebagai segitiga Röhlo - dan ini hanya untuk pemula. Berbagai bentuk membuatnya sulit untuk menemukan sampul terkecil untuk mereka semua.



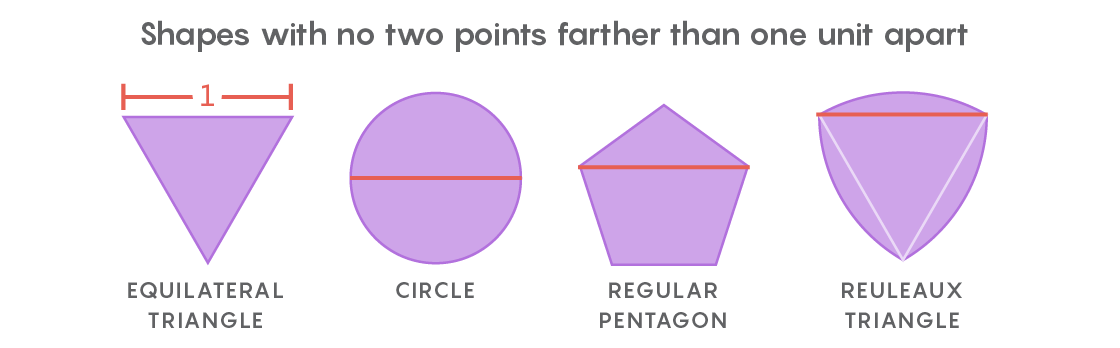
Segera setelah menerima surat dari Lebesgue, Pal menyadari bahwa segi enam reguler akan menjadi penutup universal. Dan kemudian dia meningkatkan hasil ini, mencatat bahwa dengan memotong dua sudut segi enam, tidak berdiri berdampingan, Anda bisa mendapatkan bentuk dengan area yang lebih kecil, yang masih akan berubah menjadi lapisan universal.

"Ambil segi enam, letakkan yang kedua di atasnya, putar 30 derajat, dan potong dua sudut. Di situlah Pal menyelesaikan penelitian, "kata Gibbs.

Dalam 80 tahun ke depan, dua matematikawan lain memotong strip sempit dari sampul universal Pal. Pada tahun 1936, Roland Sprag mengeluarkan sepotong kecil di sebelah salah satu sudut. Pada tahun 1992, Hansen akan menghapus dua irisan mini dari sudut kanan dan kiri bawah. Ilustrasi Hansen dapat menyampaikan lokasi bagian-bagian ini, tetapi tidak dengan ukurannya: luasnya adalah 0,00000000004 unit.



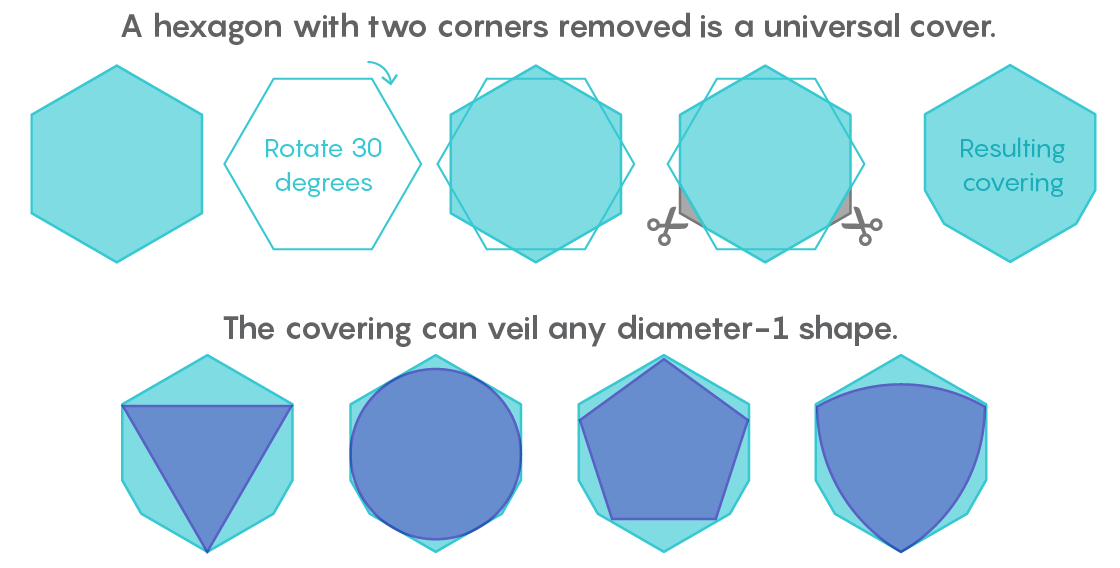
"Anda tidak dapat menggambar mereka pada skala, mereka akan menjadi ukuran atom," kata John Baez , seorang ahli matematika di University of California di Riverside.

Baez mengambil tugas Lebesgue dari dilupakan ketika ia menulis tentang hal itu di blog-nya tentang matematika populer pada 2013. Dia mengakui bahwa dia terpesona dengan tugas ini sehingga video dengan serangga yang tenggelam bisa membuat Anda terpesona. "Ketertarikan saya pada tugas itu tidak sehat," tulis BAez. "Saya tidak tahu alasan mengapa itu mungkin penting." Saya tidak melihat bagaimana ia dapat terhubung dengan banyak tugas luar biasa lainnya. Tampaknya sangat kompleks dibandingkan dengan kesan pertama. Saya mengagumi orang-orang yang mengerjakannya sama seperti saya mengagumi orang-orang yang memutuskan untuk melintasi Antartika dengan ski. ”

Philip Gibbs tidak pernah melintasi Antartika dengan ski, tetapi membaca blog Baez. Ketika dia bertemu dengan catatan masalah Lebesgue, dia berpikir: "Ya, itulah yang saya butuhkan."

Gunting atom

Gibbs pernah berpikir dia bisa menjadi ilmuwan. Dia menerima diploma dalam matematika dari University of Cambridge dan doktor dalam fisika teoretis dari University of Glasgow. Namun, ia segera kehilangan antusiasme untuk penelitian akademik dan menjadi seorang programmer. Dia bekerja pada sistem untuk desain kapal, manajemen lalu lintas udara, dan keuangan, dan pada tahun 2006 pensiun.

Gibbs tetap tertarik pada masalah akademik, tetapi sebagai peneliti awam ia tidak bisa berbuat banyak. "Sulit bagi ilmuwan independen untuk melacak apa yang terjadi," katanya. "Tetapi jika Anda menemukan ceruk yang tepat, Anda dapat melakukan sesuatu dan mendapatkan hasil yang bermanfaat."


Ahli Matematika Amatir, Philip Gibbs

Ceruk seperti itu adalah masalah cakupan universal Lebesgue. Tugas ini tidak pernah mendapat perhatian matematikawan, jadi dia curiga bahwa dia dapat mencapai beberapa kemajuan. Gibbs juga menyadari bahwa pengalaman pemrogramannya bisa menjadi keuntungan. "Saya selalu mencari masalah di mana komputer dan matematika eksperimental dapat digunakan," katanya.

Pada tahun 2014, Gibbs menjalankan simulasi komputer untuk 200 bentuk acak diameter 1. Dari simulasi, itu berarti bahwa ia mungkin dapat memotong sepotong kecil dari sudut atas penutup terkecil sebelumnya. Dia mengubah ini menjadi bukti bahwa lapisan baru akan bekerja untuk semua kemungkinan bentuk diameter 1. Gibbs mengirim bukti ke Baez, yang, bersama dengan salah seorang muridnya, Karina Baghdasaryan, membantu Gibbs memberikan karya itu gaya matematika formal.

Mereka bertiga menerbitkan karya mereka di Internet pada Februari 2015. Ini mengurangi area jangkauan universal sekecil mungkin dari 0,8441377 menjadi 0,8441153 unit. Penghematan 0,0000224 unit hampir satu juta kali lebih besar dari apa yang dicapai Hansen pada tahun 1992.

Gibbs yakin bahwa dia dapat meningkatkan hasilnya. Dalam sebuah karya yang diterbitkan pada bulan Oktober, ia memotong potongan lain yang relatif besar dari pelapis universal, sehingga luasnya menjadi 0,84409359 unit.



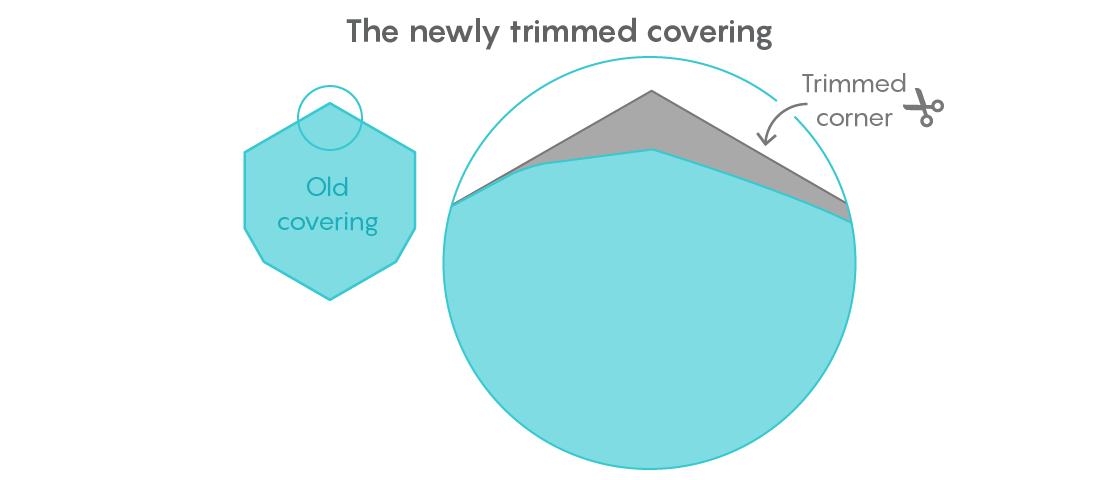
Strateginya adalah memindahkan semua bentuk dengan diameter 1 ke sudut lapisan universal yang ia temukan beberapa tahun lalu, dan kemudian menghapus seluruh area yang tersisa dari sudut yang berlawanan. Tetapi pengukuran akurat dari ruang yang dihemat terbukti sulit. Teknik yang digunakan oleh Gibbs didasarkan pada geometri Euclidean, tetapi dilakukan dengan ketelitian yang akan mengejutkan setiap siswa sekolah menengah.

“Dari sudut pandang matematika, ini semua geometri untuk sekolah menengah. Tetapi tampil dengan ketegangan fanatik, ”tulis Baez.

Sejauh ini, Gibbs menempati posisi pertama dalam mencari cakupan universal terkecil, tetapi hadiahnya dalam bahaya. Gibbs percaya bahwa ada peluang untuk menemukan cakupan yang lebih kecil. Baez berharap bahwa perhatian yang Gibbs kembali ke masalah Lebesgue merangsang minat matematikawan lainnya. Mungkin sudah saatnya untuk mengesampingkan penguasa dan kompas dan menggunakan seluruh persenjataan matematika modern.

"Ada kemungkinan bahwa cara yang tepat untuk menyelesaikan teka-teki ini akan menggunakan ide yang sama sekali berbeda," katanya, "meskipun saya tidak tahu ide apa ini."