Akurasi kedalaman jelas

Keakuratan kedalaman adalah rasa sakit di pantat bahwa setiap programmer grafis akan cepat atau lambat menghadapi. Banyak artikel dan karya telah ditulis tentang hal ini. Dan di berbagai gim dan mesin, dan pada platform yang berbeda, Anda dapat melihat banyak format dan pengaturan berbeda untuk buffer kedalaman .

Konversi kedalaman pada GPU tampaknya tidak jelas karena cara berinteraksi dengan proyeksi perspektif, dan studi tentang persamaan tidak memperjelas situasi. Untuk memahami cara kerjanya, berguna untuk menggambar beberapa gambar.



Artikel ini dibagi menjadi 3 bagian:

1. Saya akan mencoba menjelaskan motivasi untuk transformasi kedalaman nonlinier .
2. Saya akan menyajikan beberapa grafik yang akan membantu Anda memahami bagaimana konversi kedalaman non-linear bekerja dalam berbagai situasi, secara intuitif dan visual.
3. Sebuah diskusi tentang temuan utama Pengetatan Presisi Rendering Perspektif [Paul Upchurch, Mathieu Desbrun (2012)] mengenai pengaruh kesalahan titik apung pada akurasi kedalaman.

Kenapa 1 / z?

Buffer kedalaman GPU perangkat keras biasanya tidak menyimpan representasi linear jarak antara objek dan kamera, bertentangan dengan apa yang diharapkan secara naif dari objek tersebut pada pertemuan pertama. Sebaliknya, buffer kedalaman menyimpan nilai yang berbanding terbalik dengan kedalaman ruang tampilan. Saya ingin menggambarkan secara singkat motivasi untuk keputusan seperti itu.

Dalam artikel ini, saya akan menggunakan d untuk merepresentasikan nilai yang disimpan dalam buffer kedalaman (dalam kisaran [0, 1] untuk DirectX), dan z untuk mewakili ruang tampilan kedalaman, yaitu. Jarak sebenarnya dari kamera, dalam satuan dunia, misalnya meter. Secara umum, hubungan di antara mereka memiliki bentuk berikut:



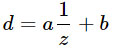
di mana a, b adalah konstanta yang terkait dengan pengaturan dekat dan jauh dari pesawat. Dengan kata lain, d selalu merupakan transformasi linear dari 1 / z .

Pada pandangan pertama, sepertinya fungsi z dapat diambil sebagai d . Jadi mengapa dia terlihat seperti itu? Ada dua alasan utama untuk ini.

Pertama, 1 / z secara alami cocok dengan proyeksi perspektif. Dan ini adalah kelas transformasi yang paling dasar, yang dijamin untuk menjaga garis. Oleh karena itu, proyeksi perspektif cocok untuk rasterisasi perangkat keras, karena tepi lurus segitiga tetap lurus di layar. Kita bisa mendapatkan transformasi linear dari 1 / z , mengambil keuntungan dari divisi perspektif yang sudah dilakukan GPU:



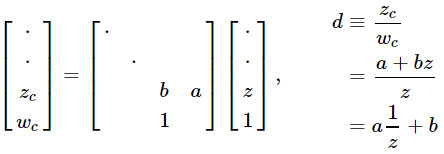
Tentu saja, kekuatan sebenarnya dari pendekatan ini adalah bahwa matriks proyeksi dapat dikalikan dengan matriks lain, memungkinkan Anda untuk menggabungkan banyak transformasi menjadi satu.

Alasan kedua adalah bahwa 1 / z linear dalam ruang layar, seperti yang dicatat Emil Persson . Ini membuatnya mudah untuk menginterpolasi d dalam segitiga selama rasterisasi, dan hal-hal seperti buffer Z hirarkis , Z-culling awal dan buffer kedalaman kompresi .

Bagan Kedalaman

Persamaan itu rumit, mari kita lihat beberapa gambar!



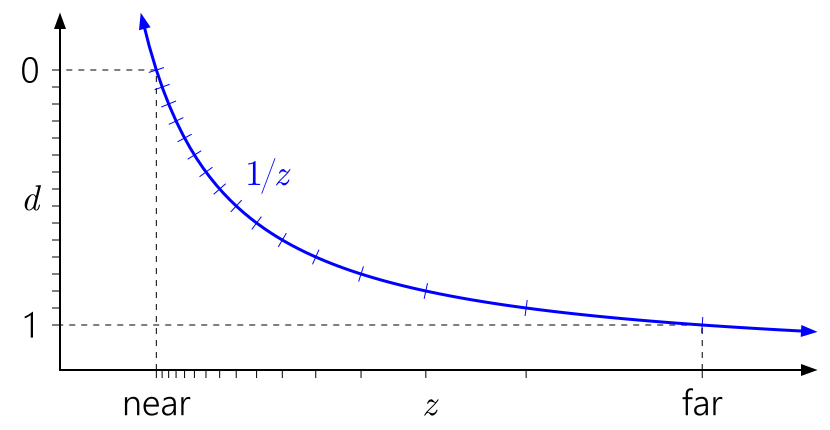
Cara membaca grafik ini dari kiri ke kanan, lalu ke bawah. Mulai dengan d pada sumbu kiri. Karena d dapat berupa transformasi linear sewenang-wenang dari 1 / z , kita dapat mengatur 0 dan 1 di tempat yang nyaman pada sumbu. Tanda menunjukkan nilai buffer kedalaman yang berbeda. Untuk tujuan kejelasan, saya memodelkan penyangga kedalaman dinormalisasi 4-bit integer, jadi ada 16 tanda spasi yang sama.

Grafik di atas menunjukkan konversi kedalaman vanila "standar" ke D3D dan API serupa. Anda dapat segera melihat bagaimana, karena kurva 1 / z , nilai-nilai yang dekat dengan bidang yang dekat dikelompokkan, dan nilai-nilai yang dekat dengan bidang yang jauh tersebar.

Juga mudah untuk memahami mengapa dekat pesawat sangat mempengaruhi akurasi kedalaman. Jarak di dekat bidang akan menyebabkan peningkatan cepat dalam nilai-nilai d relatif terhadap nilai-nilai z , yang akan mengarah pada distribusi nilai yang bahkan lebih tidak rata:



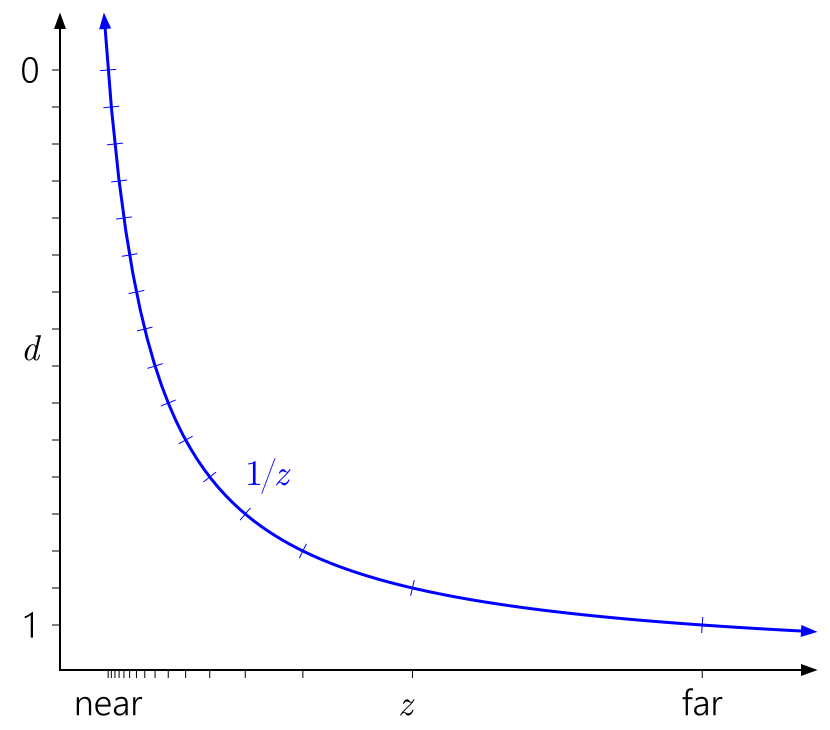
Demikian pula, dalam konteks ini, mudah untuk melihat mengapa memindahkan pesawat jauh ke tak terhingga tidak memiliki efek yang begitu besar. Itu hanya berarti memperluas rentang d ke 1 / z = 0 :



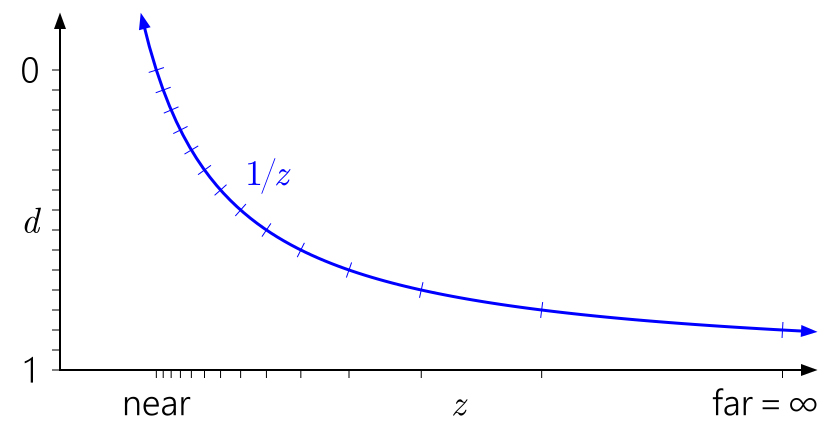
Tapi bagaimana dengan kedalaman floating-point? Grafik berikut telah ditambahkan tanda yang sesuai dengan format float dengan 3 bit eksponen dan 3 bit mantissa:



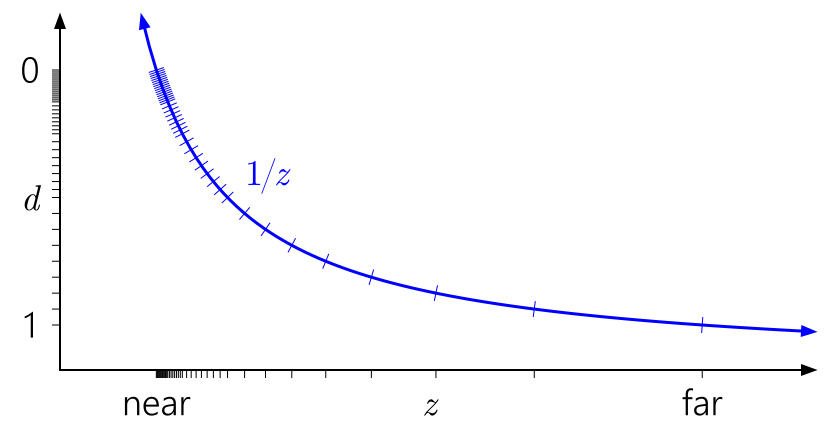
Sekarang dalam kisaran [0,1] ada 40 nilai yang berbeda - sedikit lebih dari 16 nilai sebelumnya, tetapi kebanyakan dari mereka tidak berguna dikelompokkan dekat dengan pesawat dekat (mendekati 0 float memiliki akurasi lebih tinggi), di mana kita benar-benar tidak membutuhkan banyak akurasi.

Sekarang trik terkenal adalah membalikkan kedalaman, menampilkan bidang dekat pada d = 1 dan bidang jauh pada d = 0 :



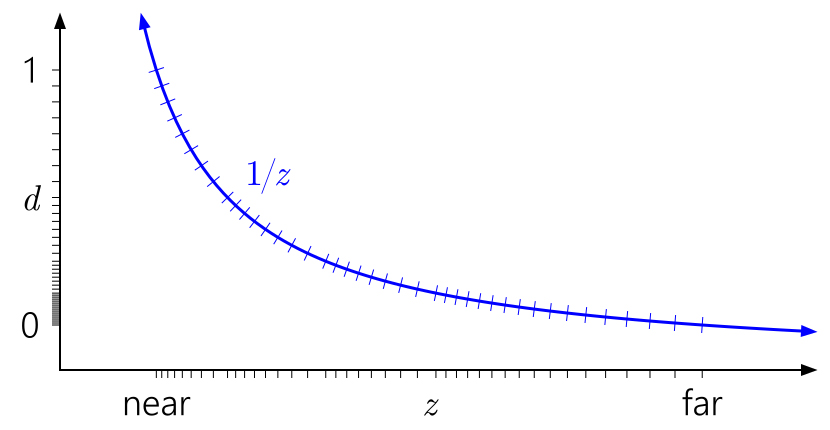
Jauh lebih baik! Sekarang distribusi quasi-logaritmik dari float entah bagaimana mengompensasi non-linearitas 1 / z , sementara lebih dekat ke pesawat dekat itu memberikan akurasi yang mirip dengan buffer kedalaman bilangan bulat, dan memberikan akurasi yang lebih besar di tempat lain. Akurasi kedalaman menurun dengan sangat lambat jika Anda bergerak lebih jauh dari kamera.

Trik terbalik-Z mungkin telah ditemukan kembali secara independen beberapa kali, tetapi setidaknya yang pertama disebutkan dalam makalah SIGGRAPH '99 [Eugene Lapidous dan Guofang Jiao (sayangnya tidak tersedia untuk umum)]. Dan baru-baru ini, ia disebutkan kembali di blog oleh Matt Petineo dan Brano Kemen , dan dalam pidato oleh Emil Persson Making Vast Game Worlds SIGGRAPH 2012.

Semua grafik sebelumnya mengasumsikan kisaran kedalaman [0,1] setelah proyeksi, yang merupakan konvensi dalam D3D. Bagaimana dengan OpenGL ?



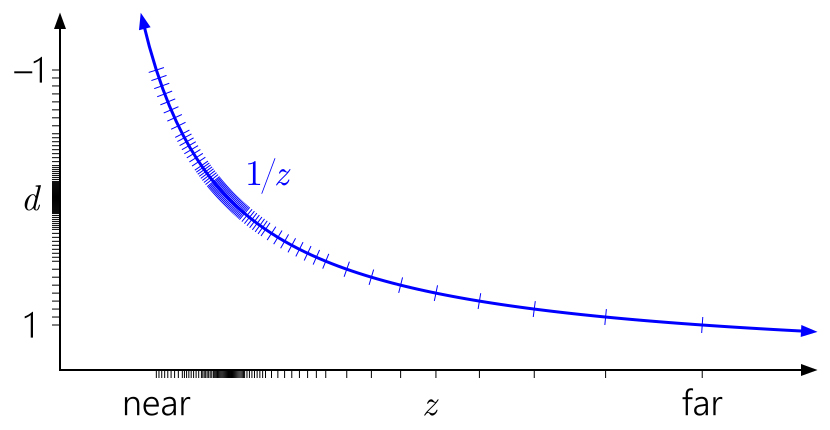OpenGL secara default mengasumsikan kisaran kedalaman [-1, 1] setelah proyeksi. Untuk format integer, tidak ada yang berubah, tetapi untuk floating-point semua akurasi terkonsentrasi tidak berguna di tengah. (Nilai kedalaman dipetakan ke kisaran [0,1] untuk penyimpanan selanjutnya di buffer kedalaman, tetapi ini tidak membantu, karena pemetaan awal ke [-1,1] telah menghancurkan semua akurasi di separuh jauh rentang.) Dan karena simetri, triknya terbalik-Z tidak akan berfungsi di sini.

Untungnya, di desktop OpenGL, ini dapat diperbaiki menggunakan ekstensi ARB_clip_control yang didukung secara luas (juga dimulai dengan OpenGL 4.5, glClipControl adalah standar ). Sayangnya, GL ES sedang dalam penerbangan.

Efek kesalahan pembulatan

Konversi 1 / z dan pilihan float vs int depth buffer adalah bagian besar dari kisah akurasi, tetapi tidak semua. Bahkan jika Anda memiliki akurasi kedalaman yang cukup untuk mewakili adegan yang ingin Anda render, mudah untuk menurunkan akurasi dengan kesalahan aritmatika selama proses konversi vertex.

Di awal artikel, disebutkan bahwa Upchurch dan Desbrun mempelajari masalah ini. Mereka mengusulkan dua rekomendasi utama untuk meminimalkan kesalahan pembulatan:

1. Gunakan pesawat jauh tak terbatas.
2. Jauhkan matriks proyeksi terpisah dari matriks lain, dan terapkan itu sebagai operasi terpisah di vertex shader, daripada menggabungkannya dengan view matrix.

Upchurch dan Desbrun membuat rekomendasi ini menggunakan metode analitis berdasarkan pemrosesan kesalahan pembulatan sebagai kesalahan acak kecil yang disajikan dalam setiap operasi aritmatika dan melacaknya ke urutan pertama dalam proses konversi. Saya memutuskan untuk menguji hasilnya dalam praktik.

Sumber di sini adalah Python 3.4 dan numpy. Program ini bekerja sebagai berikut: urutan titik acak dihasilkan, diurutkan berdasarkan kedalaman, terletak secara linear atau logaritmik antara pesawat dekat dan jauh. Kemudian poin dikalikan dengan matriks tampilan dan proyeksi dan pembagian perspektif dilakukan, menggunakan float 32-bit, dan secara opsional hasil akhir dikonversi ke int 24-bit. Pada akhirnya, ia melewati urutan dan menghitung berapa kali 2 titik tetangga (yang awalnya memiliki kedalaman berbeda) menjadi identik, karena mereka memiliki kedalaman yang sama atau urutannya berubah sama sekali. Dengan kata lain, program ini mengukur frekuensi terjadinya kesalahan perbandingan kedalaman - yang terkait dengan masalah seperti pertempuran Z - dalam berbagai skenario.

Berikut adalah hasil untuk dekat = 0,1, jauh = 10K, dengan kedalaman linier 10K. (Saya mencoba interval kedalaman logaritmik dan rasio dekat / jauh lainnya, dan meskipun angka-angka spesifik bervariasi, tren umum dalam hasilnya adalah sama.)

Dalam tabel, "eq" - dua titik dengan kedalaman terdekat mendapatkan nilai yang sama di buffer kedalaman, dan "swap" - dua titik dengan kedalaman terdekat ditukar.

	Matriks proyeksi-tampilan komposit		Matriks tampilan dan proyeksi terpisah
	float32	int24	float32	int24
Nilai Z tidak berubah (uji kontrol)	0% persamaan 0% swap	0% persamaan 0% swap	0% persamaan 0% swap	0% persamaan 0% swap
Proyeksi standar	45% eq 18% swap	45% eq 18% swap	77% eq 0% swap	77% eq 0% swap
Jauh tak terhingga	45% eq 18% swap	45% eq 18% swap	76% eq 0% swap	76% eq 0% swap
Terbalik z	0% persamaan 0% swap	76% eq 0% swap	0% persamaan 0% swap	76% eq 0% swap
Infinite + terbalik-Z	0% persamaan 0% swap	76% eq 0% swap	0% persamaan 0% swap	76% eq 0% swap
Standar + gaya GL	56% persamaan 12% swap	56% persamaan 12% swap	77% eq 0% swap	77% eq 0% swap
Infinite + GL-style	59% persamaan 10% swap	59% persamaan 10% swap	77% eq 0% swap	77% eq 0% swap

Saya minta maaf atas kenyataan bahwa tanpa grafik, ada terlalu banyak dimensi di sini dan tidak dapat membuatnya! Bagaimanapun, melihat angka-angka, kesimpulan berikut jelas:

• Dalam kebanyakan kasus, tidak ada perbedaan antara buffer kedalaman int dan float . Kesalahan aritmatika untuk menghitung kedalaman menimpa kesalahan dalam konversi ke int. Sebagian karena float32 dan int24 memiliki ULP yang hampir sama (satuan akurasi paling rendah adalah jarak ke nomor tetangga terdekat) sebesar [0,5.1] (karena float32 memiliki mantissa 23-bit), sehingga kesalahan konversi tidak ditambahkan ke hampir seluruh rentang kedalaman. di int.
• Dalam kebanyakan kasus, pemisahan pandangan dan matriks proyeksi (mengikuti rekomendasi Upchurch dan Desbrun) meningkatkan hasilnya. Terlepas dari kenyataan bahwa tingkat kesalahan keseluruhan tidak menurun, "swap" menjadi nilai yang sama, dan ini merupakan langkah ke arah yang benar.
• Infinite far plane sedikit mengubah frekuensi kesalahan. Upchurch dan Desbrun memperkirakan pengurangan 25% dalam frekuensi kesalahan numerik (kesalahan akurasi), tetapi ini tampaknya tidak mengarah pada penurunan frekuensi kesalahan perbandingan.

Namun, temuan di atas tidak nyata dibandingkan dengan sihir terbalik-Z . Periksa:

• Reversed-Z dengan buffer kedalaman mengambang memberikan tingkat kesalahan nol dalam pengujian. Sekarang, tentu saja, Anda bisa mendapatkan beberapa kesalahan jika Anda terus meningkatkan interval nilai kedalaman input. Namun, Z terbalik dengan float jauh lebih akurat daripada opsi lainnya.
• Reversed-Z dengan buffer kedalaman integer sama baiknya dengan opsi integer lainnya.
• Reversed-Z mengaburkan perbedaan antara komposit dan pandangan terpisah / proyeksi matriks, dan pesawat jauh terbatas dan tak terbatas. Dengan kata lain, dengan Z terbalik, Anda dapat melipatgandakan proyeksi dengan matriks lain, dan menggunakan pesawat jauh yang Anda inginkan, tanpa mengurangi akurasi.

Kesimpulan

Saya pikir kesimpulannya jelas. Dalam situasi apa pun, ketika berhadapan dengan proyeksi perspektif, cukup gunakan buffer kedalaman mengambang dan terbalik-Z ! Dan jika Anda tidak dapat menggunakan buffer kedalaman float, Anda masih harus menggunakan Z terbalik. Ini bukan obat mujarab untuk semua penyakit, terutama jika Anda menciptakan lingkungan dunia terbuka dengan rentang kedalaman ekstrem. Tapi ini awal yang bagus.