
Halo, Habr! Nama saya Akhmadeev Rinat, saya Sr. Pengembang PHP.
Saya berikan kepada Anda ringkasan laporan Buat kata sandi menjadi luar biasa lagi! Cara mengalahkan bruteforce dan meninggalkan peretas tanpa apa pun dari Alexey Ermishkin dari Virgil Security dengan HighLoad ++ 2018 .
Ketika saya pergi ke laporan, saya pesimis. Tapi sejak itu Karena ini adalah Virgil Security, saya masih memutuskan untuk pergi. Pada awalnya, laporan itu tampaknya benar-benar milik kapten, dan saya bahkan mulai kehilangan minat, tetapi kemudian, ternyata, saya bahkan menemukan beberapa pendekatan perlindungan kata sandi baru yang berbeda dari hashing garam biasa.
Laporan ini membahas cara untuk melindungi kata sandi dari hash ke pendekatan yang lebih modern, seperti kata sandi Facebook Bawang, Sphinx dan Pythia. Pada akhirnya, Layanan Enkripsi Hardened Enkripsi Sederhana (PHE) baru diperkenalkan.
Saya sangat menyukai laporan itu sehingga saya menyiapkan ringkasan. Saya merekomendasikan semua orang untuk membiasakan diri.
Alexey Ermishkin membagikan slide dan laporan video dalam komentar:
Abstrak
Entri

Halo semuanya, selamat pagi semuanya! Saya senang melihat Anda semua di Konferensi Highload. Nama saya Alexey Ermishkin, saya bekerja untuk Virgil Security.

Kami terlibat dalam pengembangan berbagai produk kriptografi untuk pengembang individu dan bisnis. Kami fokus pada solusi end-to-end, ini adalah saat Anda tidak perlu mempercayai layanan untuk melakukan tindakan seperti transfer data, otentikasi, dll. SDK kami terbuka dan dapat diakses oleh semua.
Kata sandi telah lama digunakan sebagai sarana otentikasi, sebagai cara untuk mencapai suatu tempat. Itu jauh sebelum komputer muncul. Tetapi dengan munculnya komputer, dengan munculnya sistem IT, orang tidak meninggalkan kebiasaan menggunakan kata sandi. Ini menjadi masalah yang sangat besar bagi pengembang, karena mereka mengalami masalah bagaimana membuat sistem yang nyaman dan cepat dan aman. Sangat sering, ketika beberapa dari aspek-aspek ini berusaha untuk melakukannya dengan baik, yang ketiga tidak terlalu baik. Jika Anda membuat sistem ini produktif dan aman, maka itu bisa merepotkan, dll.

Jadi, apa yang akan kita bicarakan hari ini?
Saya akan berbicara tentang perlindungan terhadap serangan offline. Ketika kata sandi masuk ke dalam basis data Anda, maka pengguna tidak mengontrolnya. Jika basis data Anda diretas, ia bocor di suatu tempat, lalu setelah itu peretas dapat melakukan apa saja dengan itu. Bahkan jika Anda entah bagaimana melindungi kata sandi, mereka dapat mulai memilahnya dan mereka tidak perlu berinteraksi dengan siapa pun untuk ini, mereka sudah memiliki segalanya untuk ini. Selain itu, pengguna tidak berhenti menggunakan kata sandi yang lemah. Kebijakan kata sandi tentu saja merupakan hal yang bermanfaat, tetapi juga tidak selalu nyaman, mis. bahkan ketika orang-orang memasukkannya sebagai kata sandi yang kuat, kebijakan itu masih mengatakan Anda perlu menambahkan huruf atau angka, maka bagi mereka itu tidak nyaman. Jelas juga bahwa masalahnya adalah kebutuhan untuk membandingkan apa yang dimasukkan pengguna dengan apa yang Anda miliki dalam database. Bagaimana cara melakukannya dengan cara yang aman? Nah, jangan lupa bahwa di dalam perusahaan ada juga orang-orang yang tidak sepenuhnya ramah dan ingin melindungi diri mereka dari mereka juga.
Hash
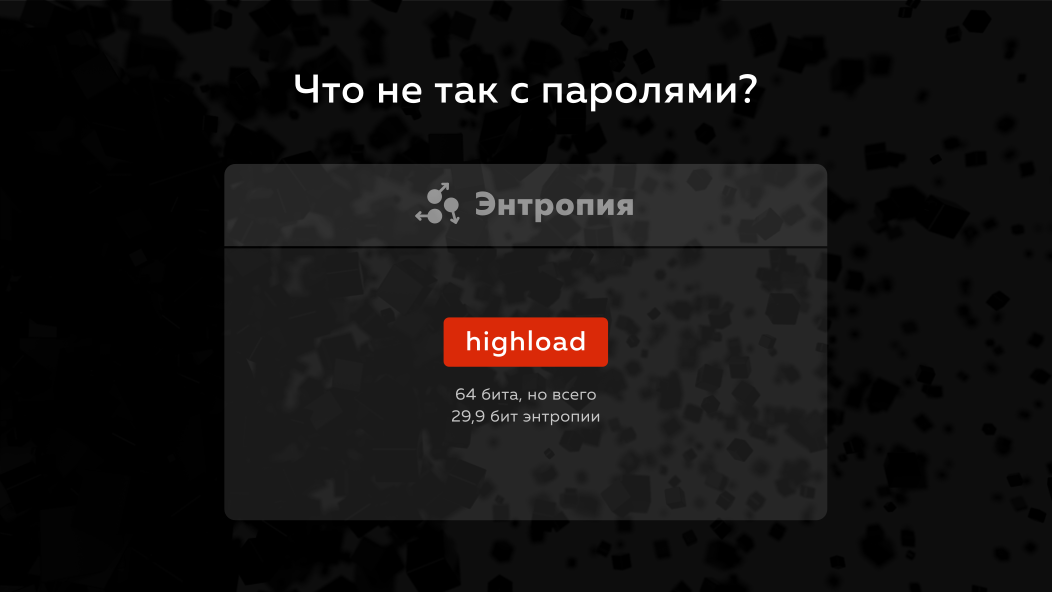
Pada prinsipnya, mengapa kata sandi adalah subjek yang sangat menyakitkan, mengapa perlu bekerja dengan mereka dengan lebih hati-hati? Masalahnya adalah bahwa kata sandi memiliki entropi kecil. Apa itu entropi? Ini adalah jumlah informasi yang terkandung dalam data, mis. misalnya, dalam kata Highload 8 huruf adalah 8 byte, tetapi jika kita menghitung entropi, itu tidak akan menjadi 64 bit seperti seluruh kata, tetapi kurang dari 30 bit. Ketika hari ini mereka berbicara tentang memecahkan kata sandi, mereka mengatakan bahwa adalah mungkin untuk memecahkan kata sandi dengan entropi dalam waktu seperti itu, tidak ada lagi atau tidak kurang dari begitu banyak bit. Yaitu bahkan jumlah kata sandi tidak diperhitungkan.

Bagaimana orang memulai dengan keamanan kata sandi? Hal pertama yang terlintas dalam pikiran adalah menggunakan hash kriptografi searah.

Fitur luar biasa mereka adalah bahwa mereka tidak dapat dikembalikan. Yaitu Jika Anda mentransfer beberapa informasi ke hash ini, menerima nilai pada output, Anda tidak bisa mendapatkan informasi ini kembali dari nilai ini. Namun, sayangnya, perhitungannya sangat cepat. Misalnya, sekelompok kartu grafis NVidia 4 modern dapat memproses beberapa miliar kata sandi per detik. Yaitu jika entropi kata sandi Anda kurang dari 40 bit, maka sekelompok 4 kartu video akan mengambilnya di sana dalam satu menit, atau bahkan kurang.
Meja pelangi

Selain itu, setiap hash yang rumit memiliki tabel pelangi sendiri. Apa meja ini dan bagaimana mereka dibuat?

Yaitu mereka mengambil kata sandi dan kombinasi karakter paling populer yang dapat ditampung di hard drive, mempertimbangkan hash untuk mereka dan menempatkannya di beberapa penyimpanan lebih untuk beberapa terabyte. Ketika ada beberapa jenis hash, Anda tidak dapat menghitungnya, tetapi menemukannya sangat cepat dari tabel ini dan membandingkannya dengan kata sandi yang sebelumnya dihitung. Yaitu Keuntungan dari tabel adalah bahwa mereka bekerja sangat cepat, tetapi Anda membutuhkan banyak ruang untuk menyimpannya. Namun demikian, ada tabel untuk hash paling populer di Internet, dapat diunduh, atau bahkan dibeli.
Catatan penulis sinopsis: Wikipedia tidak setuju dengan pembicara: "Rainbow table adalah versi khusus dari tabel pencarian untuk membalikkan fungsi hash kriptografi menggunakan mekanisme kompromi yang masuk akal antara waktu pencarian dalam tabel dan memori yang ditempati." Yaitu itu tidak menyimpan hash dari kata sandi paling populer yang akan muat di disk, tetapi hanya hash dari beberapa kata sandi, sisanya dihitung berdasarkan kata-kata yang ada - ada beberapa kata sandi per catatan dalam tabel.
Garam

Tetapi sekali lagi, setiap meja pelangi memiliki garam sendiri. Apa itu garam? Ini adalah serangkaian byte acak, yang ditambahkan ke kata sandi. Itu disimpan di meja di suatu tempat dekat hash dan melindungi dari tabel pelangi.

Yaitu orang-orang yang mendapatkan tangan mereka dengan hash asin masih harus menghitung hash ini. Tetapi masalahnya adalah bahwa hash ini dihitung dengan sangat cepat dan garam tidak banyak membantu di sini.
Bagaimana cara memperlambat pencarian?

Cara alami dari ini bisa memperlambat pengurutan hash dalam beberapa cara. Bagaimana ini bisa dilakukan?

Pendekatan yang paling naif adalah bahwa kita mengambil semacam fungsi hash, misalnya sha256, dan menghitungnya secara iteratif, mis. hitung hash, dari hash ini hash lagi, dll. Anda dapat melakukan ini ribuan bahkan jutaan kali. Masalahnya adalah bahwa jika Anda menulis sendiri implementasi seperti itu, maka kemungkinan besar akan lebih lambat daripada implementasi orang yang secara profesional terlibat dalam menebak kata sandi.

SCrypt , Bcrypt , Argon2
Dan oleh karena itu, cryptographers memunculkan beberapa fungsi yang secara khusus dirancang untuk memperlambat pencarian kata sandi - mereka menggunakan sejumlah besar memori dan semua kemungkinan instruksi prosesor modern. Jika kata sandi yang dilindungi oleh fungsi seperti itu jatuh ke tangan penyerang, maka mereka harus menggunakan perangkat keras yang sangat kuat.

Sebagai contoh, fungsi Argon2 paling modern berfungsi sebagai berikut: pada diagram Anda dapat melihat bahwa ada banyak blok memori berbeda yang digunakan untuk menjalankan hash. Dia melakukan ini dengan berbagai cara pulang pergi, memori digunakan dengan sangat intensif, seluruh memori digunakan. Agak sulit untuk mengoptimalkan fungsi seperti itu (kecepatan pencarian).

Namun pendekatan ini juga memiliki kelemahan. Fungsi-fungsi ini dibuat lambat secara khusus, tetapi mereka secara khusus lambat tidak hanya untuk penyerang, mereka akan sangat lambat untuk Anda juga. Mereka akan memuat besi Anda. Fungsi-fungsi ini dapat disesuaikan, mis. Anda dapat memilih berapa banyak memori yang akan digunakan untuk menghitung hash dari satu kata sandi, hingga beberapa gigabytes, berapa banyak yang melewati memori ini. Jika Anda memutar parameter ini dengan sangat serius, perangkat keras Anda sendiri akan rusak dan jika Anda memiliki banyak orang yang masuk ke sistem, maka Anda hanya perlu mengalokasikan sumber daya yang cukup besar untuk perlindungan kata sandi dan kata sandi sederhana, yah, kata sandi yang sangat sederhana masih dapat diambil. .
Kata sandi Facebook Bawang

Orang-orang memikirkan hal ini dan mengajukan pertanyaan: apakah mungkin untuk mencapai properti yang sama tanpa memuat backend, tanpa memuat server mereka sendiri?

Salah satu pelopor dalam hal ini adalah Facebook . Baris-baris ini yang Anda lihat adalah tahapan historis Facebook, bagaimana mereka melindungi kata sandi, pada awalnya hanya ada kata sandi, kemudian mereka mengambil fungsi md5 lama, yang telah dipecah untuk waktu yang lama, kemudian mereka menambahkan garam di sana dan mengambil hash sha1 , dan kemudian itu terjadi Yang menarik, mereka membawa perhitungan fungsi hmac (ini adalah hash dengan kunci) ke layanan jarak jauh.
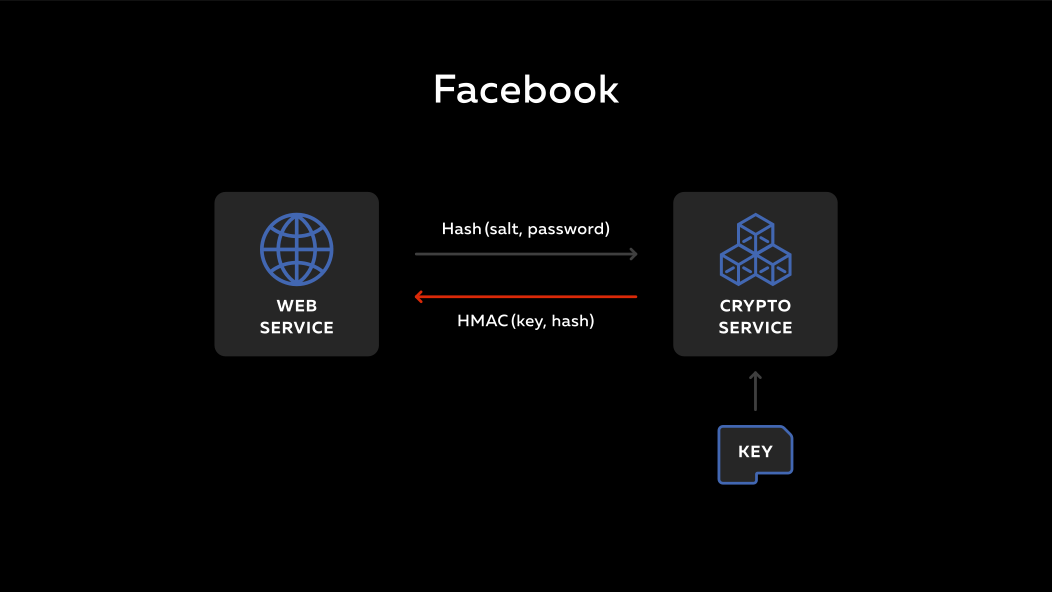
Bagaimana cara kerjanya? Ada backend, ada layanan jarak jauh. Ada semacam kunci rahasia pada layanan ini. Seseorang memasuki backend, memasukkan kata sandinya. Kata sandi ini dicampur dengan garam yang ada di database, dijalankan melalui hash dan dikirim ke layanan. Layanan mengambil kunci privatnya, menghitung fungsi hmac, dan mengirim semuanya kembali. Di backend, diletakkan di pangkalan.
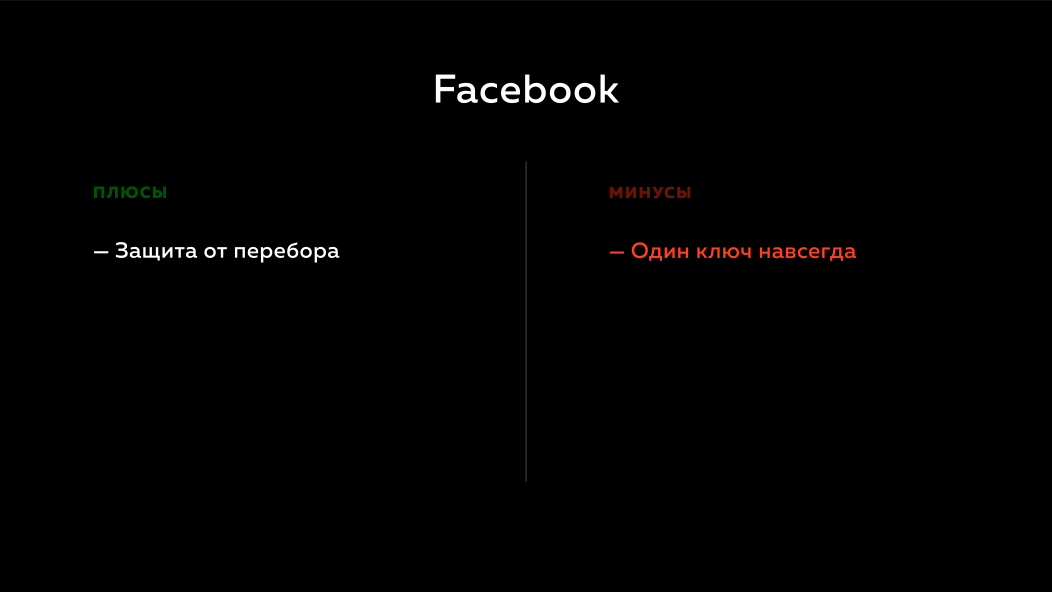
Apa yang diberikannya? Jika Facebook memiliki basis data pengguna, maka tidak layak untuk mengurutkan kata sandi di dalamnya, karena mereka tidak memiliki kunci rahasia jarak jauh. Tetapi masalah dengan pendekatan Facebook adalah jika sesuatu terjadi pada kunci pribadi jarak jauh mereka, mereka akan berada dalam masalah besar. Mereka tidak bisa berbuat apa-apa karena mereka menggunakan hash, mereka menggunakan hmac. Mereka tidak memiliki cara untuk menyelesaikan situasi ini sehingga pengguna tidak akan melihat apa-apa dan ini akan membuat mereka terpojok.
Sphinx
Cryptographers melihat semuanya. Mereka menyukai gagasan menggunakan layanan jarak jauh dan memutuskan untuk berpikir: apakah mungkin melakukan lebih baik? Apakah mungkin untuk membuat sistem yang serupa, tetapi tanpa kekurangan yang telah diberkahi oleh Facebook?

Dan mereka memutuskan untuk mendekati masalah ini sebagai berikut: bagaimana jika kata sandi atau kata sandi hash direpresentasikan sebagai angka? Jika kita memiliki kata passw0rd , kata itu terdiri dari 8 byte. Di hampir semua bahasa pemrograman, ada tipe integer delapan byte, mis. Pada prinsipnya, ini satu dan sama. Yaitu 8 byte, kata passw0rd dan kita dapat menyatakannya sebagai angka desimal biasa. Apa yang ini berikan pada kita? Ini memberi kita kebebasan bertindak yang sama sekali berbeda. Kita dapat menambahkan kata sandi atau hash dari mereka, melipatgandakannya, mengubahnya menjadi beberapa nomor lain. Kita dapat melakukan operasi matematika yang sangat serius dengan mereka.

Salah satu sistem pertama yang menggunakan teknologi ini adalah Sphinx . Dia muncul beberapa tahun yang lalu. Ini adalah pengelola kata sandi deterministik. Ada banyak program berbeda seperti keepass , di mana Anda memiliki kata sandi utama dan untuk setiap situs menghasilkan kata sandi acak. Tetapi ada juga hal-hal deterministik di mana Anda memasukkan kata sandi utama Anda, situs yang ingin Anda kunjungi dan menghitung sesuatu di sana dan mengeluarkan kata sandi unik untuk setiap situs. Tetapi jelas bahwa jika kata sandi utama ini masuk ke suatu tempat, maka semua kata sandi dari situs Anda akan dikompromikan secara permanen.
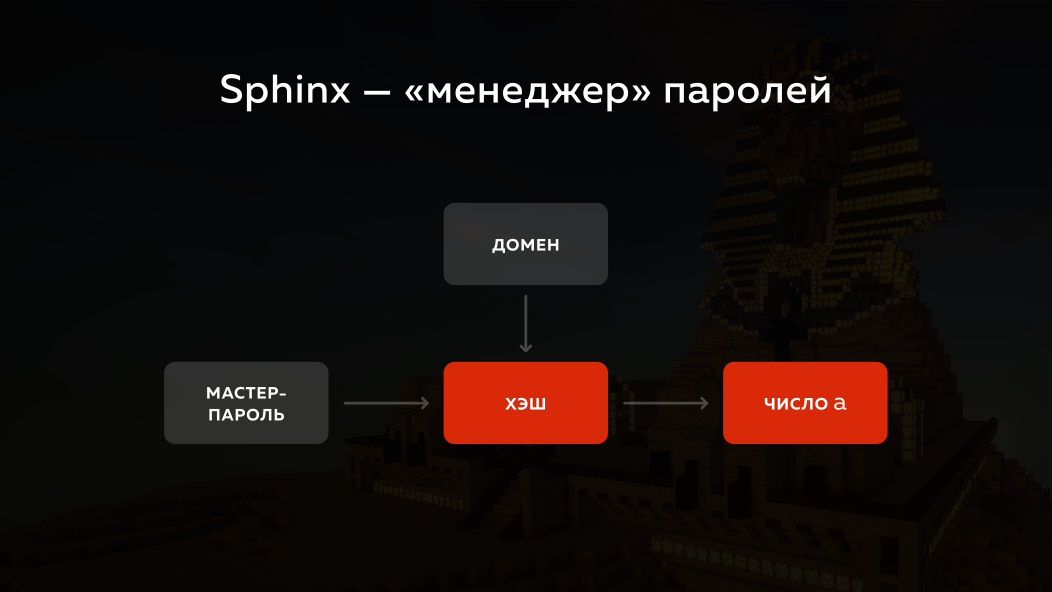
Bagaimana Sphinx mendekati masalah ini? Dia mengambil kata sandi utama, dia mengambil domain yang ingin Anda masuki, menjalankan semuanya melalui hash dan mengubahnya menjadi angka. Tetapi pada kenyataannya, kriptografi eliptik digunakan di sana, untuk kesederhanaan saya akan menjelaskan semua ini pada bilangan biasa dengan matematika biasa. Dia mengubahnya menjadi angka (sebut saja a ) dan apa yang dia lakukan selanjutnya?

Hal yang benar-benar luar biasa, setiap kali kita dapat menghasilkan angka acak r . Jika kita menaikkan bilangan a ke pangkat r , dan beberapa waktu kemudian kita menaikkan bilangan ini ke pangkat kebalikan ke b, maka kita mendapatkan kembali bilangan yang sama a , kan? Yaitu kita bisa menutupi sesuatu dari awal, dan kemudian membuka kedoknya.
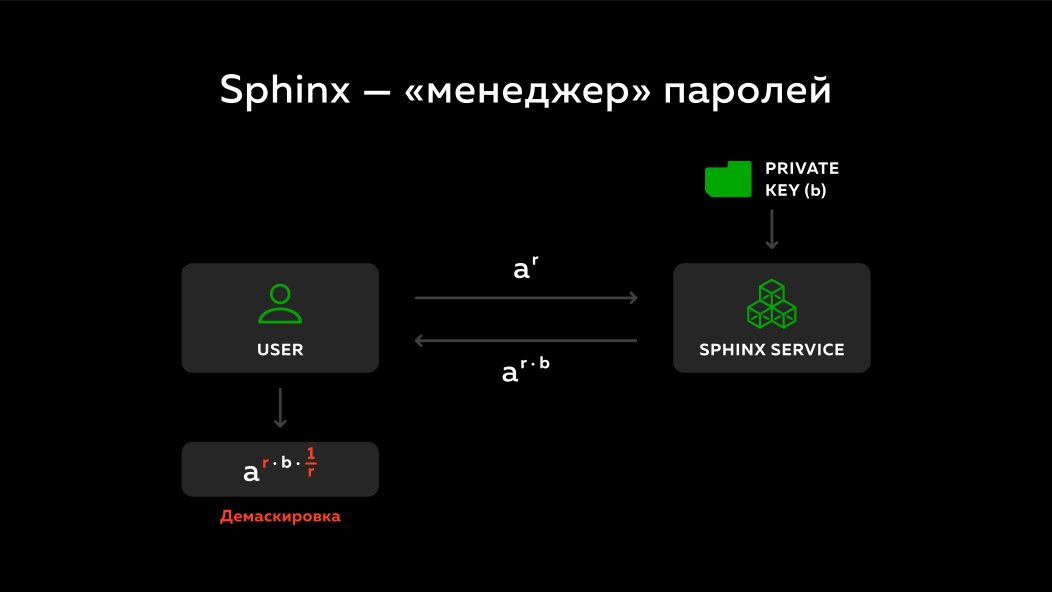
Dan apa yang dilakukan sphinx? Sekali lagi ada pengguna, ada layanan jarak jauh. Nomor bertopeng dikirim ke layanan jarak jauh ini. Pada layanan jarak jauh, ada kunci pribadi b . Apa yang dia lakukan Dia mengalikan nomor yang dikirim dengan kunci rahasianya b dan mengirimkannya kembali. ( Catatan penulis ringkasan: pada slide, jumlah yang dikirim tidak dikalikan dengan kunci privat, tetapi dinaikkan ke tingkat kunci privat, tetapi poin utamanya adalah ). Karena angka r berbeda setiap kali, layanan jarak jauh tidak dapat mengatakan apa pun tentang kata sandi dan domain mana yang di-mask, yaitu setiap kali dia melihat beberapa angka acak yang berbeda. Dan dia hanya mengalikan dengan kunci pribadinya b dan mengirim kembali.
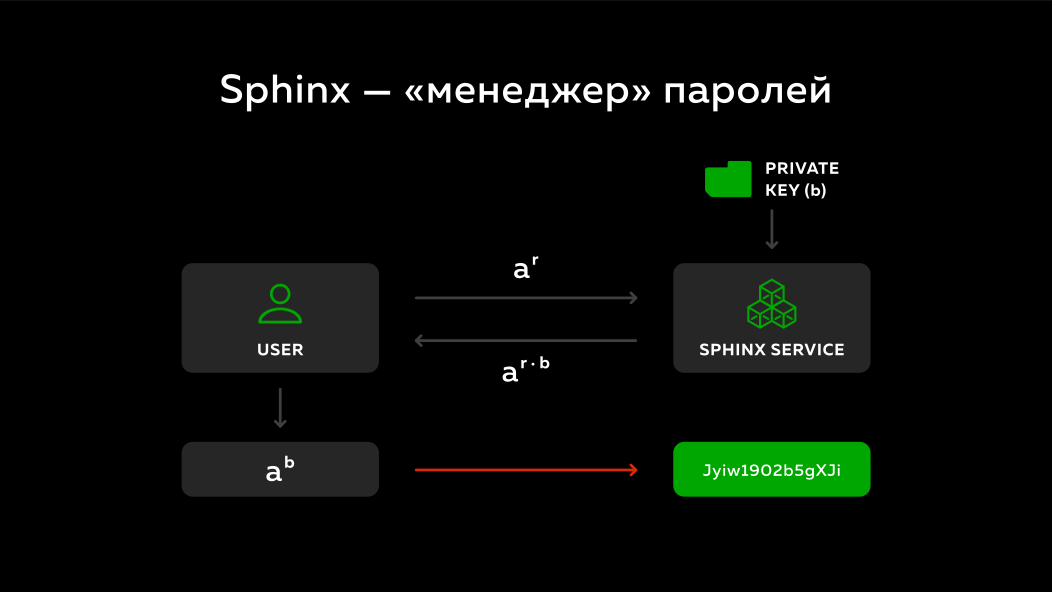
Pengguna membuka tabir apa yang dikirim oleh server kepadanya dan ia mendapatkan nomor - kata sandi masternya dengan domain dikalikan dengan kunci rahasia server a^b . Ternyata dia tidak tahu kunci rahasia server, server tidak tahu apa yang dikirim pengguna, tetapi pada akhirnya dia juga mendapat semacam nomor deterministik. Setiap kali Anda menjalankan protokol ini, penyamaran akan berbeda, tetapi hasilnya akan selalu sama dan hasil ini kemudian dapat diubah kembali menjadi semacam kata sandi dan digunakan untuk memasuki berbagai situs.

Teknologi yang benar-benar luar biasa. Pertama, Anda dapat menghasilkan kata sandi besar, mis. melindungi dari busting. Kedua, jika seorang hacker mendapatkan akses ke beberapa kata sandi, ia tidak akan dapat mengatakan apa pun tentang sisanya, karena mereka dihasilkan secara independen satu sama lain. Ketiga, jika kata sandi pengguna hilang di suatu tempat, maka ini juga tidak akan memberikan apa-apa, karena peretas tidak akan memiliki kunci rahasia. Keempat, ini bekerja sangat cepat, karena tidak ada hash besar berulang diperlukan di sini, yaitu secara harfiah 2-3 perkalian dilakukan dan semuanya bekerja secara instan.
Tetapi sistem ini memiliki kekurangan. Server yang digunakan pengguna untuk berbicara tidak tahu apa-apa tentang dirinya. Dia hanya menerima beberapa angka acak sebagai input, mengalikannya dengan sesuatu dan mengirimkannya kembali. Klien juga tidak tahu apa-apa tentang server, ia mengirim sesuatu ke suatu tempat, menerima hasilnya, ia bekerja - baik. Tetapi jika sesuatu terjadi pada layanan, pengguna tidak akan dapat mengatakan apa-apa tentang itu, ia tidak memiliki informasi untuk ini. Kunci rahasia juga tidak bisa diubah, tidak ada yang bisa dilakukan dengan itu.
Pythia

Mungkinkah ini lebih baik?

Cryptographers melihat sistem ini dan berpikir, apakah mungkin untuk meningkatkan sistem dan menambahnya dengan properti yang akan memungkinkan kita untuk mengatakan bahwa itu sesuai dengan prinsip-prinsip ujung ke ujung? Yaitu klien dapat berkomunikasi dengan server, tetapi pada saat yang sama, ia juga dapat mengotentikasi dan dapat mempercayainya sampai batas tertentu.

Dan mereka datang dengan protokol yang disebut Pythia .

Itu dibuat oleh pria hebat Adam Everspaugh dengan rekan-rekannya. Apa yang membuatnya unik? Pertama, layanan tahu siapa yang memasukkan kata sandi, yaitu ID pengguna diteruskan ke server melewati kata sandi. Ini bisa berupa kotak id acak yang terletak di sebelahnya, atau hanya nama pengguna. Itu tidak masalah. Tetapi layanan tahu tentang itu. Tetapi server tidak hanya tahu sedikit tentang ini, secara matematis dapat membuktikan bahwa itu adalah dia.

Bagaimana cara kerjanya? Ada backend (semacam layanan web, situs) dan ada layanan Pythia. Apa yang dilakukan backend dan apa yang dilakukan layanan? Ada kunci pribadi k pada layanan, tetapi juga mentransfer kunci publiknya ke backend. Backend layanan tidak hanya mengirim nomor bertopeng a^r , seperti dalam protokol Sphinx, tetapi juga mengirimkan semacam pengenal pengguna ( UserID ). Layanan ini mengalikan ID pengguna dan kata sandi dengan kunci privatnya dan hasilnya (UserID, a)^(r*k) mengirimkan backend. Dia juga mengirim kembali Proof tertentu, yang dapat digunakan oleh backend untuk memeriksa server bahwa ia belum diretas, bahwa ia merespons sebagaimana mestinya.

Lalu ada unmasking dan angka y yang hasilnya dimasukkan ke dalam DB. Dalam database kami tidak hanya memiliki hash, tetapi angka, titik kurva eliptik.

Ada beberapa poin menarik di sini:
- Kemampuan server menggabungkan ID pengguna dan kata sandi menjadi satu nomor. Ini disebut operasi bilinear atau pasangan bilinear. Ini adalah matematika yang relatif baru, yang baru-baru ini mulai digunakan. Dia memiliki semua sifat matematikawan baru dalam 30 tahun yang belum berlalu sehingga semua orang akan yakin bahwa semuanya normal dengan ini.
- Tetapi
Proof yang mengirim layanan adalah teknologi yang agak lama. Ini disebut protokol Schnorr . Generasi kunci publik adalah penggandaan titik dasar dengan beberapa kunci rahasia. Protokol Schnorr membuktikan bahwa kunci rahasia yang digunakan untuk menghasilkan kunci publik digunakan untuk mengalikan kata sandi pengguna dengan nomor yang sama. Protokol ini sudah lama ada, sudah banyak digunakan di mana dan memungkinkan Anda untuk membuktikan. Ini disebut zero-proof proof - server tidak menunjukkan kunci publiknya, tetapi dikatakan bahwa operasi yang saya lakukan dilakukan oleh kunci pribadi itu, yang semula kami sepakati.

Apa kelebihan sistem ini?

Dan dia tidak punya banyak.
- Sistem tidak memuat backend. Karena backend melakukan segalanya, itu mengubah kata sandi menjadi angka, menyamarkannya, mengirimkannya, lalu membuka kedok hasilnya.
- Jika database dengan nomor tersebut dicuri dari Anda, maka pengurutan kata sandi juga tidak masuk akal tanpa kunci pribadi.
- Layanan Pythia dapat memblokir upaya kekerasan, yang berarti backend tidak harus melakukan ini pada prinsipnya. Jika dia melihat bahwa di bawah ID pengguna yang sama mereka mencoba melakukan operasi transformasi ini beberapa kali, dia bisa memotongnya dan memblokirnya pada batas nilai.
- Berkat penyamarannya, layanan ini tidak tahu apa-apa tentang kata sandi. Setiap kali nomor acak baru dikirimkan kepadanya. Hanya pengidentifikasi pengguna yang tetap konstan.
- Berkat ZKP (Zero-knowledge proof), backend selalu tahu bahwa itu adalah layanan yang pernah ia hubungi.
- Jika Anda memiliki database dengan hashes dan garam misalnya, maka Anda dapat bermigrasi ke solusi seperti itu untuk pengguna. Mereka bahkan mungkin tidak memperhatikan apa pun. Alih-alih kata sandi pengguna, Anda mengambil hash, mengarahkannya ke Pythia dan di masa depan cukup gunakan protokol ini, dapatkan nomor
y , taruh lagi di database Anda. Hash kemudian dapat dihapus. Setiap kali pengguna login ke sistem Anda, protokol ini akan dieksekusi, beberapa nomor akan diperoleh, yang akan Anda bandingkan dengan apa yang ada di database. Sistem otentikasi itu sendiri akan tetap tidak berubah, seperti pengguna akan masuk lebih awal dan masuk, dengan kata sandi yang sama, bahkan yang lemah. Dalam hal ini, sistem akan jauh lebih aman.

Tapi ini tidak semua barang.

Salah satu fitur utama adalah bahwa bahkan jika layanan Pythia diretas, dimungkinkan untuk membuat kunci pribadi baru. Dalam database kami, nomor disimpan, bukan hash. Jika kita merepresentasikan kunci lama sebagai angka k , dan yang baru sebagai angka k' , maka kita dapat menghitung angka yang disebut token Pembaruan. Untuk melakukan ini, kami mengalikan angka baru dengan angka terbalik dengan yang lama. Dan dengan token pembaruan ini, Anda dapat pergi melalui database untuk setiap pengguna dan mengalikan angka ini dengan memperbarui token. Setelah Anda melakukan ini, sistem Anda terus bekerja dengan kunci pribadi baru pada layanan jarak jauh. Itu semua terjadi secara instan. Jika terjadi bencana, basis data Anda dengan kata sandi telah dicuri dari Anda, Anda melepaskan token pembaruan dengan mengklik jari dan fakta bahwa peretas mencuri dari Anda menjadi tidak berguna secara instan. Anda hanya diam-diam berjalan melalui semua catatan di latar belakang, memperbaruinya dan mereka bekerja dengan kunci rahasia baru untuk Anda. Pengguna umumnya bahkan tidak memperhatikan apa pun. Yaitu Pembaruan yang mulus dan pembatalan database kata sandi yang instan adalah beberapa fitur inovatif utama dari sistem ini.

Tapi itu belum semuanya.

Angka yang terletak di pangkalan besar y , pada dasarnya besar dan terlihat cukup pseudo-acak, yaitu sangat mudah untuk tidak mengambilnya. Jika kita mentransfer fungsionalitas yang kita miliki di backend, misalnya, ke perangkat klien, ke ponsel, maka kita dapat menggunakan ini untuk menghasilkan kunci. Kami menyebut hal ini BrainKey. Ini berarti bahwa pengguna memasukkan kata sandi di suatu tempat di telepon, juga menyamarkannya, mengirimkannya ke layanan jarak jauh. Layanan mengembalikan angka tertentu y dan kemudian Anda dapat menggunakan y ini untuk menghasilkan beberapa kunci asimetris. Dengan demikian, pengguna dari kata sandinya bisa mendapatkan pasangan kunci. Ini digunakan di semua jenis BrainWallets . Inilah saatnya Anda memasukkan kata sandi dan mendapatkan dompet bitcoin yang dihasilkan untuk itu. Tetapi aplikasi ini tidak terbatas pada cryptocurrency, ini adalah tanda tangan digital, beberapa cadangan, dan pemulihan akun, mis. dimanapun kriptografi asimetris digunakan, di mana kunci asimetris diperlukan. Semua ini dapat digunakan, tetapi pada saat yang sama sepasang kunci, dan mereka, tergantung pada kebutuhan, dapat dihasilkan sebanyak yang Anda suka. Jadi mereka semua akan bergantung pada kata sandi pengguna, dan ini sangat nyaman.

Dalam satu tong madu, itu bukan tanpa lalat di salep.

Dan fitur teknologi ini sangat baru. Ini menggunakan kurva eliptik, yang untuk operasi bilinear ( BLS12-381 ). Matematika itu sendiri telah ada selama beberapa waktu, tetapi kurva khusus ini, yang digunakan khususnya dalam implementasi kami, hanya digunakan dalam ZCash kecuali kami. Dengan demikian, perpustakaan yang menggunakan matematika baru ini dapat dihitung dengan jari satu tangan. Untuk membawa ini ke dalam keadaan produksi, Anda perlu menghabiskan sejumlah waktu dan upaya. Namun demikian, industri tidak tinggal diam dan semua kerugian ini bersifat sementara. Sebagai konsekuensi dari dua properti pertama, kecepatan operasi bilinear ini tidak terlalu konsisten dengan matematika modern, khususnya elips, yang kita semua gunakan sekarang, ketika kita menggunakan protokol TLS, ketika kita menggunakan beberapa situs. Ini adalah sekitar beberapa ratus operasi pada layanan pada satu inti. Sebenarnya, ini tidak menghentikan kami dan pada musim semi kami menerapkan protokol ini, merilisnya dalam produksi dan menerjemahkan semua catatan kami, melindungi mereka menggunakan protokol ini. Pada prinsipnya, kami puas dengan kinerja untuk tugas-tugas kami saat ini, jika perlu, kami akan meningkatkan simpul lain dengan layanan Pythia dan, pada prinsipnya, Anda sudah bisa bermain dengan semua ini.
PHE

Tetapi kami berpikir apakah kami bisa melakukan yang lebih baik lagi? Apakah mungkin untuk mencapai properti yang disediakan oleh Pythia dengan menggunakan matematika kemarin? Bukan besok, bukan hari ini, tapi bahkan kemarin, yang telah digunakan selama bertahun-tahun.

Dan secara harfiah pada bulan Juli tahun ini, para ilmuwan merilis sebuah protokol baru yang disebut Layanan Enkripsi Hardened Simple Password, atau singkatnya PHE.

Ini adalah Russell Lai , seorang ilmuwan dari Eropa.
Apa kelebihan layanan ini? Pertama, ia menggunakan kurva P-256 standar, yang digunakan di mana-mana, di semua browser, produk, di mana saja kurva default, yang telah ada selama bertahun-tahun. Kedua, benda ini bekerja sekitar 10 kali lebih cepat daripada Pythia dan menggunakan primitif standar. Agak sulit, tetapi Anda bisa menerapkannya dengan tangan Anda sendiri tanpa menggunakan perpustakaan yang tidak jelas. Anda dapat menggunakan OpenSSL , atau Bouncy Castle , apa saja.

Tapi itu bekerja sedikit berbeda. Sekali lagi ada backend, ada layanan PHE. Backend memiliki kunci publik, layanan ini memiliki kunci pribadi y . Tidak seperti Pythia, proses registrasi dan proses verifikasi kata sandi sedikit berbeda. Ketika seorang pengguna baru datang ke layanan dan ingin mendaftar, apa yang dilakukan backend? Sejak awal, dia bertanya ke layanan PHE, tolong beri saya beberapa data yang bisa saya gunakan untuk mendaftar, semacam catatan Pendaftaran. Layanan mengatakan OK dan menjawab backend dengan hal-hal berikut. Ini menghasilkan beberapa garam 32-byte acak ( sNonce ). Berdasarkan garam ini dan kunci privasinya y, ia menghasilkan dua angka, sebut saja mereka C0 dan C1 . Ini juga menghasilkan bukti ( Proof ) bahwa dua angka atau 2 poin ini dihasilkan secara tepat menggunakan kunci privasinya y , menggunakan protokol Schnorr (seperti pada protokol sebelumnya). Backend memeriksa Proof . Belum ada kata sandi di sini. Apa yang dilakukan backend? Untuk bagiannya, ia juga memiliki kunci pribadi klien pribadi x dan, setelah menerima kata sandi dari pengguna, ia melakukan hal yang sama seperti layanan, hanya menambahkan kata sandi di sana. Dibutuhkan cNonce acak (garam klien acak), kata sandi, dan sekali lagi menghasilkan 2 angka HC0 dan HC1 . Kenapa 2? Karena HC0 pertama digunakan untuk otentikasi, dan angka kedua HC1 mencampur beberapa angka acak M dikalikan dengan kunci pribadi x ( MC ). Angka M juga berukuran 32 byte dan nantinya dapat digunakan untuk mengenkripsi data pengguna (kami memiliki Layanan Enkripsi) ( catatan oleh penulis catatan: kunci enkripsi dalam hal ini adalah MC ). Nomor MC akan tersedia sebagai kunci hanya setelah pengguna memasukkan kata sandi yang benar. Ternyata pada tahap pendaftaran Anda dapat menghasilkan tidak hanya catatan otorisasi, tetapi juga kunci enkripsi, unik untuk setiap pengguna, yang dengannya Anda dapat mengenkripsi profilnya, beberapa data, dan sesuatu yang lain. Kemudian backend hanya menjumlahkan apa yang dikirim layanan dan apa yang dilakukannya - menambahkan poin-poin ini dan mendapatkan T0 dan T1 . Dalam kasus pertama, itu menambahkan dua ( C0 + HC0 ), dan dalam tiga yang kedua ( C1 + HC1 + MC ). Dan dia memasukkan garam-garam dasar 2 ( sNonce , cNonce ), dengan bantuan yang memperoleh angka-angka ini dan 2 angka ( T0 dan T1 ), yang ternyata merupakan hasil penjumlahan.

Dengan demikian, proses otentikasi pengguna terjadi dalam urutan terbalik. Pengguna memasukkan kata sandinya di backend. Backend menghitung HC0 dan dari apa yang ada dalam database, kurangi HC0 dari T0 dan mengirimkan C0 dihasilkan ke layanan bersama dengan garam server. Layanan, mengetahui garam server, menghitung titik yang sama dengan sendirinya dan terlihat, itu bertepatan dengan fakta bahwa ia mengirim backend atau tidak, jika cocok, maka kata sandi itu benar dan Anda dapat menjawabnya dengan nomor kedua C1 , yang akan dikurangkan bersama dengan HC1 dari nomor tersebut. T1 dan dapatkan kunci enkripsi. Dengan demikian, kata sandi untuk layanan PHE bahkan tidak hilang. Dia bahkan tidak meninggalkan backend. Itu adalah dalam bentuk beberapa poin dikalikan dengan kunci pribadi backend. Bahkan tidak ada seperti itu, tetapi pada saat yang sama, layanan jarak jauh dapat membuat kesimpulan yang ketat tentang apakah kata sandi ini benar atau tidak dan membuktikan, di samping itu, bahwa ia melakukan semua perhitungan menggunakan kunci pribadinya y .

Fitur apa yang dimiliki sistem ini?

Kata sandi, seperti yang saya katakan, tidak meninggalkan backend. Tetapi tidak seperti Pythia, Anda memerlukan kunci pribadi di backend. Yah, kita perlu dan perlu, simpan di suatu tempat. PHE memiliki semua fungsi dasar Pythia:
- Anda juga dapat mengeluarkan token pembaruan jika sesuatu terjadi pada Anda dengan kunci pribadi;
- Anda juga dapat melalui seluruh database, memperbarui dan semuanya akan seperti apa adanya;
- perlindungan pencarian;
- layanan tidak tahu apa-apa tentang kata sandi;
- (Pythia , , , , PHE );
- .

...
… . . passw0rd.io . password , 18- , , zero trust, .. . , , .. Let's encrypt . , . CLI , . 2 SDK , GO .Net, .

:
- .
- .
- .

, .
?
37. ?

.
Q: , ! . , Pythia update token, ? private key . update token? Atau tidak?
A: , update token- .
Q: . - update token-, Private key ?
A: , update token-, , - , , , update token. , .. .
Q: , , , .
A: .. .
Q: , , , - Pythia - , , , ?
A: .
Q: ?
A: , Pythia . Yaitu , .
Q: ( ) bcrypt ?
A: , , , .
Q: , . ? , …
A: password
Q: password ? Api! Umumnya.
A: 123456 , 12345, 123456.
Q: . Pythia , PHE .
A: , .
Q: . . ? production ?
A: . ! Pythia.
Q: Pythia, , ?
A: .
Q: , ?
A: .
Q: , , !
A: SDK, .
Q: , , , , .. - , ? ? ?
A: , , , .. PHE, , 5 2 , 2 5 . , . PHE ( , ), , 10 , .
Q: .. - , - ? ?
A: . rate limiting, , .
Q: .. , ?
A: .
Q: . , .. Pythia (), , ? ?
A: , , .
Q: , update ?
A: , Pythia , , - - , , , )
A: ? ! . , , PHE, , .
Kesimpulan
PHE ( ) + — ( , , ) ( ). PHE , .
:
, .
Scratch Virgil Security , , !
( )?
UPD : Scratch . . , . .