Hei, tumpukan penuh, mari kita latih keterampilannya. Saya menyarankan meremas gyrus, menurut saya, menarik untuk melakukan ini menggunakan paradigma yang berbeda dan tidak biasa. Sebagian besar pengembang memiliki keterampilan algoritma yang dikembangkan - tugas berubah menjadi batu bata yang perlu dihubungkan, untuk memikirkan urutan langkah yang mengarah pada kesimpulan yang diinginkan.
Di sini, seminggu yang lalu, Prolog disebutkan, saya ingin menjawab bahwa bahasa Prolog cocok untuk menyelesaikan masalah. Saya sudah menyentuh tentang topik ini, dan mengutip beberapa solusi dari tugas acak yang tersedia untuk saya dari situs dengan tugas untuk algoritma , saya ingin menunjukkan bahwa setiap solusi kompleks tersedia dalam bahasa deklaratif, dan itu dapat bekerja tidak lebih lambat (well, mungkin terasa tidak terlalu lambat).
Butuh waktu lama untuk mempresentasikan masalah berikutnya, dan solusi pertama telah diterima, saya mendemonstrasikan masalah dan mencari tahu seberapa lambatnya.
Prolognya menarik karena Anda dapat membuat program deduktif yang menunjukkan banyak solusi dan bahkan dapat membatasinya, tetapi tidak memberikan cara untuk beralih,
Algoritma akan dikembangkan pemecah juru bahasa
Jadi, tugasnya adalah ini :
- Menjebak air hujan ii
Diberikan matriks mxn dari bilangan bulat positif yang mewakili ketinggian setiap sel unit dalam peta ketinggian 2D, hitung volume air yang mampu ditangkap setelah hujan.
Catatan:
Baik m dan n kurang dari 110. Tinggi setiap sel satuan lebih besar dari 0 dan kurang dari 20.000.
Contoh:
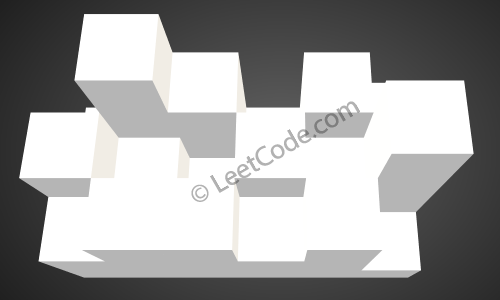
Diberikan peta tinggi 3x6 berikut:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]
Kembali 4.
Setelah upaya yang panjang untuk merumuskan solusi, saya sampai pada kata-kata ini:
Penting untuk menuangkan air maksimum ke setiap sel, yang tidak akan keluar darinya . Saya sarankan untuk menuangkan sejumlah air ke setiap sel, tetapi agar kurang dari nilai maksimum yang dimungkinkan.
Ternyata seperti ini:
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!.
predikat ini mengambil daftar input (matriks), dan mengubahnya menjadi solusi, menjadi matriks di mana ada nilai lain yang akan menjadi jawaban yang valid. Kemudian predikat lain mengambil dua daftar elemen ini dengan elemen dan menemukan jumlah total.
repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X).
predikat ini akan mengambil salah satu solusi, dan memeriksa apakah sudah "normal" diisi, jika memenuhi kondisi masalah, maka ini solusinya.
Ini adalah metode "hasilkan dan verifikasi", kami mengatakan bahwa nilainya dalam set dan kami merevisi semua elemen dari set ini, memeriksa semacam kondisi keluar.
Jadi, maka saya akan mendapatkan solusi baru dengan predikat put (Vals, X0, X1), di sini pertama-tama adalah daftar semua ketinggian yang mungkin ada dalam matriks ini, dari mana kita akan memilih ketinggian yang mungkin untuk setiap sel. Menurut analisis tes input, ditemukan bahwa dalam masalah ini adalah mungkin untuk mengisi seluruh sel, jika begitu banyak air dapat dimasukkan di sekitarnya sehingga dituangkan "di atas kepala".
Secara total, predikat ini terlihat lebih rumit, perlu untuk memproses tiga kali lipat dari garis yang membentuk satu 3x3 kuadrat (ya, tidak ada array di Prolog, tetapi sepertinya deskripsi data input, jadi kami menggunakannya dalam pemrograman deklaratif, Anda mungkin tidak tahu tentang indeks elemen dalam array) , hanya ada daftar dengan kepala dan ekornya, jadi jelaskan template yang cocok dengan spesifikasi input).
puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St).
Ini adalah bagaimana hasilnya mengekspresikan bypass dari matriks, dari mana Anda dapat mengambil tiga baris pertama (dan selanjutnya), dari mana, Anda juga dapat memilih, dari kiri ke kanan, tiga kali lipat elemen, dan di antara delapan tetangga akan ada satu sel [Itaya] [Utaya] lanskap. Dengan bantuan sel_biger (R2, V, R21) makna baru dari sel ini dibuat.
Nilai ini dapat diatur ke sel saat ini, itu bisa menjadi salah satu ketinggian yang mungkin, dan bahkan daftar diurutkan dalam urutan menurun, sehingga yang pertama akan menjadi ketinggian tertinggi yang tersedia sama sekali, dan kemudian mengikutinya:
sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X).
Itu adalah deskripsi dari "pembuat keputusan," dan kemudian Anda perlu memastikan bahwa matriks yang diperoleh, dari ketinggian yang diisi secara sewenang-wenang di setiap titik, mirip dengan jawaban yang kami butuhkan.
Dan diharuskan untuk menemukan keadaan sedemikian rupa sehingga air mengendap di dalam lubang, saya akan mencoba mengatakannya seperti ini:
dari sembilan nilai bujur sangkar adalah tiga kali tiga, di tengah harus selalu ada ketinggian sehingga tidak bertentangan dengan peta input, sehingga perubahan keseimbangan yang semula di dalam sel-sel ini tidak diperoleh, jika ada tinggi, maka seharusnya tidak ada sel di atasnya, bahkan jika semuanya akan membanjiri air, maka di sini kita dapat mengatakan bahwa sel yang tinggi harus tetap dengan sendirinya atau diganti dengan nilai yang lebih tinggi, tetapi sedemikian rupa sehingga sama dengan semua tetangga, mis. sel-sel ke kiri, ke kanan dan dari atas ke bawah dari arus harus melebihi atau sama, jika ada lebih banyak air dalam sel, maka hanya jika telah naik sekitar ...
Dan dua predikat akhir, yang mengambil matriks input, memulai pencarian untuk hasil yang cocok, kurangi jumlah elemen di antara mereka sendiri, dan temukan jumlah akhir yang diperlukan dalam masalah:
diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. %% , sums(X,S):-reptest(X,X1),diffall(X,X1,S).
Saya akan menunjukkan tes yang disediakan situs .
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). % balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). % , 33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). % , % equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-reptest(X,X1),diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([],0),true). :-assert_are_equal(sums([[1]],0),true). :-assert_are_equal(sums([[2,3]],0),true). :-assert_are_equal(sums([[3],[2]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). %:-assert_are_equal(sums([[9,9,9,9,9,9,8,9,9,9,9],[9,0,0,0,0,0,1,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,9,9,9,9,9,9,9,9,9,9]],215),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). %:-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true).
Saya harus mengomentari tes. tidak semua melewati.
Tugasnya adalah bagaimana mempercepatnya?
Beberapa solusi tidak dapat ditemukan, karena pencarian solusi yang panjang, mereka dihasilkan terlalu lambat dalam urutan ini, di sini kompleksitasnya mungkin n !, semua nilai yang mungkin untuk setiap sel array diurutkan.
Lebih mudah untuk mengekspresikan tugas ini dalam sistem pemrograman dalam batasan, hanya di Prolog disebut seperti ini: CLP (FD): Constraint Logic Programming over Finite Domains.
clp (fd) adalah perpustakaan yang termasuk dalam distribusi standar SWI-Prolog. Ini memecahkan masalah yang melibatkan set variabel, di mana hubungan antara variabel perlu dipenuhi.
>>
Saya merumuskan masalah seperti ini:
Kita memerlukan daftar seperti itu, setiap elemen dari himpunan nilai lebih dari atau sama dengan nilai maksimumnya di seluruh peta, dengan mempertimbangkan batasan bahwa elemen-elemen harus ditempatkan dengan jelas sesuai dengan cairan tumpahan yang sesuai.
Inilah yang saya lakukan dari daftar input, daftar baru yang unsur-unsurnya menjadi tidak dikenal dalam rentang tertentu (dari nilai R2 elemen saat ini ke nilai maksimum V)
Pada input, daftar daftar, pada output, daftar baru dengan distribusi nilai maksimum,
yang memenuhi batasan "keseimbangan cairan" botak:
checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
Ini adalah generator dan cek pada saat yang sama, diindikasikan bahwa elemen-elemen berada dalam set seperti itu, dan kemudian secara bertahap memaksakan cek, set ini dipersempit. Selanjutnya, sesuatu tetap ada, dan itu bisa "ditandai", yaitu menetapkan nilai integer yang akan memenuhi jumlah semua kendala. Pelabelan panggilan ([bawah], FX2) memaksa untuk mengisi (kontak) variabel tidak diketahui dengan nilai spesifik, dan mungkin ada beberapa opsi seperti itu, tetapi kami akan selalu mengambil yang pertama, karena dikatakan bahwa semua variabel bergerak ke bawah dalam pencarian, dari batas atas mereka, ini adalah opsi pencarian [turun].
Dan di sana Anda dapat melihat pengaturan rumit seperti:16.2.1. strategi pemilihan variabel
Strategi pemilihan variabel memungkinkan Anda menentukan variabel Vars mana yang dilabeli berikutnya dan merupakan salah satu dari:
paling kiri - Label variabel dalam urutan mereka terjadi di Vars. Ini standarnya.
ff Pertama gagal. Beri label variabel paling kiri dengan domain terkecil berikutnya, untuk mendeteksi ketidaklayakan lebih awal. Ini sering merupakan strategi yang baik ketika ada domain kecil untuk variabel berikutnya ketika variabel pertama dipilih.
ffc Dari variabel dengan domain terkecil, yang paling kiri yang berpartisipasi dalam sebagian besar kendala diberi label berikutnya. Menerapkan kendala harus menghapus subtree, jadi ini bisa menjadi strategi yang baik.
min Label variabel paling kiri yang batas bawahnya adalah terendah berikutnya. perhatikan bahwa ini adalah min / 0, berbeda dari min / 1, yang menentukan solusi solusi dan dibahas pada bagian sebelumnya di atas. Ini adalah taktik yang baik jika Anda mencoba untuk meminimalkan beberapa nilai global yang cenderung lebih rendah jika berbagai variabel (misalnya solusi biaya minimum).
Maks label variabel paling kiri yang batas atasnya adalah tertinggi berikutnya. Ini juga berbeda dari maks / 1. Dan saran untuk min berlaku untuk maks ketika mencoba memaksimalkan nilai global.
16.2.2. urutan nilai
Urutan nilai adalah salah satu dari:
up Coba elemen dari domain variabel yang dipilih dalam urutan menaik. Ini standarnya.
bawah Coba elemen domain dalam urutan menurun.
Jelas, jika Anda memiliki distribusi asimetris, seperti yang kami tunjukkan dalam cara memberi label secara efisien di atas, coba elemen dalam urutan pertama yang paling umum.
16.2.3. strategi percabangan
Strategi percabangan adalah salah satu dari:
langkah Untuk setiap variabel X, sebuah pilihan dibuat antara X = V dan X # \ = V, di mana V ditentukan oleh opsi pengurutan nilai. Ini standarnya.
enum Untuk setiap variabel X, sebuah pilihan dibuat antara X = V_1, X = V_2 dll., untuk semua nilai V_i dari domain X. Urutan ditentukan oleh opsi pemesanan nilai.
membagi dua Untuk setiap variabel X, pilihan dibuat antara X # = <M dan X #> M, di mana M adalah titik tengah dari domain X. Pilih opsi ini jika banyak variabel pilihan di antara berbagai bilangan bulat, nilai, daripada satu di antara seperangkat nilai yang disebutkan (misalnya persentase, vs a = 0, b = 1, c = 2)
Sekarang sebenarnya apa yang “seimbang” adalah ketika air yang dituangkan tidak meluap dari sel ke sel. Ini adalah korespondensi dari pemesanan awal elemen. Orang mungkin berpikir bahwa mengisi sel akan mempertahankan bentuk lanskap asli, yang berarti jika ada dinding, maka dapat ditutupi dengan air di atasnya, sehingga menjadi sama dengan semua tetangganya, atau jika bukan dinding yang ditutupi dengan air ...
Pertimbangkan situasi seimbang:
-Jika sel dibanjiri, maka di sebelahnya sama atau bahkan lebih tinggi (tiba-tiba itu dinding).
-Jika sel itu sama dengan sel tetangga, maka itu harus sama dengan sel tetangga baru.
-Dan kasus ekstrim, sel tidak mengubah artinya, dan masih seperti apa tetangga yang dimilikinya:
Ini adalah bagaimana Anda dapat mentransfer sikap Anda terhadap tugas ke dalam program. Tidak perlu bagi saya untuk memikirkan algoritma keputusan, penting untuk memberikan deskripsi hasil yang benar, untuk mengatur dengan benar semua kendala awal (set nilai). Pendekatan ini hanya dapat "dicampur" dengan pencarian biasa dengan pengembalian dan rekursi yang melekat pada Prolog. Ini adalah cara untuk merumuskan lebih banyak program deklaratif daripada menggunakan metode Prolog klasik .
Saya akan memberikan solusi yang diperoleh, dengan serangkaian tes:
:- use_module(library(clpfd)). checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
Dan lebih banyak tes :-assert_are_equal(sums([[13,16,15,18,15,15],[14,1,8,9,7,9],[19,5,4,2,5,10],[13,1,7,9,10,3],[17,7,5,10,6,1],[15,9,8,2,8,3]],36),true). :-assert_are_equal(sums([[18,13,13,17,12,11],[17,2,6,10,5,10],[11,10,2,8,8,2],[12,6,10,8,8,7],[18,4,7,6,7,4],[20,5,9,2,3,10]],18),true). :-assert_are_equal(sums([[14,20,11,19,19,16],[11,10,7,4,9,6],[17,2,2,6,10,9],[15,9,2,1,4,1],[15,5,5,5,8,7],[14,2,8,6,10,7]],11),true). :-assert_are_equal(sums([[19383,10886,12777,16915,17793,18335,15386,10492,16649,11421],[12362,27,8690,59,7763,3926,540,3426,9172,5736],[15211,5368,2567,6429,5782,1530,2862,5123,4067,3135],[13929,9802,4022,3058,3069,8167,1393,8456,5011,8042],[16229,7373,4421,4919,3784,8537,5198,4324,8315,4370],[16413,3526,6091,8980,9956,1873,6862,9170,6996,7281],[12305,925,7084,6327,336,6505,846,1729,1313,5857],[16124,3895,9582,545,8814,3367,5434,364,4043,3750],[11087,6808,7276,7178,5788,3584,5403,2651,2754,2399],[19932,5060,9676,3368,7739,12,6226,8586,8094,7539]],79058),true). :-assert_are_equal(sums([[10795,10570,11434,10378,17467,16601,10097,12902,13317,10492],[16652,756,7301,280,4286,9441,3865,9689,8444,6619],[18440,4729,8031,8117,8097,5771,4481,675,709,8927],[14567,7856,9497,2353,4586,6965,5306,4683,6219,8624],[11528,2871,5732,8829,9503,19,8270,3368,9708,6715],[16340,8149,7796,723,2618,2245,2846,3451,2921,3555],[12379,7488,7764,8228,9841,2350,5193,1500,7034,7764],[10124,4914,6987,5856,3743,6491,2227,8365,9859,1936],[11432,2551,6437,9228,3275,5407,1474,6121,8858,4395],[16029,1237,8235,3793,5818,4428,6143,1011,5928,9529]],68900),true). :-assert_are_equal(sums([[18776,12404,14443,15763,14613,14538,18606,16840,12904,14818],[15128,688,7369,7917,9917,6996,3324,7743,9470,2183],[18490,5499,9772,6725,5644,5590,7505,8139,2954,9786],[17669,8082,8542,8464,197,9507,9355,8804,6348,8611],[13622,7828,9299,7343,5746,5568,4340,5422,3311,3810],[17605,1801,5661,3730,4878,1305,9320,8736,9444,8626],[18522,3465,6708,3416,8282,3258,2924,7637,2062,5624],[12600,2036,3452,1899,9379,5550,7468,71,973,7131],[13881,4930,8933,5894,8660,163,7199,7981,8899,2996],[12959,3773,2813,9668,7190,1095,2926,6466,5084,1340]],61413),true). :-assert_are_equal(sums([[12090,17684,13376,15542,15936,19107,17445,19756,19179,18418],[16887,9412,3348,2172,1659,2009,2336,5210,6342,7587],[18206,9301,7713,7372,5321,1255,4819,4599,7721,9904],[15939,9811,3940,5667,1705,6228,1127,9150,5984,6658],[13920,9224,2422,7269,1396,4081,5630,84,9292,1972],[17672,3850,7625,5385,1222,9299,6640,6042,3898,713],[12298,6190,524,2590,8209,8581,8819,9336,7732,1155],[15994,8004,379,4769,5273,1776,8850,7255,1860,8142],[15579,5884,1993,3205,7621,9567,2504,613,1961,2754],[11326,4259,8944,8202,3202,3506,6784,2021,2842,868]],89383),true). :-assert_are_equal(sums([[19528,15189,18872,19908,19958,10498,18036,18808,17753,16248],[13303,3333,2133,1648,2890,9754,7567,1746,368,9529],[14500,8046,3788,9797,6249,6990,3303,3033,5363,2497],[10253,4892,7686,9125,1152,3996,5975,9188,9157,3729],[15436,2460,3414,3921,460,6304,28,8027,8050,6748],[17556,8902,4794,7697,8699,1043,1039,2002,428,6403],[14500,681,7647,8538,6159,5151,2535,2134,4339,1692],[12215,6127,504,5629,49,964,8285,6429,5343,6335],[13177,2900,5238,7971,6949,289,5367,7988,2292,5795],[10743,3144,2829,8390,1682,5340,3541,569,3826,4232]],100439),true).
Ini adalah tes dari situs, hanya 30 buah pertama. Hasilnya sangat bagus, masalahnya terpecahkan, dan bahkan cepat, setiap saat hingga satu detik.
Anda dapat memeriksa ...
Sebagai kesimpulan
Pemrograman deklaratif melibatkan formalisasi rinci dari tugas, dan pemecah akan mencari solusi paling efektif yang akan memenuhi kondisi.
Sedikit lebih dalam ke topik, Anda dapat membuka minizinc , bahasa pemrograman di mana paradigma ini tertanam. Mereka merumuskan banyak makna, menunjukkan batasan, dan voila, jawabannya. Mereka memecahkan Sudoku , tugas pewarnaan peta, pekerjaan penjadwalan , masalah sumber daya, Penjadwalan. Saya sarankan untuk melatih ...