Matematika di Gamedev sederhana. Triangulasi dan Triangle.Net di Unity

Halo semuanya! Nama saya Grisha dan saya adalah pendiri CGDevs. Matematika adalah alat yang sangat keren ketika mengembangkan game. Tetapi jika kita mengatakan sulit untuk mengelola tanpa memahami vektor dan matriks , maka algoritma triangulasi bukanlah hal yang diperlukan, tetapi dengan mereka sejumlah besar masalah menarik diselesaikan. Hari ini saya ingin berbicara tentang alat yang agak penting dalam geometri komputasi, seperti triangulasi dan aplikasinya dalam industri game. Selain itu, saya menulis port dan beberapa pembungkus untuk library Triangle.Net yang sangat baik untuk Unity. Jika tertarik - selamat datang di kucing. Tautan ke github terlampir.

Apa itu triangulasi?

Dalam kasus umum, triangulasi adalah partisi dari objek geometris menjadi segitiga. Konsep ini sendiri cukup sederhana. Contoh dasar triangulasi dalam kasus mesin game adalah mesh. Sebenarnya, sebuah mesh dapat terdiri tidak hanya dari segitiga, tetapi dalam mesin game karena berbagai alasan itu adalah mesh yang terdiri dari segitiga yang diambil.



Triangulasi berbeda, tetapi salah satu jenis triangulasi yang paling populer adalah triangulasi Delaunay. Jenis triangulasi ini dibedakan berdasarkan sifat yang dalam lingkaran dibatasi di sekitar setiap segitiga, hanya simpul-simpul dari segitiga ini yang terletak.

Mengapa mereka dibutuhkan?

Secara umum, di luar industri game, sejumlah besar tugas diselesaikan dengan bantuan triangulasi. Di game dev, tugas pertama yang muncul di benak adalah jala navigasi. Navmesh adalah struktur data yang menentukan seberapa banyak ruang yang bisa dilalui pemain. Ini menghindari tugas komputasi yang kompleks seperti menentukan tabrakan dengan bagian dari lingkungan.

Masalah menarik kedua yang dapat dipecahkan dengan menggunakan triangulasi Delaunay dalam pengembangan game adalah generasi medan dan objek yang direpresentasikan sebagai sekumpulan poin. Keuntungan utama dari triangulasi Delaunay dalam hal ini adalah bahwa, berdasarkan sifat-sifatnya, ini memungkinkan Anda untuk menghindari segitiga yang sangat tajam yang akan mengganggu dan membuat artefak pada saluran pembuangan.



Selain itu, dengan menggunakan triangulasi dan algoritma Delaunay terbatas seperti algoritma kedua Chew dan algoritma Ruppert, Anda dapat menghasilkan jerat yang lebih baik untuk tirrains dan menghasilkan jerat yang baik untuk aplikasi lain - metode elemen hingga.

Metode elemen hingga itu sendiri adalah salah satu metode untuk menyelesaikan masalah fisika terapan. Dalam gamedev, ini memungkinkan Anda untuk menyelesaikan banyak masalah yang terkait dengan simulasi deformasi, simulasi fluida dan lainnya yang digunakan untuk khusus. efek. Biasanya untuk merekam efek dalam animasi, karena untuk real time metode ini memiliki kompleksitas komputasi yang terlalu tinggi. Detail penting ketika menggunakan metode ini adalah bahwa kesalahan metode tergantung pada sudut segitiga dalam kotak. Jika ada sudut yang sangat tajam di grid, metode ini memberikan kesalahan besar, untuk alasan ini diperlukan algoritma yang tercantum di atas.



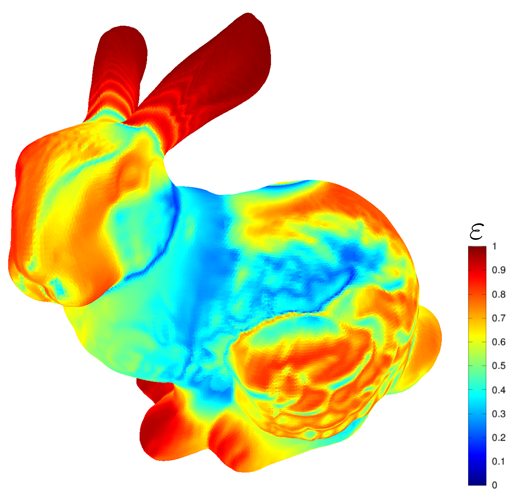
Dan tentu saja, secara umum, generasi mesh prosedural. Sebagai contoh, proyek github menunjukkan adegan dengan kemampuan menggambar jerat. Beberapa teka-teki fisik menggunakan aplikasi ini sebagai mekanik dasar. Tetapi di samping itu, algoritma triangulasi memungkinkan penggunaan generasi prosedural untuk menyelesaikan masalah seperti destruksibilitas prosedural dan sebagainya.

Selain triangulasi gamedev digunakan dalam jaringan, visi komputer, berbagai algoritma analitik, serta dalam masalah apa geometri komputasi, seperti menggabungkan dan menghilangkan poligon satu sama lain (yang sering berguna dalam masalah yang timbul dalam pengembangan game)

Kliping Telinga dengan Lubang

Mungkin salah satu algoritma triangulasi paling sederhana. Itu tidak memberikan grid terbaik dan memiliki kompleksitas komputasi terbesar O (n ^ 2) dalam kasus terburuk.

Anda dapat membaca lebih lanjut tentang itu di artikel ini.

Algoritma Bowyer - Watson

Algoritma yang menghasilkan triangulasi Delaunay atas satu set poin. Secara umum, seperti kebanyakan algoritma Delaunay, jika diterapkan dengan benar, kompleksitas algoritmiknya adalah O (n log n), di mana n adalah jumlah simpul. Tetapi dalam beberapa kasus mungkin butuh O (n ^ 2).

Kerugian terkait Kliping Telinga adalah bahwa algoritma ini membangun triangulasi cembung dan dalam implementasi dasarnya tidak melibatkan lubang di kisi yang dihasilkan.

Pemrosesan pemurnian Delaunay

Algoritma kedua Chew dan algoritma Ruppert adalah algoritma yang memungkinkan Anda untuk memasukkan batasan dalam triangulasi Delaunay dan mengatur sudut minimum segitiga dalam kisi. Detail penting dari algoritma adalah bahwa mereka dapat masuk ke loop tak terbatas dan dijamin untuk memberikan hasil pada sudut antara sekitar 20,7 derajat dan 29 derajat. Kemampuan untuk mengatur sudut minimum adalah penting dalam menyelesaikan masalah yang dijelaskan di atas.

Algoritma kedua Chew diimplementasikan dalam paket gratis www.cs.cmu.edu/~quake/triangle.html dan port-nya di .Net archive.codeplex.com/?p=triangle

Triangle.Net untuk Persatuan

Nah, karena dengan bantuan triangulasi Anda dapat menyelesaikan begitu banyak tugas keren, di hari libur saya ingin menerapkan pembungkus saya untuk Unity, sehingga saya selalu memiliki alat yang berguna. Dalam implementasi ini, algoritma triangulasi bekerja rata-rata untuk O (n), dan dalam kasus terburuk untuk O (n * log n), di mana n adalah jumlah simpul. Sebagai contoh, ketika pengujian untuk simpul 1kk tersebar secara acak di seluruh kotak, unit-unit dalam editor pada Intel Core i7-8700 membangun sebuah kotak dalam rata-rata 7,56 detik.

Perbedaan utama dari perpustakaan asli dengan adanya metode ekstensi yang dirancang untuk Unity, serta penggantian ganda dengan float di seluruh perpustakaan (+ beberapa operator khusus untuk casting) Double di unit, tidak masuk akal. Jika kita mempertimbangkan simulasi fisik, maka saya akan menggunakan aplikasi terpisah di perpustakaan plus, dan hasil perhitungan sudah memberi Unity murni untuk visualisasi. Dan juga mengganti nama tipe Mesh ke TriangleNetMesh agar tidak merobohkan relatif ke Mesh dari Unity. Ya, mereka sudah berada di ruang nama yang berbeda, tetapi bagaimanapun, saya pikir para pendatang baru akan sedikit dirobohkan oleh fakta bahwa dengan bantuan dari satu Mesh kita mendapatkan yang lain.

Inti dari pustaka adalah Anda harus terlebih dahulu menentukan apa yang disebut poligon. Kemudian, berdasarkan itu, sudah menghasilkan mesh. Agar ini bekerja dengan struktur data unit, beberapa metode ekstensi telah diperkenalkan.



Untuk contoh demonstrasi dan penggunaan, adegan demo khusus dibuat dengan kemampuan untuk menggambar jerat. Anda bisa berkenalan dengannya dan port perpustakaan di proyek github.

Terima kasih atas perhatian anda! Saya berharap bahwa port dan artikel akan bermanfaat bagi seseorang dan akan menjadi sedikit lebih jelas mengapa triangulasi dan pengetahuan matematika secara keseluruhan diperlukan. Saya akan mencoba untuk terus mengungkapkan aplikasi dan metode untuk menyelesaikan berbagai masalah matematika dalam pengembangan game. Dalam komputasi geometri itu sendiri masih ada banyak hal yang menarik, tetapi selain itu masih ada banyak bagian lain yang menarik dari matematika yang lebih tinggi.