Pertimbangkan seri waktu perkiraan. Mari kita coba memprediksi grafik kutipan, atau hal lain yang berguna.
Mari kita ambil sebagai dasar peramalan yang disajikan dalam artikel
Model Perkiraan Rangkaian Waktu untuk Contoh Kesamaan Maksimum: penjelasan dan contoh (artikel ini bukan milik saya). Poin singkatnya adalah bahwa segmen grafik yang paling mirip di sebelah kiri perkiraan di antara riwayat masa lalu dicari, dan kemudian nilai di sebelah kanan grafik kemudian diambil dari yang terbaik yang lama ini dan digunakan sebagai perkiraan.
Saya akan melangkah lebih jauh. Saat menghitung perkiraan, saya tidak akan mengambil satu kasus pun yang terbaik dalam korelasi, tetapi satu pak yang terbaik. Dan perkiraan akan menjadi hasil rata-rata untuk paket ini. Ini akan memungkinkan untuk memahami bahwa nilai yang ditemukan adalah keteraturan, dan bukan kebetulan kebetulan dengan perkiraan yang diinginkan, atau penyimpangan acak jika ramalan menyimpang dari yang sebenarnya.
Menggunakan opsi tunggal terbaik seperti dalam artikel itu tidak benar, serta menentukan distribusi probabilitas dengan satu nilai dari distribusi ini. Jika Anda menghasilkan grafik yang sangat besar dari data acak dan memulai pencarian pada mereka, maka pasti akan ada segmen yang berkorelasi di dalamnya, dan bahkan mungkin dengan koefisien 0,9999, tetapi sama sekali tidak perlu bahwa segmen yang sama akan terus mengikuti segmen ini - masih semuanya acak. Dan Anda hanya perlu mengambil paket segmen tersebut dan menghitung bahwa varians dari data selanjutnya lebih rendah dari varians yang terbentuk dari sampel acak dari data ini. Dan jika dispersi paket lebih rendah - maka ini adalah perkiraan. Meskipun ini juga bukan representasi akurat dari kemungkinan kesalahan, ini sudah cukup untuk saat ini.
Yaitu
peramalan bukanlah prinsip pengambilan sampel dan korelasi dari segmen yang dibandingkan yang kami gunakan, hal utama adalah bahwa sebagai hasil dari penerapan sampel ini, varians dari nilai yang diinginkan akan lebih kecil daripada sebagai hasil dari pengambilan sampel acak.
Juga, varian dari paket ini akan memungkinkan untuk mengevaluasi mana yang lebih baik untuk menggunakan opsi pemilihan dari kasus-kasus sebelumnya. Bagaimanapun, adalah mungkin untuk memilih tidak selalu satu segmen data yang berkorelasi, dan tidak selalu menggunakan korelasi Pearson. Dan pilihan seperti itu dapat dibuat untuk setiap titik yang diperkirakan secara terpisah. Untuk jenis sampel varians lebih sedikit, opsi itu lebih baik untuk titik saat ini.
Paket ukuran apa yang seharusnya? Ini bertumpu pada masalah interval kepercayaan. Agar tidak memuat terlalu banyak, ada disebutkan bahwa lebih baik mengambil setidaknya 30 contoh untuk menentukan nilai rata-rata. Jika ada kelebihan data uji, saya akan mengambil setidaknya 100.
Rasio dari standar deviasi sampel sesuai dengan algoritma dan yang acak dapat disebut koefisien teoritis keberhasilan algoritma peramalan untuk titik saat ini untuk tujuan perbandingan dengan algoritma pengambilan sampel lainnya, atau untuk menentukan kegunaan perkiraan ini secara umum, sedangkan nilai aktual belum tersedia.
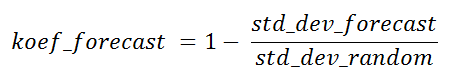
Koefisien ini dalam beberapa kasus dapat mengambil nilai negatif. Poin-poin di mana hal ini terjadi adalah sedikit menarik, seperti poin-poin dengan koefisien nol. Dalam hal prediktabilitas 100%, itu akan sama dengan satu.
Mari kita beralih ke contoh praktis, lagi dari artikel itu. Setelah memperbaiki kesalahan kecil di sana, kami mendapatkan hasil berikut, konsisten dengan artikel itu dan algoritma itu:
perhitungan perkiraan pada saat 9/1/2012 23:00 posisi 52631
nilai total diperiksa untuk kemiripan 2184
korelasi terbaik posisi 0,958174 52295
koefisien transfer alpha (1/2) 1.03117 -11.1992
perkiraan kesalahan dari fakta mape 5.210%mape - istilah dari artikel asli Mean Persentase Absolute Error, dihitung dengan rumus
Abs (Prakiraan - Fakta) / FaktaDan sekarang mari kita membuat pilihan bukan satu kesamaan terbaik, tetapi paket yang terbaik dan segalanya untuk memprediksi satu saat dalam waktu dan melihat apa yang terjadi:
0 koreksi 0,958174 pos 52295 mape 5,210%
1 kor 0,953571 pos 52151 mape 6,566%
2 kor 0,953532 pos 45599 mape 11,642%
3 kor 0,951462 pos 45743 mape 7,033%
4 kor 0,950921 pos 45575 cetakan 3,300%
5 kor 0,950789 pos 38687 mape 3,538%
Nilai korelasi di sini berubah dari nilai ke nilai yang dapat diabaikan. Pada saat yang sama, nilai hasil perkiraan bervariasi dari 3% hingga 11%. Yaitu bahwa 5% awal tidak lebih dari kebetulan, bisa jadi 11% dan 3%.
Di bawah kondisi kesamaan yang ditentukan dalam artikel itu, nilai 2184 dapat dibandingkan secara total. Dari jumlah tersebut, saya mengambil paket yang terbaik dalam 1500 buah, diurutkan dalam urutan penurunan korelasi, dan ditampilkan dalam grafik. Korelasi dalam paket ini dari 0,958 terbaik turun menjadi 0,715 dari kiri ke kanan. Tetapi fluktuasi hasil praktis tidak berubah:

Dapat dilihat bahwa ketergantungan hasil pada korelasi sangat rendah, tetapi tampaknya tetap ada. Secara umum, kami mengambil paket dari 100 nilai teratas dan menghitung perkiraan, seperti yang saya sebutkan, dengan rata-rata untuk paket ini. Hasilnya adalah sebagai berikut:
mape 5,824%, stddev mape 7,035% . Tapi 5,8% ini bukan lagi kebetulan, tetapi rata-rata distribusi - perkiraan yang paling mungkin. Deviasi standar mape lebih besar daripada mape itu sendiri, tetapi ini karena mape memiliki distribusi non-simetris.
Saya juga menghitung perkiraan yang sama tetapi menggunakan sampel acak bersyarat, lebih tepatnya, hanya dirata-rata dari semua opsi yang mungkin, hasil
mape adalah 8,246% . Dengan pengambilan sampel acak, kesalahannya sedikit lebih besar, tetapi nilai ini masih dalam kisaran sebaran yang dihitung dari sampel terbaik. Untuk titik yang dihitung, koefisien peramalan teoritis yang ditunjukkan oleh saya mendekati nol, lebih tepatnya
koef_forecast = -0.041 . Saya tidak menghitungnya dari stddev mape (ini termasuk perkiraan sebenarnya), tetapi dari nilai absolut dari perkiraan tersebut, jika Anda melihat program maka angka awal untuk itu diberikan di sana.
Tapi ini kalau menyangkut cap waktu, yang disebutkan dalam artikel asli. Tetapi jika kita mengatakan “9/4/2012 23:00” (bulan / hari / tahun), maka koefisien efisiensi
teorinya adalah
koef_forecast = 0,21 , dan
mape = 3,126%, mape_rand = 7,147% . Yaitu koef_forecast menunjukkan sebelumnya bahwa titik saat ini akan dihitung lebih akurat daripada yang sebelumnya. Inti dari kegunaan koefisien ini adalah bahwa Anda setidaknya dapat mengevaluasi hasilnya bahkan sebelum mendapatkan data aktual, karena data aktual tidak berpartisipasi di dalamnya. Semakin tinggi, semakin baik. Saya sudah menyebutkan bahwa titik yang diprediksi mutlak akan memiliki koefisien satu.
Anda sendiri dapat melihat bagaimana semua angka ini berubah dalam program demo saya di Qt C ++, di sana Anda dapat memilih tanggal dan ukuran paket:
sumber di githubNilai terbaik dipilih berdasarkan algoritma berikut:
inline void OrdPack::add_value(double koef, int i_pos) { if (std::isfinite(koef)==false) return; if (koef <= 0.0) return; if (mmap_ord.size() < ma_count_for_pack) { if (mmap_ord.size()==0) mi_koef = koef; mi_koef = std::min(mi_koef, koef); mmap_ord.insert({-koef,i_pos}); } else if (koef > mi_koef) { mmap_ord.insert({-koef,i_pos}); while (mmap_ord.size() > ma_count_for_pack) mmap_ord.erase(--mmap_ord.end()); mi_koef = -(--mmap_ord.end())->first; } }
Tidak ada gunanya memposting seluruh sumber di sini, tidak rumit di sana, dan dengan komentar. Dasar dalam prosedur MainWindow :: to_do_test () dalam file
mainwindow.cpp .
Untuk saat ini, saya akan terus mencoba memprediksi sesuatu di bagian selanjutnya.
PS. Silakan tinggalkan komentar Anda tentang apakah semuanya jelas tentang apa yang hilang. Saya sudah menyusun rencana perkiraan untuk apa yang akan ditulis selanjutnya, tetapi dengan komentar Anda, saya akan melakukannya dengan lebih baik.