Teori kebahagiaan. Statistik sebagai cara ilmiah untuk tidak tahu apa-apa

Saya terus berkenalan dengan para pembaca Habr dengan bab-bab dari bukunya "Theory of Happiness" dengan subtitle "Yayasan Matematika dari Hukum Makna." Ini belum diterbitkan buku sains populer, sangat informal menceritakan tentang bagaimana matematika memungkinkan Anda untuk melihat dunia dan kehidupan orang-orang dengan tingkat kesadaran yang baru. Ini untuk mereka yang tertarik pada sains dan bagi mereka yang tertarik pada kehidupan. Dan karena kehidupan kita kompleks dan, pada umumnya, tidak dapat diprediksi, penekanan dalam buku ini terutama pada teori probabilitas dan statistik matematika. Di sini teorema tidak terbukti dan dasar-dasar sains tidak diberikan, ini sama sekali bukan buku teks, tetapi apa yang disebut ilmu rekreasi. Tetapi justru pendekatan yang hampir menyenangkan yang memungkinkan kita untuk mengembangkan intuisi, mencerahkan kuliah untuk siswa dengan contoh-contoh nyata dan, akhirnya, menjelaskan kepada non-matematikawan dan anak-anak kita apa yang begitu menarik yang kita temukan dalam ilmu kering kita.


Bab ini membahas statistik, cuaca, dan bahkan filsafat. Jangan khawatir, hanya sedikit. Tidak ada lagi yang bisa digunakan untuk tabletalk di masyarakat yang layak.

Angka-angka itu menipu, terutama ketika saya melakukannya sendiri; pada kesempatan ini, pernyataan yang dikaitkan dengan Disraeli benar: "Ada tiga jenis kebohongan: kebohongan, kebohongan yang mencolok, dan statistik."
Mark Twain

Betapa sering di musim panas kita berencana untuk pergi keluar, berjalan-jalan di taman atau piknik, dan kemudian hujan merusak rencana kita, memenjarakan kita di rumah! Dan yah, jika ini terjadi sekali atau dua kali musim, kadang-kadang tampaknya cuaca mengikuti akhir pekan, sampai Sabtu atau Minggu lagi dan lagi!

Sebuah artikel yang relatif baru diterbitkan oleh para peneliti Australia: "Siklus mingguan suhu puncak dan intensitas pulau termal perkotaan." Dia dijemput oleh media berita dan mencetak ulang hasilnya dengan tajuk berikut: “Jangan berpikir! Para ilmuwan telah menemukan bahwa cuaca di akhir pekan benar-benar lebih buruk daripada di hari kerja. ” Makalah yang dikutip menyediakan statistik tentang suhu dan curah hujan selama bertahun-tahun di beberapa kota di Australia, dan memang mengungkapkan penurunan suhu pada jam-jam tertentu pada hari Sabtu dan Minggu. Setelah itu, diberikan penjelasan yang menghubungkan cuaca lokal dengan tingkat polusi udara akibat meningkatnya arus lalu lintas. Sesaat sebelum ini, penelitian serupa dilakukan di Jerman dan mengarah pada kesimpulan yang kira-kira sama.

Setuju, pecahan derajat adalah efek yang sangat halus. Mengeluh tentang cuaca buruk pada hari Sabtu yang telah lama ditunggu-tunggu, kita membahas apakah hari itu cerah atau hujan, fakta ini lebih mudah untuk didaftarkan, dan kemudian diingat, bahkan tanpa memiliki instrumen yang akurat. Kami akan melakukan penelitian kecil kami sendiri tentang topik ini dan mendapatkan hasil yang luar biasa: kami dapat dengan yakin mengatakan bahwa kami tidak tahu apakah hari dalam seminggu dan cuaca terkait di Kamchatka. Studi dengan hasil negatif biasanya tidak jatuh pada halaman majalah dan feed berita, tetapi penting bagi Anda dan saya untuk memahami atas dasar apa saya, secara umum, dapat dengan yakin mengatakan sesuatu tentang proses acak. Dan dalam hal ini, hasil negatif tidak lebih buruk daripada hasil positif.

Sepatah kata dalam membela statistik

Statistik disalahkan atas banyaknya dosa: dalam kebohongan dan kemungkinan manipulasi dan, akhirnya, dalam ketidakmampuan untuk dipahami. Tetapi saya benar-benar ingin merehabilitasi bidang pengetahuan ini, untuk menunjukkan betapa sulitnya tugas yang dimaksudkan dan betapa sulitnya untuk memahami jawaban yang diberikan statistik.

Teori probabilitas menggunakan pengetahuan yang tepat dari variabel acak dalam bentuk distribusi atau perhitungan kombinatorial yang komprehensif. Saya menekankan sekali lagi bahwa adalah mungkin untuk memiliki pengetahuan yang akurat tentang variabel acak. Tetapi bagaimana jika pengetahuan yang tepat ini tidak dapat diakses oleh kita, dan satu-satunya hal yang kita miliki adalah pengamatan? Pengembang obat baru memiliki sejumlah tes, pencipta sistem kontrol arus lalu lintas hanya memiliki serangkaian pengukuran di jalan nyata, sosiolog memiliki hasil survei, apalagi, ia dapat memastikan bahwa ketika menjawab beberapa pertanyaan, responden baru saja berbohong.

Jelas bahwa satu pengamatan tidak memberikan apa-apa sama sekali. Dua - sedikit lebih banyak daripada tidak sama sekali, tiga, empat ... seratus ... berapa banyak pengamatan yang Anda perlukan untuk mendapatkan pengetahuan tentang variabel acak yang dapat Anda yakini dengan presisi matematis? Dan pengetahuan seperti apa itu? Kemungkinan besar, itu akan disajikan dalam bentuk tabel atau histogram yang memungkinkan untuk mengevaluasi beberapa parameter dari variabel acak; mereka disebut statistik (misalnya, domain definisi, rata-rata atau varians, asimetri, dll). Mungkin melihat histogram akan dapat menebak bentuk distribusi yang tepat. Tapi perhatian! - semua hasil pengamatan itu sendiri akan menjadi variabel acak! Selama kita tidak memiliki pengetahuan yang akurat tentang distribusi, semua hasil pengamatan hanya memberi kita gambaran probabilitas dari proses acak! Deskripsi acak dari proses acak masih tidak akan bingung di sini, atau bahkan ingin membingungkan secara sengaja!

Apa yang membuat statistik matematika sebagai ilmu pasti? Metode-metodenya memungkinkan kita untuk menyimpulkan ketidaktahuan kita dalam kerangka kerja yang jelas terbatas dan memberikan ukuran kepercayaan yang dapat dihitung bahwa, dalam kerangka ini, pengetahuan kita konsisten dengan fakta. Ini adalah bahasa di mana seseorang dapat beralasan tentang variabel acak yang tidak diketahui sehingga penalaran masuk akal. Pendekatan semacam itu sangat berguna dalam filsafat, psikologi atau sosiologi, di mana sangat mudah untuk terlibat dalam penalaran dan diskusi yang panjang tanpa harapan untuk memperoleh pengetahuan positif dan, terutama, bukti. Banyak literatur dikhususkan untuk pemrosesan data statistik yang kompeten, karena itu merupakan alat yang mutlak diperlukan untuk dokter, sosiolog, ekonom, fisikawan, psikolog ... singkatnya, untuk semua ilmuwan yang meneliti apa yang disebut "dunia nyata", yang berbeda dari matematika ideal hanya pada tingkat ketidaktahuan kita tentang hal itu.

Sekarang perhatikan lagi epigraf pada bab ini dan sadari bahwa statistik, yang dengan begitu meremehkan disebut tingkat kebohongan ketiga, adalah satu-satunya hal yang dimiliki ilmu pengetahuan alam. Bukankah ini hukum utama kekejaman alam semesta! Semua hukum alam yang kita ketahui, mulai dari fisik hingga ekonomi, didasarkan pada model matematika dan sifat-sifatnya, tetapi mereka diverifikasi oleh metode statistik selama pengukuran dan pengamatan. Dalam kehidupan sehari-hari, pikiran kita membuat generalisasi dan mengamati pola, mengisolasi dan mengenali gambar berulang, ini mungkin yang terbaik yang bisa dilakukan otak manusia. Inilah yang diajarkan kecerdasan buatan akhir-akhir ini. Tetapi pikiran menyimpan kekuatannya dan cenderung untuk menarik kesimpulan dari pengamatan individu, tidak terlalu khawatir tentang keakuratan atau validitas kesimpulan ini. Pada kesempatan ini, ada pernyataan konsisten luar biasa dari buku Stephen Brast, Isola: “Semua orang menarik kesimpulan umum dari satu contoh. Setidaknya saya melakukan hal itu . " Dan sementara kita berbicara tentang seni, sifat hewan peliharaan atau mendiskusikan politik, Anda tidak bisa terlalu khawatir tentang ini. Namun, ketika membangun pesawat terbang, mengatur layanan pengiriman bandara atau menguji obat baru, Anda tidak dapat lagi merujuk pada fakta bahwa “sepertinya bagi saya”, “intuisi memberi tahu” dan “segala sesuatu terjadi dalam hidup”. Di sini Anda harus membatasi pikiran Anda pada kerangka metode matematika yang ketat.

Buku kami bukan buku teks, dan kami tidak akan mempelajari metode statistik secara terperinci dan hanya akan membatasi diri pada satu hal - teknik menguji hipotesis. Tetapi saya ingin menunjukkan arah penalaran dan bentuk hasil karakteristik dari bidang pengetahuan ini. Dan, mungkin, beberapa pembaca, calon mahasiswa, tidak hanya akan mengerti mengapa mereka menyiksanya dengan statistik, semua diagram QQ ini, distribusi t dan F, tetapi pertanyaan penting lainnya akan muncul: bagaimana mungkin mengetahui apa - pasti tentang kecelakaan? Dan apa sebenarnya yang kita pelajari menggunakan statistik?

Tiga paus statistik

Pilar utama statistik matematika adalah teori probabilitas, hukum bilangan besar, dan teorema batas pusat .

Hukum angka besar, dalam interpretasi bebas, menunjukkan bahwa sejumlah besar pengamatan variabel acak hampir pasti mencerminkan distribusinya , sehingga statistik yang diamati: rata-rata, varians, dan karakteristik lainnya cenderung menghasilkan nilai yang sesuai dengan variabel acak. Dengan kata lain, histogram dari nilai yang diamati dengan jumlah data yang tak terbatas hampir pasti cenderung ke distribusi yang dapat kita anggap benar. Hukum inilah yang menghubungkan interpretasi frekuensi "sehari-hari" probabilitas dan teoretis, sebagai ukuran dalam ruang probabilitas.

Teorema batas pusat, sekali lagi, dalam interpretasi bebas, mengatakan bahwa salah satu bentuk yang paling mungkin dari distribusi variabel acak adalah distribusi normal (Gaussian). Kata-kata yang tepat terdengar berbeda: nilai rata - rata sejumlah besar variabel acak nyata yang terdistribusi secara identik, terlepas dari distribusinya, dijelaskan oleh distribusi normal. Teorema ini biasanya dibuktikan dengan menggunakan metode analisis fungsional, tetapi kita akan melihat nanti bahwa itu dapat dipahami dan bahkan diperluas dengan memperkenalkan konsep entropi sebagai ukuran probabilitas keadaan sistem: distribusi normal memiliki entropi terbesar dengan jumlah kendala yang paling sedikit. Dalam hal ini, optimal ketika menggambarkan variabel acak yang tidak diketahui, atau variabel acak, yang merupakan kombinasi dari banyak variabel lain, distribusi yang juga tidak diketahui.

Kedua undang-undang ini mendasari estimasi kuantitatif keandalan pengetahuan kami berdasarkan pengamatan. Di sini kita berbicara tentang konfirmasi statistik atau penolakan asumsi, yang dapat dibuat dari beberapa dasar umum dan model matematika. Ini mungkin tampak aneh, tetapi dalam dirinya sendiri, statistik tidak menghasilkan pengetahuan baru. Serangkaian fakta berubah menjadi pengetahuan hanya setelah membangun hubungan antara fakta yang membentuk struktur tertentu. Struktur dan hubungan inilah yang memungkinkan kita membuat prediksi dan membuat asumsi umum berdasarkan pada sesuatu yang melampaui statistik. Asumsi semacam itu disebut hipotesis . Sudah waktunya untuk mengingat kembali salah satu hukum merfologi, dalil Persigue :

Jumlah hipotesis masuk akal yang menjelaskan fenomena apa pun tidak terbatas.

Tugas statistik matematika adalah membatasi angka tak terbatas ini, atau lebih tepatnya menguranginya menjadi satu, dan belum tentu benar sama sekali. Untuk pindah ke hipotesis yang lebih kompleks (dan seringkali lebih diinginkan), perlu, menggunakan data pengamatan, untuk membantah hipotesis yang lebih sederhana dan lebih umum, atau untuk memperkuatnya dan meninggalkan pengembangan teori lebih lanjut. Hipotesa yang sering diuji dengan cara ini disebut null , dan ada perasaan yang mendalam dalam hal ini.

Apa yang dapat bertindak sebagai hipotesis nol? Dalam arti tertentu, apa saja, pernyataan apa pun, tetapi dengan syarat bahwa itu dapat diterjemahkan ke dalam bahasa pengukuran. Paling sering, hipotesis adalah nilai yang diharapkan dari beberapa parameter, yang berubah menjadi variabel acak selama pengukuran, atau tidak adanya koneksi (korelasi) antara dua variabel acak. Terkadang diasumsikan jenis distribusi, proses acak, beberapa model matematika diusulkan. Perumusan klasik dari pertanyaan adalah sebagai berikut: apakah pengamatan memungkinkan kita untuk menolak hipotesis nol atau tidak? Lebih tepatnya, dengan kepastian apa kita dapat mengatakan bahwa pengamatan tidak dapat diperoleh berdasarkan hipotesis nol? Selain itu, jika kami tidak dapat membuktikan, berdasarkan data statistik, bahwa hipotesis nol salah, maka itu diterima sebagai benar.

Dan di sini Anda mungkin berpikir bahwa para peneliti dipaksa untuk membuat salah satu kesalahan logis klasik, yang menyandang nama Latin nyaring dan ignorantiam. Ini adalah argumen tentang kebenaran pernyataan yang didasarkan pada kurangnya bukti kepalsuannya. Sebuah contoh klasik adalah kata-kata yang diucapkan oleh Senator Joseph McCarthy ketika dia diminta untuk menyajikan fakta untuk mendukung tuduhannya bahwa seseorang tertentu adalah seorang komunis: untuk mengecualikan hubungannya dengan Komunis . " Atau bahkan lebih cerah: "Bigfoot ada, karena tidak ada yang membuktikan sebaliknya . " Mengidentifikasi perbedaan antara hipotesis ilmiah dan trik-trik serupa adalah subjek dari seluruh bidang filsafat: metodologi pengetahuan ilmiah . Salah satu hasil yang mengejutkan adalah kriteria kepalsuan , yang diajukan oleh filsuf luar biasa Karl Popper pada paruh pertama abad ke-20. Kriteria ini dirancang untuk memisahkan pengetahuan ilmiah dari tidak ilmiah, dan, pada pandangan pertama, tampaknya paradoks:

Sebuah teori atau hipotesis dapat dianggap ilmiah hanya jika ada, bahkan secara hipotesis, cara untuk membantahnya.

Apa yang bukan hukum kekejaman! Ternyata teori ilmiah apa pun secara otomatis berpotensi salah, dan teori yang benar "menurut definisi" tidak dapat dianggap ilmiah. Selain itu, ilmu-ilmu seperti matematika dan logika tidak memenuhi kriteria ini. Namun, mereka tidak mengacu pada ilmu alam , tetapi ke yang formal , yang tidak memerlukan tes untuk kepalsuan. Dan jika kita menambahkan satu hasil lagi dari waktu yang sama: Prinsip ketidaklengkapan Gödel , yang menyatakan bahwa dalam sistem formal mana pun dimungkinkan untuk merumuskan pernyataan yang tidak dapat dibuktikan atau dibantah, maka mungkin menjadi tidak jelas mengapa, secara umum, untuk terlibat dalam semua ilmu ini. Namun, penting untuk dipahami bahwa prinsip kepalsuan Popper tidak mengatakan apa-apa tentang kebenaran teori, tetapi hanya apakah itu ilmiah atau tidak. Ini dapat membantu menentukan apakah suatu teori memberikan bahasa yang masuk akal untuk berbicara tentang dunia atau tidak.

Namun, mengapa, jika kita tidak dapat menolak hipotesis berdasarkan data statistik, apakah kita berhak menerimanya sebagai benar? Faktanya adalah bahwa hipotesis statistik tidak diambil dari keinginan atau preferensi peneliti, itu harus mengikuti dari hukum formal umum. Misalnya, dari Teorema Limit Pusat, atau dari prinsip entropi maksimum. Undang-undang ini dengan tepat mencerminkan tingkat ketidaktahuan kita , tanpa menambahkan, asumsi atau hipotesis yang tidak perlu. Dalam arti tertentu, ini adalah penggunaan langsung dari prinsip filosofis terkenal yang dikenal sebagai pisau cukur Occam :

Apa yang dapat dilakukan atas dasar asumsi yang lebih sedikit tidak boleh dilakukan atas dasar lebih banyak.

Jadi, ketika kita menerima hipotesis nol, berdasarkan tidak adanya sanggahannya, kami secara formal dan jujur ​​menunjukkan bahwa sebagai hasil percobaan tingkat ketidaktahuan kami tetap pada tingkat yang sama . Dalam contoh Bigfoot, secara eksplisit atau implisit, yang terjadi adalah kebalikannya: kurangnya bukti bahwa makhluk misterius ini tampaknya bukan sesuatu yang dapat meningkatkan tingkat pengetahuan kita tentang hal itu.

Secara umum, dari sudut pandang prinsip kepalsuan, pernyataan apa pun tentang keberadaan sesuatu tidak ilmiah, karena kurangnya bukti tidak membuktikan apa-apa. Pada saat yang sama, pernyataan tentang ketiadaan sesuatu dapat dengan mudah dibantah dengan memberikan salinan, bukti tidak langsung, atau dengan membuktikan keberadaan suatu konstruksi. Dan dalam hal ini, uji hipotesis statistik menganalisis dugaan tidak adanya efek yang diinginkan dan, dalam arti tertentu, dapat memberikan penolakan yang akurat atas pernyataan ini. Inilah yang benar-benar istilah "hipotesis nol" dibenarkan sepenuhnya: ini berisi pengetahuan minimum yang diperlukan tentang sistem.

Cara membingungkan statistik dan cara menguraikan

Sangat penting untuk menekankan bahwa jika statistik menunjukkan bahwa hipotesis nol dapat ditolak, ini tidak berarti bahwa kami dengan demikian membuktikan kebenaran hipotesis alternatif apa pun.Statistik tidak boleh dikacaukan dengan logika, di situlah letak banyak kesalahan halus, terutama ketika probabilitas bersyarat untuk peristiwa dependen ikut bermain. Misalnya: sangat tidak mungkin seseorang menjadi Paus ($$~ 1 / 7 miliar) tindak dari ini bahwa Paus Yohanes Paulus II adalah bukan laki-laki? Pernyataan itu tampaknya tidak masuk akal, tetapi, sayangnya, kesimpulan yang "jelas" seperti itu sama sekali tidak benar: tes menunjukkan bahwa tes seluler untuk konten alkohol dalam darah tidak memberikan lebih banyak$\sim 1/7$$$1 % dari hasil positif palsu dan negatif palsu, oleh karena itu, dalam$1\%$$$98 % kasus, ia akan mengidentifikasi pengemudi yang mabuk dengan benar. Ayo tes$98\%$$$1000 driver dan biarkan$1000$$$100 dari mereka akan benar-benar mabuk. Hasilnya, kita dapatkan$100$$$900 × 1 % = 9 false positif dan$900\times1\%=9$$$100 × 1 % = 1 hasil negatif-negatif: yaitu, untuk satu pemabuk yang menyelinap masuk, akan ada sembilan pengemudi acak yang dituduh tidak bersalah. Apa yang bukan hukum kekejaman! Paritas akan diamati hanya jika proporsi pengemudi mabuk sama dengan$100\times1\%=1$$$1 / 2 , atau jika rasio fraksi positif palsu dan hasil negatif palsu akan dekat dengan relatif sebenarnya untuk driver mabuk mabuk. Selain itu, semakin disurvei bangsa, semakin tidak adil penggunaan perangkat yang dijelaskan oleh kita!Di sini kita dihadapkan denganperistiwa dependen. Ingat, definisi probabilitas Kolmogorov berbicara tentang metode menambahkan probabilitas menggabungkan peristiwa: probabilitas menggabungkan dua peristiwa adalah sama dengan jumlah probabilitas mereka dikurangi probabilitas persimpangan mereka. Namun, definisi-definisi ini tidak mengatakan bagaimana probabilitas persimpangan peristiwa dihitung. Untuk melakukan ini, konsep baru diperkenalkan:probabilitas bersyaratdan ketergantungan peristiwa satu sama lain muncul ke permukaan.$1/2$


Probabilitas persimpangan peristiwa A dan B didefinisikan sebagai produk dari probabilitas peristiwa B dan probabilitas peristiwa $$A , jika diketahui bahwa suatu peristiwa telah terjadi$A$$$$B$ :

$$

$$P(A \cap B) = P(B)P(A|B).$$

Sekarang Anda dapat menentukan independensi acara dalam tiga cara yang setara: Acara $$$A$ dan $$B independen jika$B$$$P ( A | B ) = P ( A ) , atau$P(A|B) = P(A)$$$P ( B | A ) = P ( B ) , atau$P(B|A) = P(B)$$$$P(A\cap B) = P(A)P(B)$ .
Ini melengkapi definisi formal probabilitas yang dimulai pada bab pertama.

Persimpangan adalah operasi komutatif, yaitu$$$P(A\cap B) = P(B\cap A)$ . Teorema Bayes segera mengikuti dari ini:

$$

$$P(A|B)P(B) = P(B|A)P(A),$$

yang dapat digunakan untuk menghitung probabilitas bersyarat.

Dalam contoh kami dengan driver dan tes alkohol, kami memiliki acara:$$A - pengemudi mabuk,$A$$$Uji B memberikan hasil positif. Peluang:$B$$$P ( A ) = 0,1 - probabilitas bahwa pengemudi yang berhenti dalam keadaan mabuk;$P(A) = 0.1$$$P ( B | A ) = 99 % - probabilitas bahwa tes akan memberikan hasil positif jika diketahui bahwa pengemudi mabuk (tidak termasuk)$P(B|A) = 99\%$$$1 % false negative)$1\%$$$P ( A | B ) = 99 % - probabilitas bahwa tes mabuk, jika tes memberikan hasil positif (dikecualikan$P(A|B) = 99\%$$$1 hasil positif palsu). Kami menghitung$1%$$$$P (B)$ - probabilitas mendapatkan hasil tes positif di jalan:

$$

$$P (B) = \ frac {P (A) P (A | B)} {P (B | A)} = P (A) = 0,1$$

Sekarang penalaran kita telah menjadi formal dan, seperti yang Anda tahu, mungkin bagi sebagian orang lebih dapat dimengerti. Konsep probabilitas bersyarat memungkinkan Anda untuk berpikir secara logis dalam bahasa teori probabilitas. Tidak mengherankan bahwa teorema Bayes telah menemukan aplikasi luas dalam teori keputusan, dalam sistem pengenalan pola, dalam filter spam, program yang menguji tes plagiarisme, dan dalam banyak teknologi informasi lainnya.

Contoh-contoh ini dipahami dengan cermat oleh siswa tentang tes medis atau praktik hukum. Tetapi, saya khawatir bahwa statistik matematika atau teori probabilitas tidak diajarkan kepada jurnalis atau politisi, tetapi mereka dengan bersemangat memohon data statistik, secara bebas menafsirkannya, dan membawa “pengetahuan” yang diperoleh kepada massa. Oleh karena itu, saya mendesak pembaca saya: Saya menemukan matematika sendiri, membantu saya mencari tahu untuk yang lain! Saya tidak melihat obat penawar lain untuk kebodohan.

Kami mengukur mudah tertipu kami

Kami akan mempertimbangkan dan menerapkan dalam praktek hanya satu dari banyak metode statistik: menguji hipotesis statistik. Bagi mereka yang telah mengaitkan kehidupan mereka dengan ilmu alam atau sosial, tidak akan ada sesuatu yang menakjubkan dalam contoh-contoh ini.

Misalkan kita berulang kali mengukur variabel acak yang memiliki nilai rata-rata $$$\ mu$ dan standar deviasi $$$\ sigma$ . Menurut Teorema Limit Pusat, nilai rata-rata yang diamati akan didistribusikan secara normal. Dari hukum jumlah besar maka rata-rata akan cenderung $$$\ mu$ , dan dari sifat-sifat distribusi normal maka setelah itu $$$n$ pengukuran, varian yang diamati dari rata-rata akan berkurang sebagai $$$\ sigma / \ sqrt {n}$ . Deviasi standar dapat dianggap sebagai kesalahan absolut dari pengukuran rata-rata, kesalahan relatif dalam kasus ini akan sama dengan $$$\ delta = \ sigma / (\ sqrt {n} \ mu)$ . Ini adalah kesimpulan yang sangat umum, terlepas dari cukup besar $$$n$ dari bentuk distribusi spesifik dari variabel acak yang diselidiki. Dua aturan bermanfaat (bukan hukum) mengikuti dari mereka:

1. Jumlah tes minimum $$$n$ harus ditentukan oleh kesalahan relatif yang diinginkan $$$\ delta$ . Apalagi kalau

$$

$$n \ geq \ kiri (\ frac {2 \ sigma} {\ mu \ delta} \ kanan) ^ 2,$$

maka probabilitas bahwa rata-rata yang diamati akan tetap dalam kesalahan yang ditentukan akan setidaknya $$$95 \%$ . Di $$$\ mu$ mendekati nol, kesalahan relatif lebih baik untuk mengganti yang absolut.

2. Biarkan hipotesis menjadi hipotesis nol bahwa mean yang diamati adalah $$$\ mu$ . Kemudian, jika rata-rata yang diamati tidak melampaui $$$\ mu \ pm 2 \ sigma / \ sqrt {n}$ , maka probabilitas bahwa hipotesis nol itu benar akan setidaknya $$$95 \%$ .


Jika diganti dalam aturan ini $$$2 \ sigma$ pada $$$3 \ sigma$ , maka tingkat kepercayaan akan meningkat menjadi $$$99,7 \%$ ini adalah aturan yang sangat kuat $$$3 \ sigma$ , yang dalam ilmu fisika memisahkan asumsi dari fakta yang ditetapkan secara eksperimental.

Akan bermanfaat bagi kita untuk mempertimbangkan penerapan aturan-aturan ini pada distribusi Bernoulli yang menggambarkan variabel acak yang mengambil tepat dua nilai, yang secara kondisional disebut "sukses" dan "kegagalan", dengan probabilitas keberhasilan yang diberikan. $$$p$ . Dalam hal ini $$$\ mu = p$ dan $$$\ sigma = \ sqrt {p (1-p)}$ , jadi untuk jumlah percobaan dan interval kepercayaan yang diperlukan kami dapatkan

$$

$$n \ geq \ frac {4} {\ delta ^ 2} \ frac {1-p} {p} \ quad dan \ quad np \ pm 2 \ sqrt {np (1-p)}.$$

Aturannya $$$2 \ sigma$ Distribusi Bernoulli dapat digunakan untuk menentukan interval kepercayaan saat merencanakan histogram. Pada dasarnya, setiap batang histogram mewakili variabel acak dengan dua nilai: "hit" - "missed", di mana probabilitas untuk memukul berhubungan dengan fungsi probabilitas yang disimulasikan. Sebagai demonstrasi, kami akan menghasilkan banyak sampel untuk tiga distribusi: seragam, geometris, dan normal, setelah itu kami membandingkan perkiraan sebaran data yang diamati dengan sebaran yang diamati. Dan di sini kita kembali melihat gema teorema batas pusat, dimanifestasikan dalam kenyataan bahwa distribusi data di sekitar nilai rata-rata dalam histogram mendekati normal. Namun, mendekati nol spread menjadi asimetris dan mendekati distribusi lain yang sangat mungkin - eksponensial. Contoh ini menunjukkan dengan baik apa yang saya maksud dengan mengatakan bahwa dalam statistik kita berurusan dengan nilai acak dari parameter variabel acak.


Contoh yang menunjukkan rasio estimasi sebaran yang dibuat oleh aturan $$$2 \ sigma$ dan penyebaran yang diamati untuk tiga variabel acak.

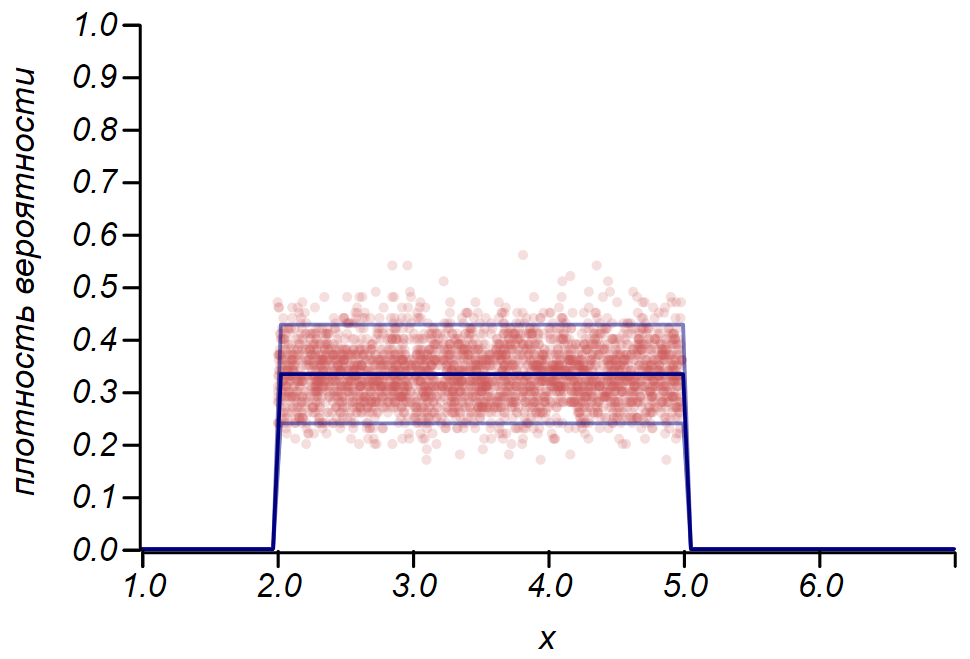
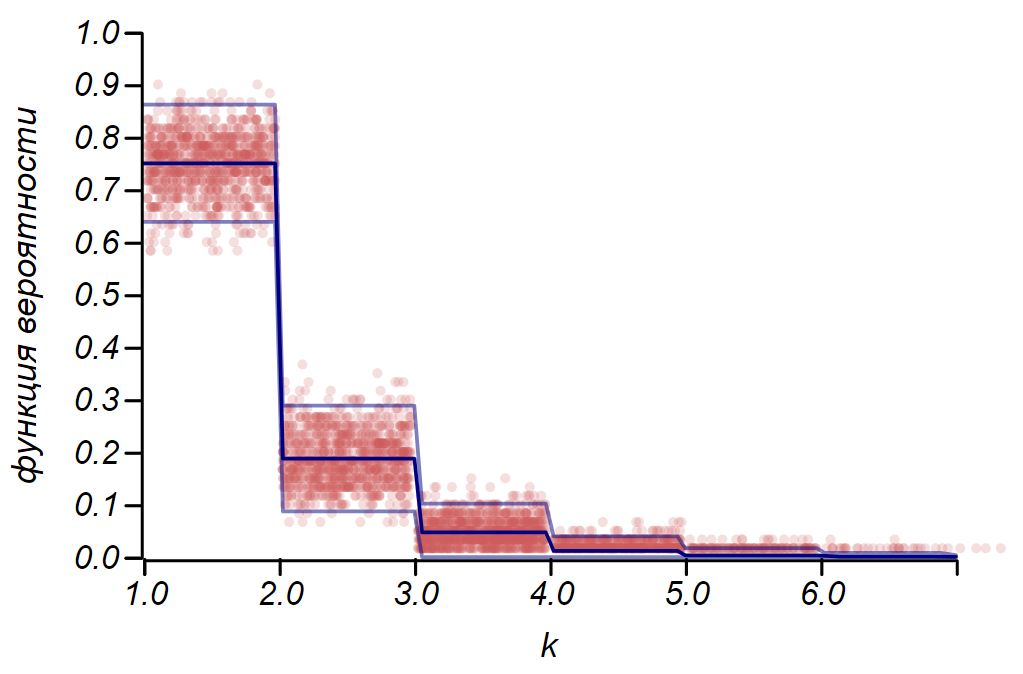
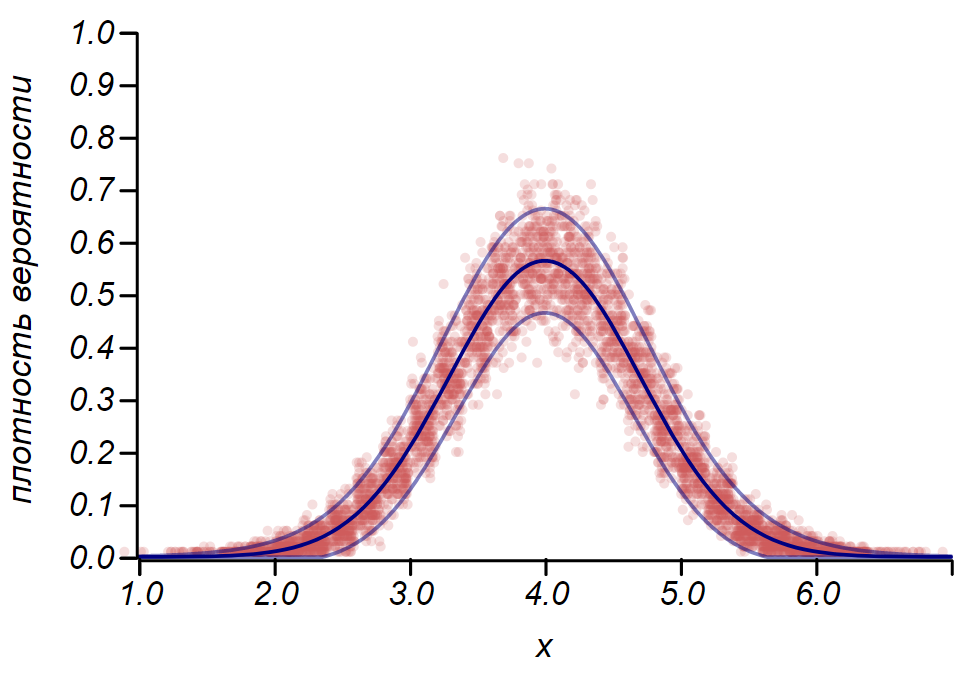
Penting untuk memahami aturan itu $$$2 \ sigma$ dan bahkan $$$3 \ sigma$ jangan selamatkan kami dari kesalahan. Mereka tidak menjamin kebenaran pernyataan apa pun, bukan bukti. Statistik membatasi tingkat ketidakpercayaan suatu hipotesis, dan tidak lebih.

Ahli matematika dan penulis mata kuliah yang sangat baik dalam teori probabilitas, Gian Carlo Rota, memberi contoh di kuliahnya di MIT. Bayangkan sebuah jurnal ilmiah yang editornya membuat keputusan dengan kemauan keras: untuk menerima publikasi secara eksklusif artikel dengan hasil positif yang memenuhi aturan $$$2 \ sigma$ atau lebih ketat. Pada saat yang sama, kolom editorial menunjukkan bahwa pembaca dapat memastikannya dengan probabilitas $$$95 \%$ pembaca tidak akan menemukan hasil yang salah di halaman majalah ini! Sayangnya, pernyataan ini dapat dengan mudah dibantah oleh alasan yang sama yang menyebabkan kita pada ketidakadilan yang mencolok saat menguji pengemudi untuk alkohol. Biarkan $$$1000$ peneliti berpengalaman $$$1000$ hipotesis, yang hanya sebagiannya benar, katakanlah, $$$10 \%$ . Berdasarkan makna pengujian hipotesis, kita dapat mengharapkan itu $$$900 \ times0.05 = $ 4$ hipotesis yang salah tidak akan ditolak secara keliru, dan akan dicatat $$$100 \ times0.95 = 95$ hasil yang benar. Total dari $$$130$ Sepertiga yang baik akan salah!

Contoh ini dengan sempurna menunjukkan hukum kekejaman domestik kita, yang belum dimasukkan dalam antologi merfologi, hukum Chernomyrdin :

Kami menginginkan yang terbaik, tetapi ternyata, seperti biasa.

Mudah untuk mendapatkan estimasi umum dari persentase hasil yang salah yang akan dimasukkan dalam masalah jurnal, dengan asumsi bahwa bagian dari hipotesis yang benar adalah $$$0 <\ alpha <1$ dan probabilitas menerima hipotesis yang salah adalah $$$p$ :

$$

$$x = \ frac {(1- \ alpha) p} {\ alpha (1-p) + (1- \ alpha) p}.$$

Area yang membatasi bagian dari hasil yang salah yang sengaja dipublikasikan dalam jurnal diperlihatkan dalam gambar.

Perkiraan persentase publikasi yang berisi hasil yang jelas salah ketika mengadopsi berbagai kriteria untuk menguji hipotesis. Dapat dilihat bahwa menerima hipotesis berdasarkan aturan $$$2 \ sigma$ bisa berisiko sementara kriterianya $$$4 \ sigma$ sudah bisa dianggap sangat kuat.

Tentu saja kita tidak tahu ini. $$$\ alpha$ , dan kita tidak akan pernah tahu, tetapi tentu saja kurang dari satu, yang berarti bahwa, dalam hal apapun, pernyataan dari kolom editorial tidak dapat dianggap serius. Anda dapat membatasi diri pada kriteria yang kaku $$$4 \ sigma$ tetapi membutuhkan sejumlah besar tes. Oleh karena itu, perlu untuk meningkatkan pangsa hipotesis sejati dalam serangkaian asumsi yang mungkin. Pendekatan standar dari metode ilmiah kognisi ditujukan untuk ini - konsistensi logis dari hipotesis, konsistensi mereka dengan fakta dan teori yang telah membuktikan penerapannya, bergantung pada model matematika dan pemikiran kritis.

Dan lagi tentang cuaca

Pada awal bab ini, kami berbicara tentang fakta bahwa akhir pekan dan cuaca buruk lebih sering terjadi bersamaan daripada yang kami inginkan. Mari kita coba selesaikan studi ini. Setiap hari hujan dapat dianggap sebagai pengamatan dari variabel acak - hari dalam seminggu mematuhi distribusi Bernoulli dengan probabilitas $$$1/7$ . Mari kita asumsikan, sebagai hipotesis nol, asumsi bahwa semua hari dalam seminggu adalah sama dalam hal cuaca dan hujan dapat menghujani mereka dengan kemungkinan yang sama. Kami memiliki dua hari libur, jadi kami mendapatkan probabilitas yang diharapkan dari kebetulan hari yang buruk dan hari libur yang sama $$$2/7$ , nilai ini akan menjadi parameter distribusi Bernoulli. Seberapa sering hujan? Pada waktu yang berbeda dalam setahun, tentu saja dengan cara yang berbeda, tetapi di Petropavlovsk-Kamchatsky, rata-rata, ada sembilan puluh hari hujan atau bersalju dalam setahun. Jadi arus hari dengan curah hujan memiliki intensitas sekitar $$$90/365 \ approx1 / 4$ . Mari kita hitung berapa akhir pekan hujan yang harus kita daftarkan untuk memastikan ada beberapa pola. Hasilnya ditunjukkan dalam tabel.

Periode pengamatan	musim panas	tahun	$$$5$ tahun
Jumlah Pengamatan yang Diharapkan	$$$23$	$$$90$	$$$456$
Jumlah Hasil Positif yang Diharapkan	$$$6$	$$$26$	$$$130$
Penyimpangan yang signifikan	$$$4$	$$$9$	$$$19$
Proporsi yang signifikan dari yang buruk total jumlah hari libur	$$$42 \%$	$$$33 \%$	$$$29 \%$

Apa angka-angka ini bicarakan? Jika menurut Anda bahwa selama setahun berturut-turut telah terjadi "tidak ada musim panas", batu jahat itu mengejar akhir pekan Anda dengan mengirimkan hujan kepada mereka, ini dapat diperiksa dan dikonfirmasi. Namun, selama musim panas, batu jahat bisa ditangkap hanya jika lebih dari dua perlima dari seluruh akhir pekan ternyata hujan. Hipotesis nol menunjukkan bahwa hanya seperempat akhir pekan harus bertepatan dengan cuaca buruk. Dalam lima tahun pengamatan, seseorang sudah bisa berharap untuk melihat penyimpangan halus yang melampaui $$$5 \%$ dan, jika perlu, lanjutkan dengan penjelasan mereka.

Saya mengambil keuntungan dari buku harian cuaca sekolah, yang diadakan dari 2014 hingga 2018, dan mengetahui apa yang terjadi selama lima tahun ini $$$459$ hari-hari hujan mereka $$$141$ jatuh pada akhir pekan. Ini, memang, lebih dari jumlah yang diharapkan oleh $$$11$ hari, tetapi penyimpangan yang signifikan dimulai dengan $$$19$ hari, jadi ini, seperti yang kita katakan di masa kecil: "tidak masuk hitungan." Berikut adalah serangkaian data dan histogram yang menunjukkan distribusi cuaca buruk menurut hari dalam seminggu. Garis horisontal dalam histogram menunjukkan interval di mana penyimpangan acak dari distribusi seragam dapat diamati untuk jumlah data yang sama.


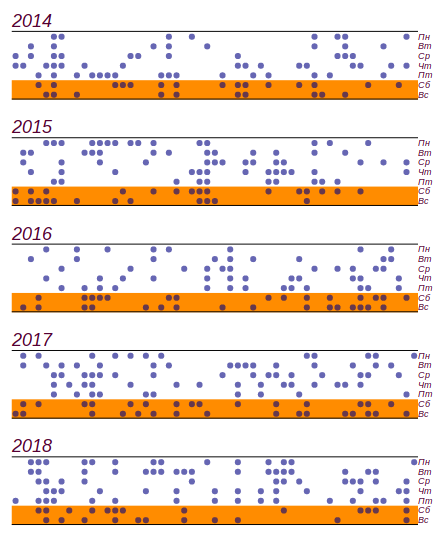
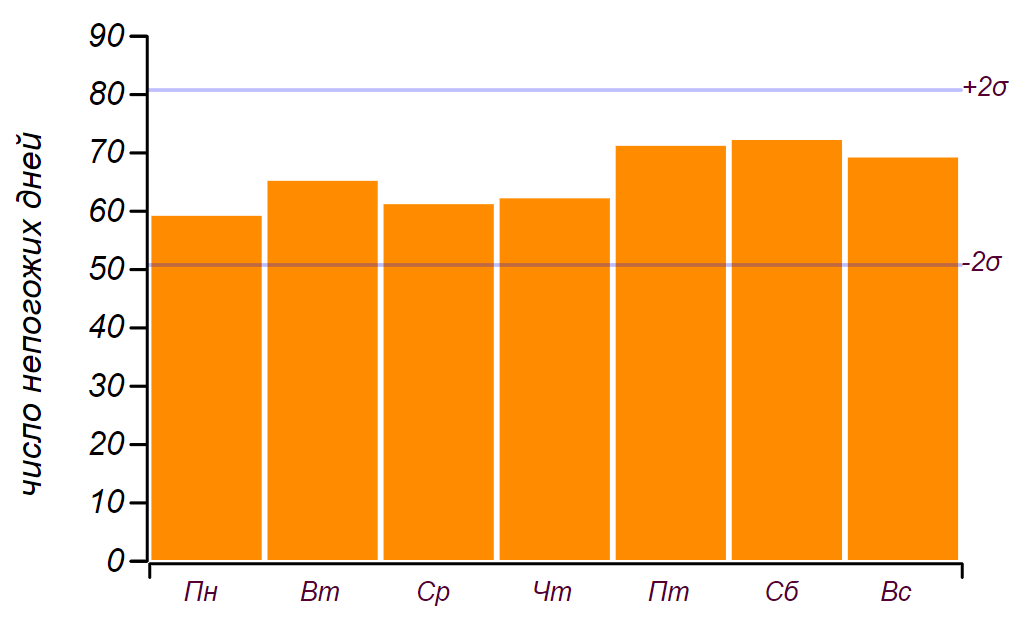Rangkaian data awal dan distribusi hari buruk berdasarkan hari dalam seminggu diperoleh selama lima tahun pengamatan.

Dapat dilihat bahwa sejak hari Jumat, memang telah terjadi peningkatan jumlah hari dengan cuaca buruk. Tetapi prasyarat tidak cukup untuk menemukan alasan untuk pertumbuhan ini: hasil yang sama dapat diperoleh hanya dengan memilah-milah angka acak. Kesimpulan: selama lima tahun mengamati cuaca, saya mengumpulkan hampir dua ribu catatan, tetapi tidak belajar sesuatu yang baru tentang distribusi cuaca pada hari-hari dalam seminggu.

Ketika Anda melihat entri buku harian, jelas terbukti bahwa cuaca tidak datang sendiri, tetapi dalam periode dua hingga tiga hari atau bahkan siklon mingguan. Apakah ini entah bagaimana mempengaruhi hasilnya? Anda dapat mencoba untuk mempertimbangkan pengamatan ini, dan menganggap bahwa hujan turun rata-rata selama dua hari (pada kenyataannya, $$$1,7$ hari), maka kemungkinan memblokir akhir pekan meningkat menjadi $$$3/7$ . Dengan probabilitas seperti itu, jumlah pertandingan yang diharapkan selama lima tahun seharusnya $$$195 \ pm21$ , mis. dari $$$174$ sebelumnya $$$216$ kali. Nilai yang diamati $$$141$ tidak termasuk dalam kisaran ini dan, oleh karena itu, hipotesis efek cuaca buruk dua hari dapat ditolak dengan aman. Apakah kita mempelajari sesuatu yang baru? Ya, kami belajar: tampaknya fitur yang jelas dari proses ini tidak memerlukan efek apa pun. Ini layak dipertimbangkan, dan kami akan melakukannya nanti. Tetapi kesimpulan utama adalah bahwa tidak ada alasan untuk mempertimbangkan efek yang lebih halus, karena pengamatan dan, yang paling penting, jumlah mereka, secara konsisten berbicara mendukung penjelasan paling sederhana.

Tapi ketidaksenangan kita bukan statistik lima tahun atau bahkan tahunan, ingatan manusia tidak begitu lama. Sayang sekali saat hujan turun pada akhir pekan tiga atau empat kali berturut-turut! Seberapa sering ini dapat diamati? Apalagi jika Anda ingat bahwa cuaca buruk tidak datang sendiri. Tugas tersebut dapat dirumuskan sebagai berikut: “Berapa probabilitas itu $$$n$ akhir pekan berturut-turut akan hujan? " Masuk akal untuk berasumsi bahwa cuaca buruk membentuk aliran Poisson dengan intensitas $$$1/4$ . Ini berarti bahwa rata-rata, seperempat hari dari periode apa pun akan buruk. Mengamati hanya akhir pekan, kita tidak boleh mengubah intensitas aliran, dan dari semua akhir pekan cuaca buruk seharusnya, rata-rata, juga seperempat. Jadi, kami mengemukakan hipotesis nol: aliran cuaca buruk adalah Poisson, dengan parameter yang diketahui, yang berarti bahwa interval antara peristiwa Poisson dijelaskan oleh distribusi eksponensial. Kami tertarik pada interval diskrit: $$$0, \ 1, \ 2, \ 3$ hari, dll. oleh karena itu kita dapat menggunakan analog diskrit dari distribusi eksponensial - distribusi geometrik dengan parameter $$$1/4$ . Gambar tersebut menunjukkan apa yang kami lakukan dan dapat dilihat bahwa asumsi bahwa kami mengamati proses Poisson tidak masuk akal untuk ditolak.


Distribusi yang diamati dari panjang rantai akhir pekan yang gagal dan teoritis. Garis tipis menunjukkan penyimpangan yang diizinkan untuk jumlah pengamatan yang kita miliki.

Anda dapat bertanya pada diri sendiri pertanyaan ini: berapa tahun Anda perlu melakukan pengamatan sehingga perbedaan dalam $$$11$ hari bisa dengan yakin dikonfirmasi atau ditolak sebagai penyimpangan acak? Sangat mudah untuk menghitung: probabilitas yang diamati $$$141/459 = 0,307$ berbeda dari yang diharapkan $$$2/7 = $ 0,28$ pada $$$0,02$ . Untuk merekam perbedaan dalam seratus, kesalahan absolut tidak lebih dari $$$0,005$ itu membuat $$$1,75 \%$ dari ukuran yang diukur. Dari sini kita mendapatkan ukuran sampel yang diperlukan $$$n \ geq (4 \ cdot 5/7) / (0,0175 ^ 2 \ cdot 2/7) \ sekitar 32000$ hari hujan. Itu akan memakan waktu sekitar $$$4 \ cdot 32000/365 \ sekitar 360$ tahun pengamatan meteorologi terus menerus, karena hanya setiap hari keempat hujan atau salju. Sayangnya, ini lebih dari waktu Kamchatka adalah bagian dari Rusia, jadi saya tidak punya kesempatan untuk mencari tahu bagaimana hal-hal itu "benar-benar". Terutama jika Anda memperhitungkan bahwa selama waktu ini iklim berhasil berubah secara dramatis - dari Zaman Es Kecil, alam muncul pada optimum berikutnya.

Jadi bagaimana para peneliti Australia berhasil mencatat deviasi suhu dalam fraksi derajat dan mengapa masuk akal untuk mempertimbangkan studi ini? Faktanya adalah bahwa mereka menggunakan data suhu per jam yang tidak "menipis" oleh proses acak apa pun. Begitu seterusnya $$$30$ pengamatan meteorologi selama bertahun-tahun berhasil mengumpulkan lebih dari seperempat juta bacaan, yang memungkinkan untuk mengurangi deviasi standar rata-rata $$$500$ kali sehubungan dengan deviasi suhu harian standar. Ini cukup untuk berbicara tentang akurasi dalam sepersepuluh derajat. Selain itu, penulis menggunakan metode lain yang indah yang mengkonfirmasi keberadaan siklus waktu: pencampuran acak dari deret waktu. Pencampuran tersebut mempertahankan sifat statistik, seperti intensitas aliran, namun, "menghapus" pola temporal, menjadikan proses tersebut benar-benar Poisson. Perbandingan banyak seri sintetik dan eksperimental memungkinkan kami untuk memverifikasi bahwa penyimpangan yang diamati dari proses dari Poisson adalah signifikan. Dengan cara yang sama, ahli seismologi A. A. Gusev menunjukkan bahwa gempa bumi di wilayah mana pun membentuk sejenis aliran yang mirip dengan sifat-sifat pengelompokan. Ini berarti bahwa gempa bumi cenderung mengelompok dalam waktu, membentuk segel aliran yang sangat tidak menyenangkan. Belakangan ternyata urutan letusan gunung berapi besar memiliki sifat yang sama.

Sumber keacakan lainnya

Tentu saja, cuaca, seperti gempa bumi, tidak dapat dijelaskan oleh proses Poisson - ini adalah proses dinamis di mana kondisi saat ini adalah fungsi dari yang sebelumnya. Mengapa pengamatan cuaca mingguan kami mendukung model stokastik sederhana? Faktanya adalah bahwa kami menampilkan proses pembentukan curah hujan secara teratur selama tujuh hari, atau, berbicara dalam bahasa matematika, pada sistem deduksi modulo tujuh . Proses proyeksi ini mampu menghasilkan kekacauan dari serangkaian data yang tertata dengan baik. Dari sini, misalnya, ada keacakan terlihat dalam urutan digit notasi desimal dari sebagian besar bilangan real.

Kita sudah bicara tentang bilangan rasional, yang dinyatakan sebagai bilangan bulat bilangan bulat. Mereka memiliki struktur internal, yang ditentukan oleh dua angka: pembilang dan penyebut. Tetapi ketika menulis dalam bentuk desimal, Anda dapat mengamati lompatan dari keteraturan dalam representasi angka seperti $$$1/2 = 0,5 \ overline {0}$ , atau $$$1/3 = 0. \ Overline {3}$ untuk pengulangan berkala dari urutan yang sudah cukup acak dalam angka seperti $$$1/17 = 0. \ Overline {0588235294117647}$ . Bilangan irasional tidak memiliki notasi desimal terbatas atau periodik, dan dalam hal ini, kekacauan paling sering terjadi dalam urutan angka. Tetapi ini tidak berarti bahwa tidak ada urutan dalam angka-angka ini! Misalnya, bilangan irasional pertama yang ditemui oleh matematikawan $$$\ sqrt {2}$ dalam notasi desimal menghasilkan set angka acak. Namun, di sisi lain, angka ini dapat direpresentasikan sebagai fraksi lanjutan tanpa batas:

$$

$$\ sqrt {2} = 1 + \ frac {1} {2+ \ frac {1} {2+ \ frac {1} {2+ ...}}}.$$

Sangat mudah untuk menunjukkan bahwa rantai ini memang sama dengan akar dua dengan menyelesaikan persamaan:

$$

$$x-1 = \ frac {1} {2+ (x-1)}.$$

Fraksi lanjutan dengan koefisien berulang ditulis sesaat, seperti fraksi desimal berkala, misalnya: $$$\ sqrt {2} = [1, \ bar {2}]$ , $$$\ sqrt {3} = [1, \ overline {1,2}]$ . Rasio emas yang terkenal dalam hal ini adalah bilangan irasional yang paling sederhana: $$$\ varphi = [1, \ bar {1}]$ . Semua bilangan rasional direpresentasikan dalam bentuk fraksi lanjutan yang terbatas, beberapa irasional - dalam bentuk tak terbatas, tetapi secara berkala, mereka disebut aljabar , sama yang tidak memiliki notasi terbatas bahkan dalam bentuk ini - transendental . Yang paling terkenal dari transendental adalah jumlahnya $$$\ pi$ , ia menciptakan kekacauan baik dalam desimal maupun dalam bentuk pecahan lanjutan: $$$\ pi \ kira-kira [3, 7,15,1,292,1,1,1,2,1,3,1,14,2,1, ...]$ . Dan ini nomor Euler $$$e$ sisa transendental, dalam bentuk fraksi lanjutan, menampilkan struktur internal yang tersembunyi dalam notasi desimal: $$$e \ kira-kira [2,1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...]$ .

Mungkin bukan seorang ahli matematika, dimulai dengan Pythagoras, yang curiga dunia licik, menemukan apa yang dibutuhkan, bilangan fundamental semacam itu. $$ p i begitu halus struktur kacau kompleks. Tentu saja, itu dapat direpresentasikan sebagai jumlah dari seri numerik yang cukup elegan, tetapi seri ini tidak secara langsung berbicara tentang sifat nomor ini dan mereka tidak universal. Saya percaya bahwa matematikawan masa depan akan menemukan beberapa representasi baru bilangan, seuniversal fraksi lanjutan, yang akan mengungkapkan urutan ketat yang disembunyikan oleh alam dalam bilangan.$\ pi$

$$

$$*\ *\ *$$

Hasil bab ini, sebagian besar, negatif. Dan sebagai penulis yang ingin mengejutkan pembaca dengan pola tersembunyi dan penemuan tak terduga, saya ragu apakah itu harus dimasukkan dalam buku. Tetapi pembicaraan kami tentang cuaca masuk ke topik yang sangat penting - nilai dan keberartian pendekatan ilmu alam.

Seorang gadis yang bijak, Sonya Shatalova, yang memandang dunia melalui prisma autisme, pada usia sepuluh memberikan definisi yang sangat ringkas dan tepat: "Sains adalah sistem pengetahuan yang didasarkan pada keraguan". Dunia nyata tidak stabil dan berusaha bersembunyi di balik kompleksitas, keacakan yang terlihat, dan pengukuran yang tidak dapat diandalkan. Keraguan dalam ilmu alam tidak bisa dihindari. Matematika tampaknya merupakan bidang kepastian, di mana, tampaknya, orang bisa melupakan keraguan. Dan sangat menggoda untuk bersembunyi di balik tembok kerajaan ini; pertimbangkan alih-alih model dunia yang tidak dapat dikenali yang dapat diselidiki secara menyeluruh; hitung dan hitung, manfaat formula siap mencerna apa saja. Namun demikian, matematika adalah ilmu dan keraguan di dalamnya adalah kejujuran internal yang mendalam yang tidak memberikan istirahat sampai konstruksi matematika dibersihkan dari asumsi tambahan dan hipotesis yang tidak perlu. Dalam bidang matematika, mereka berbicara bahasa yang kompleks, tetapi harmonis, cocok untuk alasan tentang dunia nyata. Sangat penting untuk membiasakan diri dengan bahasa ini,untuk mencegah angka-angka meniru statistik, untuk tidak membiarkan fakta berpura-pura menjadi pengetahuan, dan untuk ketidaktahuan dan manipulasi kontras ilmu nyata.