Ringkasan
Deskripsi diberikan tentang undang-undang yang ditetapkan dalam daftar berurutan semua solusi untuk masalah distribusi n-Queens. Ditetapkan bahwa:
- Proporsi solusi lengkap dalam daftar umum semua solusi menurun, dengan meningkatnya nilai n.
- Solusi lengkap didistribusikan dalam daftar berurutan dari semua solusi sedemikian rupa sehingga solusi lengkap yang terletak berdekatan satu sama lain dalam daftar paling mungkin ditemukan.
- Ada simetri dalam urutan solusi lengkap dalam daftar umum semua solusi. Jika pada posisi ke-i dari awal daftar solusi selesai, maka solusi simetris dari akhir daftar yang terletak di posisi n-i + 1 juga lengkap (aturan simetri solusi).
- Setiap pasangan solusi, baik pendek dan lengkap, terletak secara simetris dalam daftar semua solusi, saling melengkapi - jumlah indeks posisi dari garis yang sesuai adalah konstan dan sama dengan n +1 (aturan saling melengkapi solusi). Ini menunjukkan bahwa hanya paruh pertama dari daftar semua solusi lengkap yang "unik", solusi lengkap dari paruh kedua daftar dapat diperoleh berdasarkan aturan saling melengkapi. Konsekuensi dari aturan ini adalah kenyataan bahwa untuk setiap nilai n, jumlah solusi lengkap akan selalu menjadi bilangan genap.
- Aktivitas sel-sel dari baris-baris matriks solusi simetris sehubungan dengan sumbu horizontal yang melewati tengah-tengah matriks ini. Ini berarti bahwa aktivitas sel-sel pada baris ke-i selalu bertepatan dengan aktivitas sel-sel pada baris ke-1 + 1. Aktivitas adalah frekuensi yang dengannya indeks sel muncul pada baris yang sesuai dari daftar solusi lengkap. Demikian pula, aktivitas sel-sel kolom dari matriks solusi simetris tentang sumbu vertikal yang membagi matriks menjadi dua bagian yang sama besar.
- Terlepas dari n, dalam pencarian berurutan semua solusi, solusi lengkap pertama hanya muncul setelah urutan tertentu dari solusi singkat. Ukuran urutan awal solusi singkat meningkat dengan n. Panjang daftar solusi pendek sebelum munculnya solusi lengkap pertama untuk nilai genap n secara signifikan lebih lama daripada untuk nilai ganjil terdekat.
- Garis dalam matriks keputusan, di mana kesulitan mulai bergerak maju, dan keputusan pendek pertama terbentuk, membagi matriks sesuai dengan aturan rasio emas. Untuk nilai n yang kecil, kesimpulan seperti itu merupakan perkiraan, namun, dengan peningkatan nilai n, keakuratan kesimpulan tersebut secara asimptotik meningkat ke tingkat aturan standar.
Publikasi ini menyajikan hasil utama dari artikel [1] , yang diterbitkan dalam jurnal "Modeling of Artificial Intelligence, 2018, 5 (1)". Di Habré ada pekerjaan yang berhubungan dengan masalah n-Queens: [2] , [3] ,
Masalah mendistribusikan n ratu pada papan catur berukuran nxn memiliki sejarah panjang. Awalnya dirumuskan pada tahun 1848 oleh M. Bezzel [4] sebagai tugas intelektual untuk papan catur biasa. Seiring waktu, pernyataan masalah diperluas oleh F. Nauck [5], dan ukuran papan catur dapat mengambil nilai apa pun.
Pendahuluan
Pernyataan masalahnya cukup sederhana: Anda perlu mendistribusikan n ratu di papan catur berukuran nxn sehingga di setiap baris, setiap kolom, dan juga diagonal kiri dan kanan yang melewati sel tempat ratu berada, tidak ada lebih dari satu ratu. Tugas ini mudah dimengerti atau dijelaskan kepada seseorang, tetapi agak sulit untuk menyelesaikannya. Faktanya adalah bahwa tidak ada aturan atas dasar di mana Anda dapat mengatur ratu pada setiap baris untuk mendapatkan solusi. Suatu solusi hanya dapat diperoleh dengan menyebutkan berbagai varian dari susunan ratu pada baris tertentu. Namun, kompleksitas metode solusi ini terletak pada kenyataan bahwa jumlah semua varian pengaturan ratu meningkat secara eksponensial dengan meningkatnya n. Selain itu, dengan mengambil langkah ke depan untuk menempatkan ratu dalam posisi bebas dari baris tertentu mengarah ke perubahan dalam daftar posisi bebas di baris yang tersisa, dan ketika kembali satu langkah, untuk membentuk cabang pencarian, perlu untuk membersihkan jejak tindakan yang dilakukan sebelumnya.
Ada sejumlah besar publikasi yang terkait dengan berbagai aspek penyelesaian masalah n-Queens. Mereka dapat dikaitkan dengan beberapa bidang penelitian: pencarian untuk semua solusi lengkap untuk nilai tertentu dari ukuran papan catur (n), pengembangan algoritma cepat untuk menemukan satu solusi untuk nilai yang berbeda dari n, solusi dari masalah lengkap untuk solusi lengkap, untuk komposisi sewenang-wenang k queens, pertanyaan kompleksitas perhitungan perhitungan algoritmik, serta berbagai modifikasi dari perumusan asli masalah. Untuk membiasakan diri dengan bidang-bidang ini, saya akan merekomendasikan publikasi yang menarik oleh B. Jordan, S. Brett [6] dan IP Gent, C. Jefferson, P. Nightingale [7], yang memberikan gambaran yang cukup rinci dari berbagai bidang penelitian. Dari catatan khusus adalah publikasi Internet [8] yang didukung oleh Walter Costers, yang disiapkan oleh kelompok dari Universiteit Leiden dan berisi tautan ke 342 publikasi yang berkaitan dengan masalah n-queens (per Desember 2018).
Meskipun masalah n-Queens tetap aktif selama lebih dari 150 tahun, dan sejumlah besar publikasi telah muncul selama waktu ini, saya tidak dapat menemukan pekerjaan yang akan relevan dengan pencarian pola dalam hasil penyelesaian masalah ini. Sebagian besar proyek yang terkait dengan pencarian semua solusi kemungkinan besar tidak menyimpan solusi yang ditemukan dan tidak melihat apa yang ada di dalam. Di sana, dalam penetapan tugas ada tujuan dominan lainnya, dan rekan kerja kami yang terhormat mencapainya. Namun, dari jarak jauh, bagi saya situasinya mirip dengan ketika seseorang merebus telur untuk sarapan, tetapi tidak memakannya, tetapi membuangnya, hanya menyisakan jumlah telur rebus dalam ingatannya. Saya selalu yakin bahwa jika datanya tidak acak, maka harus ada keteraturan tertentu di dalamnya, bahkan jika kita tidak dapat menemukan keteraturan ini. Keyakinan inilah yang menjadi alasan pencarian pola dalam tugas ini.
Seiring dengan keinginan untuk memberikan anggota komunitas Habr informasi yang berguna untuk dipikirkan, saya ingin programmer berbakat, yang sebagian besar di Habr, untuk lebih memperhatikan arah pengembangan seperti simulasi komputer (Simulasi Komputasi). Sebagai metode penelitian, "Matematika Algoritmik" seperti itu digunakan pada "keunggulan" banyak bidang: Kecerdasan Buatan, Ilmu Perangkat Lunak, Ilmu Data, ... dan saya yakin bahwa masalah yang sangat kompleks dan penting untuk aplikasi praktis akan diselesaikan berdasarkan matematika algoritmik jika tidak.
Definisi
Selanjutnya, kami akan menunjukkan ukuran papan catur dengan simbol n. Sebuah solusi akan disebut lengkap jika semua n queens secara konsisten ditempatkan di papan catur. Semua solusi lain, ketika jumlah ratu yang ditempatkan dengan benar kurang dari n - kami akan memanggil solusi singkat. Dengan panjang solusi, kami berarti jumlah (k) ratu yang ditempatkan dengan benar. Jumlah semua solusi, untuk nilai n yang diberikan, akan dilambangkan dengan m. Sebagai analog dari "papan catur" ukuran nx n., Kami akan mempertimbangkan "matriks solusi" ukuran nx n.
Mulai
Untuk melakukan penelitian, suatu algoritma dikembangkan untuk mencari semua solusi untuk nilai arbitrer n. Kami tidak menggunakan rekursi standar atau sistem loop bersarang seperti biasa. Untuk nilai n yang besar, pendekatan seperti itu akan cukup bermasalah. Algoritma ini dibangun berdasarkan serangkaian peristiwa yang saling berinteraksi, di mana masing-masing sistem tindakan berlangsung, saling berhubungan. Hal ini memungkinkan untuk hanya menerapkan mekanisme untuk mengubah ruang keadaan saat memilih node berikutnya di cabang solusi masalah (Forward tracking), atau membersihkan jejak tindakan yang dilakukan sebelumnya, ketika kembali satu langkah atau lebih (Back tracking). Tidak ada persyaratan khusus untuk ukuran memori atau kecepatan prosesor dalam algoritma.
Berdasarkan algoritma ini, semua solusi sekuensial (baik pendek dan lengkap) untuk berbagai nilai dari matriks solusi n = (7, ..., 16) ditemukan. Karena ukuran daftar solusi lengkap adalah urutan bernama The On-Line Encyclopedya of Integer Sequences (urutan A000170 [9]) dan ditunjukkan dalam banyak publikasi, tampaknya menarik bagi saya untuk membuat daftar ukuran semua solusi (pendek + penuh) untuk nilai n yang dipertimbangkan oleh kami: 7 (194), 8 (736), 9 (2 936), 10 (12 774), 11 (61 076), 12 (314 730), 13 (1 716 652), 14 (10 030 692), 15 ( 62 518 772), 16 (415 515 376).
Selanjutnya, dengan menggunakan solusi yang ditemukan, kami memberikan kata-kata dari beberapa masalah, metode untuk menyelesaikannya dan deskripsi hasil.
1. Ruang keadaan di mana solusi dicari
Pencacahan berbagai opsi untuk pengaturan ratu dalam baris tertentu dari matriks keputusan ukuran n mengarah pada pembentukan ruang keadaan. Jika tidak ada larangan pengaturan ratu dalam satu atau sel lain dari matriks, maka ukuran ruang keadaan akan n n . Jika kita hanya memperhitungkan aturan yang melarang lokasi lebih dari satu ratu di setiap baris dan setiap kolom, maka kita akan mendapatkan beberapa bagian dari ruang negara yang ukurannya akan n! Himpunan bagian dari ruang keadaan ini berhubungan dengan masalah distribusi n oleh benteng. Jika, bersama dengan ini, kami juga mempertimbangkan aturan yang melarang lokasi lebih dari satu ratu diagonal kiri dan kanan melewati sel tempat ratu berada, maka kami mendapatkan beberapa ruang pencarian yang ukurannya akan kurang dari n .. Kami menyebutnya subset ruang negara - ruang pencarian yang produktif, berdasarkan pada fakta bahwa hanya dalam subruang ini semua solusi yang mungkin. Setiap cabang yang selesai di ruang pencarian produktif adalah solusi dengan sejumlah ratu yang ditempatkan dengan benar. Pada dasarnya, ini adalah keputusan singkat, dan hanya sebagian kecil yang tersisa adalah keputusan lengkap.
Gambar 1 menunjukkan grafik logaritma natural dari tiga indikator: a) nilai faktorial (n!) Pada ukuran matriks keputusan; b) jumlah semua keputusan (pendek dan lengkap); c) jumlah solusi lengkap, tergantung pada ukuran matriks solusi (n). Seperti yang diharapkan, semua kurva ditandai oleh peningkatan eksponensial dengan meningkatnya n. Tingkat pertumbuhan jumlah semua solusi dan jumlah solusi lengkap berbeda, meskipun ini tidak begitu terlihat pada grafik, karena ukuran sampel yang kecil dari nilai n. Misalnya, untuk n = 13, perbedaan antara logaritma indikator ini adalah 3,148, dan untuk n = 16 perbedaan ini meningkat sebesar 0,190 dan 3,338. Jelas, dengan peningkatan n lebih lanjut, perbedaan ini akan lebih signifikan.

Gambar. 1 Ketergantungan logaritma ukuran ruang keadaan pada nilai n
2. Bagaimana proporsi keputusan lengkap dalam daftar umum semua keputusan berubah?
Jelas, jika laju pertumbuhan jumlah solusi lengkap jauh di belakang laju pertumbuhan jumlah semua solusi, maka probabilitas menemukan solusi lengkap dalam daftar umum semua solusi akan menurun dengan meningkatnya nilai n. Gambar 2 menunjukkan grafik proporsi solusi lengkap dalam daftar umum semua solusi pada nilai n. Terlihat bahwa dengan peningkatan ukuran matriks solusi, bagian dari semua solusi lengkap dalam daftar umum berkurang. Untuk nilai awal n = (7, ..., 14), nilai ini menurun 5,66 kali dari nilai 0,2062 menjadi 0,0364, dan kemudian penurunan bertahap, asimptotik pada nilai ini berlanjut. Di sini kontradiksi formal muncul antara dua pernyataan: di satu sisi, jumlah solusi lengkap meningkat secara eksponensial dengan meningkatnya n, dan di sisi lain, probabilitas solusi lengkap dalam daftar berurutan dari semua solusi terus menurun. Paradoks yang tampak ini dijelaskan dengan sangat sederhana, ukuran ruang produktif dan ukuran yang terkait dari daftar semua solusi tumbuh lebih cepat dengan meningkatnya n daripada jumlah solusi lengkap. Ini seperti mencoba menemukan jarum di tumpukan jerami - jumlah jerami "dengan meningkatnya n" tumbuh lebih cepat daripada jumlah jarum yang hilang di sana. Oleh karena itu, kita dapat mengasumsikan bahwa jika untuk n = 27, jumlah solusi lengkap adalah sekitar 2.346 * 10 17 , maka nilai yang sesuai dari jumlah semua solusi kemungkinan besar akan menjadi 3-4 pesanan yang besarnya lebih besar dari ~ 10 20
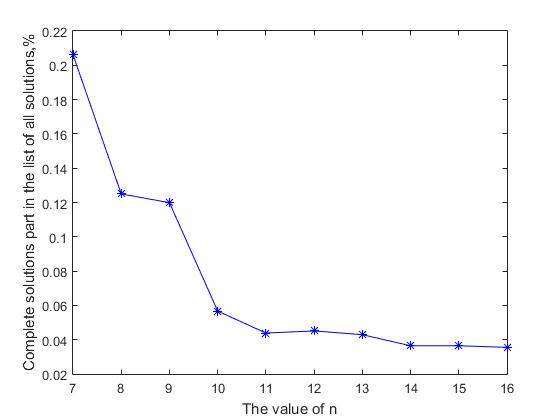
Gbr. 2 Mengurangi proporsi solusi lengkap dalam daftar umum semua solusi dengan meningkatnya n
3. Berapa frekuensi solusi dari berbagai panjang dalam daftar semua solusi?
Seperti disebutkan sebelumnya, semua cabang selesai di ruang pencarian produktif adalah solusi dengan jumlah ratu yang berbeda ditempatkan dengan benar.
Sangat menarik bagi kami dengan frekuensi apa ada solusi dari berbagai panjang dalam daftar umum semua solusi.
Tabel 1 untuk nilai n = (7, ..., 12) menyajikan nilai yang sesuai dari frekuensi relatif untuk solusi yang memiliki panjang yang berbeda. Representasi visual yang sesuai dari data ini ditunjukkan pada Gambar 3.
Analisis tabel memungkinkan kita untuk menarik kesimpulan berikut:
a) untuk setiap matriks ukuran n, ada panjang tertentu dari solusi yang memiliki frekuensi maksimum (disorot dalam huruf tebal).
Tabel 1. Frekuensi relatif (%) dari solusi dengan panjang yang berbeda (k) untuk matriks ukuran n = (7, ..., 12)
| n \ k | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|
| 7 | 10.31 | 31.23 | 27.84 | 20.62 | | | | | |
| 8 | 2.45 | 20.38 | 34,78 | 29,89 | 12.50 | | | | |
| 9 | 0,34 | 5.79 | 21.73 | 35.83 | 34.32 | 11.99 | | | |
| 10 | 0,05 | 1.35 | 8.41 | 25.62 | 32,94 | 25.96 | 5.67 | | |
| 11 | | 0,15 | 2.12 | 11.80 | 26.71 | 34.47 | 20.36 | 4.39 | |
| 12 | | 0,01 | 0,29 | 3.28 | 13.56 | 29.88 | 31.29 | 17.18 | 4.51 |
b) dengan meningkatnya n, jumlah solusi dengan panjang berbeda meningkat. Dengan demikian, frekuensi relatif semua keputusan menurun.
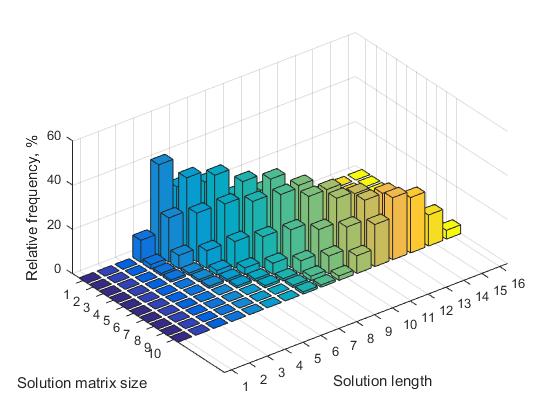
Gambar. 3 Frekuensi solusi dari berbagai panjang tergantung pada ukuran matriks solusi, n = 7, ..., 16
c) untuk setiap matriks ukuran n, ada ukuran minimum tertentu dari panjang solusi, di bawah ini tidak ada solusi singkat. Dengan meningkatnya n, nilai ambang ini meningkat. Misalnya, untuk n = 8, nilai ambang adalah 4, masing-masing, untuk n = 16, nilai ambang adalah 7.
4. Apa pengaturan relatif dari solusi lengkap dalam daftar berurutan semua solusi?
Dalam pernyataan masalah "pada distribusi n ratu" tidak ada alasan yang akan memberikan alasan untuk membuat asumsi tentang urutan keputusan lengkap dalam daftar umum semua solusi. Kami tertarik pada apakah solusi lengkap dalam daftar umum didistribusikan secara merata, acak, atau jika memiliki beberapa kekhasan. Untuk mengetahuinya, kami menganalisis jarak antara solusi lengkap terdekat dalam daftar berurutan semua solusi. Seperti dapat dilihat dari Gambar 4, di mana untuk n = 12, grafik perubahan dalam frekuensi yang sesuai disajikan,
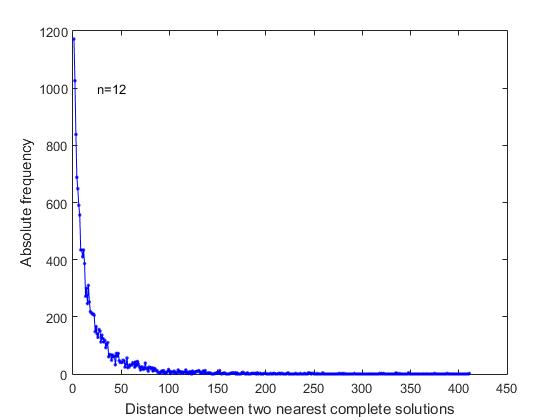
Gambar. 4 Frekuensi versus jarak antara solusi lengkap terdekat dalam daftar berurutan dari semua solusi lengkap (n = 12)
dengan frekuensi terbesar ada solusi lengkap yang segera mengikuti satu sama lain dalam daftar urutan umum semua solusi. Ini adalah kasus pembentukan cabang pencarian ketika hubungan posisi bebas di baris terakhir memungkinkan Anda untuk membentuk dua atau lebih solusi lengkap berturut-turut. Lebih jauh, frekuensi maksimum adalah solusi lengkap yang ada di antaranya: satu solusi pendek, dua solusi pendek, dll.
5. Apakah ada pola dalam pengaturan solusi lengkap dalam daftar umum semua solusi?
Untuk menjawab pertanyaan ini, kami telah menganalisis daftar berurutan dari semua solusi untuk nilai n = (7, ..., 16). Untuk menunjukkan dengan jelas hasilnya, pada Gambar 5, untuk nilai n = 8, sebuah grafik disajikan di mana panjang setiap solusi dalam daftar semua 736 solusi ditunjukkan secara berturut-turut. Di sini, hanya 92 solusi yang lengkap dan mereka disorot dalam warna merah, sisanya 644 solusi pendek dan disorot dengan warna biru. Dapat dilihat bahwa solusi lengkap tidak terdistribusi secara merata dalam daftar semua solusi. Ada area di mana solusi lengkap lebih umum, dan ada tempat di mana solusi lengkap jarang atau tidak sama sekali.

Gambar. 5 Panjang setiap solusi dalam daftar berurutan dari semua solusi, untuk matriks 8 x 8 (solusi merah-penuh, solusi biru-pendek). Jumlah total semua solusi adalah 736
Namun, ada hal lain yang penting di sini. Jika Anda hati-hati melihat sosok yang menyerupai barcode biru-merah, Anda akan melihat satu fitur yang sangat penting, semua garis merah simetris sehubungan dengan beberapa garis vertikal bersyarat yang melewati bagian tengah daftar solusi. Faktanya, seperti yang ditunjukkan oleh cek, jika pada langkah ke-i dari awal daftar umum ada solusi lengkap, maka, solusi yang lengkap pasti akan ditemukan pada langkah m-i +1. Misalnya, untuk n = 8, jika solusi lengkap pertama dalam pencarian sekuensial untuk semua solusi muncul di langkah 43, maka, solusi lengkap terakhir dalam daftar akan ditemukan di langkah 736-43 + 1 = 694. Jika solusi ke-17 untuk matriks 10x10 muncul dalam daftar pada langkah 368, maka solusi lengkap simetris untuk itu muncul dalam daftar semua solusi pada langkah 12774-17 + 1 = 12407. Aturan ini berlaku untuk matriks keputusan dengan ukuran berapa pun. Karena itu, kita dapat merumuskan aturan. Untuk nilai n apa pun, jika dalam daftar urutan semua solusi, pada posisi ke-i dari awal daftar, solusinya selesai, maka solusi simetris dari akhir daftar yang terletak di posisi m-i + 1 juga akan lengkap (aturan simetri solusi). m, , . , n, , . ( – ).
, – . n+1 . , 17- n=10 368- (1, 5, 7, 10, 4, 2, 9, 3, 6, 8).
, 12407 (10, 6, 4, 1, 7, 9, 2, 8, 5, 3). , (11, 11, …,11). n, , , . . n, ( , ), , – n+1 ( ). Q(i ) Q1(i) – ,
<b>`Q ( i ) + Q1 ( i ) = n + 1, i = (1, n) `</b>
Aturan ini berarti bahwa jika solusi lengkap diperoleh pada langkah ke- i , maka solusi lengkap simetris pada langkah m-i +1 menjadi diketahui . Oleh karena itu, ketika mencari semua solusi lengkap, cukup untuk menemukan hanya separuh pertama dari semua solusi lengkap. Paruh kedua dari daftar solusi lengkap dapat ditentukan dari solusi yang sudah diperoleh, berdasarkan aturan saling melengkapi. Kriteria bahwa setengah dari daftar solusi lengkap dicapai adalah pemenuhan aturan saling melengkapi antara solusi lengkap sebelumnya Q (i-1) dan Q berikutnya (i) . yaitu, perlu bahwa jumlah setiap pasangan indeks yang sesuai dari dua solusi berturut-turut sama dengan n +1 . Karena setiap solusi lengkap dari daftar semua solusi lengkap adalah unik, hanya solusi lengkap yang berurutan yang akan saling melengkapi yang ada di kedua sisi perbatasan yang membagi daftar menjadi dua.
Kedua aturan ini akan memungkinkan di masa mendatang, ketika mencari semua solusi lengkap untuk nilai n berikutnya, untuk mengurangi jumlah perhitungan dan, karenanya, waktu perhitungan setengahnya.
6. Visualisasi urutan langkah-langkah untuk menemukan solusi lengkap pertama
Bagaimana proses melakukan langkah maju (Pelacakan maju) dan pengembalian kembali (Pelacakan balik) saat membentuk cabang pencarian solusi? Untuk menjawab pertanyaan ini, kami, untuk matriks 10 x 10, menentukan urutan dari 194 transisi awal antara garis sampai solusi lengkap pertama muncul. Grafik yang sesuai ditunjukkan pada Gambar 6. Garis biru menunjukkan gerakan maju, dan garis merah menunjukkan pengembalian. Selama 194 langkah ini, 35 solusi singkat telah dibuat. Gambar tersebut menunjukkan bahwa sebagian besar transisi (84,5%) terjadi di antara garis (5, 6, 7, 8). Ini adalah semacam "bottleneck" dalam perjalanan ke "goal". Sebagai berikut dari gambar, hanya ada 7 kasus beralih ke baris 4 dan satu kasus beralih ke baris ketiga. Ada juga 13 kasus beralih ke garis ke-9. Tiga upaya untuk pindah ke baris ke-10 tidak berhasil, karena di cabang pencarian di baris ke-10 tidak ada posisi kosong. Contoh ini menunjukkan semua cabang pendek

Gambar. 6 Visualisasi peristiwa Pelacakan Kembali (merah) dan Pelacakan Lanjutan (biru) untuk 194 langkah pencarian pertama (n = 10)
solusi, hingga solusi lengkap pertama. Algoritma apa pun untuk memecahkan masalah seperti itu akan efektif jika berisi mekanisme yang akan menghilangkan semua (atau bagian) cabang yang mengarah ke solusi singkat.
7. Setelah berapa banyak keputusan singkat yang muncul, solusi lengkap pertama kali muncul?
Mempertimbangkan bahwa solusi lengkap muncul secara berbeda pada bagian yang berbeda dari daftar semua solusi, tampaknya penting untuk mengetahui berapa banyak solusi singkat yang muncul dalam solusi lengkap pertama saat mencari semua solusi secara berurutan. Untuk tujuan ini, untuk nilai-nilai n = (7, ..., 35), semua solusi singkat dihitung secara berturut-turut sampai kemunculan solusi lengkap pertama. Seperti dapat dilihat dari Gambar 7, yang menunjukkan grafik ketergantungan pada n, logaritma natural dari nomor langkah, ketika solusi lengkap pertama muncul, untuk nilai genap n, solusi lengkap pertama muncul lebih lambat daripada nilai ganjil terdekat dari n. Misalnya, untuk nilai ganjil n = 21, solusi lengkap pertama muncul di langkah 3138, dan untuk nilai genap berikutnya n = 22, solusi lengkap pertama muncul di langkah 628169. Dengan demikian, untuk nilai ganjil berikutnya n = 23, solusi lengkap pertama muncul pada langkah 9155.

Gbr. 7 Jumlah solusi pendek hingga solusi lengkap pertama, untuk berbagai nilai n
Jumlah langkah iterasi untuk genap n = 22 adalah 200,2 dan 68,6 kali lebih banyak, masing-masing, daripada nilai ganjil terdekat. Ini sangat jelas dalam menghitung waktu untuk n = 34. Di sini, solusi lengkap pertama muncul di 826 337 langkah 184, dan untuk nomor ganjil terdekat (33, 35), masing-masing di 50 704 900 dan 84 888 759 langkah. Juga harus dikatakan tentang pelanggaran pertumbuhan monoton dari jumlah solusi singkat sebelum munculnya solusi lengkap pertama, dengan meningkatnya n. Untuk nilai genap n, ini terjadi pada n = 19, untuk nilai ganjil, pada n = 24 dan n = 26.
8. Apakah frekuensi sel dari setiap baris dalam daftar semua solusi lengkap sama?
Matriks keputusan berukuran nxn, yang berfungsi sebagai analog papan catur, seperti adegan di mana semua peristiwa terjadi. Setiap solusi lengkap yang terbentuk pada adegan ini terdiri dari indeks sel dari baris yang berbeda, karena setiap sel tersebut adalah simpul dalam cabang pencarian solusi. Pertanyaan yang menarik bagi kami adalah sebagai berikut: apakah beban di setiap baris sama untuk sel yang berbeda saat membuat daftar semua solusi lengkap? Jelas, semakin tinggi nilai frekuensi, semakin tinggi aktivitas sel ini dalam membentuk daftar solusi lengkap. Untuk menetapkan ini, kami menentukan untuk setiap baris, berdasarkan daftar semua solusi lengkap, frekuensi relatif dari berbagai indeks. Pertama, kami menganalisis untuk matriks solusi ukuran n = 8. Mari kita periksa setiap baris array solusi lengkap secara berurutan dan menentukan frekuensi berbagai nilai indeks. Tabel 2 menunjukkan nilai yang sesuai dari frekuensi aktivitas absolut dari sel yang berbeda di masing-masing dari delapan baris, dan pada Gambar. 8
Tabel 2. Frekuensi absolut dari aktivitas sel di masing-masing dari delapan baris matriks keputusan 8x8, berdasarkan analisis daftar semua solusi lengkap
| baris \ col | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 | 4 | 8 | 16 | 18 | 18 | 16 | 8 | 4 |
| 2 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 3 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 4 | 18 | 8 | 12 | 8 | 8 | 12 | 8 | 18 |
| 5 | 18 | 8 | 12 | 8 | 8 | 12 | 8 | 18 |
| 6 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 7 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 8 | 4 | 8 | 16 | 18 | 18 | 16 | 8 | 4 |
sekelompok 4 grafik disajikan, di mana setiap grafik mencirikan perubahan dalam frekuensi relatif dalam satu baris. Salah satu kesimpulan penting yang fundamental yang dapat diambil dari analisis semua data yang diperoleh adalah sebagai berikut:
- untuk matriks keputusan ukuran sewenang-wenang n , aktivitas sel-sel dari baris ke- i bertepatan dengan aktivitas sel n-i + 1 , yaitu. aktivitas sel-sel dari baris pertama selalu bertepatan dengan aktivitas sel-sel dari baris terakhir, masing-masing, aktivitas sel-sel dari baris kedua bertepatan dengan aktivitas sel-sel dari baris kedua dari belakang, dll.
Jika n ganjil, hanya baris median dari matriks solusi yang tidak memiliki pasangan simetris, untuk semua sel lainnya, aturan di atas valid. - Kami menyebutnya "properti simetri horizontal dari aktivitas sel-sel dari berbagai baris matriks solusi" . Untuk alasan ini, kami menyajikan hanya 4 grafik untuk matriks keputusan ukuran n = 8, karena grafik aktivitas sel yang sesuai untuk baris (1, 8), (2,7), (3,6) dan (4,5) sepenuhnya identik.
Juga harus dicatat bahwa nilai frekuensi simetris tentang sumbu vertikal yang membagi matriks menjadi dua bagian yang sama (dalam kasus nilai genap n), atau melewati kolom median (dalam kasus nilai ganjil n). Kami menyebutnya "properti simetri vertikal dari aktivitas sel-sel dari berbagai baris matriks solusi" .
Selain itu, sebagai berikut dari analisis Tabel 2, frekuensi dalam matriks solusi simetris sehubungan dengan diagonal utama kiri dan kanan.
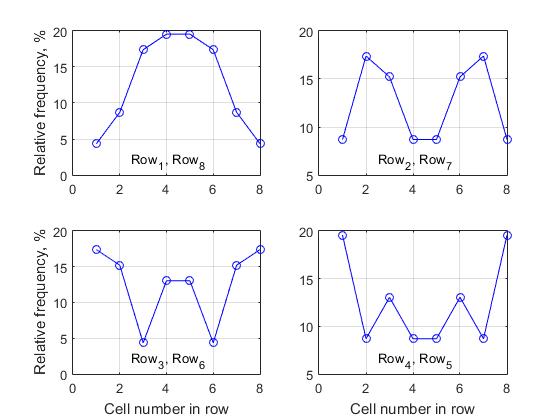
Gbr. 8 Aktivitas sel pada baris yang sesuai saat membentuk daftar solusi lengkap, n = 8
Saya pikir bahwa adanya aturan restriktif dalam pernyataan masalah, dan properti terkait non-determinisme, "membentuk" semacam hubungan harmonis antara node dalam garis yang berbeda. Cabang-cabang pencarian yang sesuai dengan aturan ini - mengarah pada pembentukan solusi lengkap. Cabang-cabang pencarian yang tersisa, pada beberapa langkah, melanggar aturan-aturan ini, dan sebagai hasilnya, "menyelesaikan perjalanan mereka" dalam bentuk keputusan singkat. Perlu dicatat di sini bahwa sel-sel matriks keputusan hanya memiliki hubungan lokal dalam kelompok pengaruh proyeksi, tidak ada aturan yang ditentukan untuk tindakan terkoordinasi di antara mereka. Aktivitas kolektif sel hanyalah konsekuensi dari pengaruh pengaruh aturan restriktif. Oleh karena itu, pertanyaan yang agak menarik tetap terbuka, bagaimana aturan restriktif, seperti faktor non-determinisme, mempengaruhi sel-sel matriks keputusan, yang pada akhirnya mengarah pada pembentukan matriks aktivitas sel yang “harmonis” - simetris sehubungan dengan sumbu horizontal dan vertikal, serta sehubungan dengan kiri. dan diagonal utama kanan. Apakah ini sifat khas dari masalah ini saja, atau apakah itu berlaku untuk masalah non-deterministik lainnya?
9. Dari nomor baris manakah algoritma Forward tracking - Back tracking diaktifkan?
Jika kami mengikuti operasi algoritme pemilihan baris berurutan dalam matriks keputusan untuk lokasi ratu, Anda akan melihat bahwa mulai dari baris tertentu, yang akan kami sebut "StopRow", pengereman "forward" terjadi. Di cabang pencarian, ini adalah baris pertama di mana ada masalah dengan ketersediaan gratis

Fig. 9-1 Ketergantungan rasio indeks StopRow ke n pada ukuran matriks keputusan (bagian-1)
posisi untuk lokasi ratu. Dari baris ini, algoritma Pelacakan Kembali dihidupkan untuk menghapus jejak tindakan yang dilakukan sebelumnya dan kembali. Ini adalah garis di mana solusi singkat pertama muncul.
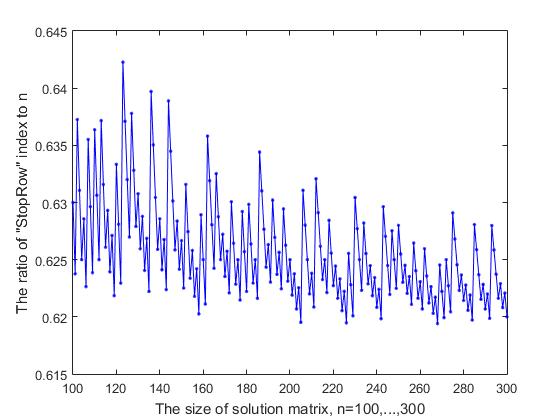
Gambar 9-2 Ketergantungan rasio indeks StopRow ke n pada ukuran matriks keputusan (bagian-2)
Indeks garis "StopRow", yang kesulitannya mulai bergerak maju, tergantung pada ukuran n dari matriks keputusan. Jika kita mempertimbangkan rasio indeks ini, yang kita tunjukkan dengan StopInd dengan ukuran matriks solusi n, maka, seperti yang dapat dilihat dari Gambar 9-1, di mana hasil perhitungan untuk nilai awal n = (7, ..., 99) disajikan, rasio ini berfluktuasi ke tingkat yang lebih besar atau lebih kecil samping dan cenderung menurun. Dengan peningkatan n = (100, ..., 300), rasio ini berfluktuasi antara 0,619 - 0,642 (Gbr. 9-2), dan dengan peningkatan lebih lanjut dalam n, kami mendapatkan hasil berikut (nilai n diberikan secara berurutan, dan nilai dalam kurung adalah Rasio StopInd dan StopInd / n: 1000 (619, 0,6190), 2000 (1239, 0,6195), 3000 (1856, 0,6187), 4000 (2473, 0,6182), 5000 (3091, 0,6182), yang mengejutkan, dapat dikatakan bahwa berhenti itu -line membagi matriks keputusan berdasarkan aturan rasio emas : yaitu, rasio StopInd / n berbeda dari (n-StopInd) / StopInd dengan jumlah kecil yang cenderung nol dengan meningkatnya n. Misalnya, untuk n = 5000 perbedaan antara hubungan 3091/5000 dan 1909/3091 adalah 0,006, yang kurang dari 0,1% dari rata-rata dua hubungan ini.
Grafik yang ditunjukkan dalam dua gambar 9- (1,2) memiliki bentuk variabilitas non-acak, yang menyerupai rekaman pada "stave musikal". Lompatan berulang dan jatuh bertahap terlihat dengan periodisitas yang tidak teratur. Jelas, ada beberapa alasan untuk perilaku kurva semacam ini, dan mungkin ini akan menarik untuk diteliti. Untuk alasan ini, untuk tujuan visualisasi yang lebih rinci, grafik disajikan dalam dua gambar.
Saya menganggap hanya sebagian dari pertanyaan yang dapat dirumuskan berdasarkan hasil dari solusi masalah "pada distribusi n-queens." Saya berharap bahwa hasil yang diperoleh akan membuat mekanisme pembentukan proses non-deterministik dan perubahan dalam ruang negara lebih transparan untuk pemahaman. Mungkin ini akan berfungsi sebagai titik tumpu untuk perumusan tugas-tugas baru dan bergerak maju.
Kesimpulan
- Jika, melihat publikasi, kita telah mencapai suatu kesimpulan, maka secara alami pertanyaan akan muncul: "apa arti Solusi Masalah Satu Miliar Ratu dalam judul artikel?" Dalam menyiapkan publikasi untuk Habr, saya berpikir bahwa seseorang yang, misalnya, memiliki tambang di mana berlian ditambang, harus memberikan setidaknya satu berlian masing-masing kepada teman dan kerabatnya, jika tidak maka itu tidak adil. Oleh karena itu, saya ingin memberikan hadiah kepada semua anggota komunitas habr: peserta, penyelenggara, pengunjung. Seperti namanya, ini adalah solusi untuk masalah mendistribusikan satu miliar ratu pada papan catur berukuran miliar miliar.
Tentu saja, ini bukan intan, tetapi bagi para pecinta seni intelektual sejati, ini bisa lebih berharga daripada "semacam intan di sana." Selain itu, berlian sangat berbeda di seluruh dunia, dan solusi ini hanya dalam satu salinan sejauh ini. Dan Dewa Byte kami (*) melihat bahwa saya melakukan ini dengan tulus.
Solusi yang dihasilkan adalah array satu dimensi dari satu miliar angka, yang disajikan dalam format MatLab .mat dan tersedia di: Solusi Masalah Satu Miliar Queens di Google Drive
-Elemen pertama dari array ini mencirikan posisi ratu di baris pertama, elemen kedua - posisi di baris kedua, dll. Ini hanyalah satu solusi dari nBillion solusi yang mungkin. Dan nilai nBillion sedemikian besar sehingga dapat dianggap sebagai kerabat dekat tak terhingga.
- Tampaknya bagi saya bahwa solusi ini dapat dikaitkan dengan kategori nilai intelektual virtual. Kita dapat mengatakan bahwa "ini adalah sesuatu di mana ada sesuatu." Mereka benar-benar tidak dapat "disentuh", jadi itu dirasakan dalam kesadaran hanya pada tingkat sensasi. Sebenarnya, ada tatanan yang luar biasa dan harmoni yang eksplisit dan implisit. Ini adalah hadiah simbolis murni (harfiah dan kiasan) yang ditujukan kepada semua anggota komunitas. Saya pikir, " Kamu tidak seperti orang lain ."
(Saya harap seseorang "membawa pulang hadiah itu." File ini cukup besar - 3,7 Gb. Ini bersih, data terverifikasi. Google Drive akan menampilkan peringatan - perlakukan ini dengan pemahaman)
- Sebelum membuat keputusan ini, saya memikirkan sifat kolektif-kolektif dari hadiah semacam itu. Mungkinkah seseorang akan diberikan yang asli, dan sisanya dengan salinan? Tapi solusinya sederhana. Konsep "sehari-hari" yang biasa "asli" dan "menyalin", dalam hal ini, kehilangan artinya. Kami tidak menyalin, tetapi membuat yang asli. Dan "aslinya" adalah sama untuk semua dan setara.
- Saya pikir di perusahaan kerabat, Anda kemungkinan besar akan menjadi satu-satunya yang menerima "produk intelektual" sebagai hadiah. Akan menyenangkan jika Anda memberi tahu ibu mertua Anda tentang hadiah semacam itu: "Bayangkan seorang ibu dengan papan catur berukuran 50.000 km per 50.000 km, di mana 1 miliar ratu didistribusikan sedemikian rupa sehingga orang tidak melihat yang lain dalam jarak dekat ...". Siapa tahu, mungkin setelah ini, menantu laki-laki akan lebih dihargai, karena ia diberikan hadiah aneh.
Saya berharap semua anggota komunitas kesehatan habr, sukses dan sejahtera. Semoga tahun baru membawa keberuntungan bagi kita semua.
(*) - Karena mengacu pada nama objek, uraiannya juga harus diberikan.
Byte God berarti entitas multidimensi, yang terdiri dari nol dan satu, masuk akal dalam segala hal dan tak terbatas di semua arah. Setiap urutan nol dan satu di ruang ini mewakili pengetahuan tertentu.
Referensi
[4] Max Bezzel, Proposal masalah 8-ratu ", Berliner Schachzeitung, Volume
3 (1848), halaman 363. (Diserahkan dengan nama penulis \ Schachfreund ".)
[5] Franz Nauck, Briefwechseln mit allen fur alle ", Illustrirte Zeitung, Volume
377 Nomor 15 (1850), halaman 182.
[6] Bell Jordan; Stevens Brett (2009). "Survei hasil yang diketahui dan daerah penelitian untuk n-ratu." Matematika Terpisah. 309 (1): 1–31
[7] Gent, Ian P.; Jefferson, Christopher; Nightingale, Peter (Agustus 2017). "Kompleksitas Penyelesaian n-Queens". Jurnal Penelitian Kecerdasan Buatan. AAAI Press. 59: 815–848
[8] W. Kosters dan semua, n-Queens - 342 referensi, (20 November 2018)
[9] NJA Sloane, Ensiklopedia On-Line dari Urutan Integer, diterbitkan secara elektronik. 2016