Model Matematika Kekacauan

Pendahuluan

Habr sudah membahas teori chaos dalam artikel [1,2,3]. Aspek-aspek teori chaos berikut dipertimbangkan dalam artikel-artikel ini: diagram umum generator Chua; memodelkan dinamika sistem Lorentz; penarik yang diprogram oleh sirkuit terintegrasi logika Lorentz, Ressler, Rikitake dan Nose-Hoover.

Namun, teknik teori chaos juga digunakan untuk memodelkan sistem biologis, yang, tidak diragukan lagi, adalah salah satu sistem yang paling kacau dari semua yang dapat dibayangkan. Sistem pemerataan dinamis digunakan untuk memodelkan segala sesuatu mulai dari populasi dan pertumbuhan epidemi hingga detak jantung aritmia [4].

Bahkan, hampir semua sistem kacau dapat dimodelkan - pasar sekuritas menghasilkan kurva yang dapat dengan mudah dianalisis menggunakan penarik aneh, proses menjatuhkan tetes dari keran bocor adalah acak ketika dianalisis dengan telinga telanjang, tetapi jika digambarkan sebagai penarik aneh, itu membuka tatanan supernatural yang tidak bisa diharapkan dari cara tradisional.

Tujuan artikel ini adalah untuk menguji teori kekacauan menggunakan contoh peningkatan jumlah populasi biologis dan menggandakan siklus dalam sistem mekanis dengan visualisasi grafis model matematika berdasarkan program intuitif sederhana yang ditulis dengan Python.

Artikel ini ditulis untuk tujuan pengajaran, tetapi akan memungkinkan bahkan pembaca tanpa pengalaman pemrograman untuk menggunakan program-program di atas untuk secara mandiri menyelesaikan sebagian besar masalah pendidikan baru pada topik pemodelan fenomena kekacauan.

Menggandakan periode siklus dan kekacauan pada contoh pertumbuhan jumlah populasi biologis

Mari kita mulai dengan melihat persamaan diferensial logistik yang memodelkan peningkatan terbatas daripada eksponensial dalam jumlah populasi biologis:

$$$\ frac {dN} {dt} = aN-bN ^ {2}, (a, b> 0). (1)$

Persamaan inilah yang dapat memprediksi pola perilaku eksotis dan tak terduga dari beberapa populasi. Memang menurut (1), untuk $$$t \ rightarrow + \ infty$ ukuran populasi mendekati batas sama dengan a / b .

Untuk solusi numerik dari solusi diferensial logistik, seseorang dapat menggunakan algoritma paling sederhana, dengan nilai numerik dari langkah waktu, $$$t_ {n + 1} = t_ {n} + h$ , maka solusi (1) dapat diperoleh dengan berulang kali menerapkan relasi berikut:

$$$N_ {n + 1} = N_ {n} + (aN_n-bN {_ {n}} ^ {2}) h.$ (2)

Kami mewakili persamaan (2) dalam bentuk persamaan logistik dalam perbedaan hingga:

$$$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$ . (3)

di mana: r = 1 + ah dan s = bh .
Pergantian dalam (3) $$$N_ {n} = \ frac {r} {s} x_ {n}$ kami mendapatkan formula berulang:

$$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ , (4)

Menghitung nilai yang diberikan oleh relasi (3), kita dapat menghasilkan urutan $$$x_ {1}, x_ {2}, x_ {3}, .....$
nilai maksimum dari jumlah populasi yang akan didukung oleh lingkungan pada waktu tertentu $$$t_ {1}, t_ {2}, t_ {3}.$ .

Kami berasumsi bahwa ada nilai pembatas fraksi yang menyatakan bagian dari ukuran populasi:

$$$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$ , (5).

Kami akan menyelidiki bagaimana hal itu tergantung $$$x _ {\ infty}$ dari parameter pertumbuhan r dalam persamaan (4). Untuk melakukan ini, dengan Python, kita menulis sebuah program yang dimulai dengan $$$x_ {1} = $ 0,$ menghitung hasil pada beberapa ratus iterasi ( n = 200 ) untuk r = 1,5; 2.0; 2.5 :


Hasil program (untuk mengurangi output dari hasil, tiga nilai pertama dan empat terakhir diberikan):

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000 

Analisis model diskrit menunjukkan bahwa untuk r = 1.5; 2.0; 2.5 dengan peningkatan jumlah iterasi, nilainya $$$x_ {n}$ menstabilkan dan menjadi hampir sama dengan batas $$$x _ {\ infty}$ , yang ditentukan oleh relasi (5). Apalagi untuk nilai yang diberikan r, kuantitas $$$x _ {\ infty}$ sama dengan itu $$$x _ {\ infty} = 0,3333; 0,5000; $ 0,600$ .
Kami meningkatkan r = 3.1; 3.25; 3.5 dan jumlah iterasi n = 1008, untuk ini kami membuat perubahan berikut pada program:


Hasil program (untuk mengurangi output dari hasil, empat nilai pertama dan delapan terakhir diberikan):

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269 

Sebagai berikut dari data di atas, alih-alih stabil di dekat populasi tunggal yang membatasi, bagian fraksional dari populasi berfluktuasi antara dua fraksi seiring perubahan waktu. Dibandingkan dengan r = 3,1 , periode siklus untuk r = 3,25 dua kali lipat, dan untuk r = 3,5 empat kali.


Hasil dari program:



Karena menggandakan periode iterasi, $$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ menjadi dikenal luas. Ketika nilai tingkat pertumbuhan melebihi r = 3,56 , penggandaan periode dipercepat dan kekacauan ekstrem sudah muncul pada titik r = 3,57 . Untuk menampilkan awal kekacauan, kami menggunakan program berikut:


Hasil dari program:

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397 

Kami akan menulis sebuah program untuk memvisualisasikan ketergantungan perilaku iterasi pada parameter pertumbuhan r . Untuk setiap nilai r dalam interval $$$a \ leqslant r \ leqslant b$ 1000 iterasi dilakukan untuk mencapai stabilitas. Kemudian, setiap 250 nilai yang diperoleh sebagai hasil dari iterasi diplot sepanjang sumbu vertikal, membentuk titik ( r, x ):


Hasilnya berupa diagram:



Grafik yang dihasilkan disebut "diagram cabang" , yang memungkinkan Anda untuk menentukan apakah nilai r tertentu sesuai dengan siklus atau kekacauan. Satu-satunya nilai ukuran populasi ditentukan oleh nilai tersebut $$$r \ sekitar 3$ kemudian siklus dengan periode 2 hingga $$$r \ sekitar 3,4$ , kemudian siklus dengan periode 4, kemudian siklus dengan periode 8 dan seterusnya dengan pendekatan cepat untuk kekacauan.

Perlu dicatat bahwa area vertikal dari ruang tidak terisi pada grafik adalah daerah r = 3,6 dan r = 3,7 , antara r = 3,7 dan r = 3,8 , antara r = 3,8 dan r = 3,9 di mana urutan siklik kembali dari kekacauan sebelumnya.
Untuk mempertimbangkan tampilan siklus dengan kelipatan periode 3 in $$$3,8 \ leqslant r \ leqslant $ 3,$ lakukan perubahan pada program sebelumnya:


Hasil dari program:



Siklus periode 3 muncul di sekitar titik r = 3,83 , dan kemudian dibagi secara berurutan menjadi siklus 6,12,24. Adanya siklus dengan periode 3 menyiratkan adanya siklus dari periode terbatas lainnya, serta siklus kacau tanpa periode sama sekali.

Diagram cabang memungkinkan Anda untuk mengikuti pengembangan sistem dengan perubahan parameter yang mulus. Dengan nilai tetap dari parameter, diagram laba-laba (diagram kamera) memungkinkan pelacakan titik-titik yang mengorbit.

Konstruksi diagram laba-laba memungkinkan Anda mengidentifikasi berbagai efek yang tidak terlihat pada diagram cabang. Mari kita menulis sebuah program:


Diagram kamera:

Penggandaan periode dalam sistem mekanis

Pertimbangkan persamaan diferensial yang memodelkan getaran teredam bebas dari titik material dari massa tertentu pada pegas non-linear, di mana redaman ditentukan oleh kecepatan.

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$ (6)

Dalam persamaan (6), istilah kx mewakili gaya pegas linier yang diterapkan pada titik material dari massa yang diberikan, dan istilah tersebut $$$\ beta x ^ {3}$ mewakili nonlinieritas aktual pegas.

Jika gaya bekerja pada sistem osilasi bebas (6), maka perpindahan titik material massa yang digunakan gaya ini dijelaskan oleh persamaan diferensial Duffing untuk osilasi paksa:

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$ (7)

Persamaan (7) untuk sebagian besar parameter yang termasuk di dalamnya diselesaikan secara numerik. Sistem mekanik untuk model matematika menurut persamaan (7) ditunjukkan pada gambar:



Fitur dari sistem yang diberikan adalah bahwa alih-alih pegas digunakan benang logam fleksibel, yang berosilasi dalam bidang vertikal, yang konstanta Hook k negatif. Dalam skema ini, titik-titik keseimbangan stabil (a) dan (c), dan titik keseimbangan tidak stabil (b).

Ketika suatu titik material dipindahkan dari posisi (b), gaya yang bekerja di atasnya adalah menjijikkan. Jika gaya periodik, misalnya, diciptakan oleh medan magnet osilasi sebagian teredam oleh hambatan udara. Kemudian, persamaan (7) adalah model matematika yang dapat diterima untuk perpindahan horisontal x (t) dari titik material dengan rentang parameter berikut $$$k <0, c> 0, \ beta> 0$ .

Untuk mempelajari perilaku sistem nonlinear seperti itu, kami ambil $$$k = -1, m = c = \ beta = \ omega = 1$ maka persamaan diferensial (7) berbentuk:

$$$x ^ {''} + x ^ {'} - x + x ^ {3} = F_ {0} cos (t)$ , (8)

Kami menulis sebuah program untuk integrasi numerik persamaan (8) di bawah kondisi awal $$$x (0) = 1, x ^ {'} (0) = 0$ di lapangan $$$100 \ leqslant t \ leqslant $ 20$ dan untuk masing-masing nilai amplitudo berikut $$$F_ {0} = 0,6; 0,7; 0,75; 0,8$ , dan dalam setiap kasus, plot solusi untuk pesawat $$$x (t), x ^ {'} (t)$ dan $$$t, x (t)$ :


Bagan sebagai hasil dari program





Transisi ini dari periode penggandaan ke kekacauan menunjukkan perilaku umum sistem mekanis nonlinear sebagai respons terhadap perubahan dalam parameter fisik yang sesuai, misalnya: $$$k, m, c, \ beta, \ omega, F_ {0}$ . Fenomena seperti itu tidak terjadi dalam sistem mekanis linier.

Penarik Lorenz

Substitusi ke dalam persamaan Duffing untuk osilasi paksa (7) mengarah ke sistem persamaan diferensial diferensial nonlinier, yang ditunjukkan dalam daftar sebelumnya. Sistem persamaan diferensial diferensial tiga dimensi yang diterapkan pada masalah meteorologi dipertimbangkan oleh E.N. Lorenz:

$$$\ frac {dx} {dt} = - sx + sy,$
$$$\ frac {dy} {dt} = - xz + rx-y,$ (9)
$$$\ frac {dz} {dt} = xy-dz$

Solusi untuk sistem (9) paling baik dilihat dalam proyeksi ke salah satu dari tiga pesawat. Kami menulis sebuah program integrasi numerik untuk nilai-nilai parameter b = \ frac {8} {3}, s = 10, r = 28 dan kondisi awal x (0) = - 8, y (0) = 8, z (0) = 27 :


Hasil dari program:



Mempertimbangkan gambar pada grafik dari waktu ke waktu, dapat diasumsikan bahwa titik P (x (t), y (t), z (t)) membuat jumlah acak dari osilasi, kanan atau kiri. Untuk aplikasi meteorologi sistem Lorenz, setelah sejumlah hari cerah yang acak, sejumlah hari hujan secara acak akan menyusul.

Pertimbangkan program untuk memetakan penarik Lorentz di bidang xyz untuk kondisi awal yang sedikit berbeda:


Hasil program ditunjukkan dalam grafik berikut:





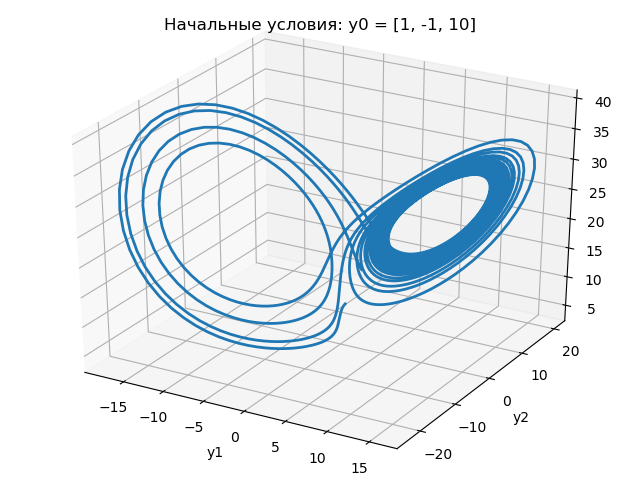
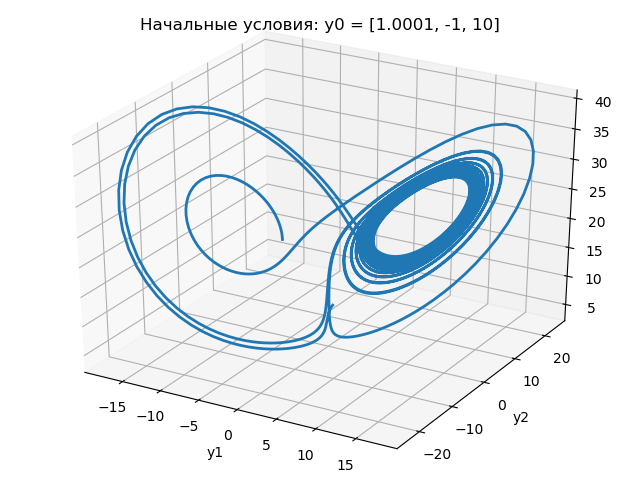
Dari grafik di atas dapat disimpulkan bahwa perubahan dalam kondisi awal dari 1,0 ke 1.0001 secara dramatis mengubah sifat perubahan pada penarik Lorentz.

Sistem Rossler

Ini adalah sistem tiga dimensi nonlinier yang dipelajari secara sangat intensif:
$$$\ frac {dx} {dt} = - y-z,$
$$$\ frac {dy} {dt} = x- \ alpha y,$ (10)
$$$\ frac {dz} {dt} = b + x (x-c).$

Kami akan menulis sebuah program untuk integrasi numerik sistem (10) untuk parameter berikut a = 0,39, b = 2, c = 4 dalam kondisi awal x (0) = 0, y (0) = 0, z (0) = 0 :


Hasil dari program:



Di pesawat, rekaman Rossler terlihat seperti lingkaran, tetapi di ruang angkasa ternyata diputar seperti pita Moebius.

Kesimpulan

Untuk menunjukkan fenomena kekacauan, disajikan program sederhana dan intuitif dalam bahasa pemrograman Python tingkat tinggi, yang mudah untuk ditingkatkan ke proyek baru pada topik ini. Artikel ini memiliki fokus pendidikan dan metodologi dan dapat digunakan dalam proses pembelajaran.

Referensi

1. Sedikit tentang kekacauan dan cara membuatnya
2. Pandangan kritis pada penarik Lorenz
3. FPGA Chaos Generator
4. Persamaan diferensial dan masalah nilai batas: pemodelan dan perhitungan menggunakan Mathematica, Maple dan MATLAB. Edisi ke-3: Per. dari bahasa inggris - M.: LLC “Saya. Williams, 2008. - 1104 p .: Ill. - Paral. dada. Bahasa inggris