Baru-baru ini,
materi diterbitkan di majalah Quanta, di mana penulis berbicara tentang sebuah fenomena yang mengejutkan dari sudut pandang pembaca yang tidak berpengalaman, dibuktikan oleh ahli matematika. Esensinya adalah bahwa hampir semua polinomial dari jenis tertentu tidak dapat direduksi, yaitu, mereka tidak dapat terurai. Bukti ini diterapkan di banyak bidang matematika murni. Tapi ini juga kabar baik bagi salah satu pilar kehidupan modern - enkripsi digital.
Untuk penyimpanan informasi digital yang andal, enkripsi menggunakan algoritma RSA banyak digunakan. Ini adalah versi yang dipompa dari skema yang bahkan dapat dihasilkan oleh siswa kelas tujuh untuk bertukar pesan dengan teman-teman: setiap huruf diberi nomor, yang dikalikan dengan kunci rahasia yang telah disepakati sebelumnya. Untuk mendekripsi pesan, cukup membaginya menjadi kunci rahasia.
Enkripsi RSA bekerja dengan cara yang serupa. Kami memberikan penjelasan yang sangat sederhana. Pengguna muncul dengan pesan dan melakukan operasi matematika tertentu di atasnya, termasuk mengalikan dengan jumlah yang sangat besar (panjang beberapa ratus digit). Satu-satunya cara untuk mendekripsi pesan adalah dengan menemukan faktor-faktor sederhana dari hasil *.
*Faktor utama suatu angka adalah bilangan prima yang perlu dikalikan untuk mendapatkan nomor tersebut. Jadi, untuk angka 12 itu 2 * 2 * 3, dan untuk angka 495 adalah 3, 3, 5 dan 11.
Keamanan enkripsi RSA didasarkan pada kenyataan bahwa matematika tidak tahu cara cepat untuk menemukan faktor prima dari angka yang sangat besar. Dan jika pesan terenkripsi tidak ditujukan untuk Anda, dan Anda tidak memiliki kunci untuk mendekripsi, maka upaya untuk menemukan kunci ini dapat memakan waktu ribuan tahun. Selain itu, ini juga berlaku untuk komputer paling modern, dengan bantuan yang masih tidak mungkin untuk memilih faktor sederhana yang benar.
Tapi ada solusinya.
Setiap angka dapat direpresentasikan sebagai persamaan aljabar unik. Dan, tidak seperti pencarian faktor prima dari suatu bilangan, pencarian faktor prima dari suatu polinom jauh lebih mudah. Dan begitu polinomial didekomposisi menjadi faktor prima seperti itu, informasi ini dapat digunakan untuk mencari faktor prima dari bilangan asli.
Begini cara kerjanya.
Langkah Satu: Pilih nomor apa saja yang faktor utamanya perlu Anda ketahui. Untuk mempermudah, ambil nomor 15.
Langkah Dua: 15 diterjemahkan menjadi biner:
1111.
Langkah Tiga: Ekspresi biner ini berubah menjadi polinomial dengan menerjemahkan semua bilangan biner menjadi koefisien polinomial:
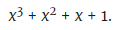
(Catatan: polinomial ini 15 jika x = 2. Angka 2 adalah basis dari sistem biner.)
Langkah keempat: Polinomial difaktorkan:
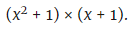Langkah Lima: x = 2 disubstitusi ke dalam masing-masing faktor ini:
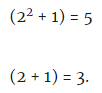Kesimpulan: 5 dan 3 adalah faktor utama dari 15.
Ya, ini adalah cara yang terlalu rumit untuk menemukan faktor-faktor sederhana dari sejumlah kecil seperti 15, yang mudah untuk dipikirkan. Namun, ketika datang ke jumlah besar yang terdiri dari ratusan angka, metode polinomial ini menawarkan keuntungan luar biasa. Untuk menguraikan bilangan prima, algoritma cepat tidak ada. Tetapi ada algoritma seperti itu untuk mendekomposisi polinomial besar. Karenanya, segera setelah Anda berhasil mengubah angka besar menjadi polinomial besar, Anda bisa sangat dekat dengan menemukan faktor-faktor sederhana dari angka tersebut.
Apakah ini berarti enkripsi RSA berisiko? Tidak juga. Dan pola baru, yang baru-baru ini terbukti mengenai polinomial, pasti terhubung dengan ini.
Matematikawan
Emmanuel Brulya dan
Peter Varju dari University of Cambridge membuktikan bahwa sebagai polinomial dengan koefisien 0 dan 1 menjadi lebih lama, probabilitas bahwa mereka dapat diperluas sama sekali menjadi lebih rendah. Dan jika polinomial tidak dapat diuraikan, maka itu tidak dapat digunakan untuk mencari faktor-faktor sederhana dari angka yang perlu dihitung.
Bukti Brull dan Varju sebenarnya menunjukkan bahwa solusi untuk memecahkan enkripsi RSA tidak mengarah ke mana pun. Angka yang sangat besar yang digunakan dalam RSA sesuai dengan polinomial yang sangat panjang. Ilmuwan Cambridge berpendapat bahwa hampir tidak mungkin menemukan polinomial dengan panjang seperti ini yang dapat terurai. Baik kriptografer dan matematikawan telah lama menduga bahwa ini benar. Namun, ketika keamanan dunia maya bergantung pada ketidakmungkinan menggunakan beberapa teknik matematika, selalu baik untuk memiliki bukti bahwa teknik ini tidak benar-benar berfungsi.
