Biquaternions

Jika Anda membuka artikel ini, Anda mungkin sudah pernah mendengar tentang angka empat, dan mungkin bahkan menggunakannya dalam desain Anda. Tapi sekarang saatnya untuk naik ke level yang lebih tinggi - ke biquaternions.

Artikel ini memberikan konsep dasar tentang biquaternions dan operasi dengannya. Untuk pemahaman yang lebih baik tentang bekerja dengan biquaternions, contoh yang jelas dalam Javascript menggunakan Kanvas ditampilkan.

Biquaternion

Biquaternion adalah angka hiperkompleks yang memiliki dimensi 8. Dalam artikel dan literatur berbahasa Inggris, mereka disebut "angka empat ganda," dan dalam literatur berbahasa Rusia ada juga nama "angka empat ganda" atau "angka empat kompleks".

Perbedaan utama dari angka empat adalah bahwa angka empat menggambarkan orientasi objek di ruang, dan biquaternion juga menggambarkan posisi objek di ruang.

Biquaternion dapat direpresentasikan sebagai dua angka empat:

$$

$$\ widetilde {\ textbf {q}} = \ begin {bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix},$$

$$$\ textbf {q} _1$ - bagian nyata, menentukan orientasi objek di ruang angkasa;
$$$\ textbf {q} _2$ - bagian ganda, menentukan posisi objek dalam ruang.

Biquaternion juga disebut sebagai quaternion kompleks, dalam hal ini diwakili sebagai quaternion, masing-masing komponen yang merupakan bilangan ganda (tidak harus bingung dengan kompleks). Nomor ganda $$$A = a_1 + \ epsilon a_2$ dimana $$$a_1$ dan $$$a_2$ Apakah bilangan real, dan $$$\ epsilon$ - Simbol Clifford (kompleksitas), memiliki properti $$$\ epsilon ^ 2 = 0$ . Kami tidak akan mempelajari matematika, karena kami lebih tertarik pada bagian terapan, oleh karena itu, lebih lanjut kami akan mempertimbangkan biquaternion sebagai dua angka empat.

Interpretasi geometris dari biquaternion

Dengan analogi dengan angka empat, dengan mana Anda dapat mengatur orientasi objek, biquaternion juga dapat mengatur posisi. Yaitu Biquaternion menetapkan dua nilai sekaligus - posisi dan orientasi objek dalam ruang. Jika kita mempertimbangkannya dalam dinamika, maka biquaternion mendefinisikan dua kuantitas - kecepatan gerak linier dan kecepatan sudut rotasi objek. Gambar di bawah ini menunjukkan arti geometris dari biquaternion.



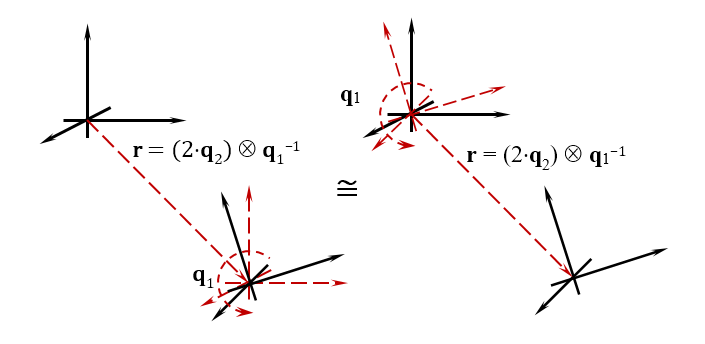
Pengembang game tahu bahwa untuk menentukan posisi dan orientasi suatu objek di ruang game, matriks rotasi dan matriks perpindahan digunakan, dan, tergantung pada urutan penerapannya, hasil dari posisi akhir objek berbeda. Bagi mereka yang terbiasa membagi gerakan menjadi operasi terpisah, terima aturan untuk bekerja dengan biquaternions: pertama-tama kita memindahkan objek, lalu kita memutarnya. Faktanya, Anda menggambarkan dua gerakan ini dengan satu angka, meskipun hypercomplex yang kompleks.

Karakteristik skalar

Pertimbangkan karakteristik skalar utama. Di sini perlu untuk memperhatikan fakta bahwa mereka mengembalikan bukan bilangan real biasa, tetapi dua.

1. Norma biquaternion

$$

$$\ | \ widetilde {\ textbf {q}} \ | = \ | \ textbf {q} _1 \ | + \ epsilon (q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2)$$

2. Modul Biquaternion

$$

$$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1 |}$$

Operasi dasar

Pertimbangkan operasi dasar bekerja dengan biquaternions. Seperti yang Anda lihat, mereka sangat mirip dengan operasi serupa dengan angka empat.

1. Pasangan Biquaternion

$$

$$\ widetilde {\ textbf {q}} ^ * = \ begin {bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$$

2. Penambahan dan pengurangan Biquaternion

$$

$$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ pm \ textbf {p} _2 \ end {bmatrix}$$

Penambahan dan pengurangan biquaternions bersifat komutatif (istilah dapat dipertukarkan).

3. Perkalian bilangan real dengan biquaternion

$$

$$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ begin {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$$

4. Multiplikasi Biquaternion

$$

$$\ widetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ otimes \ textbf {p} _1 \\ \ textbf {q} _1 \ otimes \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$$

Perkalian biquaternion adalah non-komutatif (dengan perubahan urutan faktor, hasil dari perkalian biquaternion berbeda).

Operasi ini adalah salah satu yang utama ketika bekerja dengan biquaternions dan membawa makna fisik, yaitu, hasil dari perkalian biquaternion adalah operasi penambahan rotasi dan gerakan linear dari dua biquaternions.

5. Membalik biquaternion

$$

$$\ widetilde {\ textbf {q}} ^ {- 1} = \ frac {\ widetilde {\ textbf {q}} ^ *} {\ | \ widetilde {\ textbf {q}} \ |}$$

Penentuan biquaternion melalui sudut orientasi dan vektor posisi

Pertama, kita mendefinisikan sistem koordinat di mana kita akan mempertimbangkan orientasi dan posisi objek di ruang angkasa. Ini harus dilakukan untuk menentukan bagian nyata dari biquaternion (orientasi angka empat), urutan rotasi yang mempengaruhi angka empat yang dihasilkan dari sudut orientasi. Di sini kita akan dipandu oleh sudut-sudut pesawat - yaw $$$\ psi$ melenggang $$$\ vartheta$ dan berguling $$$\ gamma$ .

Tentukan sistem koordinat dasar. Bayangkan Anda berdiri di permukaan Bumi dan melihat ke arah Utara.

Titik O _o - asal dari sistem koordinat, yang terletak di titik asal objek.
Sumbu O _o Yg - diarahkan secara vertikal ke atas, dan berlawanan dengan arah vektor gravitasi.
Sumbu O _oXg - diarahkan ke Utara, di sepanjang garis singgung meridian lokal.
Axis O _o Zg - melengkapi sistem ke kanan dan diarahkan ke kanan, ke arah Timur.

Sistem koordinat kedua terhubung. Bayangkan, misalnya, pesawat terbang atau benda lain.
Titik O - asal sistem koordinat, sebagai aturan, terletak di titik pusat massa objek.
Sumbu OY - diarahkan secara vertikal ke atas, dan tegak lurus terhadap bidang horizontal objek.
Axis OX - diarahkan maju ke titik depan objek.
Sumbu OZ - melengkapi sistem ke kanan.

Posisi objek dalam ruang ditentukan oleh radius vektor asal (titik O ) dari sistem koordinat terkait relatif terhadap sistem koordinat basis tetap. Orientasi sistem koordinat terkait relatif terhadap basis ditentukan oleh tiga putaran berturut-turut:

sudut menganga $$$\ psi$ - Rotasi di sekitar sumbu OY ,
sudut pitch $$$\ vartheta$ - Rotasi di sekitar sumbu OZ ,
sudut gulungan $$$\ gamma$ - Rotasi di sekitar sumbu OX .

Untuk penentuan awal biquaternion, Anda harus menentukan bagian nyata dan ganda biquaternion. Orientasi dan posisi objek diatur relatif ke sistem koordinat basis tertentu menggunakan sudut orientasi $$$\ psi, \ vartheta, \ gamma$ dan vektor posisi pusat massa $$$r = (r_x, r_y, r_z) ^ T$ .

Bagian yang sebenarnya $$$\ textbf {q} _1$ dapat diatur menggunakan rumus:

$$

$$\ textbf {q} _1 = \ begin {bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ cos \ frac { \ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ & sin \ frac {\ psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \ end {bmatrix}$$

Harap perhatikan bahwa jika Anda memiliki urutan rotasi yang berbeda, maka ekspresi juga akan berbeda.

Bagian ganda $$$\ textbf {q} _2$ didefinisikan oleh ungkapan:

$$

$$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$$

Perhitungan sudut orientasi dan vektor posisi dari biquaternion. Transformasi terbalik

Sudut orientasi dapat dihitung dari bagian sebenarnya dari biquaternion $$$\ textbf {q} _1$ :

$$

$$\ psi = \ arctan {\ frac {2 (q_0 q_2 - q_1 q_3)} {q_0 ^ 2 + q_1 ^ 2 - q_2 ^ 2 - q_3 ^ 2}}$$

$$

$$\ vartheta = \ arcsin {(2 (q_1 q_2 + q_0 q_3))}$$

$$

$$\ gamma = \ arctan {\ frac {2 (q_0 q_1 - q_2 q_3)} {q_0 ^ 2 - q_1 ^ 2 + q_2 ^ 2 - q_3 ^ 2}}$$

Posisi objek ditentukan oleh ekspresi:

$$

$$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {- 1}$$

hasilnya adalah vektor dalam bentuk angka empat $$$\ textbf {r} = (0, r_x, r_y, r_z) ^ T$

Putar dan pindahkan biquaternion vektor

Salah satu sifat besar biquaternions adalah rotasi dan pergerakan vektor dari satu sistem koordinat ke yang lain. Biarkan O oX g Yg Zg menjadi sistem koordinat basis tetap, dan OXYZ menjadi sistem koordinat objek yang terhubung. Kemudian orientasi dan posisi objek relatif terhadap sistem koordinat dasar dapat ditentukan oleh biquaternion $$$\ widetilde {\ textbf {q}}$ . Jika suatu vektor ditentukan $$$\ textbf {r}$ dalam sistem koordinat yang terhubung, maka Anda bisa mendapatkan vektor $$$\ textbf {r} _0$ dalam sistem koordinat dasar menggunakan rumus:

$$

$$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {- 1}$$

dan kembali:

$$

$$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {- 1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}}$$

dimana $$$\ textbf {r}$ Apakah vektor dalam bentuk biquaternion, $$$\ textbf {r} = (1, 0, 0, 0, 0, 0, r_x, r_y, r_z)$

Perpustakaan JavaScript Biquaternion

Semua operasi di atas dengan biquaternions diimplementasikan di perpustakaan-javascript, tergantung pada tugas Anda, itu dapat diimplementasikan dalam bahasa pemrograman lain. Fungsi utama bekerja dengan biquaternions:

Fungsi	Deskripsi
DualQuaternion.dq	Badan Biquaternion sebagai array dari 8 angka
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)	Konstruktor yang mendefinisikan biquaternion dengan menentukan semua delapan angka
DualQuaternion.fromEulerVector(psi, theta, gamma, v)	Dapatkan biquaternion dengan mengatur orientasi objek dengan sudut Euler dan vektor posisi objek
DualQuaternion.getEulerVector()	Dapatkan sudut Euler dan vektor posisi dari biquaternion
DualQuaternion.getVector()	Dapatkan vektor posisi dari biquaternion
DualQuaternion.getReal()	Dapatkan bagian nyata dari biquaternion (menentukan orientasi objek dalam ruang)
DualQuaternion.getDual()	Dapatkan bagian ganda dari biquaternion (menentukan posisi objek dalam ruang)
DualQuaternion.norm()	Dapatkan norma biquaternion sebagai angka ganda
DualQuaternion.mod()	Dapatkan modul biquaternion sebagai nomor ganda
DualQuaternion.conjugate()	Dapatkan biquaternion terkonjugasi
DualQuaternion.inverse()	Dapatkan Biquaternion Terbalik
DualQuaternion.mul(DQ2)	Multiplikasi Biquaternion
DualQuaternion.toString()	Konversikan biquaternion menjadi string, misalnya, untuk output ke konsol debug

Contoh bekerja dengan biquaternions

Untuk pemahaman yang lebih baik tentang dasar-dasar penggunaan biquaternions sebagai contoh, pertimbangkan permainan kecil. Area persegi panjang diatur - peta. Sebuah kapal melayang di peta dengan pistol putar yang terpasang di peta. Di sini perlu untuk memperhitungkan bahwa untuk kapal, sistem koordinat dasar adalah sistem koordinat peta, dan untuk pistol, sistem koordinat dasar adalah kapal. Semua objek digambar dalam sistem koordinat peta dan di sini akan menarik untuk melihat bagaimana Anda dapat beralih dari sistem koordinat pistol ke sistem koordinat peta menggunakan properti multiplikasi biquaternion. Pergerakan kapal dikendalikan oleh tombol W, A, S, D. Arah pistol diatur oleh kursor mouse.



Kapal dan senapan dijelaskan oleh dua kelas: Ship dan Gun . Dalam konstruktor kelas kapal, bentuknya dalam bentuk titik biquaternion, orientasi awal dan posisi pada peta dalam bentuk this.dq_pos .

Peningkatan Biquaternion juga diberikan untuk kontrol kapal. Saat bergerak bolak-balik (tombol W, S), hanya bagian ganda dari biquaternion yang akan berubah, dan ketika mengontrol kanan-kiri (tombol A, D), bagian nyata dan ganda dari biquaternion akan berubah, yang menentukan sudut rotasi.

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); //   this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); //      this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; }; 

Di kelas itu sendiri, hanya ada satu fungsi untuk merender kapal Ship.draw() . Perhatikan penerapan operasi biquaternion untuk mengalikan setiap titik kapal dengan biquaternion dari posisi saat ini dan orientasi kapal.

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** *   */ 'draw': function() { //         v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } }; 

Dalam konstruktor kelas senjata, bentuknya dalam bentuk titik biquaternion ditentukan. Pistol akan ditampilkan sebagai garis. Orientasi awal dan posisi pada kapal diatur oleh this.dq_pos . Juga, pengikatan ke kapal tempat ia diinstal juga diatur. Pistol di kapal hanya bisa berputar, jadi penambahan biquaternion saat mengendalikan pistol hanya akan mengubah bagian sebenarnya dari biquaternion, yang menetapkan sudut rotasi. Dalam contoh ini, implement dipandu oleh kursor mouse, sehingga rotasi pistol akan terjadi secara instan.

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; //     this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); //   this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); //     this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; }; 

Di kelas senjata, hanya satu fungsi renderingnya Ship.draw() juga diimplementasikan. Pistol ditampilkan sebagai garis, yang ditetapkan oleh dua titik this.dq_backward dan this.dq_forward . Untuk menentukan koordinat titik-titik pistol, operasi multiplikasi biquaternion digunakan.

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** *   */ 'draw': function() { //     v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } }; 

Pemrosesan kontrol kapal dan senjata diterapkan melalui berbagai peristiwa. Empat variabel leftPressed, upPressed, rightPressed, downPressed , yang diproses dalam loop program utama, bertanggung jawab untuk menekan dan melepaskan kunci kontrol kapal.

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); //     function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } //  S } //     function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } //  S } 

Salah satu fungsi yang paling menarik, dari sudut pandang menggunakan operasi biquaternion, adalah untuk mengontrol pistol kapal ke arah penunjuk mouse. Pertama, koordinat penunjuk tetikus ditentukan dalam dq_mouse_pos . Kemudian, biquaternion dari posisi mouse relatif terhadap kapal dihitung menggunakan perkalian biquaternion. Biquaternion kapal diambil dari dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(Catatan: operasi multiplikasi biquaternion berurutan dibaca dari kanan ke kiri). Dan akhirnya, sudut antara vektor alat dan mouse ditentukan. Gun titik awal gun_1.dq_backward diberikan nilai yang diterima.

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; //           if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { //    dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); //      //  .       //     // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); //       q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } } 

Di bagian utama program, objek kapal dan senjata ship_1 dan gun_1 , informasi debugging ditampilkan, dan pemrosesan kontrol kapal dilakukan.

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); //   if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw(); 

Tautan ke arsip berisi kode lengkap perpustakaan untuk bekerja dengan angka empat dan dua kutip, skrip program itu sendiri, dan file index.html, yang dapat dibuka secara lokal di browser untuk menjalankan contoh di atas.

Contoh bekerja dengan biquaternions

Kesimpulan

Anda mungkin memiliki pertanyaan: mengapa menggunakan alat matematika yang begitu rumit ketika Anda bisa bertahan dengan alat standar untuk memindahkan dan memutar objek? Salah satu keuntungan utama adalah bahwa bentuk penulisan biquaternion lebih efisien secara komputasi, karena semua operasi dengan biquaternions setelah ekspresi diperluas adalah linier. Video ini, Geometric Skinning dengan Approximate Dual Quaternion Blending, menunjukkan betapa jauh lebih efisien perhitungan biquaternion daripada metode lain.

Saya terutama mengambil informasi tentang penggunaan biquaternion dari sumber-sumber bahasa Inggris.
Dari literatur domestik, saya dapat menyarankan dua buku:

1. Chelnokov Yuri Nikolaevich. Quaternion dan model biquaternion dan metode mekanika padat dan aplikasinya. Geometri dan kinematika gerak. - karya teoritis monumental.
2. Gordeev Vadim Nikolaevich. Kuarter dan biquaternion dengan aplikasi dalam geometri dan mekanika. - Ini ditulis dalam bahasa yang lebih dimengerti dan menunjukkan aplikasi dalam tugas membentuk struktur spasial melengkung.